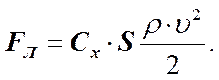Вязкость. Ламинарное и турбулентное течение жидкостей.

!!Вязкость — это способность жидкости сопротивляться сдвигу, т. е. свойство, обратное текучести (более вязкие жидкости являются менее текучими). Вязкость проявляется в возникновении касательных напряжений (напряжений трения). Рассмотрим слоистое течение жидкости вдоль стенки. В этом случае происходит торможение потока жидкости, обусловленное ее вязкостью. Причем скорость движения жидкости в слое тем ниже, чем ближе он расположен к стенке. Согласно гипотезе Ньютона касательное напряжение, возникающее в слое жидкости на расстоянии у от стенки, определяется зависимостью

 

где dυ/dy — градиент скорости, характеризующий интенсивность нарастания скорости υ при удалении от стенки (по оси у ).

Зависимость называют законом трения Ньютона. Течения большинства жидкостей, используемых в гидравлических системах, подчиняются закону трения Ньютона, и их называют ньютоновскими жидкостями. Однако следует иметь в виду, что существуют жидкости, в которых закон в той или иной степени нарушается. Такие жидкости называют неньютоновскими.

Величина μ получила название динамической вязкости жидкости. Она измеряется в Па*ּс либо в пуазах 1 Пз = 0.1 Па*ּс. Однако на практике более широкое применение нашла кинематическая вязкость:

Единицей измерения последней в системе СИ является м2/с или более мелкая единица см2/с, которую принято называть стоксом, 1 Ст = 1 см2/с. Для измерения вязкости также используются сантистоксы: 1 сСт = 0,01 Ст.

Вязкость жидкостей существенно зависит от температуры, причем вязкость капельных жидкостей с повышением температуры падает, а вязкость газов — растет (рисунок 1.4). Это объясняется тем, что в капельных жидкостях, где молекулы расположены близко друг к другу, вязкость обусловлена силами молекулярного сцепления. Эти силы с ростом температуры ослабевают, и вязкость падает. В газах молекулы располагаются значительно дальше друг от друга. Вязкость газа зависит от интенсивности хаотичного движения молекул. С ростом температуры эта интенсивность растет и вязкость газа увеличивается.

Вязкость жидкостей зависит также от давления, но это изменение незначительно, и в большинстве случаев его не учитывают.

Ламинарное течение

ламинарное течение характерезуется направлением водных (газовых) потоков. Они перемещаются слоями, не смешиваясь и без пульсаций. Другими словами, движение проходит равномерно, без беспорядочных скачков давления, направления и скорости. Ламинарное течение жидкости образуется, например, в узких кровеносных сосудах живых существ, капиллярах растений и в сопоставимых условиях, при течении очень вязких жидкостей (мазута по трубопроводу). Чтобы наглядно увидеть струйный поток, достаточно немного приоткрыть водопроводный кран – вода будет течь спокойно, равномерно, не смешиваясь. Если краник отвернуть до конца, давление в системе повысится и течение приобретет хаотичный характер.

Турбулентное течение

Турбулентное течение жидкости носит неупорядоченный характер. Если использовать подход Лагранжа, то траектории частиц могут произвольно пересекаться и вести себя достаточно непредсказуемо. Движения жидкостей и газов в этих условиях всегда нестационарные, причем параметры этих нестационарностей могут иметь весьма широкий диапазон.

Как ламинарный режим течения газа переходит в турбулентный, можно отследить на примере струйки дыма горящей сигареты в неподвижном воздухе. Вначале частицы движутся практически параллельно по неизменяемым во времени траекториям. Дым кажется неподвижным. Потом в каком-то месте вдруг возникают крупные вихри, которые движутся совершенно хаотически. Эти вихри распадаются на более мелкие, те – на еще более мелкие и так далее. В конце концов, дым практически смешивается с окружающим воздухом.

Циклы турбулентности

Вышеописанный пример является хрестоматийным, и из его наблюдения ученые сделали следующие выводы:

1. Ламинарное и турбулентное течение имеют вероятностный характер: переход от одного режима к другому происходит не в точно заданном месте, а в достаточно произвольном, случайном месте.

2. Сначала возникают крупные вихри, размер которых больше, чем размер струйки дыма. Движение становится нестационарным и сильно анизотропным. Крупные потоки теряют устойчивость и распадаются на все более мелкие. Таким образом, возникает целая иерархия вихрей. Энергия их движения передается от крупных к мелким, и в конце этого процесса исчезает – происходит диссипация энергии при мелких масштабах.

3. Турбулентный режим течения носит случайный характер: тот или иной вихрь может оказаться в совершенно произвольном, непредсказуемом месте.

4. Смешение дыма с окружающим воздухом практически не происходит при ламинарном режиме, а при турбулентном – носит очень интенсивный характер.

5. Турбулентность носит ярко выраженный нестационарный характер – все газодинамические параметры меняются во времени. Есть и еще одно важное свойство турбулентности: оно всегда трехмерно. Даже если рассматривать одномерное течение в трубе или двумерный пограничный слой, все равно движение турбулентных вихрей происходит в направлениях всех трех координатных осей.

Рейнольдс определил общие условия, при которых возможны существование ламинарного и турбулентного режима движения жидкости и переход от одного режима к другому. Оказалось, что состояние (режим) потока жидкости в трубе зависит от величины некоторого безразмерного числа, учитывающего основные факторы, определяющие это движение: среднюю скорость, диаметр трубы (или другие линейные характеристики потока), плотность жидкости и ее вязкость.

Влияние всех этих величин на характер движения жидкости объединены в формуле, выражающей число Рейнольдса:

Re = ρvR/µ,

где: R – гидравлический радиус потока; v – скорость потока; µ - динамическая вязкость жидкости, ρ – плотность жидкости.

Число Рейнольдса (иногда его называют критерием Рейнольдса) является безразмерной величиной. Поскольку динамическая вязкость жидкости связана с кинематической вязкостью соотношением µ = ρν, то критерий Рейнольдса можно записать в виде:

Re = vR/ν

Число Рейнольдса определяет границы, между которыми режим движения жидкости может принимать ламинарный или турбулентный характер.

 

!!32.Движение тел в жидкостях и газах. Лобовое сопротивление и подъемная сила

При движении тела в жидкости оно испытывает сопротивление движению. Сила, с которой жидкость действует на тело, в общем случае направлена под некоторым углом к направлению движения. Она создаётся двумя составляющими: одной, направленной вдоль потока F_Л, и вторая, перпендикулярная к ней F_П. Первая носит название лобового сопротивления, а вторая – подъёмной силы.

Воздействие потока жидкости на твёрдое тело зависит от относительной скорости движения тела и частиц жидкости, причём безразлично тело ли движется относительно покоящейся жидкости или неподвижное тело обтекает движущаяся жидкость. Если тело симметрично и его ось сим­метрии совпадает с направлением скоро­сти, то на него действует только лобовое сопротивление, подъемная же сила в этом случае равна нулю. Можно доказать, что в идеальной жидкости равномерное движение происходит без лобового сопро­тивления. Если рассмотреть движение ци­линдра в такой жидкости, то картина линий тока симметрична как от­носительно горизонтального, так и относительно вертикального направлений, т. е. ре­зультирующая сила давления на повер­хность цилиндра будет равна нулю.

Иначе обстоит дело при движении тел в вязкой жидкости (особенно при увеличе­нии скорости обтекания). Вследствие вяз­кости среды в области, прилегающей к по­верхности тела, образуется пограничный слой частиц, движущихся с меньшими ско­ростями. В результате тормозящего дейст­вия этого слоя возникает вращение частиц и движение жидкости в пограничном слое становится вихревым. Если тело не имеет обтекаемой формы (нет плавно утончаю­щейся хвостовой части), то пограничный слой жидкости отрывается от поверхности тела. За телом возникает течение жидко­сти (газа), направленное противоположно набегающему потоку. Оторвавшийся по граничный слой, следуя за этим течением, образует вихри, вращающиеся в противо­положные стороны

Лобовое сопротивление зависит от формы тела и его положения относительно потока, что учитывается безразмерным ко­эффициентом сопротивления С_x, определя­емым экспериментально:

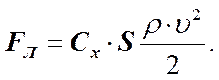
где ρ - плотность среды; υ - скорость движения тела; S - наибольшее попере­чное сечение тела.

Составляющую F_л можно значитель­но уменьшить, подобрав тело такой фор­мы, которая не способствует образованию завихрения.

Подъемная сила может быть определе­на аналогичной формулой:

где С_у - безразмерный коэффициент подъемной силы.

33. Гармонические колебания. Амплитуда, частота, фаза. Затухающие и вынужденные колебания.

 

Гармонические колебания - колебания, при которых физическая величина изменяется с течением времени по гармоническому (синусоидальному или косинусоидальному) закону.

X(t)=A sin(wt+f) X(t)=A cos(wt+f)

 

Амплитуда - максимальная величина смещения от положения равновесия (высота волны).

 

Частота колебаний - число полных колебаний в единицу времени.

 

Фаза колебаний - величина, которая определяет положение колебательной системы в любой момент времени.

Является аргументом функции (wt+f).

 

Затухающие колебания - колебания, энергия которых уменьшается с течением времени.

 

Вынужденные колебания- колебания, происходящие под воздействием внешних периодических сил.

Пример- качели.

 

 

34. Продольные и поперечные волны.

Волна - процесс распространения колебаний.

 

Поперечные волны- волны, перемещающиеся в направлении, перпендикулярном направлению распространения волны.

 

Продольные волны - волны, перемещающиеся в направлении, параллельном направлению распространению волны.

35. Газовые законы (Бойля-Мариотта, Гей-Люссака)

Закон Бойля-Мариотта- Для данной массы газа m при неизменной температуре Т произведение давления на объем есть величина постоянная: PV=const при T=const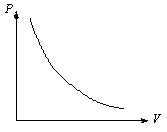

 

 

Закон Гей-Люссака- Для данной массы m при постоянном давлении р объем газа линейно зависит от температуры:

 

V/T=const при p=const

36. Модель идеального газа.

Идеальный газ - это физическая модель газа, взаимодействие между молекулами которого пренебрежительно мало.

- вводится для математического описания поведения газов. Реальные разреженные газы ведут себя как идеальный газ!

Свойства идеального газа:

- взаимодействие между молекулами пренебрежительно мало

- расстояние между молекулами много больше размеров молекул

- молекулы - это упругие шары

- отталкивание молекул возможно только при соударении

- движение молекул - по законам Ньютона

- давление газа на стенки сосуда - за счет ударов молекул газа