Траектория материальной точки. Путь и перемещение.

Физика. Экзамен

1.Кинематика. Понятие материальной точки (примеры).

Кинематика – раздел теоретической механики, в котором изучается механическое движение тел без учета их масс и причин, обеспечивающих это движение.

Иными словами, в кинематике описывается движение тела (траектория движения, скорость и ускорение) без выяснения причин, почему оно так движется.

Движением обозначают всякое изменение в окружающем материальном мире. Механическое движение – изменение положения тела в пространстве, прнноисходящее с течением времени, наблюдаемое относительно другого тела, условно принятого за неподвижное. Условно неподвижное тело называют телом отсчета. Система координатных осей, связанная с телом отсчета, определяет пространство, в котором происходит движение.

Основной единицей измерения расстояний служит 1 метр (м), единицей измерения углов – 1 радиан (рад.).

Время в кинематике рассматривается в качестве непрерывно изменяющейся скалярной величины t. Все другие кинематические величины считаются зависящими от времени (функциями от времени). За основную единицу времени принимают 1 сек.

Кинематика изучает движение:

· точки твердого (не поддающегося деформации) тела

· твердого тела, поддающегося упругой или пластической деформации

· жидкости

· газа

Основные задачи кинематики.

1. Описание движения тела с помощью кинематических уравнений движения, таблиц и графиков. Описать движение тела – определить его положение в любой момент времени.

2. Определение кинематических характеристик движения – скорости и ускорения.

3. Изучение сложных (составных) движений и определение зависимости между их характеристиками. Сложным движением называют движение тела относительно системы координат, которая сама движется относительно другой, неподвижной системы координат.

Кинематика рассматривает следующие понятия и движения:

· прямолинейное движение,

· относительность движения,

· равномерное движение по окружности,

· система отсчета,

· поступательное движение,

· материальная точка,

· траектория,

· задание положения точки,

· движение точки,

· перемещение и путь,

· скорость,

· механическое движение,

· относительная скорость,

· сложение скоростей,

· равномерное движение,

· ускорение,

· равнопеременное движение,

· угловая скорость,

· вращательное движение.

Материальной точкой называется тело, размерами которого в данных условиях можно пренебречь. Слово «материальная» подчеркивает здесь отличие этой точки от геометрической. Геометрическая точка не обладает никакими физическими свойствами. Материальная точка может обладать массой, электрическим зарядом и другими физическими характеристиками.

Одно и то же тело в одних условиях можно считать материальной точкой, а в других – нет. Так, например, рассматривая движение корабля из одного морского порта в другой, корабль можно считать материальной точкой. Однако, при исследовании движения шарика, который катится по палубе корабля, корабль считать материальной точкой нельзя. Движение зайца, убегающего по лесу от волка, можно описывать, приняв зайца за материальную точку. Но нельзя считать зайца материальной точкой, описывая его попытки спрятаться в нору. При изучении движения планет вокруг Солнца их можно описывать материальными точками, а при суточном вращении планет вокруг своей оси такая модель неприменима.

Важно понимать, что в природе материальных точек не существует. Материальная точка – это абстракция, модель для описания движения.

 

2.Система отсчета. Инерциальные и неинерциальные системы отсчета (примеры).

Системой отсчета в физике называют совокупность тела отсчета, системы координат, связанной с телом отсчета, и часы или иной прибор для отсчета времени. При этом всегда следует помнить, что всякая система отсчета условна и относительна. Всегда можно принять другую систему отсчета, относительно которой любое движение будет иметь совершенно другие характеристики.

Телом отсчета называют тело, по отношению к которому рассматривают изменение положения других тел в пространстве.

С телом отсчета связывается система координат, которая представляет из себя точку отсчета. Для определения положения тела в пространстве в любой момент времени необходимо задать начало отсчета времени.

Инерциальная система отсчёта (ИСО) — система отсчёта, в которой все свободные тела движутся прямолинейно и равномерно, либо покоятся.

Если не учитывать центростремительное ускорение Земли, то Землю можно назвать инерциальной системой отсчета. Поезд, который движется прямолинейно и равномерно - тоже инерциальная система отсчета.

Неинерциальная система отсчёта (НСО) – система отсчёта, движущаяся с ускорением или поворачивающаяся относительно инерциальной. Для того чтобы уравнение движения материальной точки в неинерциальной системе отсчёта по форме совпадало с уравнением второго закона Ньютона, дополнительно к «обычным» силам, действующим в инерциальных системах, вводят силы инерции.

Все реальные системы отсчёта неинерциальные. Законы Ньютона выполняются лишь в инерциальных системах отсчёта.

В НСО тело движется с ускорением и в тех случаях, когда на него внешние силы не действуют.

Например, если автобус движется с ускорением относительно Земли, то в системе отсчета, связанной с автобусом, на все тела будет действовать сила инерции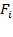

 

Угловое ускорение.

Для характеристики неравномерного вращения тела вводится понятие углового ускорения. Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

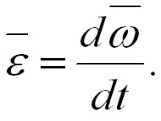
При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора угловой скорости (рис. 1.7); при ускоренном движении вектор ε направлен в ту же сторону, что и ω (dω/dt > 0), и в противоположную сторону при замедленном вращении (dω/dt < 0).

Первый закон Ньютона.

Он также известен как Закон инерции. Инерция — это свойство тела сохранять скорость своего движения неизменной (и по величине, и по направлению), когда на тело не действуют никакие силы.

В современной формулировке: Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения.

В исторической формулировке: Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

Второй закон Ньютона

Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся ускорением этой точки. Второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта.

Масса материальной точки при этом полагается величиной постоянной во времени и независящей от каких-либо особенностей её движения и взаимодействия с другими телами.

Современная формулировка: В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.

1 Н (ньютон) – сила, которая массе 1 кг сообщает ускорение 1 м/с² в направлении действия силы:

1 Н = 1 кг*м/с²

Третий закон Ньютона

Два тела действуют друг на друга с силами, равными по модулю и противоположными по направлению. Эти силы имеют одну и ту же физическую природу и направлены вдоль прямой, соединяющей их точки приложения.

Например, книга, лежащая на столе, действует на стол с силой, прямо пропорциональной своей массе и направленной вертикально вниз. Согласно третьему закону Ньютона стол в это же время действует на книгу с абсолютно такой же по величине силой, но направленной не вниз, а вверх.

 

 

Гравитационная сила

В 1687 г. Ньютон установил один из фундаментальных законов механики, получивший название закона всемирного тяготения: любые две материальные частицы притягиваются друг к другу с силой, пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.
Эту силу называют силой тяготения (или гравитационной силой).

Гравитационная постоянная

Из предыдущей формулы при m₁=m₂=m имеем

G=Fr²/m².

Из этой формулы видно, что гравитационная постоянная численно равна силе взаимного тяготения двух материальных точек, имеющих массы, равные единице массы, и находящихся друг от друга на расстоянии, равном единице длины.
Числовое значение гравитационной постоянной устанавливают экспериментально. Впервые это сделал английский ученый Кэвендиш с помощью крутильного динамометра (крутильных весов).

В СИ гравитационная постоянная имеет значение

G = 6,67·10^-11 Нм²/кг².

Следовательно, две материальные точки массой 1 кг каждая, находящиеся друг от друга на расстоянии 1 м, взаимно притягиваются гравитационной силой, равной 6,67·10^-11 Н.

Однородная сила тяжести — сила, действующая на любое материальное тело, находящееся вблизи поверхности Земли или другого астрономического тела. По определению, сила тяжести на поверхности планеты складывается из гравитационного притяжения планеты и центробежной силы инерции, вызванной суточным вращением планеты. Ускорение, сообщаемое телу силой тяжести, называется ускорением свободного падения.

F = m g,

где m – масса тела; g – ускорение свободного падения, g = 9.8 м/с².

где М - масса Земли; R - радиус Земли.

F_т + F_уп=mа

Где F_уп - сила упругости

 

24.Кинетическая и потенциальная энергия (примеры).

Кинетическая энергия Т механической системы – мера механического движения тела, зависящая от скорости движения в данной инерциальной системе отсчета. Тело массой m, движущейся со скоростью v, обладает кинетической энергией

Учитывая формулу p=mv, выражение для кинетической энергии можно записать в виде 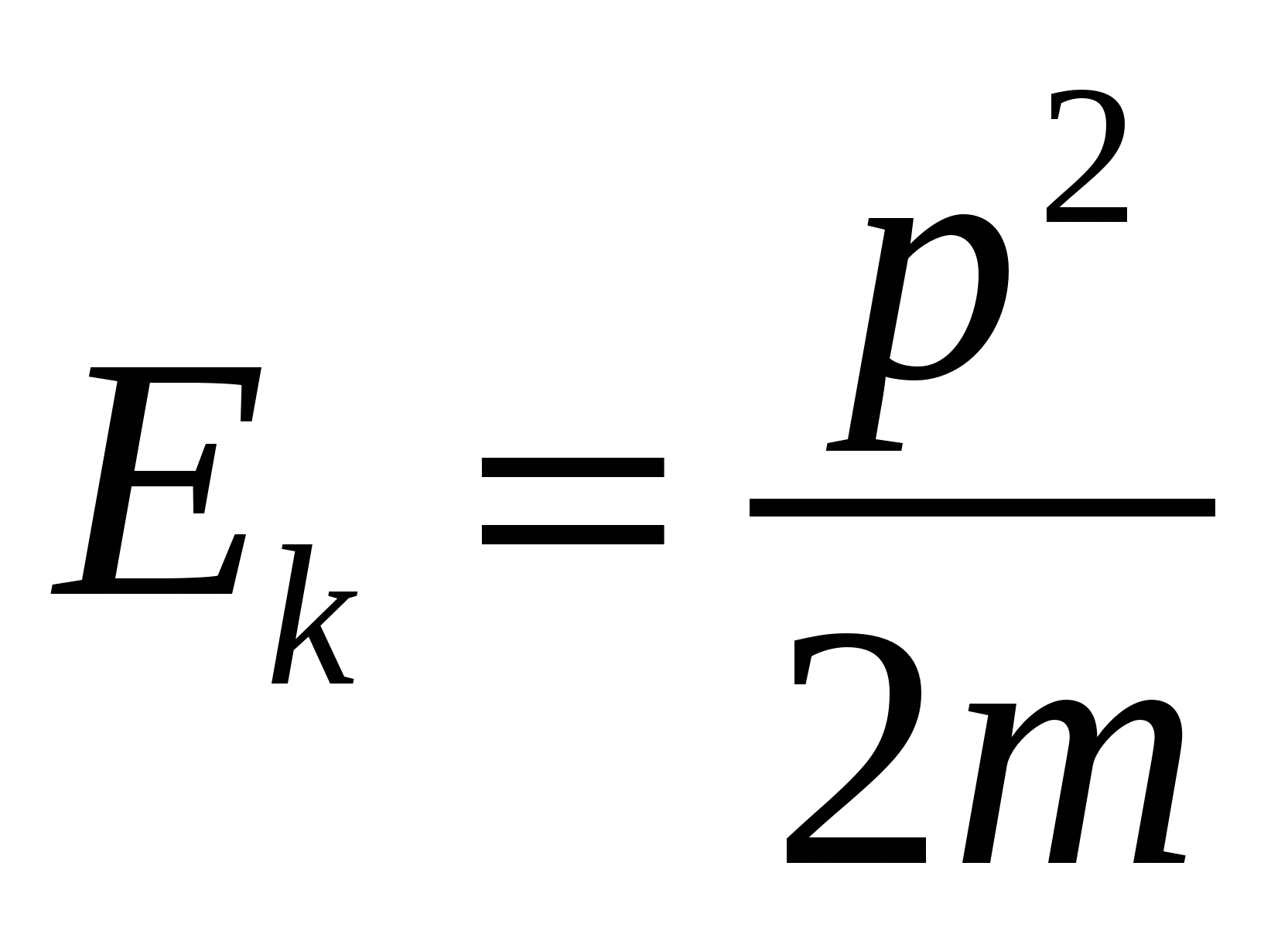р – импульс тела

Потенциальная энергия – это энергия, которая определяется взаимным расположением тел, а также характером сил взаимодействия между этими телами.

Она зависит от расстояния, на котором находятся тела, и не зависит от их скорости. Таким образом, потенциальная энергия - это скалярная величина, имеющая числовое значение, но не имеющая вектора направления. Также она способна совершать работу под действием сил поля.

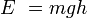
m - Масса тела.

g - Ускорение свободного падения.

h - Высота.

Еще одним примером консервативной силы можно считать силу упругой деформации. Скажем, к примеру, если взять пружину, на конце которой закреплен груз.

В начальном состоянии, когда пружине не растянута и не сжата груз обладает нулевой потенциальной энергией. Если пружину сжать, то есть изменить положение тела. То груз приобретет некоторую энергию. Далее при отпускании потенциальная энергия перейдет в силу движения и вернет груз в начальное положение.

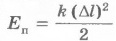
k - коэффициент упругости.

l - изменение длинны.

Примером потенциальной энергии можно считать, такую энергию которой обладает тело массой m подвешенное на некотором расстоянии от земли. В данном случае взаимодействуют два тела. Это земля и подвешенный груз. Роль потенциального поля сил играет гравитационное поле земли. Консервативная сила в данном случае это сила тяжести. Расстоянием между телами считается расстояние между грузом и поверхностью земли.

Полная механическая энергия тела или системы тел равна сумме кинетической и потенциальной энергий тела (системы тел):

Wполн. = W кин.+ Wпот

Пример: Мяч бросают с какой-то высоты на землю. В верхней точки он обладает потенциальной энергией, кинетическая равна нулю. С уменьшением высота эта энергия тоже уменьшается. Когда мяч упадет на землю, он покатится. Его потенциальная энергия станет равной нулю, а кинетическая примет какое-то значение.

Когда человек сидит на стуле, он обладает потенциальной энергией, т. е. возможностью что-то совершить. А бегущий человек обладает кинетической, энергией движущегося тела.

 

25.Закон сохранения энергии в механике.

Закон сохранения энергии: при любых процессах, происходящих в замкнутой консервативной системе, её полная механическая энергия не изменяется.

Е = Екин + Епот = const

здесь Е — полная механическая энергия. Полная механическая энергия остается постоянной:

Существует еще один вид систем – диссиативные системы, в которых механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы энергии. Этот процесс получил название дисспации (рассеяния) энергии.

Физическая сущность закона сохранения и превращения энергии заключается в том, что при любых физических взаимодействиях энергия не исчезает и не появляется вновь, она лишь превращается из одного вида в другой.

 

Уравнение неразрывности

Рассмотрим какую-либо трубку тока. Выберем два ее сечения S ₁ и S ₂, перпендикулярные направлению скорости (рис. 46).

За время D t через сечение S проходит объем жидкости Sv D t; следовательно, за 1 с через S ₁ пройдет объем жидкости S ₁ v ₁, где v ₁ — скорость течения жидкости в месте сечения S ₁. Через сечение S ₂ за 1 с пройдет объем жидкости S ₂ v ₂, где v ₂ — скорость течения жидкости в месте сечения S ₂. Здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость несжимаема (r=const), то через сечение S ₂ пройдет такой же объем жидкости, как и через сечение S ₁, т. е.

S₁v₁ = S ₂ v ₂=const

Следовательно, произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока. Это соотношение называется уравнением неразрывности для несжимаемой жидкости.

 

Уравнение Бернулли.

Уравнение Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

Для стабильно текущего потока (газа или жидкости) сумма кинетической и потенциальной энергии, давления на единицу объема является постоянной в любой точке этого потока.

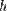— плотность жидкости, — скорость потока, — высота, на которой находится рассматриваемый элемент жидкости, — давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости, 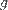— ускорение свободного падения.

Первое и второе слагаемое в Законе Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. А третье слагаемое в нашей формула является работой сил давления и не запасает какую-либо энергию. Из этого можно сделать вывод, что размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости или газа.

Постоянная в правой части уравнения Бернулли называется полным давлением и зависит в общих случаях, только от линии потока.

Если у вас горизонтальная труба, то Уравнение Бернулли принимает некий другой вид. Так как h=0, то потенциальная энергия будет равняться нулю, и тогда получится:

Из Уравнения Бернулли можно сделать вывод: при уменьшении сечения потока возрастает скорость движения газа или жидкости (возрастает динамическое давление ), но в этот же момент уменьшает статическое давление следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает.

Бернулли объединил законы механики Ньютона с законом сохранения энергии и условием неразрывности жидкости, и смог вывести уравнение (Уравнение Бернулли), согласно которому давление со стороны текучей среды (жидкость или газ) падает с увеличением скорости потока этой среды. В случае с самолетом воздух обтекает крыло самолета снизу медленнее, чем сверху. И благодаря этому эффекту обратной зависимости давления от скорости давление воздуха снизу, направленное вверх, оказывается больше давления сверху, направленного вниз. В результате, по мере набора самолетом скорости, возрастает направленная вверх разность давлений, и на крылья самолета действует нарастающая по мере разгона подъемная сила. Как только она начинает превышать силу гравитационного притяжения самолета к земле, самолет в буквальном смысле взмывает в небо. Эта же сила удерживает самолет в горизонтальном полете: на крейсерской скорости и высоте подъемная сила уравновешивает силу тяжести.

 

Ламинарное течение

ламинарное течение характерезуется направлением водных (газовых) потоков. Они перемещаются слоями, не смешиваясь и без пульсаций. Другими словами, движение проходит равномерно, без беспорядочных скачков давления, направления и скорости. Ламинарное течение жидкости образуется, например, в узких кровеносных сосудах живых существ, капиллярах растений и в сопоставимых условиях, при течении очень вязких жидкостей (мазута по трубопроводу). Чтобы наглядно увидеть струйный поток, достаточно немного приоткрыть водопроводный кран – вода будет течь спокойно, равномерно, не смешиваясь. Если краник отвернуть до конца, давление в системе повысится и течение приобретет хаотичный характер.

Турбулентное течение

Турбулентное течение жидкости носит неупорядоченный характер. Если использовать подход Лагранжа, то траектории частиц могут произвольно пересекаться и вести себя достаточно непредсказуемо. Движения жидкостей и газов в этих условиях всегда нестационарные, причем параметры этих нестационарностей могут иметь весьма широкий диапазон.

Как ламинарный режим течения газа переходит в турбулентный, можно отследить на примере струйки дыма горящей сигареты в неподвижном воздухе. Вначале частицы движутся практически параллельно по неизменяемым во времени траекториям. Дым кажется неподвижным. Потом в каком-то месте вдруг возникают крупные вихри, которые движутся совершенно хаотически. Эти вихри распадаются на более мелкие, те – на еще более мелкие и так далее. В конце концов, дым практически смешивается с окружающим воздухом.

Циклы турбулентности

Вышеописанный пример является хрестоматийным, и из его наблюдения ученые сделали следующие выводы:

1. Ламинарное и турбулентное течение имеют вероятностный характер: переход от одного режима к другому происходит не в точно заданном месте, а в достаточно произвольном, случайном месте.

2. Сначала возникают крупные вихри, размер которых больше, чем размер струйки дыма. Движение становится нестационарным и сильно анизотропным. Крупные потоки теряют устойчивость и распадаются на все более мелкие. Таким образом, возникает целая иерархия вихрей. Энергия их движения передается от крупных к мелким, и в конце этого процесса исчезает – происходит диссипация энергии при мелких масштабах.

3. Турбулентный режим течения носит случайный характер: тот или иной вихрь может оказаться в совершенно произвольном, непредсказуемом месте.

4. Смешение дыма с окружающим воздухом практически не происходит при ламинарном режиме, а при турбулентном – носит очень интенсивный характер.

5. Турбулентность носит ярко выраженный нестационарный характер – все газодинамические параметры меняются во времени. Есть и еще одно важное свойство турбулентности: оно всегда трехмерно. Даже если рассматривать одномерное течение в трубе или двумерный пограничный слой, все равно движение турбулентных вихрей происходит в направлениях всех трех координатных осей.

Рейнольдс определил общие условия, при которых возможны существование ламинарного и турбулентного режима движения жидкости и переход от одного режима к другому. Оказалось, что состояние (режим) потока жидкости в трубе зависит от величины некоторого безразмерного числа, учитывающего основные факторы, определяющие это движение: среднюю скорость, диаметр трубы (или другие линейные характеристики потока), плотность жидкости и ее вязкость.

Влияние всех этих величин на характер движения жидкости объединены в формуле, выражающей число Рейнольдса:

Re = ρvR/µ,

где: R – гидравлический радиус потока; v – скорость потока; µ - динамическая вязкость жидкости, ρ – плотность жидкости.

Число Рейнольдса (иногда его называют критерием Рейнольдса) является безразмерной величиной. Поскольку динамическая вязкость жидкости связана с кинематической вязкостью соотношением µ = ρν, то критерий Рейнольдса можно записать в виде:

Re = vR/ν

Число Рейнольдса определяет границы, между которыми режим движения жидкости может принимать ламинарный или турбулентный характер.

 

!!32.Движение тел в жидкостях и газах. Лобовое сопротивление и подъемная сила

При движении тела в жидкости оно испытывает сопротивление движению. Сила, с которой жидкость действует на тело, в общем случае направлена под некоторым углом к направлению движения. Она создаётся двумя составляющими: одной, направленной вдоль потока F_Л, и вторая, перпендикулярная к ней F_П. Первая носит название лобового сопротивления, а вторая – подъёмной силы.

Воздействие потока жидкости на твёрдое тело зависит от относительной скорости движения тела и частиц жидкости, причём безразлично тело ли движется относительно покоящейся жидкости или неподвижное тело обтекает движущаяся жидкость. Если тело симметрично и его ось сим­метрии совпадает с направлением скоро­сти, то на него действует только лобовое сопротивление, подъемная же сила в этом случае равна нулю. Можно доказать, что в идеальной жидкости равномерное движение происходит без лобового сопро­тивления. Если рассмотреть движение ци­линдра в такой жидкости, то картина линий тока симметрична как от­носительно горизонтального, так и относительно вертикального направлений, т. е. ре­зультирующая сила давления на повер­хность цилиндра будет равна нулю.

Иначе обстоит дело при движении тел в вязкой жидкости (особенно при увеличе­нии скорости обтекания). Вследствие вяз­кости среды в области, прилегающей к по­верхности тела, образуется пограничный слой частиц, движущихся с меньшими ско­ростями. В результате тормозящего дейст­вия этого слоя возникает вращение частиц и движение жидкости в пограничном слое становится вихревым. Если тело не имеет обтекаемой формы (нет плавно утончаю­щейся хвостовой части), то пограничный слой жидкости отрывается от поверхности тела. За телом возникает течение жидко­сти (газа), направленное противоположно набегающему потоку. Оторвавшийся по граничный слой, следуя за этим течением, образует вихри, вращающиеся в противо­положные стороны

Лобовое сопротивление зависит от формы тела и его положения относительно потока, что учитывается безразмерным ко­эффициентом сопротивления С_x, определя­емым экспериментально:

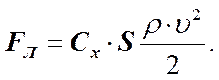
где ρ - плотность среды; υ - скорость движения тела; S - наибольшее попере­чное сечение тела.

Составляющую F_л можно значитель­но уменьшить, подобрав тело такой фор­мы, которая не способствует образованию завихрения.

Подъемная сила может быть определе­на аналогичной формулой:

где С_у - безразмерный коэффициент подъемной силы.

33. Гармонические колебания. Амплитуда, частота, фаза. Затухающие и вынужденные колебания.

 

Гармонические колебания - колебания, при которых физическая величина изменяется с течением времени по гармоническому (синусоидальному или косинусоидальному) закону.

X(t)=A sin(wt+f) X(t)=A cos(wt+f)

 

Амплитуда - максимальная величина смещения от положения равновесия (высота волны).

 

Частота колебаний - число полных колебаний в единицу времени.

 

Фаза колебаний - величина, которая определяет положение колебательной системы в любой момент времени.

Является аргументом функции (wt+f).

 

Затухающие колебания - колебания, энергия которых уменьшается с течением времени.

 

Вынужденные колебания- колебания, происходящие под воздействием внешних периодических сил.

Пример- качели.

 

 

34. Продольные и поперечные волны.

Волна - процесс распространения колебаний.

 

Поперечные волны- волны, перемещающиеся в направлении, перпендикулярном направлению распространения волны.

 

Продольные волны - волны, перемещающиеся в направлении, параллельном направлению распространению волны.

35. Газовые законы (Бойля-Мариотта, Гей-Люссака)

Закон Бойля-Мариотта- Для данной массы газа m при неизменной температуре Т произведение давления на объем есть величина постоянная: PV=const при T=const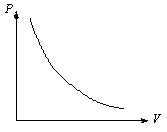

 

 

Закон Гей-Люссака- Для данной массы m при постоянном давлении р объем газа линейно зависит от температуры:

 

V/T=const при p=const

36. Модель идеального газа.

Идеальный газ - это физическая модель газа, взаимодействие между молекулами которого пренебрежительно мало.

- вводится для математического описания поведения газов. Реальные разреженные газы ведут себя как идеальный газ!

Свойства идеального газа:

- взаимодействие между молекулами пренебрежительно мало

- расстояние между молекулами много больше размеров молекул

- молекулы - это упругие шары

- отталкивание молекул возможно только при соударении

- движение молекул - по законам Ньютона

- давление газа на стенки сосуда - за счет ударов молекул газа

 

Подключение

Скорость света

скорость света в вакууме

Измерения скорости света в различных прозрачных веществах показали, что она всегда меньше, чем в вакууме. Например, в воде скорость света уменьшается в 4/3 раза.

Отношение скорости света в вакууме к скорости света в веществе называется абсолютным показателем преломления вещества.

При переходе световой волны из вакуума в вещество частота остается постоянной (цвет не изменяется). Длина волны в среде с показателем преломления n изменяется:

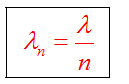
Законы теплового излучения.

Любое нагретое тело излучает электромагнитные волны. Чем выше температура тела, тем более короткие волны оно испускает. Тело, находящееся в термодинамическом равновесии со своим излучением, называют абсолютно черным (АЧТ). Излучение абсолютно черного тела зависит только от его температуры.

Закон Планка

Макс Планк вывел формулу, по которой при заданной температуре абсолютно черного тела можно рассчитать величину интенсивности его излучения:

-постоянная Планка = 1.054 · 10^-34 Дж·с

Закон Стефана–Больцмана

Стефаном и Больцманом был установлен закон, выражающий количественное соотношение между полной излучательной способностью и температурой черного тела:

Энергетическая светимость (q) абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры (T).

q = σ ⋅ T⁴

Константа в этой формуле называется постоянной Стефана-Болъцмана, σ = 5.67⋅10^-8 (Вт/м²)/К⁴.

Закон Вина

Длина волны (λмакс), на которую приходится максимум энергии в спектре равновесного излучения, обратно пропорциональна абсолютной температуре (Т) абсолютно черного тела.

Закон излучения Кирхгофа

Отношение излучательной способности (E) к поглощательной способности (A) одинаково для всех тел при данной температуре (T) для данной длины волны (λ) и не зависит от формы тела, его химического состава и проч.

E(λ,T) / A(λ,T) = e(λ,T)

По времени жизни

Все элементарные частицы делятся на два класса:

Стабильные элементарные частицы — частицы, имеющие бесконечно большое время жизни в свободном состоянии (протон, электрон, нейтрино, фотон, гравитон и их античастицы).

Нестабильные элементарные частицы — частицы, распадающиеся на другие частицы в свободном состоянии за конечное время (все остальные частицы).

По массе

Все элементарные частицы делятся на два класса:

Безмассовые частицы — частицы с нулевой массой (фотон, глюон, гравитон и их античастицы).

Частицы с ненулевой массой (все остальные частицы).

По величине спина

Все элементарные частицы делятся на два класса:

бозоны — частицы с целым спином (например, фотон, глюон, мезоны, бозон Хиггса);

фермионы — частицы с полуцелым спином (например, электрон, протон, нейтрон, нейтрино).

По видам взаимодействий

Элементарные частицы делятся на следующие группы:

Составные частицы

Адроны — частицы, участвующие во всех видах фундаментальных взаимодействий. Они состоят из кварков и подразделяются, в свою очередь, на:

мезоны — адроны с целым спином, то есть являющиеся бозонами;

барионы — адроны с полуцелым спином, то есть фермионы. К ним, в частности, относятся частицы, составляющие ядро атома, — протон и нейтрон.

Экспоненциальный закон

В указанном выше математическом выражении {\displaystyle \lambda } — постоянная распада, которая характеризует вероятность радиоактивного распада за единицу времени. Знак минус указывает на убыль числа радиоактивных ядер со временем.

Решение этого дифференциального уравнения имеет вид:

N(t)=

где {\displaystyle N_{0}} — начальное число атомов, то есть число атомов для {\displaystyle t=0.}

Таким образом, число радиоактивных атомов уменьшается со временем по экспоненциальному закону.

Активность радиоактивного препарата — число элементарных радиоактивных распадов в единицу времени

Удельная активность — активность, приходящаяся на единицу массы вещества препарата.

Объёмная активность — активность, приходящаяся на единицу объёма источника. Удельная и объёмная активности используются, как правило, в случае, когда радиоактивное вещество распределено по объёму препарата.

Поверхностная активность — активность, приходящаяся на единицу площади поверхности источника. Эта величина применяется для случаев, когда радиоактивное вещество распределено по поверхности препарата

Единица измерения- беккерель (Бк). (1 Бк=1 расп/с).

Гипотеза де Бройля.

Корпускулярно-волновой дуализм −− важнейшее универсальное свойство природы, заключающееся в том, что всем микрообъектам присущи одновременно и корпускулярные, и волновые характеристики.

Гипотеза де Бройля состоит в том, что если частица имеет энергию E и импульс p, то с этой частицей связана волна частотой

и длиной (длиной волны де Бройля)

Подуровни оболочек

Каждая оболочка состоит из одного или нескольких подуровней, каждый из которых состоит из атомных орбиталей.

 

К примеру, первая оболочка (K) состоит из одного подуровня «1s». Вторая оболочка (L) состоит из двух подуровней, 2s и 2p. Третья оболочка (M) — из «3s», «3p» и «3d». Четвертая (N) - из «4s», «4p», «4d», «4f».

Физика. Экзамен

1.Кинематика. Понятие материальной точки (примеры).

Кинематика – раздел теоретической механики, в котором изучается механическое движение тел без учета их масс и причин, обеспечивающих это движение.

Иными словами, в кинематике описывается движение тела (траектория движения, скорость и ускорение) без выяснения причин, почему оно так движется.

Движением обозначают всякое изменение в окружающем материальном мире. Механическое движение – изменение положения тела в пространстве, прнноисходящее с течением времени, наблюдаемое относительно другого тела, условно принятого за неподвижное. Условно неподвижное тело называют телом отсчета. Система координатных осей, связанная с телом отсчета, определяет пространство, в котором происходит движение.

Основной единицей измерения расстояний служит 1 метр (м), единицей измерения углов – 1 радиан (рад.).

Время в кинематике рассматривается в качестве непрерывно изменяющейся скалярной величины t. Все другие кинематические величины считаются зависящими от времени (функциями от времени). За основную единицу времени принимают 1 сек.

Кинематика изучает движение:

· точки твердого (не поддающегося деформации) тела

· твердого тела, поддающегося упругой или пластической деформации

· жидкости

· газа