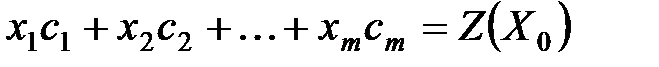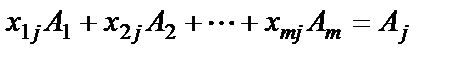Симплексный метод решения задачи линейного программирования

Построение опорных планов.Доказано, что оптимальное решение задачи линейного программирования связано с угловыми точками многогранника решений, т. е. с опорными планами, каждый из которых определяется системой m линейно независимых векторов, содержащихся в данной системе из n векторов А₁, А₂,..., А_n. Верхняя граница количества опорных планов, содержащихся в данной задаче, определяется числом сочетаний С_n^m. При больших m и n найти оптимальный план, перебирая все опорные планы задачи, очень трудно. Поэтому необходимо иметь схему, позволяющую осуществлять упорядоченный переход от одного опорного плана к другому. Такой схемой является симплексный метод, который позволяет, исходя из известного опорного плана задачи, за конечное число шагов получить ее оптимальный план. Каждый из шагов (или итераций) состоит в нахождении нового плана, которому соответствует меньшее значение линейной функции, чем значение этой же функции в предыдущем плане. Процесс продолжают до получения оптимального плана. Если задача не обладает планами или ее линейная функция не ограничена на многограннике решений, то симплексный метод позволяет установить это в процессе решения.

1. Построение опорных планов

Пусть поставлена задача линейного программирования.

Найти минимальное значение функции Z = C₁x₁ + C₂x₂ + … + C_nx_n при ограничениях:

где b_i і 0 (I=1,2,…,m).

Предположим сначала, что система ограничений задачи содержит m единичных векторов, причем без ограничения общности можно положить, что единичными являются первые m векторов. Тогда необходимо минимизировать линейную функцию

(1.11)

При ограничениях:

 

	(1.12)
	(1.13)

 

Запишем систему в векторной форме:

(1.14)

 

где

 

Векторы А₁, А₂, …, А_m – линейно независимые единичные векторы m-мерного пространства. Они и образуют базис этого пространства. Поэтому в разложении (1.14) за базисные неизвестные выбираем х₁, х₂,..., х_m, свободные неизвестные х_m+1,..., х_n приравниваем нулю и, учитывая, что b_i і 0 (i=1,2,…,m), а векторы А₁, А₂,..., А_m – единичные, получаем первоначальный план:

Плану соответствует разложение

(1.15)

где векторы А₁,А₂,…,А_m линейно независимы, следовательно, построенный первоначальный план является и опорным.

Рассмотрим, как, исходя из первоначального опорного плана, можно построить второй опорный план. Векторы А₁,А₂,…,А_m образуют базис в m-мерном пространстве, поэтому каждый из данных векторов соотношения можно разложить по векторам базиса, причем единственным образом:

Предположим, что для некоторого вектора, не входящего в базис, например для вектора А_m+1, является положительным хотя бы один из коэффициентов х_i,_m+1 в разложении

(1.16)

Зададимся некоторой величиной q > 0 (пока неизвестной), умножим на нее обе части равенства (1.16) и вычтем результат почленно из равенства (1.15). Получаем

Таким образом, вектор

является планом, если его компоненты неотрицательны.

Так как q>0, то все компоненты вектора Х₁, в которые входят неположительные x_i,_m+1, неотрицательны. Поэтому надо рассмотреть только компоненты, включающие положительные х_i,_m+1 (i=1, 2,...,m), т. е. необходимо определить такое q>0, при котором для всех х_i, _m+1і0.

Из неравенства х_i-q _xi,m+1і0 получаем qЈx_i/x_i,m+1, следовательно, вектор x_i является планом задачи для любого q, удовлетворяющего условию

(1.17)

где минимум берется по i, для которых x_i,m+1>0.

Опорный план не может содержать (m + 1) положительных компонент, поэтому в плане Х₁ необходимо обратить в нуль по крайней мере одну из компонент. Положим в (1.17), что

тогда компонента плана X₁, для которой достигается минимум, обращается в нуль. Пусть эта компонента стоит на первом месте, т. е.

Подставляя значение q₀ в (7), получаем разложение

которому, соответствует новый опорный план:

где х_i' = x_i - q₀x_i,m+1 (i = 2, 3,..., m), х'_m+1 = q₀.

Исключение одного вектора из базиса и включение вместо него другого с помощью q₀ соответствуют переходу от одного базиса к другому с помощью метода Жордана – Гаусса, поэтому система векторов А₂, А₃,…, А_m, А_m+1 линейно независима и является новым базисом.

Для определения следующего опорного плана необходимо любой вектор, не входящий в базис А₂, А₃,..., А_m, А_m+1, разложить по векторам этого базиса, а затем определить такое q₀ > 0, при котором исключался бы один из векторов этого базиса.

Таким образом, процесс получения новых опорных планов заключается в выборе вектора, который подлежит включению в базис, и определении вектора, подлежащего исключению из базиса. Критерий, используемый для определения вектора, который включается в базис, является одним из основных элементов симплексного метода. Заметим, что если вектор А_m+1 подлежит включению в базис, а в его разложении все x_i,m+1Ј0, то, очевидно, нельзя выбрать такое q > 0, которое исключало бы один из векторов разложения. В этом случае план Х₁ содержит m + 1 положительных компонент, а система векторов А₁, А₂, А₃,..., А_m, А_m+1 является линейно зависимой и определяет не угловую, а внутреннюю точку многогранника решений, в которой линейная функция не может достигать минимального значения. Это указывает на то, что гиперплоскость, соответствующая линейной функции, не может стать опорной к многограннику решений, как бы далеко ни перемещать ее в направлении, обратном вектору N, т. е. линейная функция не ограничена на многограннике решений.

Таким образом, если система ограничений задачи линейного программирования при неотрицательных свободных членах содержит единичный базис, то без дополнительных вычислений можно получить первоначальный опорный план, а также коэффициенты разложения векторов по векторам базиса.

 

1.4. Отыскание оптимального плана. Условия оптимальности

Предположим, что задача линейного программирования (1.11)-(1.13) обладает планами и каждый ее опорный план невырожден. В этом случае для опорного плана (1.15) имеем:

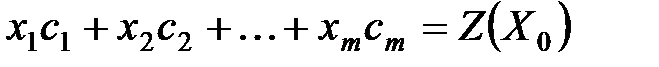
где все X_i > О, а Z (Хо) - значение линейной функции, соответствующее этому плану.

Разложение любого вектора А_j по векторам данного базиса А₁, А₂,..., А_m единственное:

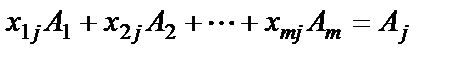
поэтому разложению вектора А_j в базисе соответствует и единственное значение линейной функции

где Z_j – значение линейной функции, если в нее вместо неизвестных подставить соответствующие коэффициенты разложения j-го вектора по векторам базиса.

Обозначим через C_j коэффициент в линейной функции, соответствующий вектору А_j. Тогда справедлива следующая теорема:

Если для некоторого вектора A_j выполняется условие Z_j-C_j>0, то план Х₀ не является оптимальным, и можно построить такой план X, для которого выполняется неравенство Z(Х) < Z(X₀).

Доказательство. Умножая на q>0 и вычитая результаты соответственно, получим:

	(1.18)
	(1.19)

 

В соотношении (1.19) к обеим частям прибавлена величина qC_j для j = 1, 2,..., n. В (11) x₁, х₂,..., х_m положительны, поэтому всегда можно выбрать такое q > 0, чтобы все коэффициенты при векторах А₁, А₂,..., А_m, А_j были неотрицательными, т. е. получить новый план задачи: X = (х₁ - qх_1j, х₂ - qх_2j,..., х_m - qх_mj, q, 0,…, 0) которому согласно соответствует значение линейной функции

(1.20)

Так как по условию теоремы Z_j-C_j>0 и q > 0, то

Z(X)<Z(X₀).

С л е д с т в и е. Если для некоторого плана Х₀ разложения всех векторов А_j (j=1, 2,..., n) в данном базисе удовлетворяют условию

Zj-Cj Ј 0

(1.21)

то план Х₀ является оптимальным.

Неравенства (1.21) являются условием оптимальности плана задачи, решаемой на отыскание минимального значения линейной функции, а значения Z_j-C_j называются оценками плана.

Таким образом, для того чтобы план задачи на отыскание минимального значения линейной функции был оптимальным, необходимо и достаточно, чтобы его оценки были неположительными.

Для задачи линейного программирования (1.11)-(1.13), заключающейся в отыскании максимального значения линейной функции, справедлива следующая теорема:

Если для некоторого вектора А_j выполняется условие Z_j-C_j < 0, то план Х₀ не является оптимальным и можно построить такой план X, для которого выполняется условие Z(X) > Z(X₀).

Доказательство аналогично доказательству предыдущей теоремы.

С л е д с т в и е. Если для некоторого плана Х₀ разложения всех векторов А_j (j=1, 2,...,n) в данном базисе удовлетворяют условию

Zj-Cj і 0

(1.22)

то план Х₀ является оптимальным.

Неравенства (1.22) являются условием оптимальности плана задачи на отыскание максимального значения линейной функции.

Таким образом, для того чтобы план задачи на отыскание максимального значения линейной функции был оптимальным, необходимо и достаточно, чтобы его оценки были неотрицательными [1].