Пусть задан ориентированный (или неориентированный) граф  в котором
в котором  – множество вершин, а
– множество вершин, а 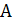 – множество дуг. Припишем каждой дуге
– множество дуг. Припишем каждой дуге  «длину»
«длину»  .
.
Определение 1. Путь  из вершины
из вершины  в вершину
в вершину  определим как последовательность дуг, которая начинается в
определим как последовательность дуг, которая начинается в  и заканчивается в
и заканчивается в  , в которой конец предшествующей дуги является началом следующей. Сумму длин дуг, входящих в путь, назовем длиной пути.
, в которой конец предшествующей дуги является началом следующей. Сумму длин дуг, входящих в путь, назовем длиной пути.
Задачи построения кратчайших путей естественно возникают во множестве приложений. Например, если в сети связи информация из источника должна достичь получателей за минимальное время, то, построив граф, в котором длина дуги совпадает с временем прохождения сигнала по этой дуге, мы сведем проблему к задаче построения дерева кратчайших путей (ДКП) из источника к приемникам сигнала.
Если требуется построить сеть дорог, связывающих заданное множество городов, таким образом, чтобы время поездки из одного города в другой было минимальным, то нужно найти кратчайшие пути между всеми парами городов.
3.1. Алгоритм Дейкстры
Алгоритм изобретен нидерландским ученым Э. Дейкстрой
в 1959 г. [4] и строит ДКП из начальной вершины (корня) графа во все остальные вершины при неотрицательных длинах дуг (ребер).
Пусть  – начальная вершина (источник). Алгоритм на каждом шаге добавляет к частично построенному дереву
– начальная вершина (источник). Алгоритм на каждом шаге добавляет к частично построенному дереву  с корнем в
с корнем в  одну ближайшую к
одну ближайшую к  вершину, не принадлежащую
вершину, не принадлежащую  . Если требуется найти кратчайший путь до некоторой вершины
. Если требуется найти кратчайший путь до некоторой вершины 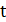 , то алгоритм останавливается после добавления этой вершины. Иначе, строится остовное дерево, связывающее все вершины графа кратчайшими путями с
, то алгоритм останавливается после добавления этой вершины. Иначе, строится остовное дерево, связывающее все вершины графа кратчайшими путями с  , т. е. ДКП.
, т. е. ДКП.
Обозначим через  – множество вершин, из которых есть дуги в вершину
– множество вершин, из которых есть дуги в вершину  в графе
в графе 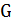 . Положим начальное строящееся дерево
. Положим начальное строящееся дерево  . Припишем каждой вершине
. Припишем каждой вершине  метку
метку  , соответствующую (текущей) минимальной длине пути из
, соответствующую (текущей) минимальной длине пути из  в
в  . Метка источника
. Метка источника  не меняется в процессе работы алгоритма. Сначала
не меняется в процессе работы алгоритма. Сначала  для всех
для всех  . На каждом шаге алгоритма ищется дуга
. На каждом шаге алгоритма ищется дуга  которая добавляется в
которая добавляется в  , и обновляется метка j-ой вершины
, и обновляется метка j-ой вершины  . После этого (с константной трудоемкостью) обновляется метка каждой не включенной в
. После этого (с константной трудоемкостью) обновляется метка каждой не включенной в  вершины
вершины 
Алгоритм останавливается, когда все вершины графа включены в дерево  (после выполнения
(после выполнения  шагов). Трудоемкость одного шага (выбор вершины для включения в
шагов). Трудоемкость одного шага (выбор вершины для включения в  ) равна
) равна  . Следовательно, общая трудоемкость алгоритма Дейкстры –
. Следовательно, общая трудоемкость алгоритма Дейкстры – 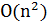 .
.
3.2. Алгоритм Беллмана – Форда
Если длины некоторых ребер (дуг) принимают отрицательные значения, то в случае отсутствия циклов отрицательной длины кратчайшие пути из одной вершины во все остальные строит алгоритм Беллмана – Форда [4].
Введем  – номер вершины, непосредственно предшествующей вершине
– номер вершины, непосредственно предшествующей вершине  в пути
в пути  . Тогда алгоритм Беллмана – Форда можно записать по шагам следующим образом.
. Тогда алгоритм Беллмана – Форда можно записать по шагам следующим образом.
Шаг 1. Для каждой вершины  : если
: если  , то положить
, то положить  ; иначе положить
; иначе положить  и
и  .
.
Шаг 2. Для каждой вершины  и для каждого ребра
и для каждого ребра  : если
: если  , то положить
, то положить  и
и  .
.
Шаг 3. Для каждого ребра  : если
: если  , то граф содержит отрицательный цикл.
, то граф содержит отрицательный цикл.
Корректность приведенного алгоритма можно доказать по индукции.
Лемма 2.1. После выполнения  итераций:
итераций:
1) если  , то
, то  – длина некоторого пути из
– длина некоторого пути из  в
в 
2) если существует путь из  в
в  , содержащий не более
, содержащий не более  ребер, то
ребер, то  не превосходит длины кратчайшего пути из
не превосходит длины кратчайшего пути из  в
в  , содержащего не более
, содержащего не более  ребер.
ребер.
Доказательство. На нулевой итерации  длина пути, не содержащего ребер,
длина пути, не содержащего ребер,  . Для других вершин
. Для других вершин  т. к. не существует путей из источника в
т. к. не существует путей из источника в  с нулевым числом ребер. Докажем первое утверждение. Рассмотрим случай, когда длина пути в вершину
с нулевым числом ребер. Докажем первое утверждение. Рассмотрим случай, когда длина пути в вершину  меняется, т. е. выполняется присваивание
меняется, т. е. выполняется присваивание  . По индуктивному предположению,
. По индуктивному предположению,  – это длина некоторого пути из источника в
– это длина некоторого пути из источника в  . Значит, величина
. Значит, величина  равна длине пути
равна длине пути 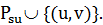
Для доказательства второго утверждения рассмотрим кратчайший путь из  в
в  , содержащий не более
, содержащий не более  ребер. Пусть
ребер. Пусть  – предпоследняя вершина этого пути. Тогда часть пути из
– предпоследняя вершина этого пути. Тогда часть пути из  в
в  является кратчайшим путем из источника в
является кратчайшим путем из источника в  , содержащего не более
, содержащего не более  ребер. По индуктивному предположению,
ребер. По индуктивному предположению,  после
после  итерации не превосходит длины этого пути. Следовательно,
итерации не превосходит длины этого пути. Следовательно,  не превосходит длины пути из
не превосходит длины пути из  в
в  . На i-ой итерации величина
. На i-ой итерации величина  сравнивается с
сравнивается с  и ей присваивается новое значение, если
и ей присваивается новое значение, если  меньше. Следовательно, после i-ой итерации
меньше. Следовательно, после i-ой итерации  не превосходит длины кратчайшего пути из источника в
не превосходит длины кратчайшего пути из источника в  , содержащего не более
, содержащего не более  ребер. ∎
ребер. ∎
Если в графе нет отрицательных циклов, то в каждую вершину строится единственный путь минимальной длины, и на шаге 3 не может произойти уменьшение длины ни одного пути. В противном случае отрицательный цикл существует.
3.3. Алгоритм Флойда – Уоршелла
Алгоритм Флойда – Уоршелла (Floyd–Warshall) разработан в 1962 г. [4] и используется для нахождения кратчайших расстояний между всеми парами вершин взвешенного ориентированного графа.
Введем обозначение  для длины кратчайшего пути из
для длины кратчайшего пути из  в
в  , который, кроме самих вершин
, который, кроме самих вершин  проходит только через вершины множества
проходит только через вершины множества  Тогда
Тогда  – длина дуги
– длина дуги  , если она существует; иначе
, если она существует; иначе 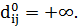
Если кратчайший путь из  в
в  не проходит через вершину
не проходит через вершину  , тогда
, тогда  . Если существует более короткий путь из
. Если существует более короткий путь из  в
в  , проходящий через
, проходящий через  , тогда
, тогда  . Рекуррентная формула для вычисления
. Рекуррентная формула для вычисления  имеет вид:
имеет вид: 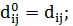

Алгоритм Флойда – Уоршелла последовательно вычисляет все значения  для всех
для всех  Значения
Значения  являются длинами кратчайших путей между вершинами
являются длинами кратчайших путей между вершинами  и
и  . Несложно понять, что трудоемкость алгоритма –
. Несложно понять, что трудоемкость алгоритма –  . Если дополнительно для каждой пары вершин хранить информацию о первой вершине пути, то, помимо расстояния между двумя узлами, получим возможность восстановить сами кратчайшие пути.
. Если дополнительно для каждой пары вершин хранить информацию о первой вершине пути, то, помимо расстояния между двумя узлами, получим возможность восстановить сами кратчайшие пути.
Не существует кратчайшего пути между парой вершин  который является частью отрицательного цикла, т. к. длина пути из
который является частью отрицательного цикла, т. к. длина пути из  в
в  может быть сколь угодно мала (отрицательна). По умолчанию, применение алгоритма подразумевает отсутствие отрицательных циклов в графе. Однако если отрицательный цикл есть, алгоритм Флойда – Уоршелла можно использовать для его поиска:
может быть сколь угодно мала (отрицательна). По умолчанию, применение алгоритма подразумевает отсутствие отрицательных циклов в графе. Однако если отрицательный цикл есть, алгоритм Флойда – Уоршелла можно использовать для его поиска:
– алгоритм итеративно пересчитывает длины кратчайших путей между каждой парой вершин  в том числе и
в том числе и 
– сначала все длины пути из  в
в  равны нулю;
равны нулю;
– длина пути  может быть меньше в случае, если она отрицательная, т. е. это отрицательный цикл;
может быть меньше в случае, если она отрицательная, т. е. это отрицательный цикл;
– значит, после остановки алгоритма длина пути из  в
в  будет отрицательной, если существует цикл отрицательной длины из
будет отрицательной, если существует цикл отрицательной длины из  в
в  .
.
Следовательно, для определения отрицательного цикла с помощью алгоритма Флойда – Уоршелла достаточно просмотреть диагональ матрицы  . Присутствие на диагонали отрицательных чисел говорит о наличии в графе как минимум одного отрицательного цикла. Очевидно, в неориентированном графе ребро отрицательной длины вместе с инцидентными ему вершинами образует отрицательный цикл.
. Присутствие на диагонали отрицательных чисел говорит о наличии в графе как минимум одного отрицательного цикла. Очевидно, в неориентированном графе ребро отрицательной длины вместе с инцидентными ему вершинами образует отрицательный цикл.
3.4. Примеры и упражнения
Пример 3.1. Построить дерево кратчайших расстояний из вершины s во все вершины ориентированного графа, изображенного на рис. 3.1a (рядом с дугами указаны их длины), с помощью алгоритма Дейкстры.

Рисунок-3.1. Иллюстрация работы алгоритма Дейкстры
Решение. Положим длины кратчайших путей в вершины (метки вершин) равными  , и частично построенное дерево кратчайших путей
, и частично построенное дерево кратчайших путей  . Найдем
. Найдем  и положим
и положим  Метки других вершин не изменятся, т. к. из вершины 4 не исходит ни одна дуга.
Метки других вершин не изменятся, т. к. из вершины 4 не исходит ни одна дуга.
Найдем  и положим
и положим  . Обновим метку вершины 1:
. Обновим метку вершины 1: 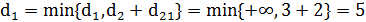 . Метки других вершин не изменятся. Продолжая процесс, добавим последовательно в строящееся дерево ребра
. Метки других вершин не изменятся. Продолжая процесс, добавим последовательно в строящееся дерево ребра  и вершины 5, 1, 3, 6. В результате будет построено дерево, показанное на рис. 2.1b, в котором метки рядом с вершинами – длины кратчайших путей из источника
и вершины 5, 1, 3, 6. В результате будет построено дерево, показанное на рис. 2.1b, в котором метки рядом с вершинами – длины кратчайших путей из источника  .
.
Пример 3.2. Найти длины кратчайших путей между всеми парами вершин графа, изображенного на рис. 3.1a, с помощью алгоритма Флойда – Уоршелла.
Решение. Зададим начальные длины путей между вершинами матрицей с элементами  полагая
полагая  (рис. 3.2a, на котором символ «-» соответствует бесконечности). Воспользуемся рекуррентными соотношениями
(рис. 3.2a, на котором символ «-» соответствует бесконечности). Воспользуемся рекуррентными соотношениями  для вычисления длин путей после первой итерации (рис. 2.2b).
для вычисления длин путей после первой итерации (рис. 2.2b).
|
| -
|
| -
| -
|
|
| |
|
| -
|
| -
| -
| -
| | -
| -
|
| -
| -
|
| -
| | -
| -
| -
|
| -
| -
| -
| | -
| -
| -
| -
|
| -
| -
| | -
| -
| -
| -
| -
|
|
| | -
|
| -
|
|
| -
|
|
| |
|
|
|
|
|
|
| |
|
|
|
| -
|
|
| | -
| -
|
| -
| -
|
|
| | -
| -
| -
|
| -
| -
| -
| | -
| -
| -
| -
|
| -
| -
| | -
|
| -
|
|
|
|
| |
|
| -
|
|
| -
|
|
|
a) 
| b) 
|
Рисунок-3.2. Матрица начальных расстояний (a) и после первой итерации (b)
Рисунок-3.3. Матрица кратчайших расстояний между всеми парами вершин
Очевидно, что из вершин 4 и 5 нет путей в другие вершины, поэтому бесконечности в этих строках сохранятся как после первой итерации, так и в дальнейшем.
После 4 итерации получим окончательные значения для минимальных длин путей, связывающих все пары вершин (рис. 3.3).
Упражнение 3.1. Доказать, что алгоритм Дейкстры строит дерево кратчайших расстояний.
Упражнение 3.2. Найти кратчайшие пути между всеми парами вершин графа, изображенного на рис. 2.1a.
Упражнение 3.3. Существует ли отрицательный цикл в графе, изображенном на рис. 2.4?
Упражнение 3.4. Воспользуйтесь алгоритмом Беллмана – Форда для построения кратчайших путей из вершины  в графе, изображенном на рис. 2.4, удалив входящие в
в графе, изображенном на рис. 2.4, удалив входящие в  дуги.
дуги.
Упражнение 3.5. Доказать корректность алгоритма Флойда – Уоршелла.

Рисунок-3.4. Ориентированный взвешенный граф
(рядом с дугами указаны их длины)
Упражнение 3.6. Профессор О. П. Рометчивый предлагает следующий способ нахождения кратчайшего пути из  в
в 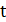 в данном ориентированном графе, содержащем рёбра отрицательного веса. Прибавим достаточно большую константу к весам всех рёбер и сделаем все веса положительными, после чего воспользуемся алгоритмом Дейкстры. Корректен ли такой подход? Если да, то докажите это, если нет –– укажите контрпример.
в данном ориентированном графе, содержащем рёбра отрицательного веса. Прибавим достаточно большую константу к весам всех рёбер и сделаем все веса положительными, после чего воспользуемся алгоритмом Дейкстры. Корректен ли такой подход? Если да, то докажите это, если нет –– укажите контрпример.
Упражнение 3.7. Рассмотрим ориентированный граф, в котором рёбра отрицательного веса выходят только из вершины s, но циклов отрицательного веса при этом нет. Может ли алгоритм Дейкстры, вызванный для вершины  , выдать неправильный ответ в данном случае?
, выдать неправильный ответ в данном случае?
Упражнение 3.8. Пусть неориентированный граф  задаёт множество городов и дорог между ними. Для каждой дороги
задаёт множество городов и дорог между ними. Для каждой дороги  известна её длина в километрах
известна её длина в километрах  . Предположим, что вам необходимо добраться из города
. Предположим, что вам необходимо добраться из города  в город
в город 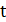 , но ваша машина может проехать без дозаправки не больше
, но ваша машина может проехать без дозаправки не больше  километров. Заправки есть во всех городах, но не вдоль дорог (так что годятся только маршруты, где все рёбра не длиннее
километров. Заправки есть во всех городах, но не вдоль дорог (так что годятся только маршруты, где все рёбра не длиннее  ).
).
(a) Постройте алгоритм, определяющий за линейное время, можно ли при таких ограничениях добраться из  в
в 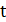 .
.
(b) Допустим теперь, что вы хотите купить новую машину. Какой минимальный объём бака машины позволит добраться из  в
в 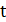 ? Постройте алгоритм, дающий ответ за время
? Постройте алгоритм, дающий ответ за время  .
.
Упражнение 3.9. Пусть граф  представляет собой множество городов
представляет собой множество городов 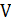 и множество дорог
и множество дорог 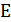 между ними. У каждой дороги
между ними. У каждой дороги  есть длина
есть длина  . Решено построить новую дорогу, и список
. Решено построить новую дорогу, и список  содержит пары вершин, между которыми новая дорога может быть построена. Для всех возможных новых дорог
содержит пары вершин, между которыми новая дорога может быть построена. Для всех возможных новых дорог  известна длина
известна длина  . Надо найти дорогу из
. Надо найти дорогу из  , строительство которой приведёт к максимальному уменьшению длины кратчайшего пути между заданными двумя городами
, строительство которой приведёт к максимальному уменьшению длины кратчайшего пути между заданными двумя городами  и
и 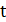 в
в 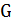 . Постройте эффективный алгоритм для такой задачи.
. Постройте эффективный алгоритм для такой задачи.
Упражнение 3.10. Применения задачи о кратчайших путях можно найти даже в валютных операциях. Пусть через 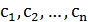 обозначены различные валюты. Например,
обозначены различные валюты. Например,  может обозначать рубли,
может обозначать рубли,  –– доллары,
–– доллары,  –– фунты. Пусть через
–– фунты. Пусть через 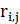 обозначен курс конвертации валюты
обозначен курс конвертации валюты  в
в 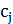 : на одну единицу валюты
: на одну единицу валюты  можно купить
можно купить 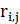 единиц валюты
единиц валюты 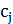 . Данные курсы удовлетворяют естественному условию
. Данные курсы удовлетворяют естественному условию  , которое говорит, что обмен туда-обратно невыгоден.
, которое говорит, что обмен туда-обратно невыгоден.
(a) Постройте эффективный алгоритм, который, зная все 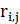 , находит наиболее выгодную последовательность обменов для конвертации заданной валюты
, находит наиболее выгодную последовательность обменов для конвертации заданной валюты  в заданную валюту
в заданную валюту 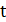 . (Подсказка: для решения задачи представьте входные данные в виде графа с вещественными весами.)
. (Подсказка: для решения задачи представьте входные данные в виде графа с вещественными весами.)
Под влиянием спроса и предложения курсы валют меняются. Представим, что в какой-то момент нашлись валюты  , для которых
, для которых  . Это означает, что обменяв какое-то количество валюты
. Это означает, что обменяв какое-то количество валюты  в соответствии с данной последовательностью, мы в итоге получим больше исходного. (Вряд ли это продлится долго, но обидно упустить такую возможность!)
в соответствии с данной последовательностью, мы в итоге получим больше исходного. (Вряд ли это продлится долго, но обидно упустить такую возможность!)
(b) Постройте эффективный алгоритм, проверяющий наличие такой аномальной ситуации. (Подсказка: используйте граф предыдущего пункта.)
Упражнение 3.11. Задача о путешествующем пароходе. Представьте, что у вас есть пароход, который может совершать рейсы между портовыми городами из множества 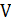 . Посещая город
. Посещая город  , вы зарабатываете
, вы зарабатываете  рублей, а стоимость перемещения из города
рублей, а стоимость перемещения из города  в город
в город  составляет
составляет 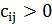 рублей. Вы хотите найти циклический маршрут, максимизирующий отношение прибыли к затратам.
рублей. Вы хотите найти циклический маршрут, максимизирующий отношение прибыли к затратам.
Для этого рассмотрим ориентированный граф  , где вершинами являются города и каждые две вершины соединены ребром. Определим относительную прибыль цикла C следующим образом:
, где вершинами являются города и каждые две вершины соединены ребром. Определим относительную прибыль цикла C следующим образом: 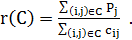
Через 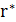 обозначим максимальную относительную прибыль простого цикла. Значение
обозначим максимальную относительную прибыль простого цикла. Значение 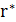 можно найти двоичным поиском, если мы умеем проверять по данному
можно найти двоичным поиском, если мы умеем проверять по данному 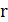 , верно ли неравенство
, верно ли неравенство  .
.
Итак, рассмотрим произвольное 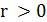 . Присвоим каждому ребру
. Присвоим каждому ребру  вес
вес  .
.
(a) Покажите, что если в этом графе есть цикл отрицательного веса, то  .
.
(b) Покажите, что если все циклы имеют строго положительный вес, то  .
.
(c) Постройте эффективный алгоритм, который для заданной точности  находит цикл
находит цикл 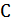 , для которого
, для которого  . Докажите корректность алгоритма и оцените его время работы в терминах
. Докажите корректность алгоритма и оцените его время работы в терминах  , и
, и  .
.
ЗАДАЧА ШТЕЙНЕРА
Пусть на плоскости расположены три точки, расстояния между которыми определяются евклидовой метрикой, и требуется связать эти точки с помощью МОД. Построенное дерево показано на рис. 4.1a, и его длина (сумма длин ребер) равна 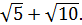

| Рисунок-4.1.Минимальное остовное дерево(a)и дерево Штейнера(b)
|
Введем дополнительную (промежуточную) точку и соединим исходные точки с промежуточной точкой. В результате получим связывающее дерево меньшей длины 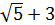 (по сравнению с МОД) (рис. 4.1b). Это дерево является геометрическим (или метрическим) деревом Штейнера, и в него вошла одна дополнительная точка (2, 2) – вершина Штейнера. При построении метрического дерева Штейнера для уменьшения длины дерева можно использовать любые дополнительные точки на плоскости.
(по сравнению с МОД) (рис. 4.1b). Это дерево является геометрическим (или метрическим) деревом Штейнера, и в него вошла одна дополнительная точка (2, 2) – вершина Штейнера. При построении метрического дерева Штейнера для уменьшения длины дерева можно использовать любые дополнительные точки на плоскости.
Далее будем рассматривать задачу Штейнера на графах, формулировка которой приводится в следующем разделе. В последней задаче точки Штейнера выбираются из заданного множества вершин графа.



 в котором
в котором  – множество вершин, а
– множество вершин, а 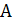 – множество дуг. Припишем каждой дуге
– множество дуг. Припишем каждой дуге  «длину»
«длину»  .
. из вершины
из вершины  в вершину
в вершину  определим как последовательность дуг, которая начинается в
определим как последовательность дуг, которая начинается в  – начальная вершина (источник). Алгоритм на каждом шаге добавляет к частично построенному дереву
– начальная вершина (источник). Алгоритм на каждом шаге добавляет к частично построенному дереву  с корнем в
с корнем в 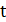 , то алгоритм останавливается после добавления этой вершины. Иначе, строится остовное дерево, связывающее все вершины графа кратчайшими путями с
, то алгоритм останавливается после добавления этой вершины. Иначе, строится остовное дерево, связывающее все вершины графа кратчайшими путями с  – множество вершин, из которых есть дуги в вершину
– множество вершин, из которых есть дуги в вершину 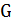 . Положим начальное строящееся дерево
. Положим начальное строящееся дерево  . Припишем каждой вершине
. Припишем каждой вершине  метку
метку  , соответствующую (текущей) минимальной длине пути из
, соответствующую (текущей) минимальной длине пути из  не меняется в процессе работы алгоритма. Сначала
не меняется в процессе работы алгоритма. Сначала  для всех
для всех  . На каждом шаге алгоритма ищется дуга
. На каждом шаге алгоритма ищется дуга  которая добавляется в
которая добавляется в  . После этого (с константной трудоемкостью) обновляется метка каждой не включенной в
. После этого (с константной трудоемкостью) обновляется метка каждой не включенной в 
 шагов). Трудоемкость одного шага (выбор вершины для включения в
шагов). Трудоемкость одного шага (выбор вершины для включения в  . Следовательно, общая трудоемкость алгоритма Дейкстры –
. Следовательно, общая трудоемкость алгоритма Дейкстры – 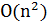 .
. – номер вершины, непосредственно предшествующей вершине
– номер вершины, непосредственно предшествующей вершине  в пути
в пути  . Тогда алгоритм Беллмана – Форда можно записать по шагам следующим образом.
. Тогда алгоритм Беллмана – Форда можно записать по шагам следующим образом. : если
: если  , то положить
, то положить  ; иначе положить
; иначе положить  и
и  .
. и для каждого ребра
и для каждого ребра  : если
: если  , то положить
, то положить  и
и  .
. , то
, то  – длина некоторого пути из
– длина некоторого пути из 
 , содержащий не более
, содержащий не более  длина пути, не содержащего ребер,
длина пути, не содержащего ребер,  т. к. не существует путей из источника в
т. к. не существует путей из источника в  равна длине пути
равна длине пути 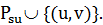
 ребер. По индуктивному предположению,
ребер. По индуктивному предположению,  после
после  итерации не превосходит длины этого пути. Следовательно,
итерации не превосходит длины этого пути. Следовательно,  не превосходит длины пути из
не превосходит длины пути из  и ей присваивается новое значение, если
и ей присваивается новое значение, если  для длины кратчайшего пути из
для длины кратчайшего пути из  проходит только через вершины множества
проходит только через вершины множества  Тогда
Тогда  – длина дуги
– длина дуги  , если она существует; иначе
, если она существует; иначе 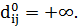
 , тогда
, тогда  . Если существует более короткий путь из
. Если существует более короткий путь из  . Рекуррентная формула для вычисления
. Рекуррентная формула для вычисления 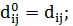

 Значения
Значения  являются длинами кратчайших путей между вершинами
являются длинами кратчайших путей между вершинами  . Если дополнительно для каждой пары вершин хранить информацию о первой вершине пути, то, помимо расстояния между двумя узлами, получим возможность восстановить сами кратчайшие пути.
. Если дополнительно для каждой пары вершин хранить информацию о первой вершине пути, то, помимо расстояния между двумя узлами, получим возможность восстановить сами кратчайшие пути.
 может быть меньше в случае, если она отрицательная, т. е. это отрицательный цикл;
может быть меньше в случае, если она отрицательная, т. е. это отрицательный цикл; . Присутствие на диагонали отрицательных чисел говорит о наличии в графе как минимум одного отрицательного цикла. Очевидно, в неориентированном графе ребро отрицательной длины вместе с инцидентными ему вершинами образует отрицательный цикл.
. Присутствие на диагонали отрицательных чисел говорит о наличии в графе как минимум одного отрицательного цикла. Очевидно, в неориентированном графе ребро отрицательной длины вместе с инцидентными ему вершинами образует отрицательный цикл. , и частично построенное дерево кратчайших путей
, и частично построенное дерево кратчайших путей  и положим
и положим  Метки других вершин не изменятся, т. к. из вершины 4 не исходит ни одна дуга.
Метки других вершин не изменятся, т. к. из вершины 4 не исходит ни одна дуга. и положим
и положим  . Обновим метку вершины 1:
. Обновим метку вершины 1: 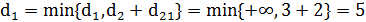 . Метки других вершин не изменятся. Продолжая процесс, добавим последовательно в строящееся дерево ребра
. Метки других вершин не изменятся. Продолжая процесс, добавим последовательно в строящееся дерево ребра  и вершины 5, 1, 3, 6. В результате будет построено дерево, показанное на рис. 2.1b, в котором метки рядом с вершинами – длины кратчайших путей из источника
и вершины 5, 1, 3, 6. В результате будет построено дерево, показанное на рис. 2.1b, в котором метки рядом с вершинами – длины кратчайших путей из источника  полагая
полагая  (рис. 3.2a, на котором символ «-» соответствует бесконечности). Воспользуемся рекуррентными соотношениями
(рис. 3.2a, на котором символ «-» соответствует бесконечности). Воспользуемся рекуррентными соотношениями  для вычисления длин путей после первой итерации (рис. 2.2b).
для вычисления длин путей после первой итерации (рис. 2.2b).

 в графе, изображенном на рис. 2.4, удалив входящие в
в графе, изображенном на рис. 2.4, удалив входящие в  дуги.
дуги. задаёт множество городов и дорог между ними. Для каждой дороги
задаёт множество городов и дорог между ними. Для каждой дороги  известна её длина в километрах
известна её длина в километрах  . Предположим, что вам необходимо добраться из города
. Предположим, что вам необходимо добраться из города  километров. Заправки есть во всех городах, но не вдоль дорог (так что годятся только маршруты, где все рёбра не длиннее
километров. Заправки есть во всех городах, но не вдоль дорог (так что годятся только маршруты, где все рёбра не длиннее  .
. представляет собой множество городов
представляет собой множество городов 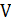 и множество дорог
и множество дорог 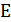 между ними. У каждой дороги
между ними. У каждой дороги  содержит пары вершин, между которыми новая дорога может быть построена. Для всех возможных новых дорог
содержит пары вершин, между которыми новая дорога может быть построена. Для всех возможных новых дорог  известна длина
известна длина  . Надо найти дорогу из
. Надо найти дорогу из 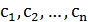 обозначены различные валюты. Например,
обозначены различные валюты. Например,  может обозначать рубли,
может обозначать рубли,  –– доллары,
–– доллары,  –– фунты. Пусть через
–– фунты. Пусть через 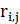 обозначен курс конвертации валюты
обозначен курс конвертации валюты  в
в 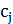 : на одну единицу валюты
: на одну единицу валюты  , которое говорит, что обмен туда-обратно невыгоден.
, которое говорит, что обмен туда-обратно невыгоден. , для которых
, для которых  . Это означает, что обменяв какое-то количество валюты
. Это означает, что обменяв какое-то количество валюты  в соответствии с данной последовательностью, мы в итоге получим больше исходного. (Вряд ли это продлится долго, но обидно упустить такую возможность!)
в соответствии с данной последовательностью, мы в итоге получим больше исходного. (Вряд ли это продлится долго, но обидно упустить такую возможность!) рублей, а стоимость перемещения из города
рублей, а стоимость перемещения из города 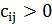 рублей. Вы хотите найти циклический маршрут, максимизирующий отношение прибыли к затратам.
рублей. Вы хотите найти циклический маршрут, максимизирующий отношение прибыли к затратам.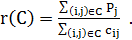
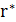 обозначим максимальную относительную прибыль простого цикла. Значение
обозначим максимальную относительную прибыль простого цикла. Значение 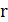 , верно ли неравенство
, верно ли неравенство  .
.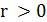 . Присвоим каждому ребру
. Присвоим каждому ребру  вес
вес  .
. .
. находит цикл
находит цикл 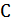 , для которого
, для которого  . Докажите корректность алгоритма и оцените его время работы в терминах
. Докажите корректность алгоритма и оцените его время работы в терминах  , и
, и  .
.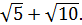
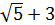 (по сравнению с МОД) (рис. 4.1b). Это дерево является геометрическим (или метрическим) деревом Штейнера, и в него вошла одна дополнительная точка (2, 2) – вершина Штейнера. При построении метрического дерева Штейнера для уменьшения длины дерева можно использовать любые дополнительные точки на плоскости.
(по сравнению с МОД) (рис. 4.1b). Это дерево является геометрическим (или метрическим) деревом Штейнера, и в него вошла одна дополнительная точка (2, 2) – вершина Штейнера. При построении метрического дерева Штейнера для уменьшения длины дерева можно использовать любые дополнительные точки на плоскости.

