В практических задачах часто требуется построить остовное дерево, удовлетворяющее различным свойствам. В этом разделе приведены некоторые подобные задачи.
МОД ограниченной степени – это минимальное остовное дерево, в котором каждая вершина связана с не более чем  другими вершинами, где
другими вершинами, где  – заданное целое число. Если
– заданное целое число. Если  , то это задача построения минимальной гамильтоновой цепи, откуда следует, что задача построения МОД ограниченной степени NP-трудна в общем случае. Если вершины графа – это точки на плоскости, а веса ребер равны евклидову расстоянию между ними, и требуется построить МОД степени
, то это задача построения минимальной гамильтоновой цепи, откуда следует, что задача построения МОД ограниченной степени NP-трудна в общем случае. Если вершины графа – это точки на плоскости, а веса ребер равны евклидову расстоянию между ними, и требуется построить МОД степени  , то при
, то при  задача полиномиально разрешима [6].
задача полиномиально разрешима [6].
В некоторых приложениях требуется построить такое остовное дерево, в котором максимальный вес ребра минимален. Очевидно, в этом случае МОД является одним из искомых деревьев.
При описании алгоритмов Прима и Краскала мы не налагали ограничений на знак весов ребер, поэтому задача построения остовного дерева максимального веса может быть решена алгоритмами Прима или Краскала после умножения весов ребер на –1 и построения МОД в графе с новыми весами.
Рассмотрим подробнее (в качестве примера) задачу построения сети связи с одним источником минимальной стоимости с ограничением на число узлов коммутации в цепях, связывающих пункты с источником. Эта задача в математической постановке является задачей построения МОД ограниченного радиуса на взвешенном графе с выделенной вершиной, которая может быть поставлена следующим образом.
Задан полный неориентированный взвешенный граф  ,
, 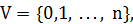 с неотрицательными весами ребер
с неотрицательными весами ребер  . Обозначим
. Обозначим  – множество остовных деревьев графа
– множество остовных деревьев графа 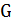 , а
, а  – цепь, связывающая вершину
– цепь, связывающая вершину  с корнем дерева 0 – источником сигнала в дереве
с корнем дерева 0 – источником сигнала в дереве 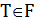 . Требуется построить дерево
. Требуется построить дерево  являющееся решением задачи:
являющееся решением задачи:

| (2.1)
|

| (2.2)
|
где R £ n – заданное положительное целое число, а через 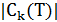 обозначено количество ребер в цепи
обозначено количество ребер в цепи  . Число
. Число  является радиусом дерева
является радиусом дерева  .
.
Задача (2.1) – (2.2) при  является NP-трудной, что естественно вытекает из NP-трудности задачи построения МОД ограниченного диаметра [7]. В работе [8] показана NP-трудность рассматриваемой задачи на максимум, которая тесно связана с задачей (2.1)–(2.2). Действительно, если
является NP-трудной, что естественно вытекает из NP-трудности задачи построения МОД ограниченного диаметра [7]. В работе [8] показана NP-трудность рассматриваемой задачи на максимум, которая тесно связана с задачей (2.1)–(2.2). Действительно, если  , то задача
, то задача  с ограничением (2.2), где
с ограничением (2.2), где  , эквивалентна задаче (2.1) – (2.2).
, эквивалентна задаче (2.1) – (2.2).
В работе [8] для задачи на максимум предложена серия полиномиальных алгоритмов построения решения с гарантированной оценкой относительной погрешности, в наихудшем случае равной 1/2. Если же для весов ребер выполняется неравенство треугольника, то оценка относительной погрешности улучшается до величины  .
.
Для задачи (2.1) – (2.2) полученные априорные оценки точности зависят от параметров задачи и не являются гарантированными [8].
Приведем еще один пример практической задачи выбора дальности передачи элементов радиосети, в которой строится остовное дерево. Эта задача известна в литературе как Min-Power Symmetric Connectivity Problem и заключается в следующем.
Задан простой неориентированный взвешенный граф  с множеством вершин
с множеством вершин  , и множеством ребер
, и множеством ребер 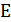 . Пусть
. Пусть  – вес ребра
– вес ребра 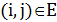 . Требуется найти остовное дерево
. Требуется найти остовное дерево  графа
графа 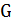 , являющееся решением задачи:
, являющееся решением задачи:

| (2.3)
|
где  – множество вершин, смежных с вершиной
– множество вершин, смежных с вершиной  в дереве T. Любое допустимое решение задачи (2.3) – остовное дерево – назовем также коммуникационным деревом.
в дереве T. Любое допустимое решение задачи (2.3) – остовное дерево – назовем также коммуникационным деревом.
Задача (2.3) NP-трудна в сильном смысле уже в случае, когда вершины – это точки в  , а вес ребра равен евклидову расстоянию между соответствующими точками. В общем случае NP-трудность естественно следует из сводимости задачи о минимальном покрытии (МП) к задаче (2.3).
, а вес ребра равен евклидову расстоянию между соответствующими точками. В общем случае NP-трудность естественно следует из сводимости задачи о минимальном покрытии (МП) к задаче (2.3).
Для любого остовного дерева  справедливы очевидные неравенства
справедливы очевидные неравенства 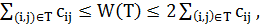 откуда следует, что МОД является
откуда следует, что МОД является  -приближенным решением задачи (2.3). Т.е.
-приближенным решением задачи (2.3). Т.е. 
где  – значение функционала на МОД, а
– значение функционала на МОД, а 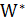 – оптимальное значение целевой функции. Справедлива
– оптимальное значение целевой функции. Справедлива
Теорема 2.1. Пусть веса ребер, вошедших в МОД, принадлежат отрезку  Тогда
Тогда  и при
и при 
Теорема 2.2. Если задача построения k-приближенного решения задачи МП в графе, степени вершин которого не превосходят  ,
,
NP-трудна, то задача построения  -приближенного решения задачи (1.3) также NP-трудна.
-приближенного решения задачи (1.3) также NP-трудна.
Следствие 2.1. Известно, что задача построения  -приближенного решения для проблемы МП при
-приближенного решения для проблемы МП при  NP-трудна. Тогда из теоремы 1.2, в частности, следует NP-трудность построения
NP-трудна. Тогда из теоремы 1.2, в частности, следует NP-трудность построения  -приближенного решения задачи (1.3).
-приближенного решения задачи (1.3).
Примеры и упражнения
Пример 2.1. Построить МОД в графе, изображенном на рис. 2.1a (рядом с ребрами указаны их веса), с помощью алгоритма Прима.
Решение. Положим 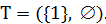 Тогда метки вершин
Тогда метки вершин 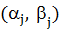 ,
, 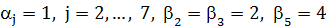 , остальные
, остальные 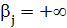 . Вершины 2 и 3, ближайшие к T, добавим, например, вершину 2, получив
. Вершины 2 и 3, ближайшие к T, добавим, например, вершину 2, получив 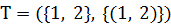 , и пересчитаем метки для вершин 3, …, 7. Получим
, и пересчитаем метки для вершин 3, …, 7. Получим 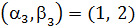 ,
, 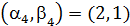 ,
, 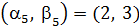 ,
, 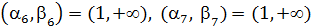 Теперь ближайшая к T вершина 4, добавим ее:
Теперь ближайшая к T вершина 4, добавим ее: 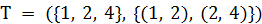 . Продолжая процесс, добавим последовательно вершины 5, 3, 7 и 6 вместе с ребрами (4,5), (1, 3), (5, 7) и (3, 6). МОД изображено на рис. 1.1b, и его вес равен 14.
. Продолжая процесс, добавим последовательно вершины 5, 3, 7 и 6 вместе с ребрами (4,5), (1, 3), (5, 7) и (3, 6). МОД изображено на рис. 1.1b, и его вес равен 14.

Рисунок-2.1.a) граф; b) МОД
Пример 2.2. Найти количество остовных деревьев графа, изображенного на рис. 2.1a, степени которых не превосходят 2.
Решение. Перенумеруем ребра. Очевидно, ребро 1 = (5, 7) войдет во все остовные деревья. Можно построить двоичное дерево решений, начиная с ребра 1, включая (если это не приводит к циклу или превышению допустимой степени вершин) или не включая очередное ребро. В результате получим три гамильтоновых пути. Один из них изображен на рис. 2.1b, два других – на рис. 2.2.

Рисунок-2.2. Два остовных дерева степени 2
Упражнение 2.1. Доказать, что алгоритмы Прима, Краскала и Борувки строят МОД.
Упражнение 2.2. Показать, что в дереве, имеющем две и более вершины, существует как минимум две вершины степени 1.
Упражнение 2.3. Найти такое остовное дерево графа, показанного на рис. 2.1a, в котором максимальный вес ребра минимален.
Упражнение 2.4. Найти МОД графа, показанного на рис. 2.1a, используя алгоритмы Краскала и Борувки.
Упражнение 2.5. Найти все МОД графа, показанного на рис. 2.3.

Рисунок-2.3. Взвешенный граф
(рядом с каждым ребром указан его вес)



 другими вершинами, где
другими вершинами, где  – заданное целое число. Если
– заданное целое число. Если  , то это задача построения минимальной гамильтоновой цепи, откуда следует, что задача построения МОД ограниченной степени NP-трудна в общем случае. Если вершины графа – это точки на плоскости, а веса ребер равны евклидову расстоянию между ними, и требуется построить МОД степени
, то это задача построения минимальной гамильтоновой цепи, откуда следует, что задача построения МОД ограниченной степени NP-трудна в общем случае. Если вершины графа – это точки на плоскости, а веса ребер равны евклидову расстоянию между ними, и требуется построить МОД степени  , то при
, то при  задача полиномиально разрешима [6].
задача полиномиально разрешима [6]. ,
, 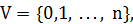 с неотрицательными весами ребер
с неотрицательными весами ребер  . Обозначим
. Обозначим  – множество остовных деревьев графа
– множество остовных деревьев графа 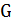 , а
, а  – цепь, связывающая вершину
– цепь, связывающая вершину 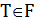 . Требуется построить дерево
. Требуется построить дерево  являющееся решением задачи:
являющееся решением задачи:

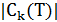 обозначено количество ребер в цепи
обозначено количество ребер в цепи  является радиусом дерева
является радиусом дерева  .
. является NP-трудной, что естественно вытекает из NP-трудности задачи построения МОД ограниченного диаметра [7]. В работе [8] показана NP-трудность рассматриваемой задачи на максимум, которая тесно связана с задачей (2.1)–(2.2). Действительно, если
является NP-трудной, что естественно вытекает из NP-трудности задачи построения МОД ограниченного диаметра [7]. В работе [8] показана NP-трудность рассматриваемой задачи на максимум, которая тесно связана с задачей (2.1)–(2.2). Действительно, если  , то задача
, то задача  с ограничением (2.2), где
с ограничением (2.2), где  , эквивалентна задаче (2.1) – (2.2).
, эквивалентна задаче (2.1) – (2.2). .
. с множеством вершин
с множеством вершин  , и множеством ребер
, и множеством ребер 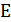 . Пусть
. Пусть  – вес ребра
– вес ребра 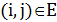 . Требуется найти остовное дерево
. Требуется найти остовное дерево  графа
графа 
 – множество вершин, смежных с вершиной
– множество вершин, смежных с вершиной  в дереве T. Любое допустимое решение задачи (2.3) – остовное дерево – назовем также коммуникационным деревом.
в дереве T. Любое допустимое решение задачи (2.3) – остовное дерево – назовем также коммуникационным деревом. , а вес ребра равен евклидову расстоянию между соответствующими точками. В общем случае NP-трудность естественно следует из сводимости задачи о минимальном покрытии (МП) к задаче (2.3).
, а вес ребра равен евклидову расстоянию между соответствующими точками. В общем случае NP-трудность естественно следует из сводимости задачи о минимальном покрытии (МП) к задаче (2.3).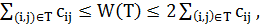 откуда следует, что МОД является
откуда следует, что МОД является  -приближенным решением задачи (2.3). Т.е.
-приближенным решением задачи (2.3). Т.е. 
 – значение функционала на МОД, а
– значение функционала на МОД, а 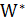 – оптимальное значение целевой функции. Справедлива
– оптимальное значение целевой функции. Справедлива Тогда
Тогда  и при
и при 
 -приближенного решения задачи (1.3) также NP-трудна.
-приближенного решения задачи (1.3) также NP-трудна. -приближенного решения для проблемы МП при
-приближенного решения для проблемы МП при  NP-трудна. Тогда из теоремы 1.2, в частности, следует NP-трудность построения
NP-трудна. Тогда из теоремы 1.2, в частности, следует NP-трудность построения  -приближенного решения задачи (1.3).
-приближенного решения задачи (1.3).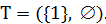 Тогда метки вершин
Тогда метки вершин 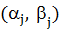 ,
, 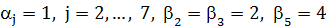 , остальные
, остальные 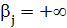 . Вершины 2 и 3, ближайшие к T, добавим, например, вершину 2, получив
. Вершины 2 и 3, ближайшие к T, добавим, например, вершину 2, получив 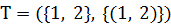 , и пересчитаем метки для вершин 3, …, 7. Получим
, и пересчитаем метки для вершин 3, …, 7. Получим 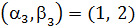 ,
, 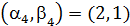 ,
, 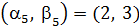 ,
, 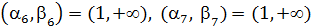 Теперь ближайшая к T вершина 4, добавим ее:
Теперь ближайшая к T вершина 4, добавим ее: 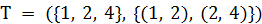 . Продолжая процесс, добавим последовательно вершины 5, 3, 7 и 6 вместе с ребрами (4,5), (1, 3), (5, 7) и (3, 6). МОД изображено на рис. 1.1b, и его вес равен 14.
. Продолжая процесс, добавим последовательно вершины 5, 3, 7 и 6 вместе с ребрами (4,5), (1, 3), (5, 7) и (3, 6). МОД изображено на рис. 1.1b, и его вес равен 14.

