Графические возможности MatLab

Цель работ: Освоить технику работы с основными возможностями графики MatLab для отображения функций одного, двух и трех переменных и визуализации векторных и матричных данных. Работу, связанную с масштабированием осей и подбором цветов, MatLab берет на себя.

8.1. Диаграммы и гистограммы. Наглядным способом представления векторных и матричных данных явля­ются диаграммы и гистограммы. Значение элемента вектора пропорцио­нально высоте столбика диаграммы (в случае столбчатой диаграммы) или площади сектора диаграммы (для круговой диаграммы). Гистограммы ис­пользуются для получения информации о распределении данных по задан­ным интервалам.

8.1.1. Диаграммы векторных данных. Отображение вектора в виде столбчатой диаграммы осуществляется функци­ей bar.

 

Запишите, например вектор-строку

х = [1.2 1.7 2.2 2.4 2.5 1.3 1.1 0.5 0.4 0.l]

в переменную data и представьте ее столбчатой диаграммой, вызвав функ­цию bar с аргументом х:

» х = [1.2 1.7 2.2 2.4 2.5 1.3 1.1 0.5 0.4 0.1];

» bar(х)

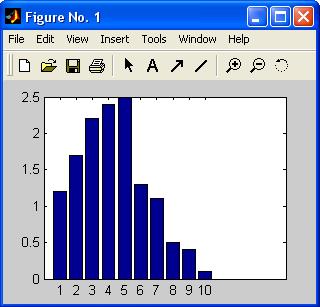
Рис. 3.

 

На экране появится графическое окно, изображенное на рис. 3, содержа­щее столбчатую диаграмму вектор-строки. По горизонтальной оси откладывается номер элемента вектора, а по вертикальной – его значение. Аргументом функции bar может быть как вектор-строка, так и вектор-столбец.

Разметку горизонтальной оси можно задать вектором с возрастающими зна­чениями. В этом случае первый аргумент bar является вектором с координа­тами точек разметки, а второй – вектором значений, которые требуется отобразить на диаграмме. Удобно использовать этот способ построения диаграммы для отображения значений элементов векторов в зависимости не от их номера, а например от времени, если в вектор записаны результаты измерений в некоторые моменты времени. Важно, чтобы длины этих векто­ров совпадали, иначе будет выдано сообщение об ошибке.

» time = [0.0 0.1 0.2 0.4 0.5 0.8 1.1 1.3];

» data = [2.85 2.93 2.99 3.26 3.01 2.25 2.09 1.79];

» bar(time, data)

Результат приведен на рис. 4. Пропущенные столбики соответствуют тем моментам времени, в которые измерения не производились.

Выбор ширины столбцов осуществляется заданием третьего дополнитель­ного аргумента. По умолчанию ширина равна 0.8. Диаграмма без промежут­ков между столбиками получается, если установить ширину, равную едини­це. Выбор значений, больших единицы, приводит к перекрывающимся столбикам. В качестве примера отобразите функцию x (t) =sint · e^t на отрезке

[–1, 1] в виде столбчатой диаграммы без промежутков, выполнив следую­щую последовательность операций:

» t=[–l:0.1:l];

» x=sin(t).*exp(t);

» bar(t,x,1.0)

Рис. 4.

 

Функция barh строит горизонтальную столбчатую диаграмму, т. е. повернутую на девяносто градусов. Для построения объемных диаграмм применяется функция bar3. Использование barh и bar3 аналогично bar.

Если требуется оценить вклад каждого из элементов вектора в общую сумму его элементов, то удобно построить круговую диаграмму при помощи функ­ции pie, например:

» data = [19.5 13.4 42.6 7.9];

» pie(data)

В результате получается диаграмма, изображенная на рис. 5, в кото­рой площади секторов отвечают процентному вкладу каждого из элемен­тов вектора в общую сумму, т. е. MatLab нормируетзначения, вычисляя data/sum(data).

Если сумма элементов вектора (аргумента pie) больше или равна единице, то MatLab производит нормировку и строит круг, состоящий из секторов. Если сумма меньше единицы, то нормировка не производится и получается круг с пропущенным сектором.

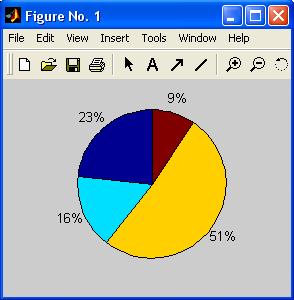
Рис. 5.

 

Часто необходимо отодвинуть от круга диаграммы сектор, соответствующий некоторому элементу. Это можно проделать, задав вторым аргументом функции pie вектор, состоящий из единиц и нулей, причем единица стоит в позиции, соответствующей номеру отделяемой части. Диаграмма с отделен­ным сектором (см. рис. 6), отвечающим значению 8.4, выводится в ре­зультате выполнения команд

» data = [19.5 13.4 42.6 7.9];

» parts = [0 1 0 0];

» pie(data, parts)

Можно отделить несколько секторов, расположив единицы во вспомога­тельном векторе на подходящих позициях. Важно только, чтобы размеры векторов были одинаковы.

В качестве упражнения напишите команды построения диаграммы с отде­ленным сектором, соответствующим максимальному значению среди эле­ментов вектора. Используйте функции zeros для создания нулевого вектора, той же длины, что х, и max с двумя выходными аргументами для поиска номера максимального элемента в векторе х. Ниже приведена требуемая последовательность команд:

» parts = zeros(size(data));

» [mx, ind] = max(data);

» parts(ind) = 1;

»pie(data, parts)

Рис. 6.

 

Визуализация векторных данных может быть осуществлена при помощи pie3 и bar3, которые строят трехмерные круговые и столбчатые диаграммы, например команды

» data = [24.1 17.4 10.9];

» parts =[1 0 0];

» pie3(data, parts)

приводят к появлению трехмерной круговой диаграммы с отделенным сек­тором, изображенной на рис. 7.

8.1.2. Гистограммы векторных данных. Обработка данных включает вопрос о том, сколько данных попало в тот или иной интервал. Для получения наглядного представления о распределении данных служит функция hist. Например, команды

» data = randn(100000, 1);

» hist(data)

заполняют вектор х числами, распределенными по нормальному закону, разбивают интервал, которому они принадлежат, на десять равных частей (по умолчанию) и строят гистограмму попадания чисел в каждый из интер­валов. Получающаяся гистограмма приведена на рис. 8.

Обратите внимание на масштаб вертикальной оси. Число 10⁴ в левом верхнем углу значит, что значения по вертикальной оси умножаются на 10 000, т. е. по вертикальной оси отложены числа 5000, 10 000, 15 000 и т. д.

 

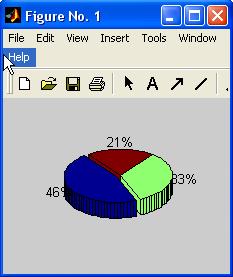
Рис. 7.

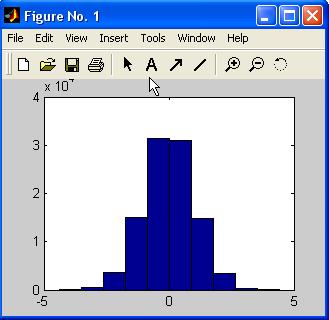
Рис. 8.

 

Для увеличения числа интервалов следует в качестве второго аргумента ука­зать число интервалов, например hist (data, 50). Вместо автоматического разбиения на равные интервалы можно использовать собственное, задав вторым аргументом вектор, содержащий центры интервалов. Команды

» data = [0.9 1.0 1.1 1.2 1.4 2.4 3.0 3.3];

» centers = [1.1 2.3 3.2];

» hist(data, centers)

приводят к построению диаграммы, изображенной на рис. 9, где звездочки на горизонтальной оси отмечают центры интервалов.

Часто необходимо задать не центры, а границы интервалов. Для построения таких гистограмм следует использовать функцию histc в сочетании с выше­описанной функцией bar. Функция histc возвращает вектор, содержащий число величин, попавших в заданные интервалы. При помощи функции bar с дополнительным аргументом 'histc' полученный вектор представляется в виде гистограммы.

» data = [0.9 1.0 1.1 1.2 1.4 2.4 3.0 3.3];

» interval = [1.1 2.0 3.2];

» count = histc(x, interval)

count =

3 2 0

» bar(interval, count, 'histc')

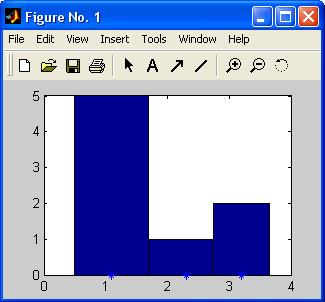
Рис. 9.

 

Функцию hist можно вызывать с одним или двумя выходными аргументами для получения массивов с информацией о распределении данных, при этом гистограмма не строится. В случае одного аргумента в него записывается вектор, содержащий распределение данных по интервалам.

Следующий пример демонстрирует создание вектора count из пяти элементов, каждый из которых соответствует числу элементов из data, попавших в один из пя­ти интервалов.

» data = randn(10000, 1);

» count = hist(data, 5)

Использование hist с двумя аргументами приводит к получению дополни­тельного вектора с информацией о расположении интервалов:

» [count, intervals] = hist(data, 5)

8.2. Представление матричных данных. Предположим, что в матрице DATA,состоящей из четырех строк и трех столбцов содержатся результаты измерений трех величин за четыре момента времени. Для построения столбчатой диаграммы данных примените функ­цию bar, задав в качестве аргумента массив DATA:

» DATA = [1.2 1.4 1.1

3.7 3.5 3.1

2.0 2.8 2.2

4.2 4.7 4.1];

» bar(DATA)

В результате появляется диаграмма сгруппированных данных, изображенная на рис. 10. На диаграмме расположены четыре группы данных, каждая из которых состоит из трех столбиков, соответствующих измеряемым величинам.

Использование аргументов функции bar для визуализации матричных дан­ных не отличается от случая векторных данных, разобранного в предыдущем разделе.

Ширина интервалов между столбцами внутри группы задается при помощи числового параметра. Диаграмма с перекрывающими­ся столбцами внутри группы получается при по­мощи bar (DATA,1.7).

Рис. 10.

 

Вклад каждой из величин в общую сумму внутри группы хорошо виден на диаграмме с накоплением, в которой каждая группа отображается в виде столбика, состоящего из частей. Число частей равно числу измеряемых ве­личин, а их высота соответствует вкладу каждой величины в сумму внутри группы. На рис. 11 показана диаграмма с накоплением, построенная при помощи функции bar с дополнительным аргументом: bar (DATA, ' stack').

Рис. 11.

 

Использование функции barh в случае матриц осуществляется так же, как и применение функции bar. Наглядная трехмерная столбцевая диаграмма, пред­ставляющая матричные данные, получается, если применить функцию bar3.

Проследить за изменением величин и одновременно узнать вклад значений в общую сумму позволяет функция area, выводящая диаграмму с областями. Запишите в матрицу GAINпоквартальную прибыль от продаж трех видов продукции и проследите за изменением прибыли при помощи диаграммы с областями (см. рис. 12).

» GAIN = [12.0 23.0 48.0

10.6 31.5 49.0

8.0 25.0 78.0

9.6 29.0 61.5];

» area(GAIN)

Дополнительные возможности для визуализации разреженных матриц и пред­ставлении матриц в виде изображений предоставляют функции spy и imagesc.

8.3. Графики функций. MatLab предоставляет обширные возможности для визуализации функций одной и двух переменных. Использование функций для построения графи­ков с минимальным набором задаваемых параметров (остальные MatLab вы­бирает автоматически) приводит к получению качественных графиков.

8.3.1. Графики функций одной переменной. MatLab позволяет строить графики функций в линейном, логарифмическом и полулогарифмическом масштабах. Причем в одном окне можно построить графики нескольких функций, даже определенных на разных отрезках.

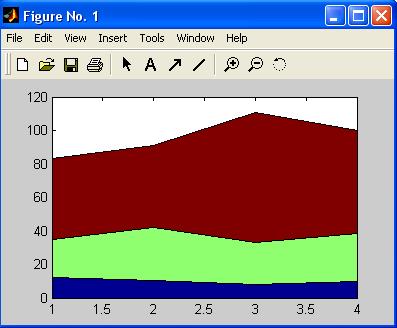
Рис. 12.

 

8.3.1.1. Графики в линейном масштабе. Построение графиков функций одной переменной в линейном масштабе осуществляется при помощи функции plot. В зависимости от входных ар­гументов функция plot позволяет строить один или несколько графиков, изменять цвет и стиль линий и добавлять маркеры на каждый график. Во второй главе приведен пример вывода простейшего графика функции одной переменной:

» х=[0:0.05:1];

» у = ехр(–х).*sin(10*x);

» plot(x, у)

Сравнение нескольких функций легко производить, построив графики на одних координатных осях. Постройте графики функций f (x)= e ^{–0,1 х} sin² х и

g (x) = e ^{–0,2 х} sin² х на отрезке [–2π, 2π].Сгенерируйте вектор-строку значений аргумента х и вектор-строк f и g,содержащих значения функций. Команда plot с двумя парами аргументов приводит к построению графика, изобра­женного на рис. 13.

» х = [-2*pi:pi/20:2*pi];

» f = exp(–0.1*x).*sin(x).^{^}2;

» g = ехр(–0.2*х).*sin(x).^{^}2;

» plot (x, f, x, g)

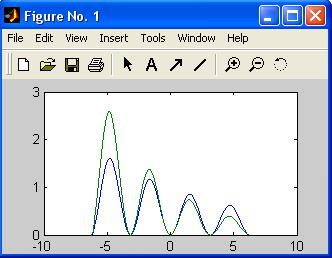
Рис. 13.

 

Функции необязательно должны быть определены на одном и том же отрез­ке. В этом случае при построении графиков MatLab выбирает максималь­ный отрезок, содержащий остальные. Важно только в каждой паре векторов абсцисс и ординат указать соответствующие друг другу вектора, например:

» xl = [–pi:0.01:2*pi];

» f = exp(–0.1*xl).*sin(xl).^{^}2;

» х2 = [–2*pi:0.01:pi];

» g = ехр(–0.2*х2).*sin(x2).^{^}2;.

» plot(xl, f, x2,g)

Аналогичным образом при помощи задания в plot через запятую пар аргу­ментов вида: вектор абсцисс, вектор ординат, осуществляется построение графиков произвольного числа функций.

Использование plot с одним аргументом – вектором – приводит к построе­нию "графика вектора", т. е. зависимости значений элементов вектора от их номеров. Аргументом plot может быть и матрица, в этом случае на одни коор­динатные оси выводятся графики столбцов.

Иногда требуется сравнить поведение двух функций, значения которых сильно отличаются друг от друга. График функции с небольшими значе­ниями практически сливается с осью абсцисс, и установить его вид не уда­ется. В этой ситуации помогает функция plotyy, которая выводит графики в окно с двумя вертикальными осями, имеющими подходящий масштаб.

Сравните, например, две функции: f(x)=x³ и F(x) = 1000*(x + 0.5)^–4.

» х = [0.5:0.01:3];

» f = х.^{^}–3;

» F = 1000*(х+0.5).^{^}–4;

» plotyy(х, f,x, F)

При выполнении этого примера обратите внимание, что цвет графика совпадает с цветом соответствующей ему оси ординат. Функция plot использует линейный масштаб по обеим координатным осям. Однако MatLab предоставляет пользователю возможность строить графики функций одной переменной в логарифмическом или полулогарифмическом масштабе.

8.3.1.2. Графики в логарифмических масштабах. Для построения графиков в логарифмическом и полулогарифмическом масштабах служат следующие функции:

- loglog (логарифмический масштаб по обеим осям);

- semilogx (логарифмический масштаб только по оси абсцисс);

- semilogy (логарифмический масштаб только по оси ординат).

Аргументы loglog, semilogx и semilogy задаются в виде пары векторов зна­чений абсцисс и ординат так же, как для функции plot. Постройте, например, графики функций f(x) = ln 0.5 x и g(x) = sin ln x на отрезке [0.1, 5] в логарифмическом масштабе по оси х:

» х = [0.1:0.01:10];

» f = log(0.5*x);

» g = sin(log(x));

» semilogx(x, f, x,g)

Аналогичным образом строятся графики при помощи функций loglog и

semilogy.

8.4. Оформление графиков. Удобство использования графиков во многом зависит от дополнительных элементов оформления: координатной сетки, подписей к осям, заголовка и легенды. Сетка наносится командой grid on, подписи к осям размещаются при помощи xlabel, ylabel, заголовок дается командой title. Наличие не­скольких графиков на одних осях требует помещения легенды командой legend с информацией о линиях. Все перечисленные команды применимы к графикам как в линейном, так и в логарифмическом и полулогарифмиче­ском масштабах. Следующие команды выводят графики изменения суточ­ной температуры, которые снабжены всей необ­ходимой информацией.

» time = [0 4 7 9 10 11 12 13 13.5 14 14.5 15 16 17 18 20 22];

» temp1 = [14 15 14 16 18 17 20 22 24 28 25 20 16 13 13 14 13];

» temp2 = [12 13 13 14 16 18 20 20 23 25 25 20 16 12 12 11 10];

» plot(time, temp1, 'ro-', time, temp2, 'go-')

» grid on

» title(' Суточные температуры ')

» xlabel(' Время (час.) ')

» ylabel(' Температура (С) ')

» legend(' 10 мая ', ' 11 мая ')

При добавлении легенды следует учесть, что порядок и количество аргумен­тов команды legend должны соответствовать линиям на графике. Последним дополнительным аргументом legend может быть положение легенды в графическом окне:

– 1 – вне графика в правом верхнем углу графического окна;

0 – выбирается лучшее положение в пределах графика так, чтобы как
можно меньше перекрывать сами графики;

1 – в верхнем правом углу графика (это положение используется по
умолчанию);

2 – в верхнем левом углу графика;

3 – в нижнем левом углу графика;

4 – в верхнем левом углу графика.

В заголовке графика, легенде и подписях осей допускается добавление фор­мул и изменение стилей шрифта при помощи формата ТеХ.

8.5. Графики параметрических и кусочно-заданных функций. Для построения функций, заданных параметрически, следует сперва сгенериро­вать вектор значений аргумента. Затем необходимо вычислить значения функ­ций и записать их в векторы, которые и надо использовать в качестве аргу­ментов plot. График функции x (t)=0.5·sin t, y (t) =0.1· cost для t =[0,2π] (эллипс), получается при помощи следующих команд:

» t = [0:0.01:2*pi];

» х = 0.5*sin(t);

» у = 0.7*cos(t);

» plot(x, y)

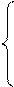Для того чтобы проверить свои знания о построении графиков и работе с массивами, постройте график функции, заданной кусочным образом:

π·sin x, –2·π ≤ x ≤–π;

y (x) = π – │ x │, –π ≤ x ≤ –π;

π·sin³ x, π ≤ x ≤ 2·π;

Сначала необходимо вычислить каждую из трех ветвей, т. е. фактически по­лучить три пары массивов x 1 и y 1, х 2 и у 2, х 3 и у 3, затем объединить зна­чения абсцисс в вектор х, а значения ординат в у и построить график функ­ции, задаваемой парой массивов х и у:

» xl = [–2*pi:0.01:–pi];

» yl = pi*sin(xl);

» х2 = [–pi:0.01:pi];

» у 2 = pi–abs(x2);

» хЗ = [pi:0.01:2*pi];

» уЗ = pi*sin(xl).^3;

» х = [xl х2 хЗ];

» У = [yl у2 уЗ];

» plot(х, у)

Можно поступить и по-другому – построить графики трех ветвей, как три различные функции:

» plot(xl, yl, х2, у2, хЗ, уЗ)

В этом случае график имеет более наглядный вид, т. к. каждая ветвь функ­ции строится своим цветом.

8.6. Анимированные графики. При изучении движения точки на плоскости или в трехмерном пространст­ве полезно не только построить траекторию точки, но и следить за движением точки по траектории. MatLab предоставляет возможность получить анимированный график, на котором кружок, обозначающий точку, переме­щается на плоскости или в пространстве, оставляя за собой след в виде ли­нии – траектории движения. График похож на летящую комету с хвостом. Для построения анимированных графиков применяются функции comet и comet3. Постройте, например, траекторию движения точки в течение 10 секунд, координаты которой изменяются по закону: x (t) = sin t /(t + 1) y (t) = cos t /(t + 1).

Действуйте точно так же, как при построении графика параметрически за­данной функции, но для визуализации результата используйте commet:

» t = [0:0.001:10];

» х = sin(t)./(t+l);

» у = cos(t)./(t+l);

» comet (x, y)

При выполнении последней команды следите за тем, чтобы окно с графи­ком было поверх остальных окон. Скоростью движения кружка можно управлять, задавая различные шаги при автоматическом заполнении вектора, соответствующего времени. Использо­вание comet с одним аргументом (вектором) приводит к построению дина­мически рисующегося графика значений элементов номера в зависимости от их номеров. Функцию comet можно вызвать и с третьим дополнительным числовым параметром, который задает длину хвоста кометы. По умолчанию он равен 0.1. Обратите внимание, что при изменении размеров графиче­ского окна или при его минимизации и последующем восстановлении тра­ектория движения пропадает. Это связано со способом, который применяет MatLab для построения графика.

Получите самостоятельно траекторию движения фиксированной точки на окружности, катящейся по прямой (циклоиду). Циклоида описывается па­раметрическими зависимостями x (t) = t – sint, y (t) = 1 – cost.

Для построения траектории точки, перемещающейся в пространстве, ис­пользуется функция comet3.

8.7. Работа с несколькими графиками. Во всех примерах, приведенных в предыдущей лабораторной работе, графики выводи­лись в специальное графическое окно с заголовком Figure No. 1. При сле­дующем построении графика предыдущий график пропадал, а новый выводился в то же самое окно. MatLab предоставляет следующие возможности работы с несколькими графиками:

- вывод каждого графика в свое окно;

- вывод нескольких графиков в одно окно (на одни координатные оси);

- отображение в пределах одного окна нескольких графиков, каждого на своих осях.

8.7.1. Вывод графиков в отдельные окна. Команда figure, определенная в MatLab, служит для создания пустого гра­фического окна и отображения его на экране. Окно становится текущим,т. е. все последующие графические функции будут осуществлять построение графиков в этом окне. Для получения нового графического окна следует снова использовать figure. Например, последовательность команд

» [X, Y] = meshgrid(–1:0.1:1, 0:0.1:1);

» Z = 4*sin(2*pi*X).*cos(1.5*pi*Y).*(1–Х.^2).*Y.*(1–Y);

» figure

» mesh(X, Y, Z)

» figure

» surfl(X, Y, Z)

приводит к появлению на экране двух фафических окон: Figure No. 1, со­держащего каркасную поверхность, и Figure No. 2 с освещенной поверхно­стью. Окно Figure No. 2 является текущим, т. к. было создано последним. Команды, набираемые далее, например

» colormap('copper')

приведут к изменениям именно в этом окне. Для того чтобы сделать графическое окно Figure No. 1 текущим, следует щелкнуть на нем мышкой, вер­нуться в рабочую среду MatLab и продолжать ввод команд. Команды повле­кут изменения в окне Figure No. 1. Для очистки всего текущего окна используется команда сlf (сокращение от clear figure), а для того, чтобы уб­рать только график, но оставить оси, заголовок и названия осей, следует применить cla (сокращение от clear axes).

Вышеописанным способом можно получить сколько угодно графических окон и вывести в них графики различных функций или визуализировать векторные и матричные данные. Однако для изменения того или иного графика придется искать его окно на экране и делать его текущим при помощи щелчка мыши. Есть более универсальный и удобный способ работы с не­сколькими окнами. При создании каждого нового графического окна при помощи figure следует вызвать ее с выходным аргументом. Этот аргумент называется в MatLab указателемна графическое окно. Значением выходного аргумента является число, совпадающее с номером графического окна. Для того чтобы сделать графическое окно текущим, следует вызвать figure, применив в качестве входного аргумента указатель на требуемое графиче­ское окно. Разберите использование указателей на следующем примере. Требуется создать два графических окна, построить в них графики функций f = sin x и g = ln x,а затем оформить их – дать заголовки и нанести сетку на второй график. Последовательность команд, приведенная ниже, позволяет получить желаемый результат.

» sinGr = figure;

» lnGr = figure;

» x = [0.1:0.05:10];

» f = sin(x);

» g = log (x);

» figure(sinGr)

» plot (x, f)

» figure(lnGr)

» plot (x, g)

» figure(sinGr)

» title (' \itf=sin\itx ')

» figure(lnGr)

» title('\itg=ln\itx')

» grid on

Для того чтобы очистить графическое окно с указателем lnGr, следует ис­пользовать команду сlf (lnGr).Удаление графика из первого окна, на кото­рое указывает sinGr, производится при помощи команды cla (sinGr).

8.7.2. Вывод нескольких графиков на одни оси. Возможность отображения нескольких графиков функций одной перемен­ной на одних осях использовалась при изучении функций plot, plotyy, semilogx, semilogy, loglog. Они позволяют выводить графики нескольких функций, задавая соответствующие векторные аргументы парами, например plot (x,f,x,g). Однако, при построении трехмерных графиков или различных типов графиков, объединять их на одних осях не было возможности. Для объединения графиков предназначена команда hold on, которую нужно задать перед построением следующего графика. В следующем примере вы­водится пересечение плоскости и конуса, заданного параметрически.

» u = [–2*pi:0.1*pi:2*pi]';

» v = [–2*pi:0.1*pi:2*pi]

»X = 0.3*u*cos(v);

» Y = 0.3*u*sin(v);

» Z = 0.6*u*ones(size(v));

» surf(X, Y, Z)

» [X, Y] = meshgrid(–2:0.1:2);

» Z = 0.5*X+0.4*Y;

» hold on

» mesh(X, Y, Z)

» hidden off

Команда hidden off применена для того, чтобы показать часть конуса, на­ходящуюся под плоскостью. Обратите внимание, что hold on распространяется на все последующие вы­воды графиков в текущее окно. Для размещения графиков в новых окнах следует выполнить команду hold off. Команда hold on может применяться и для расположения нескольких графиков функций одной переменной, на­пример,

» plot (x, f, х, g)

эквивалентно последовательности

» plot(х, f)

» hold on

» plot (x, g)

8.7.3. Несколько графиков в одном графическом окне. MatLab позволяет разбить графическое окно на несколько подграфиков со своими осями. Для этого служит команда subplot, которая располагает подграфики в виде матрицы и используется с тремя параметрами: subplot (i, j, n). Здесь i и j – число подграфиков по вертикали и горизон­тали, a n – номер подграфика, который надо сделать текущим. Номер отсчитывается от левого верхнего угла построчно. Например, команда subplot (3, 2, 4) предполагает наличие шести подграфиков и делает четвер­тый текущим. После выполнения subplot (3, 2, 4) все графические функции будут осуще­ствлять вывод именно в этот подграфик.