

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Интересное:
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Кроме математического ожидания и дисперсии, в теории вероятностей применяется еще ряд числовых характеристик, отражающих те или иные свойства распределения.
Модой Мо(Х) случайной величины Х называется ее наиболее вероятное значение (для которого вероятность pi или плотность вероятности φ (x) достигает максимума).
Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным (рис. 5.3)


Рис. 5.3 Рис. 5.4
Медианой Ме(Х) непрерывной случайной величины Х называется такое ее значение, для которого
 ,
,
т.е. вероятность того, что случайная величина Х примет значение, меньшее медианы Ме(Х) или большее ее, одна и та же и равна 1/2. Геометрически вертикальная прямая x =Ме(Х), проходящая через точку с абсциссой, равной Ме(Х), делит площадь фигуры под кривой функции распределения на две равные части (см. рис. 5.4). очевидно, что в точке x =Ме(Х) функция распределения равна 1/2, т.е. F(Ме(Х))= 1/2 (рис. 5.5).

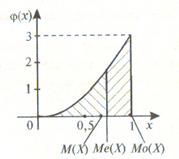
Рис. 5.5 Рис. 5.6
Пример 5.2.13. Найти моду, медиану и математическое ожидание случайной величины Х с плотностью вероятности  при x Î[0; 1].
при x Î[0; 1].
○ Кривая распределения представлена на рис. 5.6. Очевидно, что плотность вероятности  максимальна при x =Мо(Х)=1.
максимальна при x =Мо(Х)=1.
Медиану Ме(Х)= b найдем из условия
 , т.е.
, т.е.  или
или
 , откуда
, откуда
 .
.
 .
.
Взаимное расположение точек М(Х), Ме(Х) и Мо(Х) в порядке возрастания абсцисс показано на рис. 5.6. ●
Квантилем уровня q (или q -квантилем) называется такое значение xq случайной величины Х, при котором функция ее распределения принимает значение, равное q, т.е.
F(xq)=P(X< xq)= q.
Некоторые квантили получили особое название. Очевидно, что медиана случайной величины есть квантиль уровня 0,5, т.е. Ме(Х)= x 0,5. Квантили x 0,25 и x 0,75 получили название соответственно верхнего и нижнего квантилей[1].
|
|
С понятием квантиля тесно связано понятие процентной точки. Под 100%-ной точкой подразумевается квантиль x 1- q, т.е. такое значение случайной величины Х, при котором P(X³ x 1- q)= q.
Пример 5.2.14. По данным примера 5.2.13. найти квантиль x 0,3 и 30%-ную точку случайной величины Х.
○
Найдем F(x):
 .
.
Квантиль x 0,3 найдем из уравнения F(xq)= q, т.е.  , откуда
, откуда  .
.
Найдем 30%-ную точку случайной величины Х, или квантиль x 0,7, из уравнения  , откуда
, откуда  .●
.●
Начальный и центральный моменты k-го порядка для непрерывной случайной величины определяются также как и для дискретной (см. 5.2.2.5).
| Момент | Случайная величина | |
| Дискретная | Непрерывная | |
| Начальный | 
| 
|
| Центральный | 
| 
|
Отметим, что математическое ожидание М(Х), или первый начальный момент ν 1, характеризует среднее значение или положение распределения случайной величины Х на числовой оси; дисперсия D(X), или второй центральный момент m 2, – степень рассеяния распределения Х относительно М(Х). для более подробного описания распределения служат моменты высших порядков.
Третий центральный момент m 3 служит для характеристики асимметрии (скошенности) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на  , где
, где  – среднее квадратическое отклонение случайной величины Х. Полученная величина называется коэффициентом асимметрии случайной величины:
– среднее квадратическое отклонение случайной величины Х. Полученная величина называется коэффициентом асимметрии случайной величины:
 .
.
Если распределение симметрично относительно математического ожидания, то коэффициент асимметрии А =0.


Рис. 5.7 Рис. 5.8
На рисунке 5.7 показаны две кривые распределения: I и II. Кривая I имеет положительную (правостороннюю) асимметрию (А>0), а кривая II – отрицательную (левостороннюю) (А<0).
Четвертый центральный момент m 4 служит для характеристики крутости (островершинности или плосковершинности) распределения.
Эксцессом (или коэффициентом эксцесса) случайной величины называется число
|
|
 .
.
Число 3 вычитается из отношения  потому, что для наиболее часто встречающегося нормального распределения (о нем речь пойдет в 5.2.4.5) отношение
потому, что для наиболее часто встречающегося нормального распределения (о нем речь пойдет в 5.2.4.5) отношение  . Кривые, более островершинные, чем нормальная, обладают положительным эксцессом, более плосковершинные – отрицательным эксцессом (рис. 5.8).
. Кривые, более островершинные, чем нормальная, обладают положительным эксцессом, более плосковершинные – отрицательным эксцессом (рис. 5.8).
 Пример 5.2.15. Найти коэффициент асимметрии и эксцесс случайной величины, распределенной оп так называемому закону Лапласа с плотностью вероятности
Пример 5.2.15. Найти коэффициент асимметрии и эксцесс случайной величины, распределенной оп так называемому закону Лапласа с плотностью вероятности  .
.
○Так как распределение случайной величины Х симметрично относительно оси ординат (рис. 5.9), то все нечетные как начальные, так и центральные моменты равны 0, т.е. ν 1=0, ν 3=0, m 3=0. Тогда коэффициент асимметрии  .
.
Для нахождения эксцесса необходимо вычислить четные начальные моменты ν 2 и ν 4:


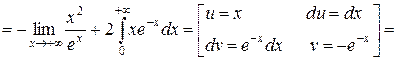


Следовательно,
D(X)= m 2=  и
и 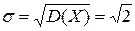 .
.
 , тогда
, тогда
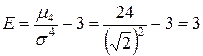 .
.
Эксцесс распределения положителен, что говорит об островершинности кривой распределения  (рис. 5.9).●
(рис. 5.9).●
|
|
|

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!