Внедрение организационного проекта проводится на основании материалов по реализации рабочего проекта организации производства, содержащихся в комплекте рабочей документации, в два этапа.:
· подготовка к внедрению;
· внедрение.
Этап внедрениявключает три вида работ: реализация организационного проекта; расчет фактического экономического эффекта; проведение приемо-сдаточных работ.
В реализации проекта совершенствования или преобразования организации производства на предприятии в отличие от внедрения проекта построения новой организационной системы можно выделить три части:
1) частичное внедрение, когда элементы проектируемой организации производства постепенно вытесняют элементы функционирующей системы и поэтому существуют рядом с ними;
2) полное внедрение, знаменующееся заменой старой системы на проектируемую;
3) адаптация новой системы, доказывающая ее жизнеспособность и эффективность.
10. Модели ценообразования на рынке капиталов: САРМ, АРТ, Фамы-Френча, Блэка, Дженсона
Модель оценки CAPM была разработана экономистом, а впоследствии лауреатом Нобелевской премии по экономике Уильямом Шарпом и изложена в его книге 1970 года «Портфельная теория и рынки капитала». Его идея начинается с того, что отдельные инвестиции включают два вида рисков:
- Систематические. Это рыночные риски, которые не могут быть диверсифицированы. Их примерами являются процентные ставки, спады и войны.
- Несистематические. Также известны как специфические. Они специфичны для отдельных акций и могут быть диверсифицированы увеличением количества ценных бумаг в инвестиционном портфеле. Говоря техническим языком, они представляют собой компонент биржевой прибыли, который не коррелирует с общими движениями рынка.
Современная портфельная теория говорит о том, что специфический риск может быть устранен с помощью диверсификации. Проблема заключается в том, что она по-прежнему не решает проблему систематического риска. Даже портфель, состоящий из всех акций фондового рынка, не может устранить его. Поэтому при расчете справедливого дохода систематический риск больше всего досаждает инвесторам. Данный метод является способом его измерить.
Портфель М, включающий все существующие активы и структурно копирующий рынок, называется рыночным. Очевидно, что его ожидаемая доходность Rm и риск σМ будут соответствовать среднерыночным значениям.
Также предположим, что на рынке существует некоторый безрисковый актив F, например, ценные бумаги, эмитированные государством. Тогда формула САРМ имеет вид:
 i =Rf+ βi(
i =Rf+ βi( m - Rf), где Rf – безрисковая ставка, βi – бета-величина ценной бумаги (отношение ее риска к риску на рынке в целом –количественная мера систематического риска), Rm – ожидаемая доходность, (Rm - Rf) – премия за риск.
m - Rf), где Rf – безрисковая ставка, βi – бета-величина ценной бумаги (отношение ее риска к риску на рынке в целом –количественная мера систематического риска), Rm – ожидаемая доходность, (Rm - Rf) – премия за риск.
βi=1 – средняя степень риска, сложившаяся на рынке ценных бумаг
βi<1 – актив менее рисковый по сравнению с рынком
βi>1 – актив более рисковый по сравнению с рынком
Теория арбитражного ценообразования АРТ
Согласно этой теории доходность рисковых активов зависит от некоторого числа систематических факторов, а собственные риски не принимаются во внимание, т.к. поддаются диверсификации. В основе АРТ лежит фундаментальный закон единой цены, который гласит, что на совершенном рынке портфели или активы с одинаковым риском должны иметь одинаковую цену и соот-но доходность. Иначе возникает возможность арбитража- извлечения безрисковой прибыли за счет одновременной купли-продажи активов или портфелей по разным ценам на одном и том же рынках без вложений со стороны инвестора. Для этого нужно купить портфель по более низкой цене и тут же продать по более высокой. Заработанная при этом разница будет полож.величиной, поскольку позиции (купля- продажа) взаимно компенсируются. Проведение арбитражных операций в конечном счете приводит к восстановлению рыночного равновесия цен, и арбитраж выступает основным механизмом рыночного ценообразования.
Формула:
 i=Rf+ βin(
i=Rf+ βin( n - Rf),
n - Rf),
Где Rf – безрисковая доходность, βin - коэф, отраж.чувствительность актива i к изменениям фактора n; n – общее число факторов системат.риска,  n – Rf – премия за системат.риск по фактору n
n – Rf – премия за системат.риск по фактору n
Это основное уравнение модели АРТ, согласно которой активы или портфели с одинак. Чувствельностью к базовым факторам должны иметь одинак. ожидаемую дох-ть, иначе появляются возможности для арбитража. При этом каждый отд.фактор может оказывать как положит, так отриц. влияние на дох-ть актива.
В целом АРТ ближе к реальности, чем САРМ. Проведенные рядом заруб. исследователей тестирвоания АРТ показали, что она более адекватно по сравнению с САМР описывает процессы ценообразования на рынке капиталов.
Трехфакторная модель Фама-Френча (The Fama-French Three Factor Model) представляет собой очень полезный инструмент для понимания работы портфеля, для измерения воздействия активного управления, структуры портфеля и для оценки будущей прибыли. Трехфакторная модель заменяет САРМ в качестве общепринятого объяснения ценообразования акций и процесса получения прибыли инвестором. Модель Фамы и Френча говорит о том, что для оценки ожидаемой доходности актива не достаточно учитывать только доходность рыночного портфеля, а следует также учесть факторы rSMB и rHML.
Модель Фама и Френча выглядит так:

Модель оценки капитальных активов Ф.Блэка-CAPM с нулевым "бета"
Второй, менее известной версией модели CAPM является версия Ф. Блэка В отличие «классической» модели CAPM в версии Шарпа–Линтнера, модель CAPM в версии Блэка не подразумевает существования на рынке безрискового актива. Основной вывод модели, как и в «классической» версии, заключается в том, что ожидаемая доходность любого актива пропорциональна относительной рискованности этого актива, мерой которой является ковариация доходностей актива и любого из эффективных портфелей. Кардинальное отличие выводов модели Блэка состоит в том, что ожидаемая доходность произвольного актива может быть описана ожидаемой доходностью любого эффективного портфеля и доходностью некоторого гипотетического портфеля. Гипотетический ненаблюдаемый портфель, это так называемый актив с нулевым бета. Таким образом, актив с нулевым бета, по определению, это такая комбинация рискованных активов, доходность которой имеет нулевую ковариацию с данным эффективным портфелем и наименьший уровень риска.
Подчеркнем еще несколько важных отличий модели Ф. Блэка от «классической» версии CAPM:
1. – Ожидаемая доходность любого актива определяется линейной комбинацией ожидаемых доходностей двух ненаблюдаемых портфелей (по сути, эта модель является двухфакторной).
2. – Модель Блэка не требует, чтобы все инвесторы формировали одинаковые по структуре инвестиционные портфели. Разные инвесторы могут формировать инвестиционные портфели в соответствии со своими предпочтениями, используя разные эффективные портфели и, соответственно, разные активы с нулевым бета.
3. – Поскольку нет известной всем безрисковой ставки, то формирование индивидуального инвестиционного портфеля требует либо возможности коротких продаж, либо наличия активов с отрицательным бета–коэффициентом (отрицательной ковариацией доходности хотя бы одного актива с доходностью эффективного портфеля).
Эти отличия делают модель Блэка более реалистичной и гибкой, чем модель Шарпа-Линтнера, но и значительно более сложной для эконометрической проверки и применения.
Мера Дженсена. Дженсен подходил к исследованию результатов инвестиционной деятельности, оценивая превышения доходности портфеля ri,t над безрисковой доходностью rf,t в каждый момент рассматриваемого периода (в нашем случае - за последние три года). Мера Дженсена, обозначаемая Ji, есть не что иное, как свободный член в регрессионном уравнении, описывающем линейную регрессию превышения (ri,t - rf,t) рассматриваемого портфеля на превышения (rm,t - rf,t) рыночного портфеля:



 (3.1)
(3.1)
Мера Дженсена может быть вычислена двумя способами:
а) если определены средние значения 

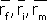
 и
и 


 , то:
, то:




б) в другом случае можно брать наблюдавшиеся значения ri,t, rf,t, rm,t положим, за каждый месяц предшествующих трех лет, вычислять превышения (ri,t -rf,t) и (rm,t -rf,t), подставлять их в регрессионную формулу (3.1) и вычислять Ji как свободный член регрессии. Возможность прямого вычисления меры Дженсена как свободного члена регрессии является одним из главных преимуществ метода Дженсена. Затем мера J i сравнивается с мерой Jm рыночного портфеля, которая равняется нулю.
Способность менеджера превысить показатели рыночного портфеля будет выражаться тем, что мера Ji станет больше нуля, а при неудачах менеджера мера станет отрицательной.





 i =Rf+ βi(
i =Rf+ βi(



 (3.1)
(3.1)

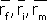
 и
и 


 , то:
, то:





