

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
Топ:
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Интересное:
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
ЭКЗАМЕНАЦИОННЫЕ БИЛЕТЫ ПО ФИЗИКЕ
Билет №1
1. Механическое движение. Относительность движения. Система отсчета. Материальная точка. Траектория. Путь и перемещение. Мгновенная скорость.
2. Лабораторная работа по теме «Измерение ускорения тела при равноускоренном движении».
Билет №2
1. Свободное падение тел. Равномерное движение по окружности. Центростремительное ускорение. Кинематика вращательного движения. Связь между угловой и линейной скоростью.
2. Задача по теме «Законы сохранения в механике».
Билет №3
1. Взаимодействие тел. Сила. Второй закон Ньютона.
2. Задача по теме «Импульс тела».
Билет №4
1. Импульс тела. Закон сохранения импульса. Проявление закона сохранения импульса в природе и его использование в технике.
2. Задача по теме «Кинематика вращательного движения».
Билет №5
1. Закон всемирного тяготения. Сила тяжести. Вес тела. Невесомость.
2. Задача на нахождение КПД теплового двигателя.
Билет №6
1. Энергия. Потенциальная и кинетическая энергия..
2. Задача по теме «Первый закон термодинамики. КПД тепловых двигателей».
Билет №7
1. Превращение энергии при механических колебаниях. Свободные и вынужденные колебания.
2. Задача на параллельное соединение проводников
Билет №8
1. Опытное основание основных положений МКТ строения вещества. Масса и размер молекул. Постоянная Авогадро.
2. Задача на движение или равновесие зараженной частицы в электрическом поле.
Билет №9
1. Идеальный газ. Основное уравнение МКТ идеального газа. Температура и ее измерение. Абсолютная температура.
2. Задача на определение индукции магнитного поля (по закону ампера или формулы для расчета силы Лоренца).
Билет №10
1. Работа силы. Мощность.
2. Задача по теме «Закон сохранения энергии»
Билет №11
1. Уравнение состояния идеального газа. Изопроцессы.
2. Задача по теме «Закон Кулона».
Билет №12
1. Испарение и конденсация. Насыщение и ненасыщенные пары. Влажность воздуха. Измерение влажности воздуха.
2. Лабораторная работа «Измерение сопротивления двух последовательно соединенных резисторов».
Билет №13
1. Кристаллические и амфорные тела. Упругие и пластические деформации твердых тел.
2. Задача на применение закона электромагнитной индукции.
Билет №14
1. Силы и энергия межмолекулярного взаимодействия. Строение газообразных, жидких и твёрдых тел. Опыт Штерна.
2. Задача по теме «Внутренняя энергия. Расчет количества теплоты».
|
|
Билет №15
1. Идеальный газ. Параметры состояния идеального газа
2. Лабораторная работа по теме «Определение модуля упругости материала»
Билет №16
1. Внутренняя энергия. Теплоёмкость. Удельная теплоёмкость. Первое начало термодинамики. Адиабатный процесс.
2. Задача на применение закона сохранения энергии.
Билет № 17
1. Электромагнитная индукция. Магнитный поток. Закон электромагнитной индукции. Правило Ленца
2. Задача на тему «Закон сохранения импульса».
Билет №18
1. Конденсаторы. Электроемкость конденсатора. Применение конденсаторов.
2. Задача на применение уравнения состояния идеального газа.
Билет №19
1. Работа и мощность в цепи постоянного тока. Электродвижущая сила. Закон Ома для полной цепи.
2. Лабораторная работа «Измерение массы тела».
Билет №20
1. Магнитное поле, условия его существования. Действие магнитного поля на электрический заряд и опыты, подтверждающие это действие. Магнитная индукция.
2. Лабораторная работа «Измерение влажности воздуха».
Билет №21
1. Полупроводники. Собственная и примесная проводимость полупроводников. Полупроводниковые приборы.
2. Задача на изопроцессы.
Билет №22
1. Принцип действия тепловой машины. КПД теплового двигателя.
2. Задача на определение работы газа с помощью графика зависимости давления газа от его объема.
Билет №23
1. Второе начало термодинамики. Холодильная машина. Тепловой двигатель.
2. Задача на применение закона сохранения импульса.
Билет №24
1. Свойства жидкостей. Поверхностный слой жидкости. Капиллярные явления.
2. Лабораторное работа по теме «Определение влажности воздуха в кабинете физики».
Билет №25
1. Свойства твёрдых тел. Закон Гука. Механические свойства твёрдых тел. Плавление и кристаллизация.
2. Задача на определение модуля Юнга материала, из которого изготовлена проволока.
Билет №26
1. Принцип суперпозиции полей. Работа сил электростатического поля. Потенциал. Разность потенциалов.
|
|
2. Задача на применение закона Джоуля-Ленца.
Приложение к экзаменационным билетам (задачи).
Билет №2
Билет №3
Билет №4
Билет №5
Билет №6
Билет №7
Билет №8
Билет №9
Задача на определение индукции магнитного поля (по закону ампера или формулы для расчета силы Лоренца).
Определите индукцию однородного магнитного поля, если на проводник длиной 0,2м со стороны поля действует сила 50 мН. Проводник образует угол 300 направлением силовых линий поля и по нему течет ток силой 10 А.
Билет №10
Билет №11
Билет №13
Билет №14
Билет №16
Билет №17
Билет №18
Билет №21
Задача на изопроцессы.
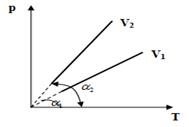
На рисунке представлены две изохоры для одной и той же массы идеального газа. Как определяется отношение объемов, занимаемых газами 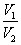 , если углы наклона изохор к оси абсцисс равны
, если углы наклона изохор к оси абсцисс равны  и
и 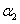 ?
?
Билет №22
Билет №23
Билет №25
Билет № 26
Эталоны правильных ответов
Билет№1
1. Механическое движение. Относительность движения. Система отсчета. Материальная точка. Траектория. Путь и перемещение. Мгновенная скорость.
Механическим движением называют изменение положения тела (или его частей) относительно других тел.
Из этих примеров видно, что всегда надо указать тело, относительно которого рассматривается движение, его называют телом отсчета. Система координат, тело отсчета, с которым она связана, и выбранный способ измерения времени образуют систему отсчета. Таким образом, иногда размерами тела по сравнению с расстоянием до него можно пренебречь, в этих случаях тело считают материальной точкой, Линию, вдоль которой движется материальная точка, называют траекторией. Длина части траектории между начальным и конечным положением точки называют путем (L). Единица измерения пути — 1м.
Механическое движение характеризуется тремя физическими величинами: перемещением, скоростью и ускорением.
Направленный отрезок прямой, проведенный из начального положения движущейся точки в ее конечное положение, называется перемещением (s).
Скорость — векторная физическая величина, характеризующая быстроту перемещения тела, численно равная отношению перемещения за малый промежуток времени к величине этого промежутка.
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло
Движение, при котором скорость тела не меняется, т. е. тело за любые равные промежутки времени перемещается на одну и ту же величину, называют равномерным прямолинейным движением.
При таком движении скорость и ускорение имеют одинаковые направления, причем скорость изменяется одинаково за любые равные промежутки времени. Этот вид движения называют равноускоренным.
|
|
При торможении автомобиля скорость уменьшается одинаково за любые равные промежутки времени, ускорение меньше нуля; так как скорость уменьшается, то уравнения принимают вид:
v = v0 + at, s = v0t - at2/ 2. Такое движение называют равнозамедленным.
Билет №2
Свободное падение тел. Равномерное движение по окружности. Центростремительное ускорение. Кинематика вращательного движения. Связь между угловой и линейной скоростью.
1. Одним из наиболее распространенных видов движения с постоянным ускорением - свободное падение тел.
Свободное падение - это движение тел только лишь под действием притяжения Земли (под действием силы тяжести).
При свободном падении все тела вблизи поверхности Земли независимо от их массы приобретают одинаковое ускорение, называемое ускорением свободного падения.
Условное обозначение ускорения свободного падения - g.
На поверхности Земли ускорение свободного падения (g) меняется в пределах от 9,78 м/с2 на экваторе до 9,83 м/с2 на полюсе.
2. Движение по окружности - частный случай криволинейного движения.
Если за любые равные промежутки времени радиус-вектор тела поворачивается на одинаковые углы, а линейная скорость тела по модулю не изменяется (т. е. если |v0|=|v|), движение тела по окружности называют равномерным (не следует забывать, что равномерное движение по окружности происходит с ускорением, так как скорость тела непрерывно меняется по направлению).
Угловой скоростью называют величину, равную отношению угла поворота радиуса-вектора точки, движущейся по окружности к промежутку времени t, в течение которого произошел этот поворот.
Скорость тела, направленную по касательной к окружности, называют линейной.
Мгновенная скорость тела в каждой точке криволинейной траектории направлена по касательной к траектории. Следовательно, в криволинейном движении направление скорости тела непрерывно изменяется. т.е. движение по окружности со скоростью, постоянной по модулю является ускоренным. Центростремительное ускорение всегда направлено к центру окружности: 
Линейная и угловая скорости связаны между собой:  , т.е.
, т.е.  .
.
Период - физическая величина, показывающая, чему равно время, за которое точка совершает один полный оборот. Если обозначить N – число оборотов, а Т – период, то:  .
.
Единица измерения в СИ – с. Т.к. за период точка поворачивается на угол 2π, то 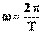 .
.
Частота – количество оборотов, которое совершила точка за единицу времени:  .
.
Единица измерения в СИ – Гц (герц). Частота равна одному герцу, если за 1 секунду точка совершает один полный оборот (1Гц=1с-1). Частота и период – взаимно обратные величины: 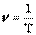 . Следовательно:
. Следовательно:  .
.
|
|
Билет№3
Сила. Масса. Второй закон Ньютона.
Действия тел друг на друга, создающие ускорение, называются силами. Все силы можно разделить на два основных типа: силы, действующие при непосредственном соприкосновении, и силы, которые действуют независимо от того, соприкасаются тела или нет, т. е. на расстоянии.
Сила - векторная величина. Силу измеряют динамометром. Силы, действующие при непосредственном соприкосновении, действуют по всей соприкасающейся поверхности тел. Молоток, ударяющий по шляпке гвоздя, действует на всю шляпку. Но если площадь мала, то считают, тело действует на одну точку. Эта точка называется точкой приложения. Если же на тело действует несколько сил, то их действие на тело можно заменить одной заменяющую силу называют суммой или равнодействующей.
Свойство тел приобретать определенное ускорение при данном воздействии называется инертностью. Инертность состоит в том, что для изменения скорости тела на заданную величину нужно, чтобы на него действовало другое тело и это действие длилось некоторое время. Инертность - это свойство, присущее всем телам. Масса тела — количественная мера его инертности.
О теле, которое в результате взаимодействия меньше изменяет свою скорость, говорят, что оно более инертно, масса его больше:

В СИ единицей массы тела является килограмм (кг).
Так как масса входит в закон всемирного тяготения, то она определяет также гравитационное взаимодействие тел.
II закон Ньютона
Сила, действующая на тело, равна произведению массы тела на создаваемое этой силой ускорение, причем направления силы и ускорения совпадают: а =F/m
Закон можно выразить в другой форме. Ускорение, сообщаемое телу, прямо пропорционально действующей на тело силе,- обратно пропорционально массе тела и направлено так же, как и сила.
Особенности II закона Ньютона:
1. Верен для любых сил.
2. Сила - причина, определяет ускорение.
3. Вектор а сонаправлен с вектором F.
4. Если действуют на тело несколько сил, то берется равнодействующая.
5. Если равнодействующая равна нулю, то ускорение равно нулю. (Первый закон Ньютона)
6. Можно применять только по отношению к телам, скорость которых мала по сравнению со скоростью света.
Билет№4
План ответа
1. Импульс тела. 2. Закон сохранения импульса. 3. Применение закона сохранения импульса. 4. Реактивное движение.
Существуют величины, которые могут сохраняться при взаимодействии тел. Такими величинами являются энергия и импульс.
Импульсом тела называют векторную физическую величину, являющуюся количественной характеристикой поступательного движения тел. Импульс обозначается р. Единица измерения импульса
Р — кг • м/с. Импульс тела равен произведению массы тела на его скорость: р = mv. Направление вектора импульса р совпадает с направлением вектора скорости тела v (рис. 4).
|
|


Рис. 4
Для импульса тел выполняется закон сохранения.Имеет вид m1v1 + т2v2 = m1v1' + т2v2' где т1 и
т2 — массы тел, а v1 и v2, — скорости до взаимодействия, v1' и v2' — скорости после взаимодействия. Эта
формула и является математическим выражением закона сохранения импульса: импульс замкнутой физической системы сохраняется при любых взаимодействиях, происходящих внутри этой системы.
В механике закон сохранения импульса и законы Ньютона связаны между собой. Если на тело массой т в течение времени t действует сила и скорость его движения изменяется от v0 до v, то ускорение движения a тела равно a = (v - v0)/t. На основании второго закона Ньютона для силы F можно записать F = та = m(v - v0)/t, отсюда следует
Ft = mv - mv0.
Ft — векторная физическая величина, характеризующая действие на тело силы за некоторый промежуток времени и равная произведению силы на время t ее действия, называется импульсом силы.
Единица импульса в СИ — Н • с.
Закон сохранения импульса лежит в основе реактивного движения. Реактивное движение — это такое движение тела, которое возникает после отделения от тела его части.
Большая заслуга в развитии теории реактивного движения принадлежит К. Э. Циолковскому.
Он разработал теорию полета тела переменной массы (ракеты) в однородном поле тяготения и рассчитал запасы топлива, необходимые для преодоления силы земного притяжения; основы теории жидкостного реактивного двигателя, а так же элементы его конструкции; теорию многоступенчатых ракет, причем предложил два варианта: параллельный (несколько реактивных двигателей работают одновременно) и последовательный (реактивные двигатели работают друг за другом).В основе движения многих морских моллюсков (осьминогов, медуз, кальмаров, каракатиц) также лежит реактивный принцип.
Билет №5
Закон всемирного тяготения. Гравитационное поле. Сила тяжести. Вес тела.
Исаак Ньютон выдвинул предположение, что между любыми телами в природе существуют силы взаимного притяжения. Эти силы называют силами гравитации, или силами всемирного тяготения. Сила всемирного тяготения проявляется в Космосе, Солнечной системе и на Земле. Ньютон обобщил законы движения небесных тел и выяснил, что сила F равна:


m1 и т2 -массы взаимодействующих тел, R — расстояние между ними, G — коэффициент пропорциональности, который называется гравитационной постоянной. Численное значение гравитационной постоянной опытным путем определил Кавендиш, измеряя силу взаимодействия между свинцовыми шарами. В результате закон всемирного тяготения звучит так: между любыми материальными точками существует сила взаимного притяжения, прямо пропорциональная произведению их масс и обратно пропорциональная квадрату расстояния между ними, действующая по линии, соединяющей эти точки.
Силы всемирного тяготения действуют между любыми телами в природе, но ощутимыми они становятся при больших массах (или если хотя бы масса одного из тел велика). Закон же всемирного тяготения выполняется только для материальных точек и шаров (в этом случае за расстояние принимается расстояние между центрами шаров).
Частным видом силы всемирного тяготения является сила притяжения тел к Земле (или к другой планете). Эту силу называют силой тяжести. Под действием этой силы все тела приобретают ускорение свободного падения. В соответствии со вторым законом Ньютона g = Fтяж*m следовательно, Fтяж = mg. Сила тяжести всегда направлена к центру Земли. В зависимости от высоты h над поверхностью Земли и географической широты положения тела ускорение свободного падения приобретает различные значения. На поверхности Земли и в средних широтах ускорение свободного падения равно 9,831 м/с2.
В технике и быту широко используется понятие веса тела. Весом тела называют силу, с которой тело давит на опору или подвес в результате гравитационного притяжения к планете (рис. 1). Вес тела обозначается Р. Единица веса - Н. Так как вес равен силе, с которой тело действует на опору, то в соответствии с третьим законом Ньютона по величине вес тела равен силе реакции опоры. Поэтому, чтобы найти вес тела, необходимо определить, чему равна сила реакции опоры.

Если тело свободно падает, то в этом случае P = (g- g)m = 0. Состояние тела, в котором его вес равен нулю, называют невесомостью. Состояние невесомости наблюдается в самолете или космическом корабле при движении с ускорением свободного падения независимо от направления и значения скорости их движения. За пределами земной атмосферы при выключении реактивных двигателей на космический корабль действует только сила всемирного тяготения. Под действием этой силы космический корабль и все тела, находящиеся в нем, движутся с одинаковым ускорением, поэтому в корабле наблюдается состояние невесомости.
Билет №6
Энергия. Потенциальная и кинетическая энергия.
Движущиеся тела имеют способность выполнять работу в случае изменения скорости. Энергия, которой обладает тело вследствие своего движения, называется кинетической энергией.
Часть механической энергии, обусловленная движением тела, называется кинетической энергией - Ек.
Зависимость кинетической энергии от массы движущегося тела и его скорости
Кинетическая энергия тела, движущегося с определенной скоростью, равна работе, которую нужно выполнить, чтобы придать неподвижному телу эту скорость. Пусть до неподвижного тела массой m приложена постоянную силу F. Тогда Eк = А = Fs, где s- модуль перемещения. Подставляя в эту формулу выражения F = mа и s = v2 / 2a, получим: кинетическая энергия тела массой m, движущегося со скоростью v, выражается формулой Eк = m v2 /2.
Часть механической энергии, которая определяется взаимным расположением тел, которые взаимодействуют, называется потенциальной энергией - Еп.
Например, если сила тяжести выполняет работу во время падения груза вниз, система «поднятый груз и Земля» имеет потенциальную энергию.
Обозначим изменение потенциальной энергии  , где индексом 1 обозначены начальное состояние системы, а индексом 2 - конечный.
, где индексом 1 обозначены начальное состояние системы, а индексом 2 - конечный.
Если во время изменения взаимного расположения тел система выполняет положительную работу, ее потенциальная энергия уменьшается, а если система выполняет отрицательную работу, ее потенциальная энергия увеличивается.
Изменение потенциальной энергии ΔЕп и А работа, выполненная системой, связаны соотношением:
ΔЕп = -A.
Из этой формулы следует, что физический смысл имеет только изменение потенциальной энергии: она измеряется работой, что ее исполнила система. Выбор нулевого уровня потенциальной энергии определяется соображениями удобства для решения каждой конкретной задачи.
а) Потенциальная энергия груза, поднятого над землей. Во время поднятия груза массой m на высоту h работа выполняется mgh, поэтому потенциальная энергия системы «груз и Земля» увеличивается на mgh. Выберем как нулевой уровень потенциальной энергии состояние системы, когда груз находится на поверхности земли. Тогда Еп = mgh.
б) Потенциальная энергия деформированной пружины. Потенциальная энергия деформированной пружины равна работе, которую надо выполнить, чтобы деформировать пружину. А = kx2/2, где k - жесткость пружины, x - ее удлинение. Следовательно, потенциальная энергия деформированной пружины Eп = kx2/2.
Билет №7
План ответа
1. Определение колебательного движения. 2. Свободные колебания. 3. Превращения энергии. 4. Вынужденные колебания.
Механическими колебаниями называют движения тела, повторяющиеся точно или приблизительно через одинаковые промежутки времени. Основными характеристиками механических колебаний являются: смещение, амплитуда, частота, период. Смещение — это отклонение от положения равновесия. Амплитуда — модуль максимального отклонения от положения равновесия. Частота — число полных колебаний, совершаемых в единицу времени. Период — время одного полного колебания, т. е. минимальный промежуток времени, через который происходит повторение процесса. Период и частота связаны соотношением: v = 1/T.
Простейший вид колебательного движения — гармонические колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса (рис.).

Свободными — называют колебания, которые совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на систему, совершающую колебания. Например, колебания груза на нити (рис.).
Рассмотрим процесс превращения энергии на примере колебаний груза на нити (см. рис.).

При отклонении маятника от положения равновесия он поднимается на высоту h относительно нулевого уровня, следовательно, в точке А маятник обладает потенциальной энергией mgh. При движении к положению равновесия, к точке О, уменьшается высота до нуля, а скорость груза увеличивается, и в точке О вся потенциальная энергия mgh превратится в кинетическую энергию mv г/2. В положении равновесия кинетическая энергия имеет максимальное значение, а потенциальная энергия минимальна. После прохождения положения равновесия происходит превращение кинетической энергии в потенциальную, скорость маятника уменьшается и при максимальном отклонении от положения равновесия становится равной нулю. При колебательном движении всегда происходят периодические превращения его кинетической и потенциальной энергий.
При свободных механических колебаниях неизбежно происходит потеря энергии на преодоление сил сопротивления. Если колебания происходят под действием периодически действующей внешней силы, то такие колебания называют вынужденными.
При совпадении частоты внешней силы и частоты собственных колебаний тела амплитуда вынужденных колебаний резко возрастает. Такое явление называют механическим резонансом.
 Хт— амплитуда
Хт— амплитуда
w — частота внешней силы
w0 — частота собственных колебаний
Рис. 1
Явление резонанса может быть причиной разрушения машин, зданий, мостов, если собственные их частоты совпадают с частотой периодически действующей силы. Поэтому, например, двигатели в автомобилях устанавливают на специальных амортизаторах, а воинским подразделениям при движении по мосту запрещается идти «в ногу».
Билет №8
План ответа
1. Основные положения. 2. Опытные доказательства. 3. Микро-характеристики вещества.
Молекулярно-кинетическая теория — это раздел физики, изучающий свойства различных состояний вещества, основывающийся на представлениях о существовании молекул и атомов, как мельчайших частиц вещества. В основе МКТ лежат три основных положения:
1. Все вещества состоят из мельчайших частиц: молекул, атомов или ионов.
2. Эти частицы находятся в непрерывном хаотическом движении, скорость которого определяет температуру вещества.
3. Между частицами существуют силы притяжения и отталкивания, характер которых зависит от расстояния между ними.
Основные положения МКТ подтверждаются многими опытными фактами. Существование молекул, атомов и ионов доказано экспериментально, молекулы достаточно изучены и даже сфотографированы с помощью электронных микроскопов. Способность газов неограниченно расширяться и занимать весь предоставленный им объем объясняется непрерывным хаотическим движением молекул. Упругость газов, твердых и жидких тел, способность жидкостейсмачивать некоторые твердые тела, процессы окрашивания, склеивания, сохранения формы твердыми телами и многое другое говорят о существовании сил притяжения и отталкивания между молекулами. Явление диффузии — способность молекул одного вещества проникать в промежутки между молекулами другого — тоже подтверждает основные положения МКТ. Явлением диффузии объясняется, например, распространение запахов, смешивание разнородных жидкостей, процесс растворения твердых тел в жидкостях, сварка металлов путем их расплавления или путем давления. Подтверждением непрерывного хаотического движения молекул является также и броуновское движение — непрерывное хаотическое движение микроскопических частиц, нерастворимых в жидкости.
Движение броуновских частиц объясняется хаотическим движением частиц жидкости, которые сталкиваются с микроскопическими частицами и приводят их в движение. Опытным путем было доказано, что скорость броуновских частиц зависит от температуры жидкости. Теорию броуновского движения разработал А. Эйнштейн. Законы движения частиц носят статистический, вероятностный характер. Известен только один способ уменьшения интенсивности броуновского движения — уменьшение температуры. Существование броуновского движения убедительно подтверждает движение молекул.
Любое вещество состоит из частиц, поэтому количество вещества принято считать пропорциональным числу частиц, т. е. структурных элементов, содержащихся в теле, v.
Единицей количества вещества является моль. Моль — это количество вещества, содержащее столько же структурных элементов любого вещества, сколько содержится атомов в 12 г углерода С12. Отношение числа молекул вещества к количеству вещества называют постоянной Авогадро:
na= N/v. na = 6,02 • 1023моль-1.
Постоянная Авогадро показывает, сколько атомов и молекул содержится в одном моле вещества. Молярной массой называют величину, равную отношению массы вещества к количеству вещества:
М = m/v.
Молярная масса выражается в кг/моль. Зная молярную массу, можно вычислить массу одной молекулы:
m0 = m/N = m/vNA = М/NA
Средняя масса молекул обычно определяется химическими методами, постоянная Авогадро с высокой точностью определена несколькими физическими методами. Массы молекул и атомов со значительной степенью точности определяются с помощью масс-спектрографа.
Массы молекул очень малы. Например, масса молекулы воды: т = 29,9 •10 -27 кг.
Молярная масса связана с относительной молекулярной массой Mr. Относительная молярная масса — это величина, равная отношению массы молекулы данного вещества к 1/12 массы атома углерода С12. Если известна химическая формула вещества, то с помощью таблицы Менделеева может быть определена его относительная масса, которая, будучи выражена в килограммах, показывает величину молярной массы этого вещества.
Диаметром молекулы принято считать минимальное расстояние, на которое им позволяют сблизиться силы отталкивания. Однако понятие размера молекулы является условным. Средний размер молекул порядка 10-10 м.
Билет №9
План ответа
1. Понятие идеального газа, свойства. 2. Объяснение давления газа. 3. Необходимость измерения температуры. 4. Физический смысл температуры. 5. Температурные шкалы. 6. Абсолютная температура.
Для объяснения свойств вещества в газообразном состоянии используется модель идеального газа. Идеальным принято считать газ, если:
а) между молекулами отсутствуют силы притяжения, т. е. молекулы ведут себя как абсолютно упругие тела;
б) газ очень разряжен, т. е. расстояние между молекулами намного больше размеров самих молекул;
в) тепловое равновесие по всему объему достигается мгновенно. Условия, необходимые для того, чтобы реальный газ обрел свойства идеального, осуществляются при соответствующем разряжении реального газа. Некоторые газы даже при комнатной температуре и атмосферном давлении слабо отличаются от идеальных.
Основными параметрами идеального газа являются давление, объем и температура.
Одним из первых и важных успехов МКТ было качественное и количественное объяснение давления газа на стенки сосуда. Качественное объяснение заключается в том, что молекулы газа при столкновениях со стенками сосуда взаимодействуют с ними по законам механики как упругие тела и передают свои импульсы стенкам сосуда.
На основании использования основных положений молекулярно-кинетической теории было получено основное уравнение МКТ идеального газа, которое выглядит так: р = 1/3 т0пv2.
Здесь р — давление идеального газа, m0 —
масса молекулы, п — концентрация молекул, v 2 — средний квадрат скорости молекул.
Обозначив среднее значение кинетической энергии поступательного движения молекул идеального газа Еk получим основное уравнение МКТ идеального газа в виде: р = 2/3nЕk.
Однако, измерив только давление газа, невозможно узнать ни среднее значение кинетической энергии молекул в отдельности, ни их концентрацию. Следовательно, для нахождения микроскопических параметров газа нужно измерение какой-то еще физической величины, связанной со средней кинетической энергией молекул. Такой величиной в физике является температура. Температура — скалярная физическая величина, описывающая состояние термодинамического равновесия (состояния, при котором не происходит изменения микроскопических параметров). Как термодинамическая величина температура характеризует тепловое состояние системы и измеряется степенью его отклонения от принятого за нулевое, как молекулярно-кинетическая величина характеризует интенсивность хаотического движения молекул и измеряется их средней кинетической энергией.
Ek = 3/2 kT, где k = 1,38 • 10-23 Дж/К и называется постоянной Больцмана.
Температура всех частей изолированной системы, находящейся в равновесии, одинакова. Измеряется температура термометрами в градусах различных температурных шкал. Существует абсолютная термодинамическая шкала (шкала Кельвина) и различные эмпирические шкалы, которые отличаются начальными точками. До введения абсолютной шкалы температур в практике широкое распространение получила шкала Цельсия (за О °С принята точка замерзания воды, за 100 °С принята точка кипения воды при нормальном атмосферном давлении).
Единица температуры по абсолютной шкале называется Кельвином и выбрана равной одному градусу по шкале Цельсия 1 К = 1 °С. В шкале Кельвина за ноль принят абсолютный ноль температур, т. е. температура, при которой давление идеального газа при постоянном объеме равно нулю. Вычисления дают результат, что абсолютный ноль температуры равен -273 °С. Таким образом, между абсолютной шкалой температур и шкалой Цельсия существует связь Т = t °С + 273. Абсолютный ноль температур недостижим, так как любое охлаждение основано на испарении молекул с поверхности, а при приближении к абсолютному нулю скорость поступательного движения молекул настолько замедляется, что испарение практически прекращается. Теоретически при абсолютном нуле скорость поступательного движения молекул равна нулю, т. е. прекращается тепловое движение молекул.
Билет №10
Работа силы. Мощность.
Работа силы равна произведению модулей силы и перемещения и косинуса угла между ними. Эта формула справедлива в том случае, когда сила постоянна и перемещение тела происходит вдоль прямой.
A= F|∆r|cosα
Знак работы определяется знаком косинуса угла между силой и перемещением.
Если α<90˚, то A>0,
Если α>90˚, то A<0
Если α=0, то A=0
Если на тело действует несколько сил, то полная работа (сумма работ всех сил) равна работе результирующей силы.
A = F1r | ∆r|+F2r |∆r| +…=A1+A2+….
В Международной системе единиц работа измеряется в джоулях (Дж)
1 Дж = 1 Н·1 м = 1 Н·м
Джоуль – это работа, совершаемая силой 1 Н на перемещение 1 м, если направления силы и перемещения совпадают.
Мощностью называют отношение работы А к интервалу времени ∆t, за который эта работа совершена. N = A/∆t
Если мы в формулу мощности подставим формулу работы, то получится, что мощность равна произведению модуля вектора силы на модуль вектора скорости и на косинус угла между
|
|
|

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!