Это, собственно, то, с чего начинался Юникод: для кодирования одного символа используются двухбайтовые целые. Этого хватает для того, чтобы хранить большинство нужных и распространенных на практике символов. И только для редких символов, включенных в Юникод позднее, используются пары двухбайтовых целых.
Кстати, UCS-2 — это как раз UTF-16 без этих дополнительных символов, то есть, строго, символ кодируется двумя байтами.
На практике редкие символы действительно редки (часто встречались с древнегреческой музыкальной грамотой?), поэтому во многих системах для внутреннего представления символов используется именно UTF-16, например в NTFS для имен файлов, в Delphi для WideString'ов, и Java, насколько мне известно, тоже внутри вся в UTF-16 работает со строками.
Однако двухбайтовость делает затруднительным использование UTF-16 для обмена данными из-за двух проблем: наличия нулевых байтов в строке и разночтения порядка следования старшего и младшего байтов на разных платформах.
UTF-32 (или, что почти одно и то же — UCS-4)
Это — форма для перфекционистов. Для представления символа используется строго 4 байта, которыми можно представить абсолютно любой юникодный символ. С недавнего времени тот же Python на большинстве платформ использует именно четырехбайтовое представление для юникодных строк.
Отличия от UCS-4 совсем умозрительные и непрактические.
Минус у этого представления, помимо плохой переносимости, как у UTF-16, еще и в том, что UTF-32 попросту занимает еще больше места.
Коды в стандарте Юникод разделены на несколько областей. Область с кодами от U+0000 до U+007F содержит символы набора ASCII с соответствующими кодами. Далее расположены области знаков различных письменностей, знаки пунктуации и технические символы. Часть кодов зарезервирована для использования в будущем. Под символы кириллицы выделены области знаков с кодами от U+0400 до U+052F, от U+2DE0 до U+2DFF, от U+A640 до U+A69F.
BOM
Byte Order Mark (BOM)(метка порядка байтов) - Unicode символ, используемый для индикации порядка байтов текстового файла. Его кодовый символ U+FEFF (ZERO WIDTH NON-BREAKING SPACE) неразрывный пробел с нулевой шириной, также именуемый меткой порядка байтов (англ. byte order mark, BOM). По спецификации его использование не является обязательным, однако если BOM используется, то он должен быть установлен в начале текстового файла. Помимо своего конкретного использования в качестве указателя порядка байтов, символ может также указать, какой кодировкой Unicode закодирован текст.
По наличию сигнатуры программы могут автоматически определить, является ли файл закодированным в UTF-8, однако файлы с такой сигнатурой могут некорректно обрабатываться старыми программами, в частности xml-анализаторами. Такие редакторы, как Notepad++, Notepad2 и Kate, позволяют явно указывать, следует ли добавлять сигнатуру при сохранении UTF-файлов.
Кодирование целых чисел
Прямойкод
При записи числа в прямом коде (sign-and-magnitude method) старший разряд (most significant bit) является знаковым разрядом (sign bit). Если его значение равно нулю, то число положительное, если единице — отрицательное. В остальных разрядах (которые называются цифровыми) записывается двоичное представление модуля числа. Например, число −5 в восьмибитовом типе данных, использующем прямой код, будет выглядеть так: 10000101.
| Рис. 1. Нумерация двоичных чисел в прямом представлении
|

Таким способом в

-битовом типе данных можно представить диапазон чисел
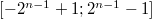
.
Достоинства метода:
получить прямой код числа достаточно просто.
Недостатки:
выполнение арифметических операций с отрицательными числами требует усложнения архитектуры центрального процессора (например, для вычитания невозможно использовать сумматор, необходима отдельная схема для этого);
существуют два нуля ("+0" и "−0"), из-за чего усложняется арифметическое сравнение.
Из-за этого прямой код используется очень редко.
Код со сдвигом
 При использовании кода со сдвигом (excess-
При использовании кода со сдвигом (excess- 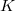 , где
, где  ; также говорят biased representation) целочисленный отрезок от нуля до
; также говорят biased representation) целочисленный отрезок от нуля до  (
( — количество бит) сдвигается влево на
— количество бит) сдвигается влево на 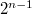 , а затем получившиеся на этом отрезке числа последовательно кодируются в порядке возрастания кодами от 000...0 до 111...1. Например, число −5 в восьмибитовом типе данных, использующем код со сдвигом, превратится в −5 + 128 = 123, то есть будет выглядеть так: 01111011.
, а затем получившиеся на этом отрезке числа последовательно кодируются в порядке возрастания кодами от 000...0 до 111...1. Например, число −5 в восьмибитовом типе данных, использующем код со сдвигом, превратится в −5 + 128 = 123, то есть будет выглядеть так: 01111011.
По сути, при таком кодировании:
к кодируемому числу прибавляют 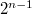 ;
;
переводят получившееся число в двоичную систему исчисления.
Можно получить диапазон значений  .
.
Достоинства метода:
не требуется усложнение архитектуры процессора;
нет проблемы двух нулей.
Недостатки:
при арифметических операциях нужно учитывать смещение, то есть проделывать на одно действие больше (например, после «обычного» сложения двух чисел у результата будет двойное смещение, одно из которых необходимо вычесть);
ряд положительных и отрицательных чисел несимметричен.
Из-за необходимости усложнять арифметические операции код со сдвигом для представления целых чисел используется не часто, но зато применяется для хранения порядка вещественного числа.
Дополнительный код (дополнение до единицы )
В качестве альтернативы представления целых чисел может использоваться код с дополнением до единицы (англ. Ones' complement).
Алгоритм получения кода числа:
если число положительное, то в старший разряд (который является знаковым) записывается ноль, а далее записывается само число;
| Рис. 3. Нумерация двоичных чисел в представлении c дополнением до единицы. В отличие от кода со сдвигом, нулю соответствуют коды 00...000 и 11...111
|
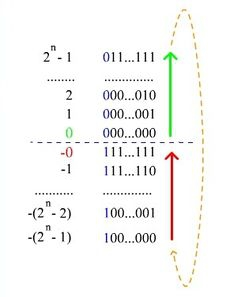
если число отрицательное, то код получается инвертированием представления модуля числа (получается
обратный код)
Пример: переведём число −13 в восьмибитовый код. Прямой код модуля −13 --- 00001101, инвертируем и получаем 11110010. Для получения из дополнительного кода самого числа достаточно инвертировать все разряды кода.
Таким способом можно получить диапазон значений 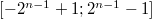 .
.
Достоинства метода:
Простое получение кода отрицательных чисел
Недостатки метода:
выполнение арифметических операций с отрицательными числами требует усложнения архитектуры центрального процессора
существуют два нуля ("+0" и "−0")



 Таким способом в
Таким способом в  -битовом типе данных можно представить диапазон чисел
-битовом типе данных можно представить диапазон чисел 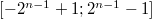 .
.
 При использовании кода со сдвигом (excess-
При использовании кода со сдвигом (excess- 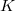 , где
, где  ; также говорят biased representation) целочисленный отрезок от нуля до
; также говорят biased representation) целочисленный отрезок от нуля до  (
(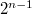 , а затем получившиеся на этом отрезке числа последовательно кодируются в порядке возрастания кодами от 000...0 до 111...1. Например, число −5 в восьмибитовом типе данных, использующем код со сдвигом, превратится в −5 + 128 = 123, то есть будет выглядеть так: 01111011.
, а затем получившиеся на этом отрезке числа последовательно кодируются в порядке возрастания кодами от 000...0 до 111...1. Например, число −5 в восьмибитовом типе данных, использующем код со сдвигом, превратится в −5 + 128 = 123, то есть будет выглядеть так: 01111011. .
. если число отрицательное, то код получается инвертированием представления модуля числа (получается обратный код)
если число отрицательное, то код получается инвертированием представления модуля числа (получается обратный код)


