Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...
Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...
Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации...
Интересное:
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Дисциплины:
 2017-06-29 |
 348 |
из
5.00
|
Заказать работу |
|
|
|
|
Для того чтобы функция f, x 
X, имела в (конечной или бесконечно удаленной) точке x0 конечный предел, необходимо и достаточно, чтобы для любого 
> 0 существовала такая окрестность U(x0) точки x0, что для любых x' X 
U(x0) и x" X U(x0) выполнялось бы неравенство | f (x") - f (x')| < .
Предел ф-ции по направлению
Рассмотрим некоторую функцию 
, заданную во всех точках окрестности точки 
, кроме, быть может, точки ; пусть 
- произвольный вектор длины единица 
и 
- скаляр. Точки вида 
образуют выходящий из луч в направлении вектора 
. Для каждого можно рассматривать функцию
от скалярной переменной 
, где 
есть число, зависящее от . Предел этой функции (от одной переменной )
,
если он существует, естественно назвать пределом в точке по направлению вектора .
Непрерывность
Функция 
непрерывна в точке 
, если она опред. в некот. окр. точки Mo и 
Вопрос 15 Частные производные. Дифференцируемость ф-ций неск. переменных, осн. теоремы, необ. и достат. условие дифф-ти, дифф-ие сложной ф-ции, инвариантность формы 1-ого дифф-ла.
Функция называется дифференцируемой в данной точке, если ее полное приращение в этой точке может быть представлено в виде: 
, где А1, А2, …, Аm – некоторые не зависящие от ∆х1, ∆х2, …, ∆хm числа, а α1, α2, …, αm – бесконечно малые при 
функции, равные 0 при ∆х1=∆х2=…∆хm=0.
Частная производная функции z=f(x,y) по х – предел отношения частного приращения функции по х к приращению Δх при Δх→0, если он существует и конечен:
Частная производная функции z=f(x,y) по y- – предел отношения частного приращения функции по y к приращению Δy при Δy→0, если он существует и конечен:
Полный дифференциал функции z=f(x,y) - главная линейная относительно 
и ∆у часть приращения функции ∆z в точке (х,у): dz= fx(x,y)dx+ fy (x,y)dy
|
|
Если функция f(x,y) определена в некоторой области D, то её частные производные f ’x(x,y), f ’y(x,y), тоже будут определены в той же области или её части. Будем называть эти производные производными I-ого порядка. Производные этих функций производными II-ого порядка.
Необх. и дост. условие дифференцируемости
Напомним, что функция одной переменной 
называется дифференцируемой в точке 
, если приращение функции представимо в виде
,
где 
― некоторое действительное число, зависящее от , а 
-бесконечно малая функция более высокого порядка малости, чем 
, при 
.
Необходимым и достаточным условием дифференцируемости функции 
в точке является существование производной
.
Выясним, как переносятся условия дифференцируемости на случай функции двух переменных.
Определение. Функция 
называется дифференцируемой в точке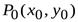 
, если ее полное приращение в этой точке можно представить в виде
,(1)
Дифференцирование сложной ф-ции
Пусть задана функция двух переменных 
и пусть переменные 
и 
сами являются непрерывными функциями независимых переменных 
и 
: 
, 
. (*)
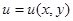Таким образом,
,
т.е. 
является сложной функцией переменных и . Выясним, как найти ее частные производные по аргументам и , не делая непосредственной подстановки. При этом будем предполагать, что все рассматриваемые функции имеют непрерывные частные производные по всем своим аргументам.
Сначала найдем производную 
. Для этого дадим аргументу приращение 
, сохраняя значение неизменным. Тогда в силу уравнений (*) получат приращения 
и 
.
Но если и получают приращения и , то функция получит приращение 
, определяемое формулой:
.
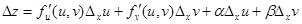Разделим обе части последнего равенства на :
.
Если 
, то 
и 
(в силу непрерывности функций и ). Но тогда 
и 
тоже стремятся к нулю. Переходя к пределу при , получим
, 
, 
,
и, следовательно,
. (1)
Аналогично находим производную по переменной :
. (2)
Вывод. Частная производная сложной функции равна сумме произведений частных производных заданной функции по промежуточным аргументам ( и ) на частные производные этих аргументов ( и ) по соответствующей независимой переменной ( и ), где 
и 
— некоторые постоянные, зависящие от и 
; 
и 
— функции от и 
, стремящиеся к нулю при и 
, то есть 
, 
.
|
|
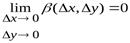Равенство (1) выражает условие дифференцируемости функции в точке .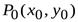
Определение. Функцию , дифференцируемую в каждой точке некоторого множества, называют дифференцируемой на этом множестве.
Инвариантность формы 1-ого диф-ла
Если xi(t) непрерывно диф-ма на t= t0(t01+ t02 +…+ t0m), а y=f(x); x=(x1,x2,…xn) непрерыв.. диф-ма в т. x0=(x01,x02,…x0n), xoi (to), то ф-ция y=f(x(t)) диф-ма в точке tо и справедливо равенство 
|
|
|
Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...
Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...
История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...
Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!