Логические элементы могут использоваться как самостоятельные части схемы, так и входить в состав более сложной цифровой комбинационной схемы или схемы с памятью. Как самостоятельные части схемы, логические элементы могут применяться в качестве управляющей логики какого-либо устройства, а также в качестве генератора прямоугольных импульсов с подключённой ёмкостью или кварцевым резонатором. В качестве комбинационных схем логические элементы используются в составе микросхем БИС и СБИС, а также в дешифраторах и шифраторах, выполненных в виде отдельных микросхем. Также, логические элементы могут входить в состав схем с памятью (триггеры, регистры, счётчики и т.д.), выполненных в виде отдельной микросхемы или в составе других микросхем.
Поскольку любая логическая операция может быть представлена в виде комбинации трех основных, любые устройства компьютера, производящие обработку или хранение информации, могут быть собраны из базовых логических элементов, как из “кирпичиков”.
Преобразование сигнала логическим элементом задается таблицей состояний, которая фактически является таблицей истинности, соответствующей логической функции, только представлена в форме логических схем. В такой форме удобно изображать цепочки логических операций и производить их вычисления.
Алгоритм построения логических схем.
1. Определить число логических переменных.
2. Определить количество логических операций и их порядок.
3. Изобразить для каждой логической операции соответствующий ей логический элемент.
4. Соединить логические элементы в порядке выполнения логических операций.
Пример. По заданной логической функции 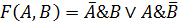 построить логическую схему.
построить логическую схему.
Решение.
1. Число логических переменных = 2 (A и B).
2. Количество операций = 5 (2 инверсии, 2 конъюнкции, 1 дизъюнкция). Сначала выполняются операции инверсии, затем конъюнкции, в последнюю очередь операция дизъюнкции.
3. Схема будет содержать 2 инвертора, 2 конъюнктора и 1 дизъюнктор.
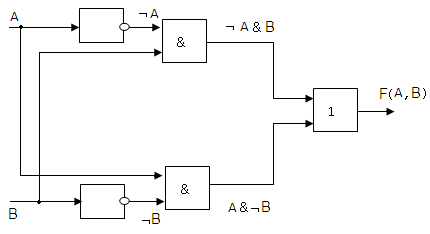
4. Построение надо начинать с логической операции, которая должна выполняться последней. В данном случае такой операцией является логическое сложение, следовательно, на выходе должен быть дизъюнктор. На него сигналы подаются с двух конъюнкторов, на которые, в свою очередь, подаются один входной сигнал нормальный и один инвертированный (с инверторов).
Задания
В данной работе необходимо составить таблицу истинности логического выражения, построить схему логической функции и упростить логическое выражение заданные каждому студенту в соответствии с его вариантом, записать ход рассуждений и полученные результаты.
| Вариант
| Логическая функция
|
|
|
|
|
| f (x, y,z) = c × b + c × a
|
|
| f (x, y,z) = a × b + c × a
|
|
| f (x, y,z) = a × b + c × a × b
|
|
| f (x, y,z) = a × b × c + c × b
|
|
| f (x, y,z) = a × b × c + c × a
|
|
| f (x, y,z) = a × b × c + c × a
|
|
| f (x, y,z) = a × b × c + c × a
|
|
| f (x, y,z) = a × b × c + c × a
|
|
| f (x, y,z) = a × b × c + c × a
|
|
| f (x, y,z) = a × b × c + c × a
|
|
| f (x, y,z) = a × b × c + c × a
|
|
| f (x, y,z) = a × b × c + c × a
|
|
| f (x, y,z) = a × b × c + c × a
|
|
| f (x, y,z) = a × b × c + c × b × a
|
|
| f (x, y,z) = a × b × c + c × a
|
|
| f (x, y,z) = a × b × c + c × a
|
|
| f (x, y,z) = a × b × c + c × a
|
|
| f (x, y,z) = a × b × c + c × a
|
|
| f (x, y,z) = a × b × +c × b × a
|
|
| f (x, y,z) = a × b × +c × b × a
|
|
| f (x, y,z) = a × b × +c × b × a
|
|
| f (x, y,z) = a × b + c × b × a
|
|
| f (x, y,z) = b × c + c × b × a
|
|
| f (x, y,z) = b × c + c × a
|
Вопросы для защиты работы
1. Что такое высказывание (приведите пример)?
2. Что такое составное высказывание (приведите пример)?
3. Как называются и как обозначаются (в языке математики) следующие операции: ИЛИ, НЕ, И, ЕСЛИ … ТО, ТОГДА И ТОЛЬКО ТОГДА, ЛИБО …ЛИБО?
4. Укажите приоритеты выполнения логических операций.
5. Составьте таблицу истинности для следующих операций: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция.
6. По заданной логической функции построить логическую схему (индивидуальное задание).
7. Какие логические выражения называются равносильными?
8. Записать основные законы алгебры логики.
Лабораторная работа № 3





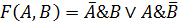 построить логическую схему.
построить логическую схему.



