Если доказуема формула, то она общезначима.
Аксиоматическая система является непротиворечивой, если из нее невозможно вывести формулу и ее отрицания.
Полнота формальной системы: Если 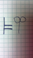 , то
, то 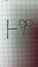 . Всякая общезначимая формула должна быть доказуема, и всякая доказуемая формула есть общезначимая. то эта теорема (Т) является неполной.
. Всякая общезначимая формула должна быть доказуема, и всякая доказуемая формула есть общезначимая. то эта теорема (Т) является неполной.
Формула называется разрешимой, если у нас имеется общий метод проверки общезначимости(доказуемости) формулы.
Логика высказываний разрешима, т.к. посредствам таблиц истинности мы можем всегда проверить является ли формула общезначимой. Но тогда по теореме: если 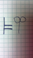 , то
, то 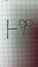 , что формула разрешима относительно свойства доказуемости.
, что формула разрешима относительно свойства доказуемости.
Но некоторые (неклассические) логики являются неразрешимыми. Но неразрешима и логика первого порядка, следовательно, не существует общего метода проверки общезначимости формул.
Для одноместных предикатов методы существуют, но для двухместных и трехместных предикатов общих методов не существует. А есть лишь локальные методы, некоторые покоятся на рассуждении от противного.
Логические отношения между простыми категорическими суждениями. Непосредственные вывода по логическому квадрату
Простое категорическое суждение- простое суждение, в котором что-то утверждается и отрицается относительно предмета мысли, а между субъектом и предикатом устанавливается категорическая (утвердительная, отрицательная) связь: отношение тождества, подчинения, частичного совпадения, противоречия, противоположности, соподчинения
Структура простого категорического суждения: состоит из субъекта, предиката, связки.
Классификация
I. По качественному признаку (характеру связки), простые категорические суждения делятся на утвердительные и отрицательные.
В утвердительных суждениях говорится о наличии свойства у предмета и принадлежности предмета субъекту: S есть Р.
Отрицательные суждения говорят об отсутствии свойств у предмета: S не есть Р, или S есть не Р.
II. По количественному (объемному) показателю, выражаемому квантором, простые категорические суждения делятся на единичные, частные и общие.
Единичное суждение:субъект суждения - единичное понятие (название города).
Частное суждение - совокупность предметов, но не вся, подчеркивается квантором: «Некоторые S есть Р». В количественном отношении частные суждения неопределенны.
Общее суждение о всей предметной области, на которую направлено внимание. Суждение с квантором (все, ни один, каждый, без исключения) перед субъектом: «Все S есть Р».
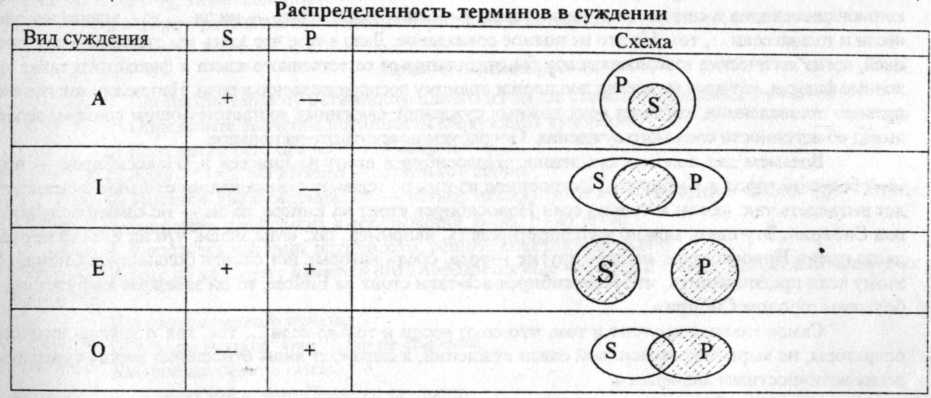
СООТНОШЕНИЕ ОБЪЕМОВ ТЕРМИНОВ: исходя из количественной классификации можно определить распределенность терминов в суждении (чтобы понимать смысл суждений, строить умозаключения, надо знать, как относятся субъект и предикат суждения. Для выражения отношений субъекта и предиката используют операцию распределения терминов в суждении)
Формальнологический анализ этих суждений выявляет структурные закономерности их, не зависящие от содержания. Исходя из структуры общих (утвердительного и отрицательного) суждений можно, не зная содержания, сказать, что их субъекты взяты в полном объеме (для отрицательного - в полном объеме исключаются из рассмотрения). КОРОЧЕ: благодаря этому нам пофигу на смысл высказывания. В дальнейшем, не затрачивая кучу времени на размышления, люди делают выводы просто подставляя термины в эти схемы-кружочки,проводя с ними не хитрые махинации.Будучи философом я могу проверить вывод химика, не понимая о чем идет речь вовсе.





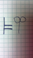 , то
, то 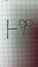 . Всякая общезначимая формула должна быть доказуема, и всякая доказуемая формула есть общезначимая. то эта теорема (Т) является неполной.
. Всякая общезначимая формула должна быть доказуема, и всякая доказуемая формула есть общезначимая. то эта теорема (Т) является неполной.




