Рассмотрим математическую сущность устойчивости и неустойчивости линейных стационарных САУ. Согласно данному выше физическому определению устойчивость зависит только от характера свободного движения системы. Свободное движение линейной или линеаризованной системы описывается однородным дифференциальным уравнением
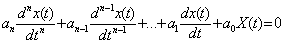 ,
,
где x(t) = xсв(t) - свободная составляющая выходной величины системы.
Вынужденная составляющая выходной величины, зависящая от вида внешнего воздействия и правой части дифференциального уравнения (2.1), на устойчивость системы не влияет.
Система является устойчивой, если свободная составляющая xсв(t) переходного процесса с течением времени стремится к нулю, т.е. если
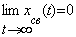
Очевидно, что при этом выходная величина системы будет стремиться к вынужденной составляющей, определяемой правой частью уравнения. Устойчивость в смысле условия (4.2) принято называть асимптотической.
Если свободная составляющая неограниченно взрастает, т.е. если
 ,
,
то система неустойчива.
Наконец, если свободная составляющая не стремится ни к нулю, ни к бесконечности, то система находится на границе устойчивости.
Найдем общее условие, при котором система, описываемая уравнением, устойчива. Решение уравнения
xсв(t) =  ,
,
где Ck - постоянные интегрирования, зависящие от начальных условий;
pk - корни характеристического уравнения
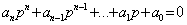 .
.
Корни характеристического уравнения могут быть действительными (pk=ak), мнимыми (pk=jbk) и комплексными
pk=ak ± jbk,
причем как комплексные, так и мнимые корни попарно сопряжены.
Свободная составляющая (4.4) удовлетворяет условию устойчивости, если каждое слагаемое вида 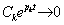 . Характер этой функции времени зависит от вида корня pk.
. Характер этой функции времени зависит от вида корня pk.
Рассмотрим все возможные случаи расположения корней характеристического уравнения на комплексной плоскости и соответствующие им функции xсв(t), которые показаны внутри кругов (как на экране осциллографа)
1) Каждому действительному корню pk=ak в решении соответствует слагаемое вида
xсвk(t) = 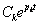 .
.
Если ak<0 (корень p1), то функция плавно стремится к нулю. Если ak>0 (корень p3), то функция неограниченно возрастает. Если ak=0 (корень p2), то эта функция остается постоянной.
2) Каждой паре сопряженных комплексных корней pk=ak+jbk и pk+1=ak‑jbk в решении соответствуют два слагаемых, которые могут быть объединены в одно слагаемое
xсвk(t) = 2 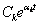 sin(bkt+yk).
sin(bkt+yk).
Функция представляет собой синусоиду с частотой bk и амплитудой, изменяющейся по экспоненте. Если ak < 0 то колебательная составляющая будет затухать.
Если ak > 0 (корни p8 и p9),то амплитуда колебаний будет неограниченно возрастать. Наконец, если ak = 0 (корни p6 и p7), т.е. оба сопряженных корня - мнимые (pk=jbk, pk+1=-jbk), то xсвk(t)=2 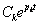 sin(bkt+yk) - незатухающая синусоида bk.
sin(bkt+yk) - незатухающая синусоида bk.
Если среди корней характеристического уравнения (4.5) имеются l равных между собой корней pl, то в решении (4.4) вместо l слагаемых вида 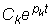 появится одна составляющая
появится одна составляющая
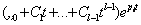 .
.
Учитывая, что функция вида 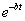 при любом b убывает быстрее, чем возрастают слагаемые вида
при любом b убывает быстрее, чем возрастают слагаемые вида 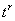 , можно доказать, что и в случае кратности корней решение будет стремиться к нулю лишь при отрицательности действительной части кратных корней pl.
, можно доказать, что и в случае кратности корней решение будет стремиться к нулю лишь при отрицательности действительной части кратных корней pl.





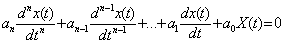 ,
,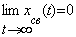
 ,
, ,
,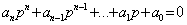 .
.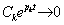 . Характер этой функции времени зависит от вида корня pk.
. Характер этой функции времени зависит от вида корня pk.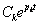 .
.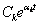 sin(bkt+yk).
sin(bkt+yk).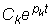 появится одна составляющая
появится одна составляющая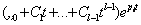 .
.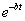 при любом b убывает быстрее, чем возрастают слагаемые вида
при любом b убывает быстрее, чем возрастают слагаемые вида 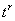 , можно доказать, что и в случае кратности корней решение будет стремиться к нулю лишь при отрицательности действительной части кратных корней pl.
, можно доказать, что и в случае кратности корней решение будет стремиться к нулю лишь при отрицательности действительной части кратных корней pl.


