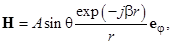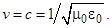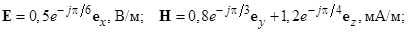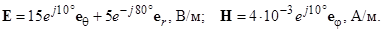Грачев С. В.
ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ И ВОЛНЫ
Методические указания для практических занятий
Санкт-Петербург
СОДЕРЖАНИЕ
1. Элементы векторного анализа...................................................................................................... 3
Теоретические сведения.................................................................................................... 3
1.1. Скалярные и векторные и поля........................................................................................ 4
2. Электростатика и магнитостатика............................................................................................... 7
Теоретические сведения.................................................................................................... 7
2.1 Электростатические поля.................................................................................................. 8
2.2. Стационарные магнитные поля....................................................................................... 9
3. Основные положения электродинамики................................................................................... 10
Теоретические сведения.................................................................................................. 10
3.1. Уравнения Максвелла..................................................................................................... 12
3.2. Энергетические соотношения в электродинамике...................................................... 14
3.3. Граничные условия для векторов электромагнитного поля....................................... 15
4. Плоские электромагнитные волны............................................................................................ 17
Теоретические сведения.................................................................................................. 17
4.1. Основные характеристики плоских волн..................................................................... 18
4.2. Электромагнитные волны в средах с частотной дисперсией..................................... 21
5. Отражение и преломление плоских электромагнитных волн................................................ 23
Теоретические сведения.................................................................................................. 23
5.1. Падение плоской волны на границу раздела двух диэлектрических сред............... 27
5.2. Падение плоской волны на границу раздела с реальным металлом.......................... 33
5.3. Падение плоской волны на идеально проводящую плоскость.................................. 36
Методические указания предназначены для проведения практических занятий по курсу «Электромагнитные поля и волны» для бакалавров ФРТ. Методические указания содержат краткие теоретические сведения и задачи по разделам, изучаемым в лекционном курсе. Задачи повышенной сложности обозначены звездочкой.
ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА
Теоретические сведения
Градиент, дивергенция и ротор в обобщенной криволинейной ортогональной правовинтовой системе координат:

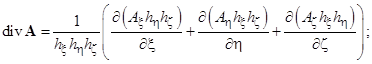
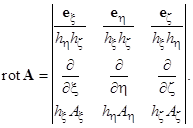
Градиент, дивергенция, ротор, оператор набла и оператор Лапласа в декартовой системе координат:
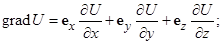

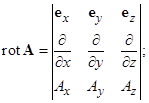


Полезные соотношения векторного анализа:
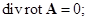

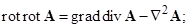
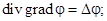

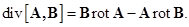
1.1. Скалярные и векторные и поля
1.1.1. В декартовой системе координат задано векторное поле А. Постройте качественно картину силовых линий данного поля. Рассмотрите прямоугольный контур L, расположенный в плоскости z = 0 и образованный отрезками прямых, соединяющих точки с координатами (0,0), (а,0), (а,b) и (0,b). Определите: а) циркуляцию вектора А по контуру L с направлением обхода по часовой стрелке, если смотреть с конца орта e z; б) поток вектора А через поверхность S, ограниченную контуром L и имеющую единичный вектор нормали e z. Решите задачу для следующих вариантов:
1) 
2) 
3) 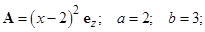
4) 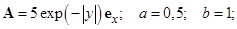
5) 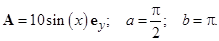
1.1.2. В цилиндрической системе координат задано векторное поле А. Постройте качественно картину силовых линий данного поля. Рассмотрите контур L, расположенный в плоскости z = 0 и образованный полуокружностями с радиусами а и b (b > а), лежащими в полуплоскости у > 0, и двумя отрезками прямых, соединяющими полуокружности в точках оси x с координатами х 1 = –b, х 2= –а и х 3 = а, х 4 = b. Определите: а) циркуляцию поля А по контуру L с направлением обхода по часовой стрелке, если смотреть с конца орта e z; б) поток поля А через поверхность S, ограниченную контуром L и имеющую единичный вектор нормали e z. Решите задачу для следующих вариантов:
1) 
2) 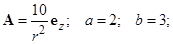
3) 
4) 
5) 
1.1.3. Вычислите 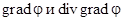 для следующих вариантов:
для следующих вариантов:
1) 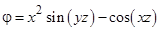 ; 2)
; 2) 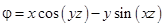 ;
;
3) 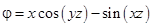 ; 4)
; 4)  ;
;
5) 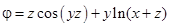 ; 6)
; 6) 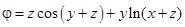 ;
;
7) 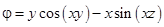 ; 8)
; 8) 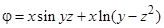 ;
;
9) 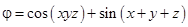 ; 10)
; 10) 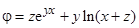 .
.
1.1.4. Вычислите  для следующих вариантов:
для следующих вариантов:
1) 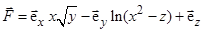 ; 2)
; 2)  ;
;
3) 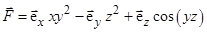 ; 4)
; 4) 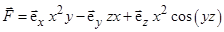 ;
;
5) 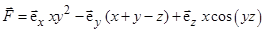 ; 6)
; 6) 
1.1.5. Вычислите 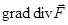 для следующих вариантов:
для следующих вариантов:
1)  ;
;
2) 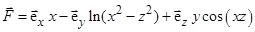 ;
;
3) 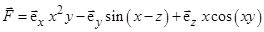 ;
;
4) 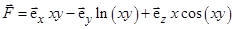 ;
;
5) 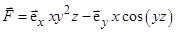 ;
;
6) 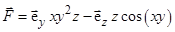 ;
;
7)  .
.
1.1.6. Найдите скалярное произведение полей  и
и  , заданных в различных системах координат. Результат представьте в системе координат, указанной в задании.
, заданных в различных системах координат. Результат представьте в системе координат, указанной в задании.
1) 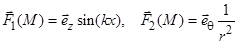 (сферические).
(сферические).
2) 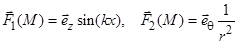 (декартовы).
(декартовы).
3) 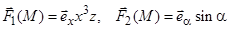 (декартовы).
(декартовы).
4) 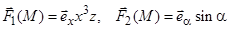 (цилиндрические).
(цилиндрические).
5)  (декартовы).
(декартовы).
6) 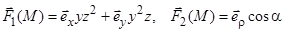 (цилиндрические).
(цилиндрические).
7)  (цилиндрические).
(цилиндрические).
8)  (цилиндрические).
(цилиндрические).
9)  (декартовы).
(декартовы).
10)  (цилиндрические).
(цилиндрические).
11)  (сферические).
(сферические).
12) 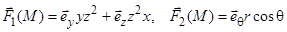 (сферические).
(сферические).
13) 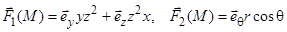 (декартовы).
(декартовы).
14)  (декартовы).
(декартовы).
1.1.7. Найдите векторное произведение полей  и
и  , заданных в различных системах координат. Результат представьте в системе координат, указанной в задании.
, заданных в различных системах координат. Результат представьте в системе координат, указанной в задании.
1)  (декартовы);
(декартовы);
2) 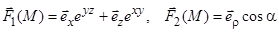 (декартовы);
(декартовы);
3) 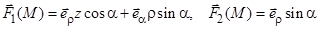 (цилиндрическая);
(цилиндрическая);
4) 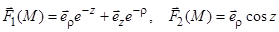 (цилиндрическая);
(цилиндрическая);
5) 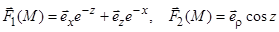 (цилиндрическая);
(цилиндрическая);
6) 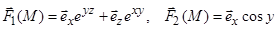 (декартовы);
(декартовы);
7)  (цилиндрическая);
(цилиндрическая);
8) 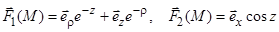 (декартовы);
(декартовы);
9) 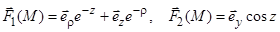 (декартовы);
(декартовы);
10) 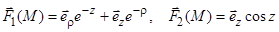 (декартовы);
(декартовы);
11) 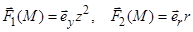 (декартовы);
(декартовы);
12) 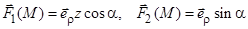 (цилиндрическая);
(цилиндрическая);
13) 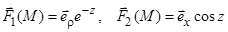 (декартовы);
(декартовы);
14)  (декартовы).
(декартовы).
1.1.8. Найдите поток векторного поля 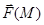 по поверхности S.
по поверхности S.
1) 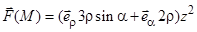 , S – полуцилиндр:
, S – полуцилиндр: 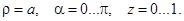 В качестве орта нормали к S выберете
В качестве орта нормали к S выберете  .
.
2) 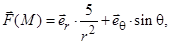 S – сфера:
S – сфера: 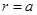 В качестве орта нормали к S выберете
В качестве орта нормали к S выберете  .
.
3) 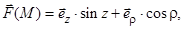 S – кольцевая поверхность:
S – кольцевая поверхность:  . В качестве орта нормали к S выберете
. В качестве орта нормали к S выберете 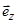 .
.
4) 
 В качестве орта нормали к S выберете
В качестве орта нормали к S выберете 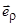 .
.
5) 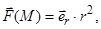
 В качестве орта нормали к S выберете
В качестве орта нормали к S выберете  .
.
6) 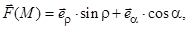
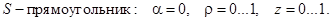 В качестве орта нормали к S выберете
В качестве орта нормали к S выберете  .
.
7) 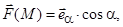
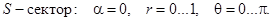 В качестве орта нормали к S выберете
В качестве орта нормали к S выберете  .
.
8) 
 В качестве орта нормали к S выберете
В качестве орта нормали к S выберете  .
.
9) 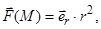
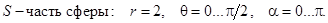 В качестве орта нормали к S выберете
В качестве орта нормали к S выберете  .
.
10) 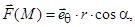
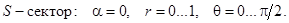 В качестве орта нормали к S выберете
В качестве орта нормали к S выберете  .
.
1.1.9. Найдите поток векторного произведения 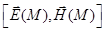 по поверхности S:
по поверхности S:
1)  . S – кольцевая поверхность:
. S – кольцевая поверхность: 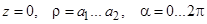 . В качестве орта нормали к S выберете
. В качестве орта нормали к S выберете 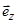 .
.
2)  . S – сфера:
. S – сфера:  . В качестве орта нормали к S выберете
. В качестве орта нормали к S выберете  .
.
3)  . S – полукольцо:
. S – полукольцо:  . В качестве орта нормали к S выберете
. В качестве орта нормали к S выберете 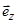 .
.
4) 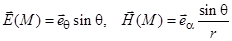 . S – сфера:
. S – сфера:  . В качестве орта нормали к S выберете
. В качестве орта нормали к S выберете  .
.
5) 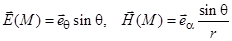 . S – сфера:
. S – сфера:  . В качестве орта нормали к S выберете
. В качестве орта нормали к S выберете  .
.
6) 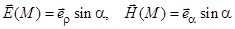 , S – кольцо:
, S – кольцо:  . В качестве орта нормали к S выберете
. В качестве орта нормали к S выберете 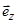 .
.
2. ЭЛЕКТРОСТАТИКА И МАГНИТОСТАТИКА
Теоретические сведения
Закон Гаусса в интегральной и дифференциальной формах:
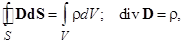
где 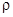 – объемная плотность электрического заряда;
– объемная плотность электрического заряда;  – вектор электрической индукции;
– вектор электрической индукции;  – вектор напряженности электрического поля;
– вектор напряженности электрического поля; 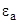 и
и 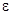 – абсолютная и относительная диэлектрическая проницаемость среды;
– абсолютная и относительная диэлектрическая проницаемость среды; 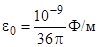 – диэлектрическая проницаемость вакуума; S – замкнутая поверхность, ограничивающая объем V. Напряженность электростатического поля
– диэлектрическая проницаемость вакуума; S – замкнутая поверхность, ограничивающая объем V. Напряженность электростатического поля  , где
, где  – скалярный электрический потенциал, удовлетворяющий уравнению Пуассона
– скалярный электрический потенциал, удовлетворяющий уравнению Пуассона

Граничные условия для векторов 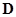 и
и  на границе раздела материальных сред
на границе раздела материальных сред

где σпов – плотность поверхностного заряда на границе раздела (поверхностный заряд может отсутствовать); вектор нормали направлен в сторону первой среды.
Электрический потенциал φ сохраняет постоянное значение на поверхности идеальных проводников; на границе раздела двух сред  .
.
Емкость системы двух проводников  где U – абсолютное значение разности потенциалов между проводниками. Энергия электрического поля в объеме V
где U – абсолютное значение разности потенциалов между проводниками. Энергия электрического поля в объеме V
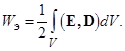
Закон полного тока в интегральной и дифференциальной формах:
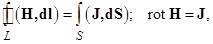
где J – вектор плотности электрического тока; H – вектор напряженности магнитного поля; L – замкнутый контур, ограничивающий поверхность S.
Вектор магнитной индукции  где μа и μ – абсолютная и относительная магнитная проницаемость среды, μ0=4π·10-7 Гн/м – магнитная проницаемость вакуума.
где μа и μ – абсолютная и относительная магнитная проницаемость среды, μ0=4π·10-7 Гн/м – магнитная проницаемость вакуума.
Вектора Н и B на границе раздела материальных сред удовлетворяют граничным условиям

где принято, что вектор нормали n направлен в сторону первой среды; J пов – вектор плотности поверхностного тока.
Магнитный поток, пронизывающий поверхность S 
Если по проводящему контуру (например, проволочному витку) протекает ток I, который создает поток Ф через поверхность, опирающуюся на контур, то индуктивность витка 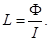 Индуктивность катушки с N витками
Индуктивность катушки с N витками 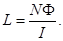
Энергия магнитного поля 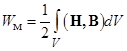 .
.
2.1 Электростатические поля
2.1.1. В точке с декартовыми координатами (-1 м, 0, 0) находится заряд q1 = 10 нКл, а в точке с координатами (1 м, 0, 0) – заряд q2 = 20 нКл. Определите напряженность электрического поля в точках А и В с координатами (0,0,0) и (2 м, 0, 0). Заряды расположены в вакууме.
2.1.2. В точках с декартовыми координатами (-1 м, 0, 0) и (1 м, 0, 0) находятся заряды 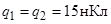 . Определите напряженность электрического поля в точках А и В с координатами (0, 1 м, 0) и (1 м, 1 м, 0). Заряды расположены в вакууме.
. Определите напряженность электрического поля в точках А и В с координатами (0, 1 м, 0) и (1 м, 1 м, 0). Заряды расположены в вакууме.
2.1.3. Плоскость z = 0 равномерно заряжена с поверхностной плотностью электрического заряда 01 нКл/м2. Определите поля Е и D во всем пространстве, считая, что заряды находятся в вакууме.
2.1.4. Плоскости z = 0 и z = 0,5 м равномерно заряжены с одинаковой поверхностной плотностью электрического заряда 0,05 нКл/м2. Абсолютная диэлектрическая проницаемость среды равна ε0. Определите векторы Е и D во всем пространстве.
2.1.5. Разность потенциалов между пластинами плоского воздушного конденсатора равна 1 В. Определите плотность поверхностного заряда на обкладках, считая, что эффектами искажения поля около края пластин можно пренебречь. Расстояние между обкладками 5 мм.
2.1.6. Между пластинами плоского конденсатора находится двухслойный диэлектрик. Толщина слоев d1 = 2 мм, d2 = 5 мм; относительные диэлектрические проницаемости слоев ε1 = 2, ε2 = 3. Площадь пластин 25 см2, расстояние между ними d = d1+d2. На верхней пластине равномерно распределен заряд q A = 10-9 Кл, на нижней пластине – заряд qB = -qA. Определите напряженность электрического поля в конденсаторе и разность потенциалов между пластинами. Считайте, что эффектами искажения поля около края пластин можно пренебречь.
2.1.7. Между пластинами плоского конденсатора находится двухслойный диэлектрик. Толщина слоев d1 и d2, относительная диэлектрическая проницаемость слоев ε1 и ε2. Площадь пластин S, расстояние между пластинами d = d1+d2. Получите выражение для емкости данного конденсатора, считая, что эффектами искажения поля около края пластин можно пренебречь. Вычислите емкость конденсатора, используя данные задачи 2.1.6.
2.1.8. Бесконечно протяженный плоский слой толщиной d равномерно заряжен с объемной плотностью ρ0. Абсолютные диэлектрические проницаемости среды, находящейся внутри и вне слоя, одинаковы и равны ε0. Определите напряженность электрического поля во всем пространстве. Считайте, что слой расположен в области -d/2< z <d/2.
2.1.9. Бесконечно длинный цилиндр радиусом 1 см равномерно заряжен с поверхностной плотностью 10-9 Кл/м2. Пространство, окружающее цилиндр, заполнено воздухом. Определите напряженность электрического поля на расстоянии 20 см от оси цилиндра.
2.1.10. Два бесконечно длинных коаксиальных цилиндра имеют радиусы a = 2 см и b = 4 см (рис. 2.1). Внутренний цилиндр равномерно заряжен с поверхностной плотностью 0,1 мкКл/м2, наружный цилиндр заряжен с плотностью -0,1 мкКл/м. Пространство между цилиндрами заполнено воздухом, потенциал наружного цилиндра равен нулю. Определите распределение потенциала и напряженности электрического поля в пространстве между цилиндрами.
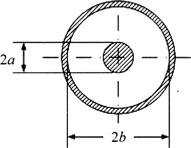
Рис. 2.1 Коаксиальная линия передачи.
2.1.11. Коаксиальная линия передачи образована двумя бесконечно длинными металлическими цилиндрами с радиусами а и b (b>а, рис. 2.1). Между цилиндрами находится среда с относительной диэлектрической проницаемостью с. Получите выражение для погонной емкости данной линии передачи.
2.1.12. Внутри бесконечно длинной цилиндрической области радиусом r 0 равномерно распределен электрический заряд с объемной плотностью ρ0. Абсолютные диэлектрические проницаемости внутренней и внешней областей равны εa1 и εа2 соответственно. Определите напряженность электрического поля во всем пространстве.
2.1.13. На поверхности металлического шара радиусом 10 см равномерно распределен электрический заряд. Шар окружен воздухом. Определите поверхностную плотность заряда, если на расстоянии 20 см от центра шара напряженность электрического поля составляет 50 В/м.
2.1.14. Сферический конденсатор образован двумя концентрическими металлическими сферами с радиусами а и b (а < b). Между сферами находится диэлектрик с относительной диэлектрической проницаемостью ε. Получите выражение для емкости данного конденсатора.
2.1.15. Сферический конденсатор образован двумя концентрическими металлическими сферами с радиусами а и b (а< b). Между сферами находится двухслойный диэлектрик. Первый сферический слой ограничен радиусами а и с (с > а) и имеет относительную диэлектрическую проницаемость ε1 второй слой ограничен радиусами с и b (b > с) и имеет относительную диэлектрическую проницаемость ε2. Получите выражение для емкости данного конденсатора.
2.1.16. Внутри сферической области радиусом а равномерно распределен электрический заряд с объемной плотностью ρ0. Абсолютные диэлектрические проницаемости области и окружающей среды одинаковы и равны ε0. Определите напряженность электрического поля во всем пространстве.
2.2. Стационарные магнитные поля
2.2.1. В плоскости x = 0 протекает постоянный ток с равномерно распределенной поверхностной плотностью J пов= J0· e z. Определите напряженность магнитного поля во всем пространстве.
2.2.2. В плоскости x = 0 и плоскости x = d протекают постоянные токи с одинаковыми поверхностными плотностями J пов = J0· e y. Определите напряженность магнитного поля во всем пространстве.
2.2.3. В бесконечном проводящем слое толщиной d протекает постоянный ток с равномерно распределенной плотностью J = J0· e z (используется декартова система координат, в которой ось x направлена по направлению нормали к поверхности слоя). Определите напряженность магнитного поля во всем пространстве. Считайте, что слой расположен в области -d/2 < x < d/2.
2.2.4. По бесконечному цилиндрическому проводнику радиусом 2 мм протекает постоянный ток. Напряженность магнитного поля на поверхности проводника составляет 10 А/м. Определите плотность тока в проводнике.
2.2.5. По бесконечному цилиндрическому проводнику радиусом а протекает постоянный ток с плотностью J0, которая равномерно распределена в пределах поперечного сечения проводника. Определите напряженность магнитного поля внутри и вне проводника.
2.2.6. Бесконечный цилиндрический слой ограничен двумя цилиндрическими поверхностями с радиусами а и b (а < b). По данному слою протекает постоянный ток с плотностью J0. Определите напряженность магнитного поля во всем пространстве.
2.2.7. Коаксиальная линия передачи образована двумя соосными металлическими цилиндрами радиусами а и b (а<Ь, рис. 2.1). Среда, заполняющая пространство между цилиндрами, имеет относительную магнитную проницаемость μ. Выведите формулу для расчёта погонной индуктивности линии передачи.
2.2.8. На кольцевом сердечнике из ферромагнитного материала с μ = 100 размещено 50 витков провода. Сердечник представляет собой цилиндрический слой высотой h = 6 мм, ограниченный цилиндрическими поверхностями радиусами а = 6 мм и b = 12 мм. По обмотке протекает ток 0,1 А. Определите минимальное и максимальное значение индукции в сердечнике.
2.2.9. На кольцевом сердечнике из ферромагнитного материала с μ >> 1 размещено N витков провода. Сердечник представляет собой цилиндрический слой высотой h, ограниченный цилиндрическими поверхностями радиусами а и b (а < b). Выведите формулу для расчёта индуктивности данной катушки. При выводе учитывайте, что магнитная проницаемость сердечника велика, и потоком магнитного поля вне сердечника можно пренебречь.
3. ОСНОВНЫЕ ПОЛОЖЕНИЯ ЭЛЕКТРОДИНАМИКИ
Теоретические сведения
1. Закон Ампера-Максвелла 
2. Закон Фарадея  .
.
3. Закон Гаусса  .
.
Здесь в уравнениях 1 и 2 замкнутый контур L ограничивает поверхность S; с конца векторного элемента поверхности dS движение вдоль контура наблюдается в направлении против часовой стрелки. В уравнениях 3 замкнутая поверхность S ограничивает объем V; векторный элемент поверхности dS ориентирован в направлении внешней нормали к S. В уравнении 1 J – плотность электрического тока.
Уравнения Максвелла в дифференциальной форме:
1. 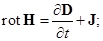
2. 
3. 
4. 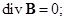
5. 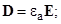
6. 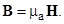
Уравнения Максвелла в дифференциальной форме для комплексных амплитуд полей (случай гармонических колебаний):
1. 
2. 
3. 
4. 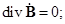
5. 
6. 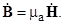
Связь между мгновенными значениями вектора, гармонически изменяющегося во времени, и его комплексной амплитудой записывается в виде 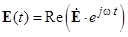 .
.
Закон сохранения заряда в интегральной и дифференциальной формах

где J – плотность электрического тока.
Если среда анизотропная и характеризуется тензором абсолютной диэлектрической проницаемости 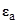 , то материальное уравнение 5 записывается в виде
, то материальное уравнение 5 записывается в виде
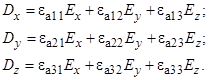
Аналогично записывается уравнение 6 в случае, когда анизотропная среда характеризуется тензором абсолютной магнитной проницаемости μа.
Вектор Пойтинга

Вектор Пойнтинга для комплексных амплитуд гармонических колебаний
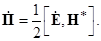
Теорема Пойнтинга для мгновенных мощностей в интегральной форме

где 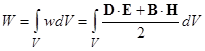 – энергия электромагнитного поля в объёме V, ограниченном замкнутой поверхностью S, w – плотность энергии электромагнитного поля;
– энергия электромагнитного поля в объёме V, ограниченном замкнутой поверхностью S, w – плотность энергии электромагнитного поля;
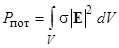 – мощность тепловых потерь в объёмеV;
– мощность тепловых потерь в объёмеV; 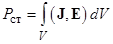 – мощность сторонних источников в объеме V.
– мощность сторонних источников в объеме V.
Нормальные составляющие векторов D и В на границе раздела материальных сред удовлетворяют граничным условиям
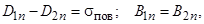
где 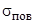 – плотность поверхностного заряда на границе раздела; вектор нормали направлен в сторону первой среды.
– плотность поверхностного заряда на границе раздела; вектор нормали направлен в сторону первой среды.
Касательные составляющие векторов Е и Н на границе раздела материальных сред удовлетворяют граничным условиям
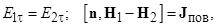
где n – единичный вектор нормали, направленный в сторону первой среды; J пов – вектор плотности поверхностного тока.
Если одной из сред является идеальный проводник (σ = ∞), то на его поверхности


где единичный вектор нормали n направлен в сторону от идеального проводника.
3.1. Уравнения Максвелла
3.1.1. В некоторой точке пространства комплексная амплитуда вектора напряженности электрического поля
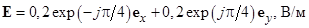
Определите мгновенные значения вектора Е в моменты времени t1 = 0,125 мкс и t2 = 0,375 мкс, если частота колебаний равна 1 МГц.
3.1.2. Запишите выражение для вектора напряженности магнитного поля 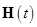 , имеющего линейную поляризацию в плоскости XOZ. Колебания вектора Н происходят с амплитудой 10 мА/м вдоль прямой, наклоненной под углом 30° к оси z, и углом 60° к оси х. При t = 0 проекция Hz = 5 мА/м. Частота колебаний 2 ГГц.
, имеющего линейную поляризацию в плоскости XOZ. Колебания вектора Н происходят с амплитудой 10 мА/м вдоль прямой, наклоненной под углом 30° к оси z, и углом 60° к оси х. При t = 0 проекция Hz = 5 мА/м. Частота колебаний 2 ГГц.
3.1.3. Запишите выражения для вектора электрического поля E (t) и для его комплексной амплитуды Е. Вектор Е имеет круговую поляризацию в плоскости YOZ, и вращается в направлении часовой стрелки, если смотреть с конца единичного вектора е х, Амплитуда колебаний проекции Еу равна 5 мВ/м, частота колебаний 100 МГц. В момент времени t = 0 вектор Е повернут под углом 45° к осям у и z.
3.1.4. В диэлектрике с относительной проницаемостью 3,8 и удельной проводимостью 0,023 см/м комплексная амплитуда 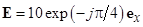 мВ/м. Определите комплексные амплитуды векторов плотности тока проводимости, тока смещения и полного тока. Частота колебаний 150 МГц.
мВ/м. Определите комплексные амплитуды векторов плотности тока проводимости, тока смещения и полного тока. Частота колебаний 150 МГц.
3.1.5. В среде с относительной диэлектрической проницаемостью 4 колебания плотности полного тока опережают по фазе колебания плотности тока проводимости на 73,3°. Определите удельную проводимость среды, если частота равна 15 МГц.
3.1.6. Рамочная антенна, представляющая собой проволочную петлю площадью S = 0,1 м2, находится в переменном электромагнитном поле. Комплексная амплитуда вектора напряженности магнитного поля не изменяется в пределах петли и равна 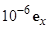 А/м. Частота колебаний 100 МГц, окружающая среда – воздух. При какой ориентации антенны амплитуда ЭДС, наведенной в петле, будет максимальной. Определите амплитуду ЭДС для этой ориентации.
А/м. Частота колебаний 100 МГц, окружающая среда – воздух. При какой ориентации антенны амплитуда ЭДС, наведенной в петле, будет максимальной. Определите амплитуду ЭДС для этой ориентации.
3.1.7. К плоскому конденсатору с площадью пластин Sn приложено напряжение 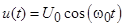 . Между пластинами находится слой диэлектрика толщиной d, имеющего относительную проницаемость ε. Получите выражение для тока смещения, протекающего через конденсатор двумя способами: а) проинтегрировав плотность тока смещения; б) воспользовавшись известной формулой для ёмкости плоского конденсатора
. Между пластинами находится слой диэлектрика толщиной d, имеющего относительную проницаемость ε. Получите выражение для тока смещения, протекающего через конденсатор двумя способами: а) проинтегрировав плотность тока смещения; б) воспользовавшись известной формулой для ёмкости плоского конденсатора 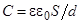 .
.
3.1.8. К плоскому конденсатору приложено напряжение с амплитудой 0,5 В и частотой 300 кГц. Между обкладками конденсатора находятся слой диэлектрика, имеющий толщину 3 мм, относительную проницаемость 2,5 и удельную проводимость 2,5·10-6 см/м. Определите амплитуду колебаний плотности тока смещения и плотности тока проводимости в конденсаторе. Найдите разность фаз колебаний напряжения и плотности полного тока в конденсаторе.
3.1.9. К плоскому конденсатору приложено гармоническое напряжение с частотой 10 МГц. Между пластинами находится диэлектрик с относительной проницаемостью 3,3 и неизвестной удельной проводимостью. Определите удельную проводимость, если амплитуда тока смещения в 104 раз больше амплитуды тока проводимости.
3.1.10*. В момент времени t = 0 в однородной проводящей среде с относительной диэлектрической проницаемостью ε и удельной проводимостью σ создано пространственное распределение объёмной плотности заряда 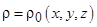 . За счёт протекания токов проводимости ρ будет уменьшаться со временем при t>0. Определите закон уменьшения плотности объёмного заряда.
. За счёт протекания токов проводимости ρ будет уменьшаться со временем при t>0. Определите закон уменьшения плотности объёмного заряда.
3.1.11*. Пользуясь вторым уравнением Максвелла в дифференциальной форме, выведите четвёртое уравнение Максвелла (рассмотрите случай гармонических колебаний).
3.1.12*. Пользуясь первым уравнением Максвелла в дифференциальной форме и уравнением непрерывности, выведите третье уравнение Максвелла (рассмотрите случай гармонических колебаний).
3.1.13. Запишите первое и третье уравнения Максвелла в дифференциальной форме для составляющих векторов поля в цилиндрической системе координат (рассмотрите случай гармонических колебаний).
3.1.14. 3апишите второе и четвертое уравнения Максвелла в дифференциальной форме для составляющих векторов поля в сферической системе координат (рассмотрите случай гармонических колебаний).
3.1.15. Электромагнитная волна распространяется вдоль оси z, причем составляющие поля не зависят от поперечных координат х, у. Пользуясь уравнениями Максвелла для комплексных амплитуд, докажите, что у такой волны отсутствуют продольные составляющие Ez, Нz.
3.1.16. Некоторый анизотропный диэлектрик характеризуется в декартовой системе координат тензором относительной диэлектрической проницаемости
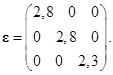
Найдите угол в пространстве между векторами Е и D для двух случаев: а) E = 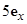 В/м; б) E =
В/м; б) E = 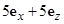 В/м.
В/м.
3.1.17*. Комплексная амплитуда вектора напряженности магнитного поля в воздухе
 мА/м
мА/м
(случай плоской волны, распространяющейся вдоль оси у). Сторонние токи отсутствуют. Определите комплексную амплитуду вектора напряженности электрического поля и частоту колебаний.
3.1.18. Комплексная амплитуда вектора напряженности магнитного поля в воздухе
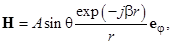
где А и φ – вещественные константы (используется сферическая система координат). Сторонние токи отсутствуют, частота колебаний равна ω0. Определите комплексную амплитуду вектора напряженности электрического поля.
3.1.19. Пользуясь уравнениями Максвелла, определите, возможно ли существование в однородной изотропной среде переменного электромагнитного поля, в котором векторы Е и Н параллельны одной и той же декартовой оси. Сторонние токи отсутствуют.
3.1.20*. Электромагнитный процесс в однородной изотропной среде без потерь имеет отличные от нуля составляющие Ёх и Ну, которые зависят только от координаты z. Среда характеризуется абсолютными проницаемостями еа и |ia. Частота колебаний со, сторонние токи отсутствуют. Пользуясь уравнениями Максвелла, получите дифференциальные уравнения второго порядка для Ёх и Ну. Определите общий вид решения данных обыкновенных дифференциальных уравнений и получите характеристическое уравнение – условие существования ненулевого поля.
3.1.21*. Пользуясь уравнениями Максвелла, докажите, что сферически симметричное распределение тока с плотностью J = J(r)er не возбуждает магнитного поля.
3.1.22*. В плоскости z = 0 в момент времени t = 0 включается равномерно распределенный постоянный ток с поверхностной плотностью J пов = J 0 e y. Окружающая среда – воздух. С помощью уравнений Максвелла в интегральной форме определите поля Е и Н во всем пространстве. При решении учитывайте, что процесс установления постоянных уровней полей Е и H в пространстве представляет собой импульсную волну. Плоский фронт этой волны распространяется со скоростью v = v e z при z> 0 и v = - v e z при z < 0. Покажите, что 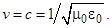
3.2. Энергетические соотношения в электродинамике
3.2.1. В некоторой точке пространства заданы комплексные амплитуды векторов электромагнитного поля
а) 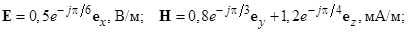
б) 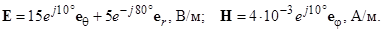
Определите среднее значение вектора Пойнтинга.
3.2.2. В заданной точке пространства средняя плотность потока мощности равна 0,1 Вт/м2. Вектор напряженности электрического поля ориентирован параллельно оси х и характеризуется амплитудой колебаний 3 В/м (колебания гармонические). Вектор напряженности магнитного поля ориентирован параллельно оси у. Определите амплитуду колебаний вектора H, если колебания вектора H отстают по фазе на 15° от колебаний






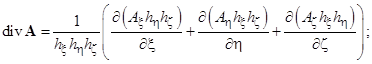
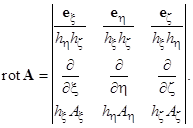
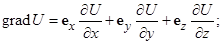

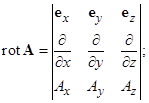


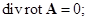

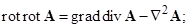
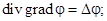

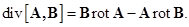


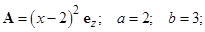
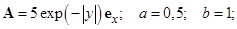
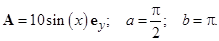

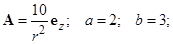



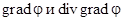 для следующих вариантов:
для следующих вариантов: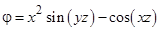 ; 2)
; 2) 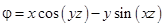 ;
;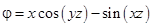 ; 4)
; 4)  ;
;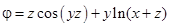 ; 6)
; 6) 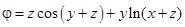 ;
;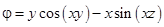 ; 8)
; 8) 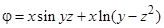 ;
;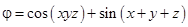 ; 10)
; 10) 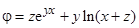 .
. для следующих вариантов:
для следующих вариантов: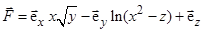 ; 2)
; 2)  ;
;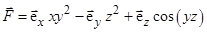 ; 4)
; 4) 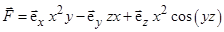 ;
;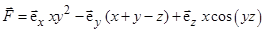 ; 6)
; 6) 
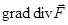 для следующих вариантов:
для следующих вариантов: ;
;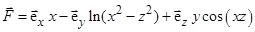 ;
;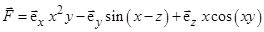 ;
;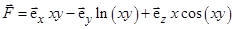 ;
;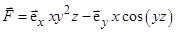 ;
;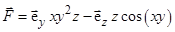 ;
; .
. и
и  , заданных в различных системах координат. Результат представьте в системе координат, указанной в задании.
, заданных в различных системах координат. Результат представьте в системе координат, указанной в задании.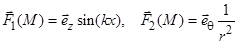 (сферические).
(сферические).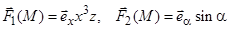 (декартовы).
(декартовы). (декартовы).
(декартовы).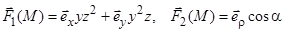 (цилиндрические).
(цилиндрические). (цилиндрические).
(цилиндрические). (декартовы).
(декартовы). (цилиндрические).
(цилиндрические).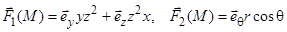 (сферические).
(сферические). (декартовы).
(декартовы). (декартовы);
(декартовы);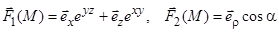 (декартовы);
(декартовы);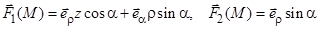 (цилиндрическая);
(цилиндрическая);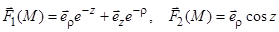 (цилиндрическая);
(цилиндрическая);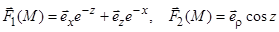 (цилиндрическая);
(цилиндрическая);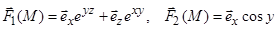 (декартовы);
(декартовы); (цилиндрическая);
(цилиндрическая);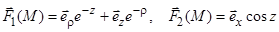 (декартовы);
(декартовы);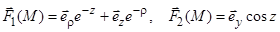 (декартовы);
(декартовы);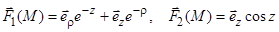 (декартовы);
(декартовы);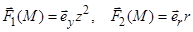 (декартовы);
(декартовы);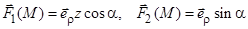 (цилиндрическая);
(цилиндрическая);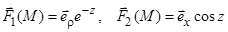 (декартовы);
(декартовы); (декартовы).
(декартовы).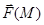 по поверхности S.
по поверхности S.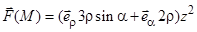 , S – полуцилиндр:
, S – полуцилиндр: 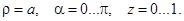 В качестве орта нормали к S выберете
В качестве орта нормали к S выберете 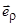 .
.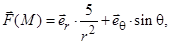 S – сфера:
S – сфера: 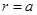 В качестве орта нормали к S выберете
В качестве орта нормали к S выберете  .
.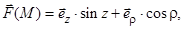 S – кольцевая поверхность:
S – кольцевая поверхность:  . В качестве орта нормали к S выберете
. В качестве орта нормали к S выберете 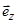 .
.
 В качестве орта нормали к S выберете
В качестве орта нормали к S выберете 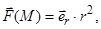
 В качестве орта нормали к S выберете
В качестве орта нормали к S выберете 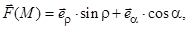
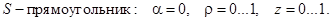 В качестве орта нормали к S выберете
В качестве орта нормали к S выберете  .
.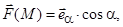
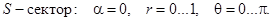 В качестве орта нормали к S выберете
В качестве орта нормали к S выберете 
 В качестве орта нормали к S выберете
В качестве орта нормали к S выберете 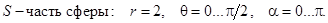 В качестве орта нормали к S выберете
В качестве орта нормали к S выберете 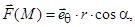
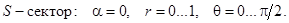 В качестве орта нормали к S выберете
В качестве орта нормали к S выберете 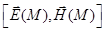 по поверхности S:
по поверхности S: . S – кольцевая поверхность:
. S – кольцевая поверхность: 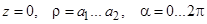 . В качестве орта нормали к S выберете
. В качестве орта нормали к S выберете  . S – сфера:
. S – сфера:  . В качестве орта нормали к S выберете
. В качестве орта нормали к S выберете  . S – полукольцо:
. S – полукольцо:  . В качестве орта нормали к S выберете
. В качестве орта нормали к S выберете 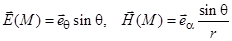 . S – сфера:
. S – сфера: 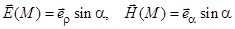 , S – кольцо:
, S – кольцо:  . В качестве орта нормали к S выберете
. В качестве орта нормали к S выберете 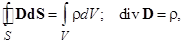
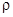 – объемная плотность электрического заряда;
– объемная плотность электрического заряда;  – вектор электрической индукции;
– вектор электрической индукции;  – вектор напряженности электрического поля;
– вектор напряженности электрического поля; 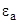 и
и 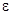 – абсолютная и относительная диэлектрическая проницаемость среды;
– абсолютная и относительная диэлектрическая проницаемость среды; 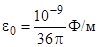 – диэлектрическая проницаемость вакуума; S – замкнутая поверхность, ограничивающая объем V. Напряженность электростатического поля
– диэлектрическая проницаемость вакуума; S – замкнутая поверхность, ограничивающая объем V. Напряженность электростатического поля  , где
, где  – скалярный электрический потенциал, удовлетворяющий уравнению Пуассона
– скалярный электрический потенциал, удовлетворяющий уравнению Пуассона
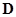 и
и 
 .
. где U – абсолютное значение разности потенциалов между проводниками. Энергия электрического поля в объеме V
где U – абсолютное значение разности потенциалов между проводниками. Энергия электрического поля в объеме V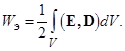
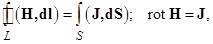
 где μа и μ – абсолютная и относительная магнитная проницаемость среды, μ0=4π·10-7 Гн/м – магнитная проницаемость вакуума.
где μа и μ – абсолютная и относительная магнитная проницаемость среды, μ0=4π·10-7 Гн/м – магнитная проницаемость вакуума.

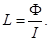 Индуктивность катушки с N витками
Индуктивность катушки с N витками 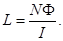
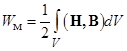 .
.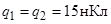 . Определите напряженность электрического поля в точках А и В с координатами (0, 1 м, 0) и (1 м, 1 м, 0). Заряды расположены в вакууме.
. Определите напряженность электрического поля в точках А и В с координатами (0, 1 м, 0) и (1 м, 1 м, 0). Заряды расположены в вакууме.

 .
. .
.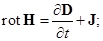


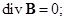
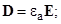
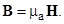



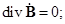

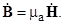
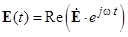 .
.
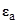 , то материальное уравнение 5 записывается в виде
, то материальное уравнение 5 записывается в виде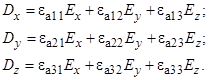

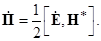

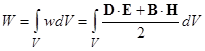 – энергия электромагнитного поля в объёме V, ограниченном замкнутой поверхностью S, w – плотность энергии электромагнитного поля;
– энергия электромагнитного поля в объёме V, ограниченном замкнутой поверхностью S, w – плотность энергии электромагнитного поля;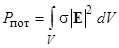 – мощность тепловых потерь в объёмеV;
– мощность тепловых потерь в объёмеV; 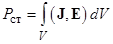 – мощность сторонних источников в объеме V.
– мощность сторонних источников в объеме V.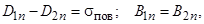
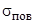 – плотность поверхностного заряда на границе раздела; вектор нормали направлен в сторону первой среды.
– плотность поверхностного заряда на границе раздела; вектор нормали направлен в сторону первой среды.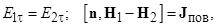


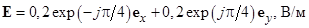
 , имеющего линейную поляризацию в плоскости XOZ. Колебания вектора Н происходят с амплитудой 10 мА/м вдоль прямой, наклоненной под углом 30° к оси z, и углом 60° к оси х. При t = 0 проекция Hz = 5 мА/м. Частота колебаний 2 ГГц.
, имеющего линейную поляризацию в плоскости XOZ. Колебания вектора Н происходят с амплитудой 10 мА/м вдоль прямой, наклоненной под углом 30° к оси z, и углом 60° к оси х. При t = 0 проекция Hz = 5 мА/м. Частота колебаний 2 ГГц.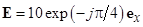 мВ/м. Определите комплексные амплитуды векторов плотности тока проводимости, тока смещения и полного тока. Частота колебаний 150 МГц.
мВ/м. Определите комплексные амплитуды векторов плотности тока проводимости, тока смещения и полного тока. Частота колебаний 150 МГц.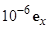 А/м. Частота колебаний 100 МГц, окружающая среда – воздух. При какой ориентации антенны амплитуда ЭДС, наведенной в петле, будет максимальной. Определите амплитуду ЭДС для этой ориентации.
А/м. Частота колебаний 100 МГц, окружающая среда – воздух. При какой ориентации антенны амплитуда ЭДС, наведенной в петле, будет максимальной. Определите амплитуду ЭДС для этой ориентации.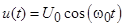 . Между пластинами находится слой диэлектрика толщиной d, имеющего относительную проницаемость ε. Получите выражение для тока смещения, протекающего через конденсатор двумя способами: а) проинтегрировав плотность тока смещения; б) воспользовавшись известной формулой для ёмкости плоского конденсатора
. Между пластинами находится слой диэлектрика толщиной d, имеющего относительную проницаемость ε. Получите выражение для тока смещения, протекающего через конденсатор двумя способами: а) проинтегрировав плотность тока смещения; б) воспользовавшись известной формулой для ёмкости плоского конденсатора 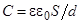 .
.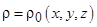 . За счёт протекания токов проводимости ρ будет уменьшаться со временем при t>0. Определите закон уменьшения плотности объёмного заряда.
. За счёт протекания токов проводимости ρ будет уменьшаться со временем при t>0. Определите закон уменьшения плотности объёмного заряда.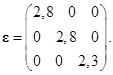
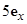 В/м; б) E =
В/м; б) E = 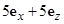 В/м.
В/м. мА/м
мА/м