5.2.1. Плоская электромагнитная волна падает по нормали из вакуума на границу раздела с металлом, у которого μ = 1 и удельная проводимость составляет 1,5·10 См/м. Частота колебаний равна 500 МГц. Определите какая часть плотности мощности падающей волны расходуется на нагрев металла.
5.2.2*. Плоская электромагнитная волна падает по нормали из воздух на границу раздела с металлом, характеризующимся удельной проводимостью σ и относительной магнитной проницаемостью μ = 1 Частота колебаний ω. Получите приближенное выражение для коэффициента отражения.
5.2.3*. Плоская электромагнитная волна с амплитудой магнитног вектора  падает по нормали из воздуха на границу раздела с металлом, характеризующимся удельной проводимостью σ и относительной магнитной проницаемостью μ = 1. Частота колебаний ω. Получите выражение для амплитуды магнитного вектора на поверхности металла
падает по нормали из воздуха на границу раздела с металлом, характеризующимся удельной проводимостью σ и относительной магнитной проницаемостью μ = 1. Частота колебаний ω. Получите выражение для амплитуды магнитного вектора на поверхности металла  . Найдите отношение
. Найдите отношение  для частоты 3 ГГц и удельной проводимости 5,7·10 См/м (медь).
для частоты 3 ГГц и удельной проводимости 5,7·10 См/м (медь).
5.2.4. Плоская электромагнитная волна с амплитудой электрического вектора 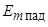 падает по нормали из воздуха на границу раздела с металлом, характеризующимся удельной проводимостью σ и относительной магнитной проницаемостью μ = 1. Частота колебаний ω. Получите выражение для амплитуды электрического вектора на поверхности металла
падает по нормали из воздуха на границу раздела с металлом, характеризующимся удельной проводимостью σ и относительной магнитной проницаемостью μ = 1. Частота колебаний ω. Получите выражение для амплитуды электрического вектора на поверхности металла  двумя способами: а) пользуясь граничными условиями Леонтовича; б) пользуясь приближенным выражением для коэффициента отражения при нормальном падении на реальный металл (задача 5.2.2.). Найдите отношение
двумя способами: а) пользуясь граничными условиями Леонтовича; б) пользуясь приближенным выражением для коэффициента отражения при нормальном падении на реальный металл (задача 5.2.2.). Найдите отношение  для частоты 1,5 ГГц и удельной проводимости 3·10 См/м.
для частоты 1,5 ГГц и удельной проводимости 3·10 См/м.
5.2.5. Плоская электромагнитная волна с амплитудой электрического вектора 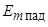 и амплитудой магнитного вектора
и амплитудой магнитного вектора  падает по нормали из воздуха на границу раздела с металлом, характеризующимся удельной проводимостью σ и относительной магнитной проницаемостью μ = 1. Частота колебаний ω. Получите выражения для коэффициентов прохождения полей Е и Н в металл на глубину l, которые определяются так:
падает по нормали из воздуха на границу раздела с металлом, характеризующимся удельной проводимостью σ и относительной магнитной проницаемостью μ = 1. Частота колебаний ω. Получите выражения для коэффициентов прохождения полей Е и Н в металл на глубину l, которые определяются так:  ,
, 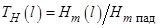 (здесь E(l) и H(l) – амплитуды электрического и магнитного векторов на расстоянии l от границы раздела).
(здесь E(l) и H(l) – амплитуды электрического и магнитного векторов на расстоянии l от границы раздела).
5.2.6. Плоская электромагнитная волна падает по нормали из воздуха на границу раздела с металлом, характеризующимся удельной приводимость σ и относительной магнитной проницаемостью μ = 1. Частота колебаний ω. Определите ослабление Δ плотности потока мощности в металле на глубине d в децибелах, где Δ = 10lg(Пcp.пр/Пср.пад); Пср.пад – плотность потока мощности в падающей волне; Пср.пр – плотность потока мощности в преломленной волне на глубине d. Запишите выражение для Δ в виде суммы двух слагаемых, одно из которых описывает потери мощности при отражении с поверхности металла, а другое – поглощение мощности в металле.
5.2.7. Решите предыдущую задачу для случая нормального падения электромагнитной волны с частотой 1 ГГц на границу раздела с медью. Определите ослабление плотности потока мощности на глубине 0,1 мм.
5.2.8. Плоская электромагнитная волна с параллельной поляризацией падает из воздуха под углом 30° на границу раздела с металлом, у которого μ = l и удельная проводимость составляет 2·107 См/м. Амплитуда напряженности электрического поля падающей волны 10 В/м, частота колебаний 3 ГГц. Определите амплитуду касательных составляющих векторов напряженности электрического и магнитного полей на поверхности металла.
5.2.9. Решите предыдущую задачу, считая, что падающая волна имеет перпендикулярную поляризацию.
5.2.10. Плоская электромагнитная волна с перпендикулярной поляризацией падает из воздуха под углом 60° на границу раздела с металлом, у которого μ = 1 и удельная проводимость составляет 3·107 См/м. Амплитуда напряженности электрического поля падающей волны 20 В/м, частота колебаний 10 ГГц. Определите плотность потока мощности прошедшей волны на границе раздела.
5.2.11. Плоская электромагнитная волна с параллельной поляризацией падает из воздуха под углом 45° на границу раздела с металлом, у которого μ = 1 и удельная проводимость составляет 5·10 См/м. Плотность потока мощности падающей волны 10 Вт/м2, частота колебаний 300 МГц. Определите удельную мощность тепловых потерь, приходящуюся на 1 м2 поверхности металла.
5.2.12. Плоская электромагнитная волна с параллельной поляризацией падает из воздуха под углом 50° на поверхность латуни. Найдите частоту, на которой мощность тепловых потерь, приходящаяся на 1 м2 поверхности латуни, составляет 10-n от мощности волны, падающей на 1 м2 этой поверхности. Решите эту задачу для двух случаев: а) n = 3; б) n = 4.
5.2.13. Плоская электромагнитная волна с перпендикулярной поляризацией падает из воздуха под углом 40° на границу раздела с металлом, у которого μ = 1 и удельная проводимость составляет 4·107 См/м. Амплитуда касательной составляющей электрического вектора на поверхности металла равна 2·10-3 В/м, частота колебаний f = 10 ГГц. Определите амплитуду электрического и магнитного векторов в падающей волне.
5.2.14*. Плоская электромагнитная волна с перпендикулярной поляризацией падает из воздуха под углом φ на границу раздела с металлом у которого μ = 1 и удельная проводимость равна σ. Пользуясь граничными условиями Леонтовича, получите приближенные выражения дл коэффициентов отражения и преломления по электрическому полю. Частот колебаний ω.
5.2.15*. Решите предыдущую задачу, считая, что падающая волна имеет параллельную поляризацию.
5.2.16*. Плоская электромагнитная волна с частотой колебаний ω падает из воздуха на границу раздела с металлом, у которого μ = 1 и удельная проводимость равна σ. Амплитуда касательной составляющей магнитного вектора на поверхности металла  . Получите выражение для мощности потерь, приходящейся на 1 м2 поверхности металла двумя способами: а) определив плотность потока мощности волны, проникнувшей в металл; б) воспользовавшись объемной плотностью мощности тепловых потерь внутри металла.
. Получите выражение для мощности потерь, приходящейся на 1 м2 поверхности металла двумя способами: а) определив плотность потока мощности волны, проникнувшей в металл; б) воспользовавшись объемной плотностью мощности тепловых потерь внутри металла.
5.2.17*. Как известно, объемные токи проводимости с плотность  протекают в достаточно тонком слое у поверхности реального проводника с удельной проводимостью σ и абсолютной магнитной проницаемостью μа. При этом для определения касательной к поверхности проводника составляющей магнитного вектора
протекают в достаточно тонком слое у поверхности реального проводника с удельной проводимостью σ и абсолютной магнитной проницаемостью μа. При этом для определения касательной к поверхности проводника составляющей магнитного вектора  можно по аналогии с идеальным проводником ввести эквивалентный квазиповерхностный ток с плотностью
можно по аналогии с идеальным проводником ввести эквивалентный квазиповерхностный ток с плотностью 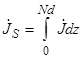 , где
, где 
 толщина скин-слоя. Покажите, что
толщина скин-слоя. Покажите, что  . Получите выражение, связывающее
. Получите выражение, связывающее 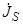 с комплексной амплитудой касательной составляющей электрического поля поверхности металла
с комплексной амплитудой касательной составляющей электрического поля поверхности металла 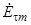 .
.
5.2.18*. Через поперечное сечение цилиндрического проводню диаметром D протекает полный ток с комплексной амплитудой  . По определению, погонным внутренним импедансом провода называется отношение касательной составляющей электрического вектора на поверхности провода к полному току:
. По определению, погонным внутренним импедансом провода называется отношение касательной составляющей электрического вектора на поверхности провода к полному току:  . Получите выражения для погонного активного сопротивления
. Получите выражения для погонного активного сопротивления  и погонной внутренней индуктивности провода
и погонной внутренней индуктивности провода  . Частота колебаний ω и удельная проводимость провода σ таковы, что толщина скин-слоя d «D (сильный скин-эффект).
. Частота колебаний ω и удельная проводимость провода σ таковы, что толщина скин-слоя d «D (сильный скин-эффект).
5.2.19*. Определите погонное активное сопротивление и погонную внутреннюю индуктивность медного провода диаметром 2 мм на частоте 400 МГц.
5.2.20*. Определите отношение средней плотности энергии электрического поля к средней плотности энергий магнитного поля для электромагнитной волны, проникшей внутрь реального проводника с удельной проводимостью σ и относительной магнитной проницаемостью μ = 1. Частота колебаний ω. Вычислите это отношение для меди на частоте 10 ГГц.
5.2.21*. На поверхности проводящего тела известно распределение касательной составляющей напряженности магнитного поля  . Удельная проводимость проводника σ, абсолютная магнитная проницаемость – μа частота колебаний ω. Получите выражение для средней за период колебаний энергии магнитного поля внутри проводящего тела. Считайте, что толщина скин-слоя во много раз меньше характерных размеров тела (сильный скин-эффект).
. Удельная проводимость проводника σ, абсолютная магнитная проницаемость – μа частота колебаний ω. Получите выражение для средней за период колебаний энергии магнитного поля внутри проводящего тела. Считайте, что толщина скин-слоя во много раз меньше характерных размеров тела (сильный скин-эффект).
5.2.22*. Плоская электромагнитная волна с амплитудой электрического вектора 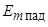 падает по нормали на плоский металлический лист, характеризующийся толщиной D, удельной проводимостью σ и относительной магнитной проницаемостью μ = 1. Лист находится в вакууме. Частота колебаний ω. Получите выражения для распределения амплитуды электрического вектора внутри листа Em(z), где z – координата изменяющаяся в направлении нормали к поверхности листа.
падает по нормали на плоский металлический лист, характеризующийся толщиной D, удельной проводимостью σ и относительной магнитной проницаемостью μ = 1. Лист находится в вакууме. Частота колебаний ω. Получите выражения для распределения амплитуды электрического вектора внутри листа Em(z), где z – координата изменяющаяся в направлении нормали к поверхности листа.
5.2.23*. В резонаторе лазера на рубине используется зеркало выполненное из металла, характеризующегося концентрацией свободных электронов Ne= 1028 м-3 и частотой соударений v = 1,5·1014 с-1. Определите коэффициент отражения по среднему значению вектора Пойнтинга при падении из воздуха на поверхность зеркала. Найдите мощность, которая будет теряться в зеркале при мощности в падающем пучке 106 Вт (используется импульсный режим генерации). Длина волны излучения воздухе λ = 0,6943 мкм.
5.2.24*. Одно из зеркал в резонаторе лазера на рубине представляет собой пластину толщиной d, выполненную из металла, характеризующегося концентрацией свободных электронов Ne= 1028 м-3 и частотой соударений v = 1,5·1014 с-1. Для передачи оптического излучения лазера из резонатора рассматриваемое зеркало должно частично пропускать излучение. Определите толщину пластины d, при которой зеркало пропускает 5% мощности. Длина волны излучения в воздухе λ = 0,6943 мкм. Считайте, что переотраженными волнами внутри пластины можно пренебречь.
5.2.25*. Плоская электромагнитная волна со средним значение вектора Пойнтинга 10 кВт/м2 падает по направлению нормали из воздуха на поверхность металла. Частота колебаний 10 ГГц. Определите удельную мощность тепловых потерь  представляющую собой среднее значение вектора Пойнтинга прошедшей волны на поверхности металла. Рассмотрите два случая: а) в металле отсутствуют сверхпроводящие электроны, удельная проводимость σ = 5,7·107 См/м; б) металл охлажден и находится сверхпроводящем состоянии, причем лондоновская длина λL = 70 нм и нормальная часть удельной проводимости σ = 2,3·10 См/м.
представляющую собой среднее значение вектора Пойнтинга прошедшей волны на поверхности металла. Рассмотрите два случая: а) в металле отсутствуют сверхпроводящие электроны, удельная проводимость σ = 5,7·107 См/м; б) металл охлажден и находится сверхпроводящем состоянии, причем лондоновская длина λL = 70 нм и нормальная часть удельной проводимости σ = 2,3·10 См/м.
5.2.26*. Плоская электромагнитная волна падает по направлени: нормали на металлическую пластинку толщиной d = 1,5 мкм. Частот колебаний 50 ГГц. Слой металла окружен воздухом. Определите затухание волны при прохождении через пластинку в двух случаях: а) в метале отсутствуют сверхпроводящие электроны, удельная проводимость σ = 1,4·10 См/м; б) металл находится в сверхпроводящем состоянии (σ = 0) и характеризуется лондоновской длиной λL = 40 нм. Считайте, что переотраженными волнами внутри пластины можно пренебречь.
5.2.27*. Плоская электромагнитная волна со средним значение вектора Пойнтинга Пср пад падает по направлению нормали на металлическую пластинку толщиной d. Металл находится в сверхпроводящем состоянии (нормальная часть удельной проводимости равна нулю) и характеризуется плазменной частотой ωпл Пластина окружена вакуумом, частота колебани ω «ωпл. Получите выражения для коэффициентов прохождения и отражени плотности потока мощности: ТП = Пср пр/Пср пад, RП = Пср отр/Пср пад, где Пср пр и Пср отр – средние значения векторов Пойнтинга для волны, прошедшей пластину и волны, отраженной от пластины, соответственно.
5.2.28*. Плоская электромагнитная волна падает по направление нормали на металлическую пластинку толщиной d = 0,1 мкм. Металл, находится в сверхпроводящем состоянии (нормальная часть удельной проводимости равна нулю и характеризуется лондоновской длиной λL = 120 нм. Пластина окружена вакуумом, длина волны в вакууме λ0 = 100 мкм. Определите, какая часть средней плотности потока мощности падающей волны проходит через пластинку. Найдите Еmпр – амплитуду напряженности электрического поля в прошедшей через слой волне, если в падающей волне Еm пад = 103 В/м.
5.2.29. Используя решения задач 5.1.54 и 5.2.27, покажите, что средняя плотность потока мощности в сверхпроводящей пластине без потерь (нормальные электроны отсутствуют) неизменна и равна средней плотности потока мощности для волны, прошедшей пластину.
5.3. Падение плоской волны на идеально проводящую плоскость
5.3.1*. Плоская электромагнитная волна с линейной поляризацией падает по нормали из воздуха на идеально проводящую плоскость. Амплитуда вектора напряженности магнитного поля падающей волны равна 0,1 А/м, частота колебаний 3 ГГц. Получите выражения, описывающие изменение амплитуды векторов Е и Н в полупространстве над границей раздела.
5.3.2*. Плоская электромагнитная волна падает по нормали из воздуха на идеально проводящую плоскость. Вектор напряженности электрического поля падающей волны на границе раздела  В/м. Получите выражения, описывающие мгновенные значения векторов Е и Н в полупространстве над проводящей плоскостью.
В/м. Получите выражения, описывающие мгновенные значения векторов Е и Н в полупространстве над проводящей плоскостью.
5.3.3. Плоская электромагнитная волна падает по нормали из воздуха на идеально проводящую плоскость. Вектор напряженности электрического поля падающей волны на границе раздела  В/м. Получите выражение, описывающее мгновенные значения вектора плотности поверхностного тока на проводящей плоскости.
В/м. Получите выражение, описывающее мгновенные значения вектора плотности поверхностного тока на проводящей плоскости.
5.3.4*. Излучение рубинового лазера с импульсной мощностью 3 кВт сформировано в виде линейно поляризованного пучка с размерам поперечного сечения 1×1 см2. Этот пучок падает по нормали из воздуха на идеально проводящую пластину и отражается от нее. Определите амплитуду тока, текущего по поверхности пластины и излучающего отраженный свет.
5.3.5. Плоская электромагнитная волна с параллельной поляризацией падает под углом 15° из вакуума на идеально проводящую плоскость. Частота колебаний 300 МГц. Определите фазовую скорость, с которой полное поле распространяется вдоль поверхности металла. Найдите минимальную высоту над границей раздела, на которой амплитуда тангенциальной составляющей вектора Н равна нулю.
5.3.6. Плоская электромагнитная волна с перпендикулярной поляризацией падает под углом 40° из вакуума на идеально проводящую плоскость. Частота колебаний 3 ГГц. Определите продольную длину волны и поперечную длину волны, характеризующие полное поле распространяющееся вдоль границы раздела.
Примечание. Продольной длиной волны называется пространственный период поля вдоль оси распространения; поперечной длиной волн называется пространственный период стоячей волны в направлении поперечном к оси распространения.
5.3.7. Решите предыдущую задачу, считая, что над идеально проводящей плоскостью находится диэлектрическое полупространство без потерь ε = 2,56; μ = 1.
5.3.8. Плоская электромагнитная волна с параллельной поляризацией падает под углом 30° из вакуума на поверхность идеального металла. Частота колебаний 20 ГГц. Определите продольную длину волны полного поля распространяющегося вдоль поверхности металла (см. примечание к задаче 5.3.6). Найдите, на какой минимальной высоте над границей раздела амплитуда касательной составляющей вектора Е будет максимальна.
5.3.9. Плоская электромагнитная волна с частотой 0,5 ГГц наклонно падает из диэлектрического полупространства без потерь с ε = 9; μ = 1 на поверхность идеального металла, при этом возникает волновой процесс распространяющийся вдоль поверхности металла с фазовой скоростью 3·108 м/с. Определите угол падения на металл исходной плоской волны.
5.3.10. Плоская электромагнитная волна с перпендикулярной поляризацией наклонно падает из вакуума на идеально проводящую плоскость. При этом над границей раздела возникает волновой процесс, распространяющийся вдоль поверхности металла (продольная длина волны равна 0,1 м) и образующий стоячую волну в направлении нормали к поверхности металла (поперечная длина волны – 0,3 м). Определите частоту колебаний поля и угол падения исходной плоской волны на проводящую плоскость.
5.3.11. Плоская электромагнитная волна с параллельной поляризацией наклонно падает из вакуума на поверхность идеального металла. Изобразите качественно зависимость амплитуды касательной составляющей магнитного вектора полного поля от координаты, изменяющейся в направлении нормали к границе раздела. На этом же рисунке покажите пунктирной линией данную зависимость для ситуации, когда угол падения исходной плоской волн увеличился в 2 раза.
5.3.12. Плоская электромагнитная волна с перпендикулярной поляризацией наклонно падает из воздуха на поверхность идеального металла. Изобразите качественно зависимость амплитуды касательной составляющей электрического вектора полного поля от координаты, изменяющейся в направлении нормали к границе раздела. На этом же рисунке покажите пунктирной линией данную зависимость для ситуации, когда над поверхностью металла находится диэлектрическое полупространство без потерь с ε = 4; μ = 1.
5.3.13. Плоская электромагнитная волна с перпендикулярной поляризацией падает под углом 35° из вакуума на идеально проводящую плоскость. Амплитуда вектора напряженности магнитного поля падающей волны 50 мА/м. Частота колебаний 10 ГГц. Определите среднее за период колебаний значение вектора Пойнтинга П ср и реактивную составляющую вектора Пойнтинга П р в полупространстве над границей раздела.
Примечание. Учтите, что 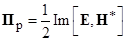 .
.
5.3.14. Плоская электромагнитная волна с параллельной поляризацией падает под углом 60° из вакуума на идеально проводящую плоскость. Амплитуда вектора напряженности электрического поля падающей волны 20 В/м. Частота колебаний 3 ГГц. Определите среднее за период колебаний значение вектора Пойнтинга П ср и реактивную составляющую вектора Пойнтинга П р в полупространстве над границей раздела (см. примечание к предыдущей задаче).
5.3.15. Плоская электромагнитная волна с параллельной поляризацией наклонно падает под углом 30° из вакуума на идеально проводящую плоскость, описываемую уравнением z = 0. Комплексная амплитуда вектор напряженности электрического поля падающей волны в точке x = y = z = 0 равна 5 В/м. Частота колебаний 300 МГц. Определите комплексную амплитуду вектора плотности поверхностного тока на проводящей плоскости.
5.3.16. Решите предыдущую задачу, считая, что падающая волна имеет перпендикулярную поляризацию.
5.3.17*. Плоская электромагнитная волна с частотой 0,9 ГГц наклонно падает из вакуума на идеально проводящую плоскость, описываемую уравнением z = 0. Комплексная амплитуда плотности поверхностного тока, протекающего по проводящей плоскости,  А/м. Определите угол падения, поляризацию и амплитуду электрического вектора падающей волны.
А/м. Определите угол падения, поляризацию и амплитуду электрического вектора падающей волны.
5.3.18. Плоская электромагнитная волна с перпендикулярной поляризацией падает под углом 55° из вакуума на идеально проводящую плоскость. Частота колебаний 2 ГГц. Определите, на каком минимальном расстоянии от границы раздела вектор напряженности магнитного поля будет иметь круговую поляризацию.
5.3.19*. Плоская электромагнитная волна с параллельной поляризацией падает под углом 20° из вакуума на идеально проводящую плоскость. Частота колебаний 0,2 ГГц. Определите ориентацию и коэффициент эллиптичности для эллипса поляризации вектора напряженности полного электрического поля на высоте 20 см над границей раздела.
5.3.20. Плоская электромагнитная волна с параллельной поляризацией падает под углом 70° из вакуума на поверхность идеального металла. При этом над границей раздела возникает волновой процесс, представляющий собой суперпозицию падающей и отраженной волн. Определите, на каком расстоянии от проводящей плоскости можно поставить вторую проводящую плоскость, если исходить из условия, чтобы вторая плоскость не возмущал волновой процесс, т.е. чтобы граничные условия на второй плоскости выполнялись автоматически – в рамках структуры поля исследуемого волнового процесса. Частота колебаний 15 ГГц. Как изменится ответ в случае, когда падающая волна имеет перпендикулярную поляризацию?





 падает по нормали из воздуха на границу раздела с металлом, характеризующимся удельной проводимостью σ и относительной магнитной проницаемостью μ = 1. Частота колебаний ω. Получите выражение для амплитуды магнитного вектора на поверхности металла
падает по нормали из воздуха на границу раздела с металлом, характеризующимся удельной проводимостью σ и относительной магнитной проницаемостью μ = 1. Частота колебаний ω. Получите выражение для амплитуды магнитного вектора на поверхности металла  . Найдите отношение
. Найдите отношение  для частоты 3 ГГц и удельной проводимости 5,7·10 См/м (медь).
для частоты 3 ГГц и удельной проводимости 5,7·10 См/м (медь).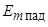 падает по нормали из воздуха на границу раздела с металлом, характеризующимся удельной проводимостью σ и относительной магнитной проницаемостью μ = 1. Частота колебаний ω. Получите выражение для амплитуды электрического вектора на поверхности металла
падает по нормали из воздуха на границу раздела с металлом, характеризующимся удельной проводимостью σ и относительной магнитной проницаемостью μ = 1. Частота колебаний ω. Получите выражение для амплитуды электрического вектора на поверхности металла  двумя способами: а) пользуясь граничными условиями Леонтовича; б) пользуясь приближенным выражением для коэффициента отражения при нормальном падении на реальный металл (задача 5.2.2.). Найдите отношение
двумя способами: а) пользуясь граничными условиями Леонтовича; б) пользуясь приближенным выражением для коэффициента отражения при нормальном падении на реальный металл (задача 5.2.2.). Найдите отношение  для частоты 1,5 ГГц и удельной проводимости 3·10 См/м.
для частоты 1,5 ГГц и удельной проводимости 3·10 См/м. ,
, 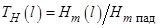 (здесь E(l) и H(l) – амплитуды электрического и магнитного векторов на расстоянии l от границы раздела).
(здесь E(l) и H(l) – амплитуды электрического и магнитного векторов на расстоянии l от границы раздела). . Получите выражение для мощности потерь, приходящейся на 1 м2 поверхности металла двумя способами: а) определив плотность потока мощности волны, проникнувшей в металл; б) воспользовавшись объемной плотностью мощности тепловых потерь внутри металла.
. Получите выражение для мощности потерь, приходящейся на 1 м2 поверхности металла двумя способами: а) определив плотность потока мощности волны, проникнувшей в металл; б) воспользовавшись объемной плотностью мощности тепловых потерь внутри металла. протекают в достаточно тонком слое у поверхности реального проводника с удельной проводимостью σ и абсолютной магнитной проницаемостью μа. При этом для определения касательной к поверхности проводника составляющей магнитного вектора
протекают в достаточно тонком слое у поверхности реального проводника с удельной проводимостью σ и абсолютной магнитной проницаемостью μа. При этом для определения касательной к поверхности проводника составляющей магнитного вектора 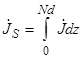 , где
, где 
 толщина скин-слоя. Покажите, что
толщина скин-слоя. Покажите, что  . Получите выражение, связывающее
. Получите выражение, связывающее 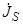 с комплексной амплитудой касательной составляющей электрического поля поверхности металла
с комплексной амплитудой касательной составляющей электрического поля поверхности металла 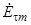 .
. . По определению, погонным внутренним импедансом провода называется отношение касательной составляющей электрического вектора на поверхности провода к полному току:
. По определению, погонным внутренним импедансом провода называется отношение касательной составляющей электрического вектора на поверхности провода к полному току:  . Получите выражения для погонного активного сопротивления
. Получите выражения для погонного активного сопротивления  и погонной внутренней индуктивности провода
и погонной внутренней индуктивности провода  . Частота колебаний ω и удельная проводимость провода σ таковы, что толщина скин-слоя d «D (сильный скин-эффект).
. Частота колебаний ω и удельная проводимость провода σ таковы, что толщина скин-слоя d «D (сильный скин-эффект). представляющую собой среднее значение вектора Пойнтинга прошедшей волны на поверхности металла. Рассмотрите два случая: а) в металле отсутствуют сверхпроводящие электроны, удельная проводимость σ = 5,7·107 См/м; б) металл охлажден и находится сверхпроводящем состоянии, причем лондоновская длина λL = 70 нм и нормальная часть удельной проводимости σ = 2,3·10 См/м.
представляющую собой среднее значение вектора Пойнтинга прошедшей волны на поверхности металла. Рассмотрите два случая: а) в металле отсутствуют сверхпроводящие электроны, удельная проводимость σ = 5,7·107 См/м; б) металл охлажден и находится сверхпроводящем состоянии, причем лондоновская длина λL = 70 нм и нормальная часть удельной проводимости σ = 2,3·10 См/м. В/м. Получите выражения, описывающие мгновенные значения векторов Е и Н в полупространстве над проводящей плоскостью.
В/м. Получите выражения, описывающие мгновенные значения векторов Е и Н в полупространстве над проводящей плоскостью. В/м. Получите выражение, описывающее мгновенные значения вектора плотности поверхностного тока на проводящей плоскости.
В/м. Получите выражение, описывающее мгновенные значения вектора плотности поверхностного тока на проводящей плоскости.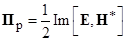 .
. А/м. Определите угол падения, поляризацию и амплитуду электрического вектора падающей волны.
А/м. Определите угол падения, поляризацию и амплитуду электрического вектора падающей волны.


