Для панельных данных типична ситуация, когда число объектов  достаточно велико. Поэтому, применяя непосредственно метод наименьших квадратов к уравнению (1), при оценивании параметров можно столкнуться с вычислительными проблемами. Их можно преодолеть, исключая из рассмотрения индивидуальные эффекты
достаточно велико. Поэтому, применяя непосредственно метод наименьших квадратов к уравнению (1), при оценивании параметров можно столкнуться с вычислительными проблемами. Их можно преодолеть, исключая из рассмотрения индивидуальные эффекты  . При этом мы понижаем размерность задачи с
. При этом мы понижаем размерность задачи с  до
до 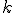 .
.
Наиболее простой способ – переход в уравнении (1) к средним по времени величинам:
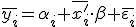 (2)
(2)
где 
Вычитая почленно (2) из (1), получаем:
 (3)
(3)
Данная модель уже не зависит от эффектов  . По существу, это уравнение (1), записанное в отклонениях от индивидуальных средних по времени.
. По существу, это уравнение (1), записанное в отклонениях от индивидуальных средних по времени.
Оценка параметров модели
Применяя обычный метод наименьших квадратов к уравнению (3), мы получим оценки
 (4)
(4)
Эти оценки называются внутригрупповыми оценками (within estimator) или оценками с фиксированным эффектом (fixed effect estimator).
Условия 1)-2), наложенные на модель, гарантируют несмещённость и состоятельность оценок с фиксированным эффектом.
В качестве оценок индивидуальных эффектов можно взять
 .
.
Эти оценки являются несмещёнными и состоятельными для фиксированного  при
при 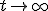
Из формулы (4) вытекает выражение для матрицы ковариации оценки  :
:
 .
.
Как и в обычной линейной модели, в качестве оценки дисперсии  можно взять сумму квадратов остатков регрессии, деленную на число степеней свободы:
можно взять сумму квадратов остатков регрессии, деленную на число степеней свободы:
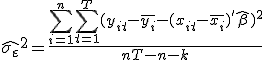 .
.
При достаточно слабых условиях регулярности оценки с фиксированным эффектом являются асимптотически нормальными (при  или при
или при  ), поэтому можно пользоваться стандартными процедурами (
), поэтому можно пользоваться стандартными процедурами (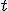 -тесты,
-тесты,  -тесты) для проверки гипотез относительно параметров
-тесты) для проверки гипотез относительно параметров  .
.
Недостатки модели панельных данных с фиксированными эффектами
В панельных данных среди независимых переменных 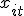 могут быть такие, которые не меняются во времени для каждого объекта. Например, при анализе заработной платы в число факторов часто включают пол или расовую принадлежность. Модель с фиксированным эффектом не позволяет идентифицировать соответствующие таким переменным коэффициенты. Формально это объясняется тем, что в уравнении (3) один или несколько регрессоров равны нулю, и, следовательно, метод наименьших квадратов применять нельзя.
могут быть такие, которые не меняются во времени для каждого объекта. Например, при анализе заработной платы в число факторов часто включают пол или расовую принадлежность. Модель с фиксированным эффектом не позволяет идентифицировать соответствующие таким переменным коэффициенты. Формально это объясняется тем, что в уравнении (3) один или несколько регрессоров равны нулю, и, следовательно, метод наименьших квадратов применять нельзя.
Модель панельных данных со случайными эффектами (random effect model) опирается на структуру панельных данных, что позволяет учитывать неизмеримые индивидуальные различия объектов. Эти отличия называются эффектами. В данной модели предполагается, что индивидуальные отличия носят случайный характер.
Описание модели панельных данных со случайными эффектами
Во введенных обозначениях модель панельных данных со случайными эффектами описывается уравнением
 (1)
(1)
где  – константа, а
– константа, а  – случайная ошибка, инвариантная по времени для каждого объекта.
– случайная ошибка, инвариантная по времени для каждого объекта.
Параметры модели: 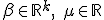 .
.
Основные предположения
Предположим, что выполнены следующие условия:
1. ошибки 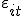 некоррелированы между собой по
некоррелированы между собой по 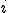 и
и 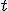 ,
,  ,
,  ;
;
2. ошибки 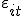 некоррелированы с регрессорами
некоррелированы с регрессорами  при всех
при всех  ;
;
3. ошибки  некоррелированы между собой по
некоррелированы между собой по 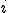 ,
,  ,
, 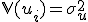 ;
;
4. ошибки  некоррелированы с регрессорами
некоррелированы с регрессорами 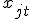 при всех
при всех  :
:  ;
;
5. ошибки  и
и 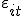 некоррелированы при всех
некоррелированы при всех  :
:  .
.
Оценка параметров модели
Модель со случайным эффектом (1) можно рассматривать как линейную модель, в которой ошибка  имеет некоторую специальную структуру. Будем рассматривать модель:
имеет некоторую специальную структуру. Будем рассматривать модель:
 (2)
(2)
Для получения оценок параметров можно применить обычный метод наименьших квадратов. Условия 1)-3) гарантируют несмещённость и состоятельность этих оценок. Однако ошибки в (2) не являются гомоскедастичными, поэтому для построения эффективных оценок можно воспользоваться обобщенным методом наименьших квадратов.





 достаточно велико. Поэтому, применяя непосредственно метод наименьших квадратов к уравнению (1), при оценивании параметров можно столкнуться с вычислительными проблемами. Их можно преодолеть, исключая из рассмотрения индивидуальные эффекты
достаточно велико. Поэтому, применяя непосредственно метод наименьших квадратов к уравнению (1), при оценивании параметров можно столкнуться с вычислительными проблемами. Их можно преодолеть, исключая из рассмотрения индивидуальные эффекты  . При этом мы понижаем размерность задачи с
. При этом мы понижаем размерность задачи с  до
до 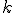 .
.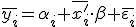 (2)
(2)
 (3)
(3) (4)
(4) .
.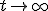
 :
: .
. можно взять сумму квадратов остатков регрессии, деленную на число степеней свободы:
можно взять сумму квадратов остатков регрессии, деленную на число степеней свободы: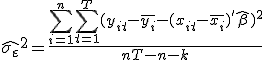 .
. или при
или при  ), поэтому можно пользоваться стандартными процедурами (
), поэтому можно пользоваться стандартными процедурами (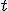 -тесты,
-тесты,  -тесты) для проверки гипотез относительно параметров
-тесты) для проверки гипотез относительно параметров  .
.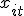 могут быть такие, которые не меняются во времени для каждого объекта. Например, при анализе заработной платы в число факторов часто включают пол или расовую принадлежность. Модель с фиксированным эффектом не позволяет идентифицировать соответствующие таким переменным коэффициенты. Формально это объясняется тем, что в уравнении (3) один или несколько регрессоров равны нулю, и, следовательно, метод наименьших квадратов применять нельзя.
могут быть такие, которые не меняются во времени для каждого объекта. Например, при анализе заработной платы в число факторов часто включают пол или расовую принадлежность. Модель с фиксированным эффектом не позволяет идентифицировать соответствующие таким переменным коэффициенты. Формально это объясняется тем, что в уравнении (3) один или несколько регрессоров равны нулю, и, следовательно, метод наименьших квадратов применять нельзя. (1)
(1) – константа, а
– константа, а  – случайная ошибка, инвариантная по времени для каждого объекта.
– случайная ошибка, инвариантная по времени для каждого объекта.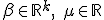 .
.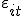 некоррелированы между собой по
некоррелированы между собой по 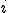 и
и  ,
,  ;
; при всех
при всех  ;
; ,
, 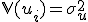 ;
;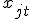 при всех
при всех  :
:  ;
; .
. имеет некоторую специальную структуру. Будем рассматривать модель:
имеет некоторую специальную структуру. Будем рассматривать модель: (2)
(2)


