Установка цветов графиков производится введением символа-обозначения цвета в число параметров функции. Обозначения цветов графиков приведены в табл. 7
Таблица 7
Обозначения цветов графиков
| Цвет
| Обозначение
цвета
|
| по-английски
| по-русски
|
| yellow
| желтый
| Y
|
| magenta
| светло-фиолетовый
| M
|
| cyan
| светло-зеленый
| C
|
| red
| красный
| R
|
| green
| зеленый
| G
|
| blue
| голубой
| B
|
| white
| белый
| W
|
| black
| черный
| K
|
Аналогично производится выбор символов для изображения графиков из таблицы 8
Таблица 8
Символы для изображения графиков
| Символ
| Обозначение
символа
|
| по-английски
| по-русски
|
| point
| точка
| .
|
| circle
| окружность
| O
|
| x-mark
| крестик
| X
|
| star
| звездочка
| *
|
| suare
| квадратик
| S
|
| diamond
| алмаз
| D
|
| triangle(down)
| треугольник(углом вниз)
| V
|
| triangle(up)
| треугольник(углом вверх)
| ^
|
| triangle(left)
| треугольник(углом влево)
| <
|
| triangle(right)
| треугольник(углом вправо)
| >
|
| pentagram
| 5-угольная звездочка
| P
|
| hexagram
| 6-угольная звездочка
| H
|
| solid
| непрерывная линия
| -
|
| dotted
| пунктирная линия
| :
|
| dashdot
| штрих-пунктирная линия
| -.
|
| dashed
| разрывная линия
| --
|
Функция hist – построение графика гистограммы заданного вектора. Стандартное обращение имеет вид: hist ( y , x ), где y – вектор, гистограмму которого нужно построить; x – вектор, определяющий интервалы изменения первого вектора, внутри которых подсчитывается число элементов вектораy.
Действия с графическими окнами. Команды работы с графическим окном находятся в главном меню окна и во всплывающем меню (щелчок правой кнопкой мыши в координатной плоскости, рис. 6).
Рис. 6. Основное меню графического окна
С его помощью могут быть выполнены различные действия с графическими окнами:
– нанесение координатной сетки (пункт всплывающего меню Grid, рис. 7);
Рис. 7. Нанесение координатной сетки
– вывод информации об отдельных точках графика (наведение курсора мыши на данную точку и нажатие левой кнопки (не отпуская)); например, для временного графика будет выведена информация о текущем значении сигнала и о текущем времени (рис. 8).
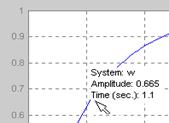
Рис. 8. Информация о координатах точки графика
Информационная надпись не исчезает при отпускании кнопки мыши. Для ее удаления необходимо щелкнуть левой кнопкой мыши на свободном поле либо правой кнопкой мыши вызвать всплывающее меню, показанное на рис. 9 и воспользоваться пунктом Delete. Аналогично выводится информационная надпись о текущем значении и текущей частоте для частотных характеристик.
Рис. 9. Всплывающее меню при работе с графиком
Масштабирование и удаление графиков. Существует несколько способов изменения масштаба графика (как временной, так и частотной характеристики).
Первый способ – использование подменю Zoom всплывающего меню (см. рис. 6). Пунктами подменю Zoom являются:
In - X – масштабирование по горизонтали;
In - Y – масштабирование по вертикали;
X - Y – масштабирование по вертикали и по горизонтали (выделение прямоугольного фрагмента);
Out – возврат исходного масштаба.
Масштабирование выполняется мышью, при удержании нажатой левой кнопки, путем проведения горизонтальной линии (In - X), вертикальной линии (In - Y) или прямоугольника (X - Y).
Второй способ изменения масштаба – использование окна параметров координатной плоскости. Для вывода окна параметров необходимо сначала войти в режим редактирования графического окна, нажав мышью кнопку с изображением стрелки в меню окна, а затем выполнить двойной щелчок по координатной плоскости (но не по самому графику!). В результате появится окно параметров (рис. 10).
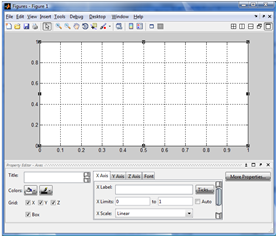
Рис. 10. Окно параметров графического окна
Максимальное и минимальное значения по оси X и оси Y (для разных характеристик эти оси имеют разный смысл) задаются в строках ввода напротив надписи Limits. При этом должен быть установлен флажок ручного ввода пределов Manual.
Иногда требуется скрыть некоторые графики (если на одной координатной плоскости их несколько). Для того чтобы скрыть графики (с возможностью последующего восстановления) используется всплывающее меню графического окна (режим редактирования выключен). В подменю Systems перечислены имена всех объектов, характеристики которых были выведены в окно. Для того чтобы скрыть график, необходимо снять флажок напротив имени объекта.
Изменение параметров графиков. Для изменения параметров графика можно использовать всплывающее меню графика (рис. 10). Для его вывода необходимо в режиме редактирования графического о кна выполнить щелчок правой кнопкой мыши при наведении курсора на сам график.
Для изменения толщины линии используется подменю Line Width, для изменения стиля линии (сплошная, пунктирная и т.д.) – подменю Line Style. При выборе пункта Color … появляется окно установки цвета линии. Те же действия можно выполнить, используя окно установки параметров графика (пункт Properties …).
Оформление графического окна. Для добавления текстовых комментариев нажмите мышью кнопку Insert – TextBox меню графического окна. Затем выполните щелчок мыши в нужном месте координатной плоскости, введите текст и выполните щелчок мыши в любом другом месте координатной плоскости. В режиме редактирования графического окна можно перетаскивать текстовую надпись с помощью мыши на любое место координатной плоскости.
Для введения заголовка над координатной плоскостью заполните строку Title в окне параметров Insert. Для введения поясняющих надписей для осей – строки Label для оси X и для оси Y.
Сохранение графического окна. Для сохранения координатной плоскости и ее содержимого в графическом файле используется пункт Export … в подменю File … главного меню графического окна. В окне сохранения файла задается тип файла (например, Bitmapfiles *. bmp) и имя файла. Файлы типа Bitmap могут быть открыты графическим редактором Paint.
Ввод и действия с комплексными числами. Язык системы M atlab, в отличие от многих языков программирования высокого уровня, содержит очень простую в пользовании встроенную арифметику комплексных чисел Большинство элементарных математических функций построено таким образом, что аргументы предполагаются комплексными числами, а результаты также формируются как комплексные числа. Эта особенность языка, делает его очень полезным для инженеров и научных работников.
Для обозначения мнимой единицы в M atlab зарезервировано два имени - i и j. Ввод с клавиатуры значения комплексного числа производится путем записи в командном окне строки вида:
<Имя переменной> = <Значение ДЧ> + i*<Значение МЧ>,
где ДЧ - действительная часть комплексной величины;
МЧ - мнимая ее часть.
Пример ввода комплексного числа:
I=34.63-j*13.965
I =
34.63 - 13.965i
Простейшие действия с комплексными числами - сложение, вычитание, умножение, деление и возведение в степень - осуществляются с помощью обычных арифметических знаков +, -, *, /, \ и ^ соответственно. Далее, в разделе расчетов цепей переменного тока мы покажем, как это выглядит на примерах.
Практически все элементарные математические функции, переченькоторых приведен далее, вычисляются при комплексном значении аргумента и получают в результате этого комплексные значения результата.
Благодаря этому, например, функция sqrt (корень квадратный), в отличие от других языков программирования, вычисляет квадратный корень из отрицательного аргумента, а функция abs (абсолютное значение) при комплексном значении аргумента вычисляет модуль комплексного числа.
» x=sqrt(5-j*4)
x =
2.3878 - 0.83759i
» y=abs(x)
y =
2.5304
В M atlab есть несколько дополнительных функций, рассчитанныхтолько на комплексный аргумент:
real(Z) - выделяет действительную часть комплексного аргумента Z;
imag(Z) - выделяет мнимую часть комплексного аргумента;
angle(Z) - вычисляет значение аргумента комплексного числа Z (врадианах от -π до +π);
conj(Z) - выдает число, комплексно сопряженное относительно Z.
Кроме того, в M atlab есть специальная функция cplxpair(V), которая осуществляет сортировку заданного вектора V с комплексными элементами таким образом, что комплексно-сопряженные пары этих элементов располагаются в выходном векторе в порядке возрастания их действительных частей, при этом элемент с отрицательной мнимой частью всегдарасполагается первым. Действительные элементы завершают комплексно-сопряженные пары.
Приспособленность большинства функций M atlab к оперированию с комплексными числами позволяет значительно проще строить вычисления с действительными числами, результат которых является комплексным (например, находить комплексные корни квадратных уравнений).
Решение систем линейных уравнений в среде MatLab . Система MatLab имеет библиотеку для реализации задач линейной алгебры. В ее составе можно выделить, в частности, следующие функции и операции.
D=det(A) - определитель (для квадратной матрицы);
R=rank(A) - ранг матрицы (число линейно независимых строк / cтолбцов);
T=norm(A) - норма матрицы ||A||2;
О=inv(A) - обращение матрицы (при близости матрицы к вырожденной выдаются предупреждения о ненадежности результатов); часто используется для решения системы АХ=В в форме:
Х= inv(A) *В;
X=B/A , X=A\B - решение системы АХ=В (B –матрица правой части):
» A=[1 2; 3 1]
A=12
31
» B=[5;5]
B=5
5
» X=A\B
X=1
2
» X=B'/A'
X = 1 2
» B=[5 13;5 17]
B=5 13
5 17
» X=A\B
X=1.0 4.20
2.0 4.40
Интегрирование системы обыкновенных дифференциальных уравнений осуществляется при помощи функций ode 23 и ode 45. Функция ode 23 осуществляет интегрирование численным методом Рунге-Кутта 2-го порядка, а с помощью метода 3-го порядка контролирует относительные и абсолютные ошибки интегрирования на каждом шаге и изменяет величину шага интегрирования так, чтобы обеспечить заданные пределы ошибок интегрирования. При использовании функции ode 45 интегрирование осуществляется методом Рунге-Кутта 4-го порядка, а величина шага контролируется методом 5-го порядка.
Система дифференциальных уравнений должна быть представлена в форме Коши:
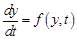 ,
,
где y – вектор переменных состояния системы, t – аргумент (обычно время), f – нелинейная вектор-функция от переменных состояния у и аргумента t.
Обращение к процедурам численного интегрирования имеет вид
[t, y] = ode23(‘< имя функции >’, tspan, y0, options)
[t, y] = ode45(‘< имя функции >’, tspan, y0, options),
где <имя функции> – имя m-файла, являющегося функцией Matlab от t и y , в котором вычисляется вектор функция f(y , t), т.е. правые части системы дифференциаль-ных уравнений; tspan – вектор задающий интервал интегрирования [t0 tfinal], t0 – начальное значение интервала, tfinal – конечное; y0 – вектор начальных условий; options – строка параметров, определяющих значения допустимой относительной и абсолютной погрешности интегрирования. Этот параметр можно не указывать, если пользователя устраивают значения погрешностей, заданных по умолчанию, т.е. относительная погрешность интегриро-вания 1.0e-3,а абсолютная (по каждой из переменных состояния) – 1.0e-6. В противном случае, перед обращением к процедуре ode 23 следует указать значения погрешностей при помощи процедуры odeset.
Результатом интегрирования является матрица проинтегрированных значений фазовых переменных y, в которой каждый столбец соответствует одной из переменных состояния, а строка содержит значения переменных состояния, соответствующих определенному шагу интегрирования, т.е. значению вектора t.
Пусть задана система обыкновенных дифференциальных уравнений:
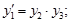
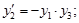
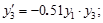
с начальными условиями: 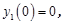
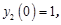
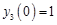 .
.
Для интегрирования данной системы уравнений необходимо создать m-файл, который является функцией переменных t и y. Для создания файла воспользуемся редактором Matlab Editor / Debugger, который вызывается из основного меню File – New – Blank M-File. Текст файла:
Function
dy=rigid(t,y)
dy=zeros(3,1);
dy(1)=y(2)*y(3);
dy (2)=- y (1)* y (3);
dy (3)=-0.51* y (1)* y (2);
Название файла и функции должны совпадать. Файл надо сохранить с названием rigid.
В этом примере абсолютная и относительная погрешность задается при помощи команды odeset, время интегрирования зададим в интервале от 0 до 12 [0 12], вектор начальных условий [0 1 1]. Для осуществления процедуры интегрирования в рабочем пространстве Matlab необходимо набрать:
» options=odeset('RelTol',1e-4,'AbsTol',[1e-4 1e-4 1e-5]);
» [t,y]=ode45('rigid',[0 12],[0 1 1],options);
Чтобы просмотреть результаты в рабочем пространстве Matlab необходимо ввести в командной строке y. Графически результаты выводятся при помощи команды plot
» plot(t,y(:,1),'-',t,y(:,2),'-.',t,y(:,3),'.').
с постоянными параметрами. Объект может являться моделью всей системы, ее части или отдельного элемента системы.
Нахождение корней полиномов. Система Matlab имеет функцию roots ( P ), которая вычисляет вектор, элементы которого являются корнями заданного полинома Р.
Рассмотрим пример. Пусть задан полином:
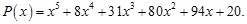
В системе Matlab полином задается вектором его коэффициентов:
>> p=[1,8,31,80,94,20].
При вводе функции roots ( p ) вычисляются корни полинома p:
>> roots ( p ).
Ввод моделей в виде пространства состояний производится по заданным матрицам A, B, C, D уравнений состояния системы:
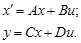
Матрицы вводятся в рабочем пространстве Matlab в квадратных скобках по срокам через точку с запятой. Например, матрица
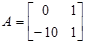
вводится следующим образом:
>> A=[0 1;−10 1].
Модель в виде пространства состояний вводится при помощи функции
sys = ss ( A , B , C , D ),
где sys – произвольное название системы. Перед вводом этой команды необходимо ввести в рабочее пространство Matlab последовательно матрицы A,B,C,D.
Построение основных характеристик объекта. Создав объект с определенной структурой и параметрами, можно исследовать различные характеристики объекта. Графики характеристик строятся в специальных графических окнах. Рассмотрим способы получения основных временных и частотных характеристик (табл.9 – 12).
Примечание 1. Обозначение координатных осей графического окна производится при выводе временных характеристик:
Amplitude – ось значений выходной величины объекта;
Time ( sec ) – ось времени (единицы – секунды).
Таблица 9
Исследование переходной функции и весовой функции
| Команда
| Комментарий
|
|
step(w)
impulse(w)
| Построение переходной функции (step) и весовой функции (impulse) функции объекта w. Время моделирования определяется автоматически
|
|
step(w,t)
impulse(w,t)
| Построение переходной (весовой) функции объекта wна заданном отрезке времени от 0 до t (где t – это константа или переменная); t также можно задавать как массив вида 0: dt : tmax, где tmax – время окончания моделирования, dt – шаг расчета переходной функции (должен быть достаточно малым)
|
| step(w1,w2,…,wn)
impulse(w1,w2,
…,wn)
| Построение переходной (весовой) функции нескольких объектов на одной координатной плоскости
|
| step(w1,w2,…,wn,t)
impulse(w1,w2,
…,wn,t)
|
То же с заданием времени моделирования
|
Таблица 10
Исследование реакции на произвольно заданное воздействие
| Команда
| Комментарий
|
|
lsim(w,u,t)
| Построение реакции объекта w на воздействие заданное двумя массивами. Массив t – это массив значений времени. Задается в виде 0: dt : tmax, где tmax – время окончания моделирования, dt – шаг расчета (должен быть достаточно малым). Массив u – это массив значений входного воздействия того же размера, что и массив t
|
| lsim(w1,w2,…,wn,u, t)
| То же для нескольких объектов (графики выводятся на одну координатную плоскость)
|
Таблица 11
Исследование АФЧХ – амплитудно-фазовой частотной характеристики (Nyquistdiagram)
| Команда
| Комментарий
|
| nyquist(w)
| Построение АФЧХ объекта w
|
|
nyquist(w,{omin,omax})
| То же с заданием диапазона частот, для которого строится АФЧХ (в фигурных скобках). Частота ominдолжна быть больше нуля
|
| nyquist(w1,w2,…,wn)
| Построение АФЧХ нескольких объектов на одной комплексной плоскости.
|
| nyquist(w1,
…,wn,{omin, omax})
| То же с заданием диапазона частот
|
Примечание 2. Амплитудно-фазовая частотная характеристика строится в виде годографа на комплексной плоскости для диапазона частот –∞…∞ и представляет собой две симметричные относительно действительной оси кривые: одна для положительных частот, другая для отрицательных частот. В отечественной литературе принято строить амплитудно-фазовую частотную характеристику строить только для положительных частот. Обозначение осей комплексной плоскости в графическом окне: RealAxis– действительная ось, ImaginaryAxis – мнимая ось.
Таблица 12
Исследование ЛЧХ – логарифмических частотных характеристик
(Bodediagram)
| Команда
| Комментарий
|
| bode(w)
| Построение ЛЧХ объекта w
|
| bode(w,{omin, omax})
| То же с заданием диапазона частот
Частота omin должна быть больше нуля
|
| bode(w1,w2,…,wn)
| Построение ЛЧХ нескольких объектов в одном окне
|
| bode(w1,w2,…,wn,{omin, omax})
| То же с заданием диапазона частот
|
|
margin(w)
| Построение ЛЧХ объекта w с выводом информации о запасах устойчивости автоматической системы по амплитуде и по фазе. Объект w должен описывать разомкнутую систему
|
Примечание 3. Команды bode и margin всегда строят 2 логарифмические частотные характеристики в одном окне друг под другом в одном масштабе частоты: ЛАЧХ – логарифмическую амплитудную частотную характеристику и ЛФЧХ – логарифмическую фазовую частотную характеристику. Обозначение координатных осей: Magnitude(dB) – ось значений амплитудно-фазовой частотной характеристики в децибелах, Phase(deg) – ось значений логарифмической фазовой частотной характеристики в градусах, Frequency(rad / sec) – ось частоты (в радианах в секунду).
Для того чтобы построить новую характеристику в другом графическом окне (при сохранении на экране уже имеющегося графического окна) необходимо ввести команду figure (создается новое пустое графическое окно); после запуска следующей команды вывода графиков они появятся в новом окне. При построении нескольких характеристик на одной координатной плоскости каждый график строится своим цветом в зависимости от порядка построения. Стандартным для Matlab является следующий порядок цветов графиков: синий, зеленый, красный, голубой, фиолетовый.
Построение амплитудно-фазовой характеристики W(jw) в командном окне Matlab. Набор исходных данных, функции W и графической команды plot представлен ниже:
>> k=12;
z=0.1;
T=1;
w=0:0.01:100;
W=k./(T.^2.*(w.*j).^2+2.*T.*z.*w.*j+1);
Plot(real(W), imag(W))
Далее с помощью пункта меню Insert → XLabel → LabelY → Title окна Figure № вводятся обозначения осей и заголовок рисунка. Общий вид изображения амплитудно-фазовой характеристики показан на рис. 18.
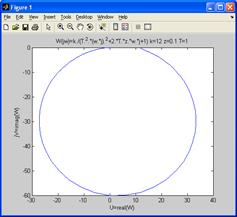
Рис. 18. Изображение амплитудно-фазовой характеристики
Щелкнув правой кнопкой мыши на поле рисунка, можно вызвать всплывающее меню, с помощью которого вводится координатная сетка (пункт Grid). С помощью пункта меню View → Plot Browser можно изменить тип, форму и цвет линий графика.
Построение расчетных логарифмических амплитудной LР (w) и фазовой arР(w) частотных характеристик производится в соответствии со следующими ниже правилами.
1. Характеристики строятся в полулогарифмических координатах (ось Х – логарифмическая, ось У – естественная) с использованием функции semilogx, у которой правила ввода аргументов и значений спецификатора кривой аналогичны функции plot.
2. В силу особенностей функции Matlab atan(x) = arctg(x) (выдаются значения только в диапазоне от -π/2 до π/2), функция ar(w) набирается в виде двух выражений (см. текст последовательности вычислений ниже).
3. Каждая характеристика набирается отдельным графиком, и ввод заканчивается командой holdon, обеспечивающей вывод последующего графика в то же текущее окно рисунка.
4. Из набранных осевых надписей Matlab выводит только последние (ar2 и log(w2)).
Для вывода всех необходимых надписей следует:
– в окне Figure No.1 командой меню Edit – AxesProperties вызвать окно редактора заголовка и осевых надписей (Property Editor) и ввести необходимые тексты; кнопки Editрядом с каждым оконцем позволяют менять у текста тип шрифта и его параметры;
– нажатием кнопки «А» и щелчком левой кнопки мышки ввести текстовое поле (с последующим вводом текста) для пометки выбранной кривой (стрелка вставляется нажатие кнопки «Стрелка» с последующим вычерчиванием линии левой кнопкой мышки).
Характеристики набираются в командном окне согласно формул (10) и (11) в соответствии с цепочкой команд:
>> k=12;
z=0.1;
T=1;
w=0:0.01:100;
W=k./(T.^2.*(w.*j).^2+2.*T.*z.*w.*j+1);
L=20.*log10(k./sqrt((2.*T.*z.*w).^2+(1-T.^2.*w.^2).^2));
semilogx(w,L);
hold on;
w1=0.1:0.01:1;
ar1=-(180./pi).*atan(2.*T.*z.*w1./(1-T.^2.*w1.^2));
semilogx(w1,ar1);
hold on;
w2=1.01:0.01:100;
ar2=-180-(180./pi).*atan(2.*T.*z.*w2./(1-T.^2.*w2.^2));
semilogx(w2,ar2);
Warning: Divide by zero.
(Type "warning off MATLAB:divideByZero" to suppress this warning.).
После нажатия клавиши Enter , завершающего ввод команд, Matlab построит графики на поле рисунка FigureNo .1 (рис.19), причем надписи на рисунке дополнительно редактируются средствами окна рисунка Figure No .1.
Последние две строки – это сообщение Matlab, которое игнорируется.
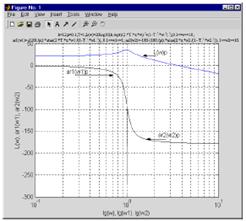
Рис.19. Логарифмические амплитудная и фазовая частотные характеристики звена
Работа с приложением Simulink
Модели элементов. После запуска Matlab запуск Simulink может быть произведен с использованием соответствующего раздела меню Start пакета Matlab (рис. 20).
При этом происходит переход к обозревателю библиотеки модулей Simulink Library Browser, из которой вызываются модели компонентов исследуемой системы, показанные на рис. 21.
В настоящей работе мы будем пользоваться частью библиотеки Simulink, включающей в себя разделы:
– Continuous – модели линейных непрерывных систем;
– Math Operations – модели математических операций;
– Sinks – приемники сигналов;
– Sourses – источники сигналов;
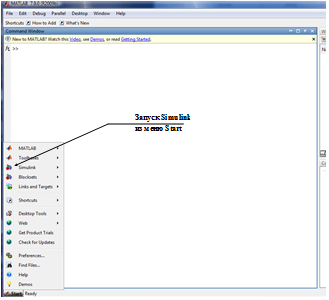
Рис. 20. Средства запуска Simulink
Приложение SimPowerSystem, непосредственно используемое для решения задач электротехники, рассматривается в следующих лабораторных работах.
Библиотека блоков. Внешний вид наиболее часто встречающихся в системах управления элементов показан на рис. 22.
Рассмотрим некоторые блоки, входящие в состав библиотеки. Каждый блок имеет определенное число входов и выходов для связи с другими блоками модели. Некоторые блоки имеют только входы или только выходы. Свойства блоков определяются параметрами, задаваемыми пользователем. Эти параметры вводятся в окне параметров, для раскрытия которого выполняется двойной щелчок левой кнопкой мыши по изображению блока.
Первые четыре блока (рис.22, а–г, библиотека Sourses)
представляют собой настраиваемые источники сигнала. Они имеют один выход и не имеют входов.
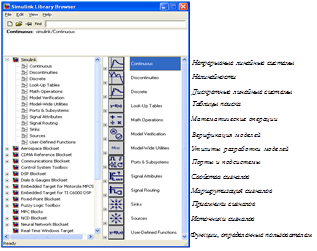
Рис. 21. Окно библиотеки модулей Simulink

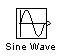
а б в г

д е ж з
и к
Рис. 22. Блоки-компоненты систем управления
Источник постоянного сигнала (константа), рис.22, а, формирует постоянный сигнал заданной величины.
Параметр блока: ConstantValue – значение константы.
Источник ступенчатого сигнала (Step), рис.22,б, формирует ступенчатый сигнал (рис. 23).
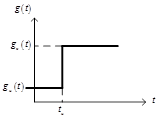
Рис. 23. Ступенчатый сигнал
Параметры блока:
Steptime – время скачка сигнала.
Initialvalue – начальное значение.
Finalvalue – конечное значение.
Источник линейно изменяющегося сигнала (Ramp), рис. 22,в, формирует сигнал, возрастающий или убывающий с постоянной скоростью (рис. 24).

Рис. 24. Линейно возрастающий сигнал
Параметры блока:
Slope – наклон (значение производной по времени).
Starttime – время начала действия сигнала.
Источник синусоидального сигнала, рис. 22,г, формирует сину-соидальный сигнал с заданной частотой, амплитудой и начальной фазой.
Параметры блока:
Amplitude – амплитуда.
Frequency ( rad / sec ) – частота в рад/с.
Phase ( rad ) – начальная фаза в радианах.
Графический индикатор сигналов, рис.22,д, предназначен для наблюдения результатов моделирования – временных графиков величин модели. Блок имеет один вход, куда подается исследуемый сигнал модели, и не имеет выходов. В модели можно использовать только один индикатор. Наблюдение нескольких графиков в одном окне осуществляется с помощью мультиплексора. После того как расчет модели произведен компьютером, можно посмотреть результат, для чего необходимо выполнить двойной щелчок по значку индикатора. В результате раскрывается графическое окно с графиком сигнала в функции времени.
Мультиплексор, рис.22,е, имеет несколько входов, число ко-торых определяется пользователем, и один выход. Мультиплексор объединяет несколько сигналов в один векторный сигнал, который передается в модели по одной линии. Использование мультиплексора позволяет подать на индикатор несколько сигналов и наблюдать их графики на одной координатной плоскости.
Параметр блока: Number of inputs – число входов.
Остальные блоки (рис. 22,ж – к) представляют собой преобразователи сигналов.
Линейное динамическое звено, рис. 22, ж.
Параметры блока:
Numerator – массив коэффициентов числителя передаточной функции.
Denominator – массив коэффициентов знаменателя передаточной функции.
Коэффициенты числителя и знаменателя передаточной функции задаются по тем же правилам, как в Control System Toolbox. После ввода параметров передаточная функция показывается внутри значка блока.
Пропорциональное звено, рис. 22, з, умножает сигнал на величину Gain.
Параметр блока: Gain – коэффициент передачи.
Звено запаздывания, рис. 22, и, выполняет задержку сигнала на выходе блока относительно входного сигнала, при этом полностью сохраняет форму входного сигнала.
Параметр блока: Time delay – время задержки.
Сумматор, рис. 22, к, выполняет алгебраическое суммирование (сложение или вычитание) заданного числа входных сигналов. Графическая форма сумматора может быть изменена после вывода элемента в окно модели (щелчок на сумматоре левой кнопкой мыши →Sum parameters во всплывающем окне →Icon Shape).
Параметр блока: List of signs – список знаков. В список знаков записываются плюсы и минусы без пробелов (например +–++). Тем самым определяется число входов сумматора, и знак каждого слагаемого.
Действия с блоками. В состав основных действий с блоками входят:
– вставка блока из библиотеки в окно модели;
– выделение блока;
– удаление блока;
– изменение размеров блока;
– изменение атрибутов блока;
– копирование блока;
– изменение ориентации блока.
Вставка блока из окна библиотеки в окно модели выполняется с помощью мыши (удерживая левую кнопку). При этом окно модели должно быть предварительно создано (File → New → Model).
Выделение блоков. Блок может быть выделенным или невыделенным. Для выделения блока выполняется однократный щелчок левой кнопкой мыши по значку блока. Выделение показывается четырьмя квадратными метками по углам значка блока (рис. 25, а). Для выделения нескольких блоков выполняется однократный щелчок мышью по значкам блоков с удержанием клавиши Shift или путем обведения прямоугольного участка окна рамкой.
Удаление блоков. Нажатие клавиши Delete приводит к удалению всех выделенных блоков.
а б в
Соединение выполнено Соединение не выполнено
г д
Рис. 25. Действия с блоками
Изменение размеров блока. Значок блока можно растягивать, захватив мышью за квадратные угловые метки.
Изменение имени блока. Чтобы ввести новое имя блока выполняется однократный щелчок левой кнопкой мыши по старому имени. Имя блока обводится рамкой и появляется курсор (рис. 25,б). После этого можно редактировать имя. Не допускается отсутствие имени блока (пустая строка) и наличие в одном окне блоков с одинаковыми именами.
Вращение блока. При выполнении щелчка правой кнопкой мыши по значку блока появляется всплывающее меню блока, где находится подменю Format. В подменю Format содержатся команды: Rotate block – вращение блока на 90° по часовой стрелке, Flip block – разворот блока на 180°, Flip name – переброска имени на другую сторону блока.
Создание копии блока. Для создания копии необходимо захватить блок, удерживая правую кнопку мыши и перетащить на свободное место окна.
Сборка схемы модели. Сборка модели включает в себя выполнение следующих действий:
– компоновка блоков;
– проведение и корректировка соединительных линий;
Компоновка блоков состоит в таком их размещении на экране, при котором структура соединительных линий будет выглядеть наиболее просто.
Проведение соединительных линий. Для соединения выхода одного блока с входом другого указатель мыши наводится на исходную точку и затем проводится линия (удерживая левую кнопку мыши). Когда линия доведена до конечной точки, кнопка мыши отпускается. Жирный конец стрелки означает, что соединение выполнено (рис.25, г). Если линия осталась не подключенной, конец стрелки будет тонким (рис.25, д). Неподключенную стрелку затем можно продолжить. Линии можно захватывать мышью и изменять их конфигурацию.
Отделение блока от линии. Для отделения блока он захватывается мышью с удержанием клавиши Shift и перетаскивается на другое место.
Удаление линий. Линии, как и сами блоки, можно выделять. После нажатия клавиши Delete выделенные линии удаляются.
Создание узлов. Для создания узла на линии новая линия тянется от выбранной точки с удержанием правой кнопки мыши (рис.10, в).
Чтобы собрать схему, сначала необходимо выполнить следующие действия:
1. "Перетащить" все нужные звенья из соответствующих наборов на пространство модели untitled, предназначенное для составления блок-схемы вашей модели. Делается это следующим образом: выбрать элемент в библиотеке, нажать на элементе левой кнопкой мыши и, не отпуская кнопку, перенести указатель мыши в окно построения модели и там отпустить.
В соответствии со схемой на рис. 4 нам необходимы: источник скачкообразного возмущения для 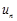 , сумматор, три усилителя, два интегратора, два источника постоянного сигнала (для задания начальных условий) и осциллограф. После выбора на структурной схеме модели будут помещены все необходимые элементы, рис. 26.
, сумматор, три усилителя, два интегратора, два источника постоянного сигнала (для задания начальных условий) и осциллограф. После выбора на структурной схеме модели будут помещены все необходимые элементы, рис. 26.
2. Связать между собой эти звенья, соединив их в соответствии со схемой, рис. 4. Для этого вначале необходимо разместить звенья так, чтобы было удобно проводить соединения. Затем нужно установить курсор на выходе нужного звена и нажать левую кнопку мыши. При этом указатель примет вид перекрестия. Теперь, не отпуская кнопки, "тащить" появившуюся линию до входа другого звена. Когда указатель примет вид двойного перекрестия, отпустить кнопку. Система создаст связь между элементами и обозначит ее стрелкой по направлению сигнала.
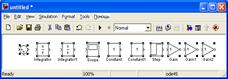
Рис. 26. Пространство модели с размещенными в не










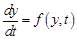 ,
,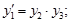
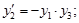
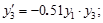
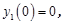
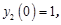
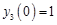 .
.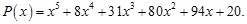
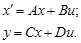
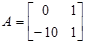




















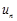 , сумматор, три усилителя, два интегратора, два источника постоянного сигнала (для задания начальных условий) и осциллограф. После выбора на структурной схеме модели будут помещены все необходимые элементы, рис. 26.
, сумматор, три усилителя, два интегратора, два источника постоянного сигнала (для задания начальных условий) и осциллограф. После выбора на структурной схеме модели будут помещены все необходимые элементы, рис. 26.


