Рис. 2. Правильная запись вычисления функции на одномерном (а) и
многомерном (б) массивах и неправильная (в) (пропуск точки с запятой после первого оператора)
12. Если не указана переменная для значения результата вычислений, то Matlab назначает такую переменную с именем ans.
13. Результат вычислений выводится в строках вывода (без знака >>).
14. Для вычисления функции на одномерном или многомерном матричных массивах значений аргумента необходимо выполнить действия согласно рис.13.
В векторе (одномерном массиве) значения заключены в квадратные скобки и отделяются друг от друга пробелом (рис.3, а); в матрице (многомерном массиве) значения заключены тоже в квадратные скобки, причем, строки отделяются точкой с запятой (порядок следования строк: левая выше правой), а значения в каждой строке отделяются аналогично вектору (рис.3, б).
15. Если значения аргумента вычисляемой функции являются членами отрезка арифметической прогрессии с заданной разностью (шагом), то для записи аргумента применяется оператор «:» (двоеточие), как показано на рис. 3. При разности, равной единице, ее запись в операторе можно опускать (рис. 3, б).
а) » x=[1:2.5:16.5];
Y=sin(x)
Y =
0.8415 –0.3508 –0.2794 0.7985 –1.0000 0.8038 –0.2879
б) » x=1:10;
Y=sin(x)
Y = Columns 1 through 7
0.8415 0.9093 0.1411 –0.7568 –0.9589 –0.2794 0.6570
Columns 8 through 10
0.9894 0.4121 –0.5440
в) x =[1:2.5:11.5; 2:6];
Y = sin ( x )
Y = 0.8415 -0.3508 -0.2794 0.7985 -1.0000 0.9093 0.1411 -0.7568 -0.9589 -0.2794
Рис. 3. Правильная запись вычисления функции на одномерном массиве аргумента в виде отрезка арифметической прогрессии (с разностями 2,5 (а) и 1 (б)) и в виде 2-строчной матрицы с теми же разностями (в)
Для правильной записи значений матрицы аргумента, когда ее строки являются отрезками арифметических прогрессий, необходимо руководствоваться правилами 14 и 15 одновременно.
16. Комментарии записываются в отдельную строку, помечаемую знаком «%» (процент) в первом знакоместе строки (см. рис. 4, а).
Разбиение строки с длинным выражением или комментарием на две производится установкой курсора перед переносимой на создаваемую вторую строку частью выражения и нажатием клавиш Shift + Enter (рис. 4, б) – двукратное разбиение выражения х = [23 45 67 45] на три строки).
17. Соединение двух строк в одну в программе или в выражении производится установкой курсора в начало второй строки и нажатием клавиш Shift + Backspace. Эта операция над строками с выражениями 67 и 45 показана рис. 4, в.
а)»x=[0.5 0.7 1];
Y=sin(x)
% Комментарии размещаются в отдельных строках
Y =
0.4794 0.6442 0.8415
б)» x=[23 45 67 45]
x=[23 45
67
45]
в)» x=[23 45 67
45]
Рис. 4. Ввод комментария в вычисляемое выражение или программу (а), разбиение первой строки на три (б), объединение 3-й и 2-й строк (в)
18. Вычисляемое выражение сразу после завершения вычисления можно ввести вновь в текущее место ввода нажатием кнопки «стрелка вверх» ↑(для изменения величин аргументов или коррекции выражения).
Повторное нажатие кнопки ↑ заменит текущие условия на условия, им предшествующие: этот процесс можно повторять многократно, добиваясь вызова в место ввода все более ранних вычислительных условий.
Ранее вытеснявшееся выражение можно быстро вставить в место ввода путем выделения его левой кнопкой мышки (кнопка далее отпускается) и небольшого протягивания его вниз повторно нажатой левой кнопкой: Matlab сам вставит выделенное выражение.
19. Ранее примененную функцию можно вставить в командное окно через копирование её из окна Command History (Протокола команд), в котором все ранее использованные команды и функции сохраняются до тех пор, пока пользователь не удалит их.
20. Чтобы сохранить данные вычислений в окне управления (выражения, программы, результаты или их части) для повторного вызова и работы, необходимо:
− выделить данные,
− скопировать их в буфер,
− вызвать редактор-отладчик m-файлов через меню «Файл-Создать- m -файл», либо командой edit в командном окне,
− вставить скопированные данные в открывшийся новый m-файл и сохранить его через меню редактора File - SaveAs … («Файл-Сохранить как»).
21. Для продолжения вычислительной работы в окне управления с данными, сохраненными по правилам п.20, необходимо через меню «Файл-Открыть» открыть требуемый файл, выделить в нем требуемые для работы фрагменты, скопировать их в буфер и вставить в текущее место ввода окна управления.
Рассмотрим применение перечисленных выше правил для выполнения вычислений.
Использование переменных. Результат вычислений можно присвоить любой переменной, определенной пользователем. Имя переменной должно начинаться с буквы и может состоять из букв, цифр и символа подчеркивания. Система Matlab различает строчные и прописные буквы в именах переменных (A и a – это разные переменные). Знак = соответствует операции присваивания. Значения переменных, вычисленные в течение текущего сеанса работы, сохраняются в специально зарезервированной области памяти компьютера, называемой рабочим пространством (Workspace). Использование переменных рассмотрено в примере 1.
Пример 1. Использование переменных
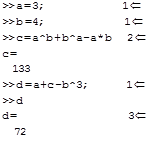
Комментарии к вычислениям:
 Если в конце строки ставится точка с запятой, то результат не будет выведен после нажатия Enter.
Если в конце строки ставится точка с запятой, то результат не будет выведен после нажатия Enter.
 Здесь нет точки с запятой, и после нажатия Enter результат выводится и присваивается переменной c.
Здесь нет точки с запятой, и после нажатия Enter результат выводится и присваивается переменной c.
 Для того чтобы узнать значение переменной достаточно ввести ее имя в командную строку и нажать Enter.
Для того чтобы узнать значение переменной достаточно ввести ее имя в командную строку и нажать Enter.
Использование Matlab как калькулятора иллюстрирует также пример 2.
Пример 2. Использование Matlab как калькулятора
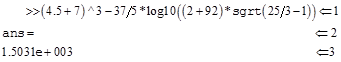
Комментарии к вычислениям:
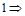 Нажатие клавиши Enter.
Нажатие клавиши Enter.
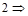 Результат присваивается переменной с именем ans
Результат присваивается переменной с именем ans
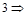 Результат выводится в формате с плавающей точкой. Такая запись означает 1,5031·103.
Результат выводится в формате с плавающей точкой. Такая запись означает 1,5031·103.
Длинные выражения можно записать в нескольких строках с использованием в качестве знака переноса символа многоточия ….
Использование массивов . В системе Matlab также используются массивы, математической формой представления которых являются матрицы. Напомним основные действия над матрицами и их реализацию в Matlab.
1. Присвоение значений матрице. Простейшей операцией с матрицей является ее создание. Для создания столбца необходимо указать его имя, знак равенства и в квадратных скобках через запятую или через пробел перечислить значения элементов. Например:
A=[1 2 3 4 5]
A =
1 2 3 4 5
В случае, если необходимо создать столбец чисел, то в качестве разделителя используется символ «;» (точка с запятой), например:
A =[1;2;3;4;5]
A =
1
2
3
4
5
Для создания квадратной или прямоугольной матрицы необходимо чередовать оба этих способа, например:
C=[1 2 3;4 5 6;7 8 9]
C =
1 2 3
4 5 6
7 8 9.
2. Создание матриц специального вида. В математике встречаются матрицы специального вида, часто используемые при решении прикладных задач. Ниже приведен ряд из них.
Единичная матрица, рис. 5, а. В единичной матрице все элементы
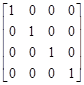
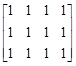
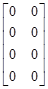
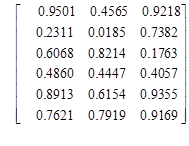
а б в г
Рис. 5. Специальные матрицы
равны нулю, кроме элементов стоящих на главной диагонали и равных единице. Для создания единичной матрицы необходимо подать команду
<Имя матрицы>=eye(<размер>).
Например: A = eye (4).
Единичная матрица может быть только квадратной.
Матрица со всеми единицами, рис. 5, б. Эта матрица содержит единицы во всех ячейках. Для создания матрицы необходимо указать
Имя матрицы=ones(Кол-во строк, Кол-во столбцов)
Например: A=ones(3, 4).
Нулевая матрица, рис. 5, в. Эта матрица содержит во всех своих ячейках одни нули. Для создания необходимо выполнить следующую команду:
Имя матрицы=zeros(кол-во строк, кол-во столбцов)
Например: A=zeros(4, 2).
Случайная матрица, рис. 5, г. Все значения этой матрицы получаются с генератора случайных чисел. Для создания такой матрицы необходимо задать следующую команду:
Имя матрицы=rand(кол-во строк, кол-во столбцов)
Например: A=rand(6, 3). По умолчанию в качестве элементов матрицы используются вещественные числа.
Доступ к ячейкам матрицы. Для доступа к ячейкам матрицы необходимо указать имя матрицы, номер строки и номер столбца. Нумерация строк и столбцов ведется с единицы. Номера пишутся в круглых скобках. Общий формат записи
Имя массива(номер строки, номер столбца)
Например: A(1,2).
Присвоение матрице математического выражения. Организация всех переменных системы Matlab как матрицы вызывает следующие ограничения применения их в выражениях.
Пример 3.
t =1:5
y = cos ( t )
t = 1 2 3 4 5
y = 0.5403 -0.4161 -0.9900 -0.6536 0.2837
y =[1 0.5 -0.4 -1 -0.6];
z=y/t
z =
-0.1127
Результат – единственное число, а не функция z(t)=cos(t)/t(!), как ожидалось. Причина этой ситуации в том, что обычные арифметические операции выполняются над числами, а ожидаемый результат требует выполнения операции над множеством значений (вектором).
Для организации поэлементного выполнения арифметических операций предусмотрена специальная форма их записи: «. op». Для приведенного выше примера применение операций деления одного массива на другой в виде «./» дает следующий результат:
t = 1:5;
y = [1 0.5 -0.4 -1 -0.6];
z = y./t
z = 1.0000 0.2500 -0.1333 -0.2500 -0.1200
Использование массивов рассмотрено в примере 4.
Пример 4. Использование массивов.
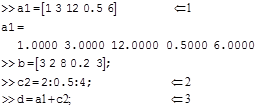
Комментарии к вычислениям:
 Элементы массива задаются в квадратных скобках и разделяются пробелами.
Элементы массива задаются в квадратных скобках и разделяются пробелами.
 Другой способ задать массив в виде x : y : z, где x – первый элемент массива, z – последний элемент массива, y – приращение каждого следующего элемента над предыдущим. Здесь элементами массива будут 2 2,5 3 3,5 4.
Другой способ задать массив в виде x : y : z, где x – первый элемент массива, z – последний элемент массива, y – приращение каждого следующего элемента над предыдущим. Здесь элементами массива будут 2 2,5 3 3,5 4.
 Сложение и вычитание массивов осуществляется поэлементно.
Сложение и вычитание массивов осуществляется поэлементно.
 Операции поэлементного умножения и деления массивов обозначаются:.* и . /
Операции поэлементного умножения и деления массивов обозначаются:.* и . /
 Взятие функции от каждого элемента массива. В результате получится массив той же размерности.
Взятие функции от каждого элемента массива. В результате получится массив той же размерности.
 Использование отдельных элементов массива. Номер элемента указывается после имени переменной массива в круглых скобках. Нумерация элементов начинается с единицы.
Использование отдельных элементов массива. Номер элемента указывается после имени переменной массива в круглых скобках. Нумерация элементов начинается с единицы.
 Сложение и умножение всех элементов массива на число.
Сложение и умножение всех элементов массива на число.
Программирование в Matlab
Основные понятия программирования . Выше было показано, что множество математических задач решается в системе Matlab без программирования – в командном режиме. Однако при решении серьезных задач возникает необходимость сохранения используемых последователь-ностей вычислений, а также их дальнейшей модификации. Иными словами, существует необходимость программи-рования решения задач. Она реализуется с помощью языка программирования системы.
Большинство объектов этого языка (команды, операторы и функции) одновременно являются объектами входного языка общения с системой в командном режиме работы.
В командном режиме результаты работы не сохраняются в памяти компьютера, хранятся только определения созданных в ходе их выполнения переменных и функций. А вот программы на языке программирования Matlab сохраняются в виде текстовых m-файлов. При этом могут сохраняться как целые программы в виде файлов-сценариев, так и отдельные программные модули – функции. Кроме того, важно, что программа может менять структуру алгоритмов вычислений в зависимости от входных данных и данных, создаваемых в ходе вычислений.
С позиций программиста язык программирования Matlab является типичным проблемно-ориентирован-ным языком программирования высокого уровня, содержащим сложные операторы (построения разнообраз-ных графиков, генерации матриц определенного вида и т. д.) и функции (матричные функции, функции быстрого преобразования Фурье и др.).
Основные средства программирования. Программами в системе Matlab являются m-файлы текстового формата. Язык программирования системы Matlab имеет следующие средства:
- данные различного типа;
- константы и переменные;
- операторы, включая операторы математических выражений;
- встроенные команды и функции;
- функции пользователя;
- управляющие структуры;
- системные операторы и функции;
- средства расширения языка.
Язык программирования Matlab является типичным интерпретатором. Это означает, что каждая инструкция программы распознается и тут же исполняется, что облегчает обеспечение диалогового режима общения с системой. Высокая скорость выполнения программ обеспечена наличием заведомо откомпилированного ядра, хранящего в себе критичные к скорости выполнения инструкции, такие как базовые математические и иные функции, а также тщательной отработкой системы контроля синтаксиса программ в режиме интерпретации.
Интерпретация означает, что Matlab не создает исполняемых конечных программ. Они существуют лишь в виде m-файлов. Для выполнения программ необходима среда Matlab. Однако для программ на языке Matlab созданы компиляторы, транслирующие программы Matlab в коды языков программирования С и C++. Это решает задачу создания исполняемых программ, первоначально разрабатываемых в среде Matlab. Компиляторы для системы Matlab являются вполне самостоятельными программными средствами и здесь не рассматриваются.
Структура типов данных системы Matlab представлена ниже:
В Matlab определены следующие основные типы данных, в общем случае представляющих собой многомерные массивы:
-single – числовые массивы с числами одинарной точности;
-double – числовые массивы с числами удвоенной точности;
-char – строчные массивы с элементами-символами;
-sparse – наследует свойства double, разреженные матрицы с элементами-числами удвоенной точности;
-сеll – массивы ячеек; ячейки, в свою очередь, тоже могут быть массивами;
-struct – массивы структур с полями, которые также могут содержать массивы;
-function_handle – дескрипторы функций:
-int32, uint32 – массивы 32-разрядных чисел со знаком и без знаков;
-int16, uint16 – массивы 16-разрядных целых чисел со знаком и без знаков;
-int8, uint8 – массивы 8-разрядных целых чисел со знаками и без знаков.
Кроме того, предусмотрен еще один тип данных – UserObject, который относится к типам данных (объектом), определяемым пользователем.
Каждому типу данных можно соотнести некоторые характерные для него операции, называемые методами.
Дочерние типы данных наследуют от последних их методы, что является признаком наследования объектов. Поскольку в иерархии типов данных сверху находятся данные типа array, то все виды данных в Matlab являются массивами.
Виды программирования. Язык программирования системы Matlab вобрал в себя все средства, необходимые для реализации различных видов программирования:
- процедурного;
- операторного;
- функционального;
- логического;
- структурного (модульного);
- объектно-ориентированного;
- визуально-ориентированного.
В основе процедурного, операторного и функциональ-ного типов программирования лежат процедуры, операторы и функции, используемые как основные объекты языка. Эти типы объектов присутствуют в Matlab.
Логическое программирование реализуется в Matlab с помощью логических операторов и функций. Это позволяет реализовать основные идеи логического программирова-ния, хотя на выдающуюся роль в этом классе языков программирования Matlab не претендует.
Matlab представляет собой яркий пример плодотворно-сти структурного программирования. Подавляющее боль-шинство функций и команд языка представляют собой вполне законченные модули, обмен данными между кото-рыми происходит через их входные параметры, хотя возможен обмен информацией и через глобальные переменные. Программные модули оформлены в виде текстовых m-файлов, которые хранятся на диске и подключаются к программам по мере необходимости. Важно отметить, что в отличие от многих языков программирования, применение тех или иных модулей не требует предварительного объявления, а для создания и отладки самостоятельных модулей Matlab имеет все необходимые средства. Подавляющее большинство команд и функций системы Matlab поставляется в виде таких модулей.
Объектно-ориентированное программирование также широко представлено в системе Matlab. Оно особенно актуально при программировании задач графики.
Что касается визуально-ориентированного программи-рования, то оно реализуется в пакете моделирования задан-ных объектов блоками устройств и систем Simulink.
Особенностью Matlab является двойственность операторов и функций. Многие операторы имеют свои аналоги в виде функций. Так, например, оператор «+» имеет аналог в виде функции sum. Команды, записанные в виде Commandargument нередко имеют форму записи и в виде функции:Command (' argument ')
Приемы разработки программ в Matlab в своей основной форме совпадают с аналогичными программами, разрабатываемыми в большинстве языков программиро-вания. Приведем некоторые примеры.
Цикл for…end. Для данного n, оператор
x=[];
fori =1:n
x=[x,i .2 ];
End x
или
x =[];
fori =1:n
x=[x,i .2 ];
End
x
создает определенный вектор размерности n, а оператор
x =[];
fori = n:1
x=[x,i .2 ];
End
x
создает вектор с теми же элементами, но размещенными в обратном порядке. Заметим, что матрица может быть пустой (например, в случае оператора x=[].)
Последовательность операторов
fori =1:m
forj =1:n
H(i,j)=1/(i+j-1);
End
End
H
создаст и напечатает на экране матрицу Гильберта размерности m×n. Точка с запятой, которая завершает внутренний оператор, предотвращает вывод на экран ненужных промежуточных результатов, в то время как последний оператор H выводит на экран окончательный результат.
Цикл while…end. В общем виде цикл whileзаписывается в виде
while<условие>
<операторы>
End
<Операторы>будут повторяться до тех пор, пока <условие>будет оставаться истинным. Например, для заданного числа a приведенная далее последовательность операторов вычислит и выведет на дисплей наименьшее неотрицательное число n, такое что 2 n <a:
n=0;
while 2 ^n <a
n=n +1;
End
n
Условный оператор if…end. В общем виде простой оператор if используется следующим образом:
if<условие>
<операторы>
End
<Операторы>будут выполняться, только если <условие>истинно. Возможно также множественное ветвление, что демонстрируется приведенным далее примером.
if n <0
parity =0;
elseif rem(n,2)==0
parity =2;
Else
parity =1;
End
При использовании двухвариантного условного оператора часть, связанная с elseif, конечно, не используется.
Оператор переключения case…end. При необходимости построить конструкцию ветвления с более чем двумя логическими условиями удобнее использовать не вложенные операторы if, а оператор переключения switch ...case. Этот оператор имеет следующую структуру:
switch<выражение>
%<выражение>-это обязательно скаляр или строка
case<значение1>
Операторы
%выполняется, если <выражение>=<значение1>
case<значение2>
Операторы
%выполняется, если <выражение>=<значение2>
...
Otherwise
Операторы
%выполняется, если <выражение>не совпало
%ни с одним значением
End
В Matlabиспользуются следующие операторы отношения:
| Обозначение
| Значение
|
| <
| меньше чем
|
| >
| больше чем
|
| <=
| меньше или равно
|
| >=
| больше или равно
|
| ==
| равно
|
| ~ =
| не равно
|
Отметим, что знак «=» используется в операторах присваивания, в то время как знак «==» используется в операторах отношения.
Операторы отношения (или, другими словами, логические переменные, которые они создают) могут объединяться с помощью логических операторов:
| Обозначение
| Значение
|
| &
| И
|
| |
| ИЛИ
|
| ~
| НЕ
|
Когда эти операторы применяются к скалярам, то результатом является тоже скаляр 1 или 0 в зависимости от того, является ли результат истиной или ложью. Например,
3<5
ans = 1
3>5
ans = 0
Когда операторы отношения применяются к матрицам одного размера, результатом является матрица того же размера, у которой в качестве элементов стоят 0 или 1, в зависимости от соотношения между соответствующими элементами исходных матриц. Например,
a=rand(5); b=triu(a); a==b
ans =
1 1 1 1 1
0 1 1 1 1
0 0 1 1 1
0 0 0 1 1
0 0 0 0 1.
Операторы while и if интерпретируют отношение между матрицами как истинное в том случае, если результирующая матрица не имеет нулевых элементов.
Так, если необходимо выполнить оператор в том случае, когда матрицы A и B полностью совпадают, можно написать
if A ==B < операторы >end,
но если необходимо выполнить оператор в том случае, когда матрицы A и B не равны, следует ввести
if any(any(A .=B))< оператор >end
или, что проще,
ifA == Belse <оператор> end.
Заметим, что конструкция
ifA .= B <оператор> end
почти наверняка не даст того, что нужно, поскольку оператор будет выполняться, только если каждый элемент матрицы A будет отличаться от соответствующего элемента матрицы B. Для сведения матричных отношений к вектору или скаляру можно воспользоваться функциями any и all. В предыдущем примере необходимо использование функции any два раза, поскольку эта функция – векторная.
Функция find. Оператор k = find(x) возвращает вектор k номеров ненулевых элементов вектора/матрицы x. Если x – матрица, то при определении индексов она рассматри-вается как вектор, образованный последовательно соединенными столбцами матрицы. Вектор find(x) можно использовать совместно с операторами отношения, поскольку результатом применения оператора отношения к матрицам является матрица из 0 и 1 (ложь или истина). Таким образом, можно с помощью одного оператора find определить и записать сразу все индексы матрицы, удовлетворяющие некоторому условию. Если при этом вспомнить, что оператор цикла for допускает форму for k=KK , где KK – целый вектор, то удобно использовать их вместе. Например, если необходимо выполнить <оператор>только для тех элементов матрицы, которые больше 3 , то удобно это сделать следующим образом:
fori = find ( A >3)
<оператор>
E nd
При отладке выражений и программ в окне Редактора-отладчика сообщения об ошибках выдаются в командное окно MATLAB.
М-файлы бывают двух типов: сценарии (скрипты) и функции. Для их создания необходимо вызвать редактор m-файлов командой edit в командном окне либо последовательностью File - New - M - file из меню командного окна.
M-файл-сценарий , называемый также Script-файлом, является простой записью серии команд без входных и выходных параметров. Он имеет следующую структуру:
%Основной комментарий
%Дополнительный комментарий





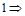 Если в конце строки ставится точка с запятой, то результат не будет выведен после нажатия Enter.
Если в конце строки ставится точка с запятой, то результат не будет выведен после нажатия Enter. Здесь нет точки с запятой, и после нажатия Enter результат выводится и присваивается переменной c.
Здесь нет точки с запятой, и после нажатия Enter результат выводится и присваивается переменной c.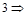 Для того чтобы узнать значение переменной достаточно ввести ее имя в командную строку и нажать Enter.
Для того чтобы узнать значение переменной достаточно ввести ее имя в командную строку и нажать Enter.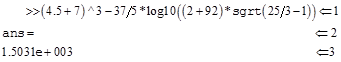
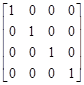
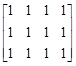
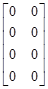
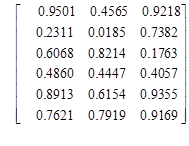
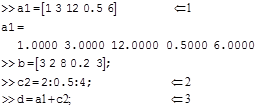
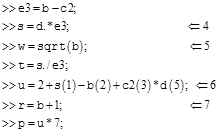
 Операции поэлементного умножения и деления массивов обозначаются:.* и . /
Операции поэлементного умножения и деления массивов обозначаются:.* и . / Взятие функции от каждого элемента массива. В результате получится массив той же размерности.
Взятие функции от каждого элемента массива. В результате получится массив той же размерности. Использование отдельных элементов массива. Номер элемента указывается после имени переменной массива в круглых скобках. Нумерация элементов начинается с единицы.
Использование отдельных элементов массива. Номер элемента указывается после имени переменной массива в круглых скобках. Нумерация элементов начинается с единицы. Сложение и умножение всех элементов массива на число.
Сложение и умножение всех элементов массива на число.

