Частотных характеристик передаточных функций

 

Цель работы: Изучить принципы построения частотных характеристик передаточных функций в программе MATLAB .

Задание:

а) по заданному преподавателем варианту (см. таблицу 1) построить график АЧХ передаточной функции.

в). построить график ФЧХ передаточной функции.

с). построить графики АФЧХ передаточной функции.

Таблица 1.

№ п/п	Функция
1	W=1/(5s3+25s2+12s+2)
2	W=1/(12s3+30s2+12s+1)
3	W=2/(10s3+20s2+10s+1)
4	W=3/(5s3+30s2+7s+1)
5	W=1/(7s3+20s2+2s+1)
6	W=4/(12s3+10s2+12s+2)
7	W=2/(5s3+20s2+7s+1)
8	W=3/(12s3+20s2+5s+3)
9	W=2/(10s3+30s2+10s+1)
10	W=1/(20s3+20s2+12s+1)
11	W=2/(15s3+30s2+10s+1)
12	W=1/(30s3+20s2+12s+2)
13	W=1/(15s3+10s2+25s+1)
14	W=1/(5s3+25s2+10s+2)
15	W=2/(30s3+10s2+25s+2)
16	W=2/(5s3+10s2+7s+1)
17	W=3/(12s3+15s2+15s+3)
18	W=2/(10s3+30s2+10s+1)
19	W=1/(20s3+20s2+20s+1)
20	W=2/(15s3+30s2+10s+1)
21	W=1/(30s3+20s2+30s+2)
22	W=1/(15s3+5s2+10s+1)

Основные положения

Частотные характеристики моделей, которые описаны соответствующими передаточными функциями, изучают, подавая на вход гармонический сигнал и измеряя величину амплитуды и сдвига фаз на выходе. Возьмём нижеследующую передаточную функцию второго порядка и в программе Simulink подадим на вход гармонический сигнал, изменяющийся по частоте (Рис.1).

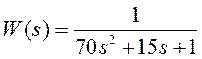
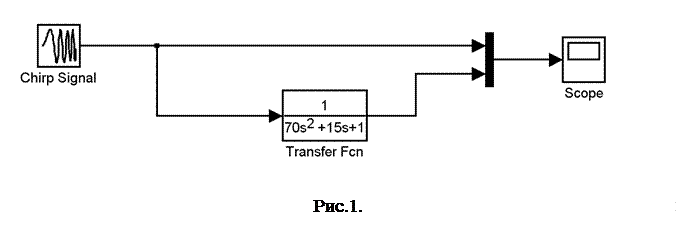
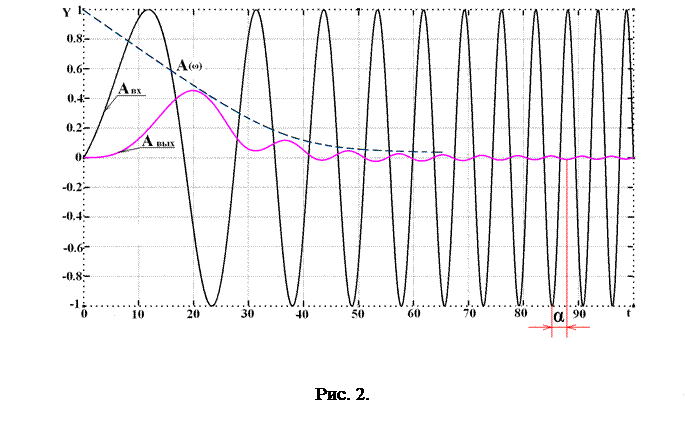Результаты моделирования показаны на рисунке 2. На входе амплитуда сигнала остаётся постоянной, а на выходе наблюдается её уменьшение, в зависимости от частоты 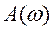. Кроме того, при увеличении частоты гармонического сигнала, сдвиг фаз между входным и выходным сигналами увеличивается   α(ω). Эти качественные характеристики хорошо видны на рисунке 2, но хотелось бы оценить их количественно. Математики нашли возможность оценить графически обе характеристики одновременно на комплексной плоскости. Впервые прямоугольную систему координат ввел француз Рене Декарт в своей работе «Рассуждение о методе» в 1637 году.

Как же передаточную функцию представить на комплексной плоскости. Рассмотрим передаточную функцию 1-го порядка:

 

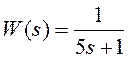
Подставим 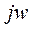  вместо s.

W(jw)=1/(5jw+1)

Умножим числитель и знаменатель на комплексно сопряжённое число

 

W(jw)=1/(5jw+1)=(5jw-1)/(5jw+1)(5jw-1)=(5jw-1)/(-25w²-1)

 

Поменяем знак в числителе и знаменателе.

 

W(jw)=1/(25jw+1)-5jw/(25jw+1)

В результате получили действительное и мнимое число.

 

Re(jw)= 1/(25w²+1)

Im(jw)= -5jw/(25w²+1)

 

 

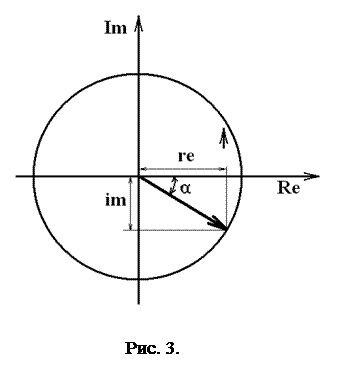
На рисунке 3 показана комплексная плоскость и полученные действительное re и мнимое число im для какой то определенной частоты w.

Для этой частоты можно рассчитать амплитуду сигнала a=sqrt(re.^2+im.^2) и сдвиг фаз α = atan(im./re);

 

В программе Matlab можно задать изменение частоты, рассчитать амплитуду и сдвиг фаз и построить график на комплексной плоскости.

 

w=0.001:.01:9;

re= 1./(25.*w.^2+1);

im= -5.*w./(25.*w.^2+1);

a=sqrt(re.^2+im.^2);

fi=atan(im./re);

fig=360*fi/6.28

plot(re,im),grid on

 

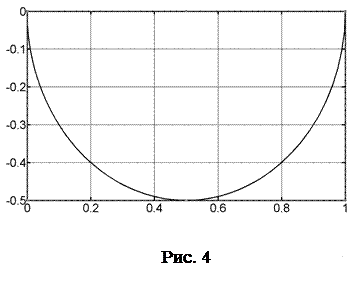
На рисунке 4 показан результат работы этой программы.

Конечно, можно напечатать график зависимости амплитуды от частоты a(w) (plot(w,a),grid on) и сдвига фаз от частоты fig(w) (plot(w,fig),grid on),                          который в программе из радиан преобразован в градусы. Как видно из графика на рисунке 4, амплитуда с ростом частоты убывает и стремится к нулю при увеличении частоты до ∞ для передаточной функции первого порядка, а угол сдвига фаз изменяется от нуля до 90^о.

В программе Matlab есть для частотных исследований очень удобная функция F= freqs(num,den,w), где:

num – числитель передаточной функции,

den – знаменатель передаточной функции,

w – частота.

Здесь не нужно заменять оператор Лапласа на jw, а затем умножать числитель и знаменатель на комплексно сопряжённое число, что достаточно сложно уже для передаточных функций, начиная с четвертого порядка.

Используя функцию freqs(num,den,w), напишем программу Для расчета частотных характеристик передаточных функций.

 

w=0.0001:.001:9

den=[5 1];

num=[1];

ob=freqs(num,den,w);

v=imag(ob);                     % расчет мнимой части

u=real(ob);                  % расчет действительной части

f=atan(v./u);                 % расчет угла сдвига в радианах

a=sqrt(u.^2+v.^2);            % расчет амплитуды

for i=1:2000 %

ug(i)=360*f(i)/6.28;   % расчет угла сдвига в градусах

if f(i)>0

ug(i)=360*f(i)/6.28-180; % расчет угла сдвига в градусах >180^о

end

am(i)=sqrt(u(i).^2+v(i).^2);   % расчет амплитуды

end

plot(u,v),grid on               % построение АФЧХ

 

При выполнении этой программы будет построен график, показанный на рисунке 4, то есть результат достигнут более быстрым способом. Тем более он удобен, если передаточная функция имеет более высокий порядок.

Содержание отчета:

1. График АЧХ передаточной функции..

2. График ФЧХ передаточной функции..

3. Графики  АФЧХ передаточных функций, полученных путём снижения порядка до первого, начиная с заданного по варианту.

Например:

a)W1=3/(12s³+20s2+5s+3)

b) W2=3/(20s2+5s+3)

c) W3=3/(5s+3)

 

4.  Выводы к каждому графику.

 

 

ЛАБОРАТОРНАЯ РАБОТА №6