Цель работы: Изучить прямое и обратное преобразование Лапласа, принципы получения передаточных функций и математические операции с ними в программе Matlab.
Задание:
а) По заданному преподавателем варианту (см. таблицу 4.1) выполнить последовательное, параллельное и встречно-параллельное соединение передаточных функций.
б) Получить графики переходных процессов для всех вариантов соединения.
в) Сделать выводы по работе.
Основные положения
Элементы систем автоматического регулирования обычно описываются передаточными функциями.
Передаточной функцией называется отношение изменения выходной величины к изменению входной, преобразованной по Лапласу.
Дифференциальное уравнение, представляющее математическую модель системы регулирования имеет следующий вид:
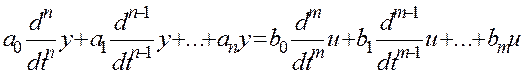 (4.1)
(4.1)
Где 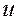 и
и 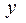 - входной и выходной сигналы системы регулирования.
- входной и выходной сигналы системы регулирования.
Преобразование Лапласа выполняется с помощью формулы:
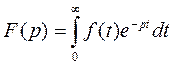
f(t) – оригинал
F(p) – изображение по Лапласу
В операторной форме это уравнение (1) будет следующим:
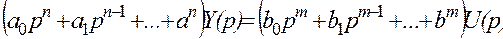 , (4.2)
, (4.2)
где, – 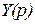 ,
, 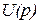 – изображение входного и выходного сигналов.
– изображение входного и выходного сигналов.
Определим передаточную функцию системы регулирования:
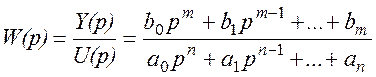 . (4.3)
. (4.3)
Порядок числа n больше или равно m.
Рассмотрим несколько простых уравнений.
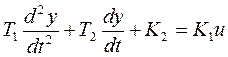 (4.4)
(4.4)
Преобразуем по Лапласу.
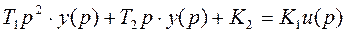 (4.5)
(4.5)
Найдём передаточную функцию
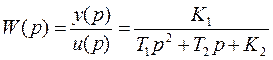 (4.6)
(4.6)
Те же операции проделаем и с уравнениями (4.7), (4.10), (4.13).
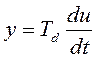 (4.7)
(4.7)
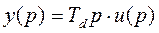 (4.8)
(4.8)
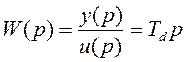 (4.9)
(4.9)
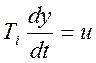 (4.10)
(4.10)
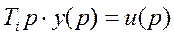 (4.11)
(4.11)
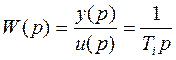 (4.12)
(4.12)
 (4.13)
(4.13)
W(p)=K (4.14)
В программе Matlab передаточные функции создаются достаточно легко в строке команд. Например, если в уравнении (4.4) коэффициенты Т1, Т2, К2, К1 равны 2, 5, 1 и 1, то выполняется следующая операция:
>> w1=tf(1,[2 5 1])
Transfer function:
1
---------------
2 s^2 + 5 s + 1
>>
В англоязычных странах оператор Лапласа (p) обозначается (s).
Для уравнения (4.7) при 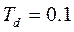
>> w2=tf([.1 0],[1])
Transfer function:
0.1 S
>>
С передаточными функциями работать значительно проще, чем с дифференциальными уравнениями. Их можно складывать, вычитать, умножать и делить, чтобы потом выполнить обратное преобразование Лапласа (4.15) и получить результирующее уравнение.
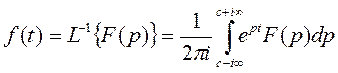 (4.15)
(4.15)
В Matlab имеются соответствующие функции прямого «laplace» и обратного преобразования Лапласа «ilaplace». Вычисления выполняются в символьной форме.
Примеры:
>> syms a t w s
>> laplace(exp(-a*t),t,s)
ans =
1/(s+a)
>> w=laplace(exp(-a*t),t,s)
w =
1/(s+a)
>> h=ilaplace(w,s,t)
h =
exp(-a*t)
>>
Как видно, вычисления выполняются корректно и совпадают с табличными.
Арифметические действия (+, -, /, *) с передаточными функциями могут быть выполнены в Matlab.
Пример: Рассмотрим две передаточные функции:
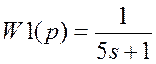
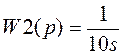
Получим их в строке команд Matlab.
>> w2
Transfer function:
1
----
10 s
>> w1=tf(1,[5 1])
Transfer function:
1
-------
5 s + 1
Выполним сложение.
>> w3=w1+w2
Transfer function:
15 s + 1
-------------
50 s^2 + 10 s
Тот же результат можно получить, применив оператор «parallel» вместо «+», что соответствует правилу сложения передаточных функций при их параллельном соединении.
Перемножим заданные функции:
>> w4=w1*w2
Transfer function:
1
-------------
50 s^2 + 10 s
Это же значение можно получить, применив оператор «series» вместо «*», что соответствует правилу умножения передаточных функций при их последовательном соединении.
Если эти передаточные функции соединяются встречно-параллельно (Рис.4.1), то результирующая передаточная функция вычисляется по формуле:
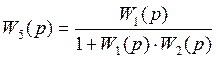 (4.16)
(4.16)
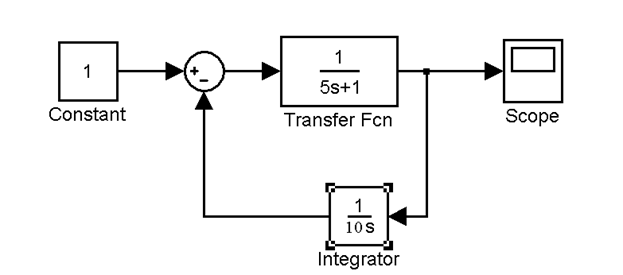
Знак «+» в знаменателе при отрицательной обратной связи и знак «-» при положительной.
В программе Matlab для этой операции есть оператор «feedback».
>> w5=feedback(w1,w2)
Transfer function:
10 s
-----------------
50 s^2 + 10 s + 1
Если положительная обратная связь, то в скобках добавляется «-1».
>> w5=feedback(w1,w2, -1)
Для полученных в результате всех операций функций можно построить их графики, если аргументом будет единичное ступенчатое возмущение. Для этого в программе Matlab предусмотрен оператор «step».
>> step(w3),grid on
Результат на рисунке 4.2.
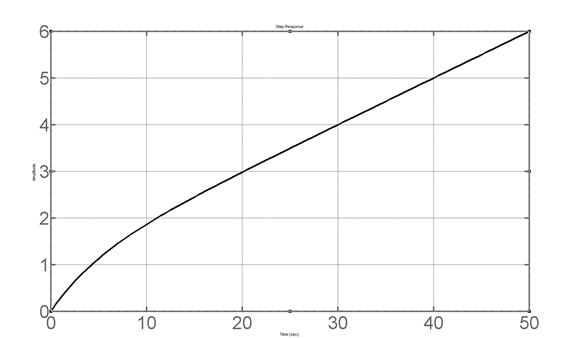
>> step(w4),grid on
Результат на рисунке 4.3.
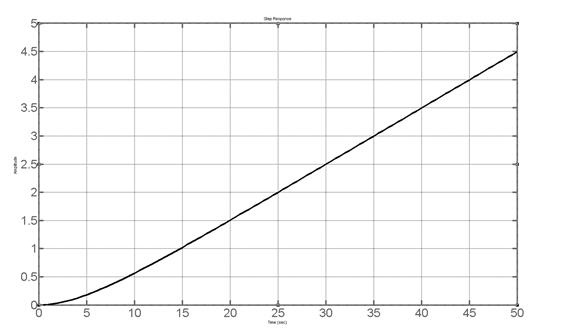
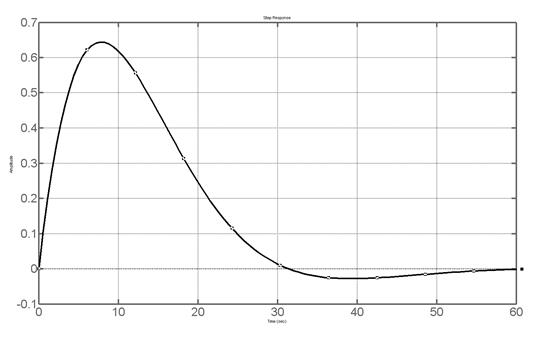
>> step(w5),grid on
>>
Результат на рисунке 4.4.
Порядок выполнения работы
1) По заданному преподавателем варианту (см. таблицу 4.1) выполнить последовательное, параллельное и встречно-параллельное соединение передаточных функций.
2) Получить последовательное, параллельное и встречно-параллельное соединение передаточных функций.
графики переходных процессов для всех вариантов соединения.
3) Скопировать результаты работы в файл формата *.doc для предъявления отчета и защиты работы.
4) В отчете сделать выводы по работе
Таблица 4.1
| Вариант
| Функции
| Параметры
|
| 1
| 1-я (4.4), 2-я (4.10)
| Т1=2, Т2=4, К2=1, К1=2, Ti=12
|
| 2
| 1-я (4.4), 2-я (4.10+4.13)
| Т1= 1, Т2= 5, К2=1, К1= 1, Ti=12, K=5.
|
| 3
| 1-я (4.4), 2-я (4.10+4.13)
| Т1= 1, Т2= 15, К2= 5, К1= 1, Ti=7, K=9.
|
| 4
| 1-я (4.4), 2-я (4.7+4.13)
| Т1=1, Т2=5, К2=1, К1=1, Td=0. 2, K=5.
|
| 5
| 1-я (4.4), 2-я (4.7+4.13)
| Т1= 2, Т2= 10, К2= 2, К1=1, Td=0. 1, K=15.
|
| 6
| 1-я (4.4), 2-я (4.13+4.10)
| Т1=0. 2, Т2=5, К2= 2, К1=1, Ti=1 5, K= 2.
|
| 7
| 1-я (4.4), 2-я (4.10+4.13)
| Т1= 0.5, Т2= 25, К2=1, К1= 2, Ti= 25, K= 15.
|
| 8
| 1-я (4.4), 2-я (4.13+4.10)
| Т1= 0.1, Т2= 7, К2= 0.1, К1=1, Ti=12, K=1.
|
| 9
| 1-я (4.4), 2-я (4.13+4.7)
| Т1=2, Т2=3, К2=3, К1=1, Td=0. 1, K= 15.
|
| 10
| 1-я (4.4), 2-я (4.13+4.7)
| Т1=0.5, Т2=5, К2=1, К1=3, Td=0.2, K= 7.
|
| 11
| 1-я (4.4), 2-я (4.10+4.13)
| Т1=1, Т2= 25, К2= 3, К1=1, Ti=1 0, K= 1.
|
| 12
| 1-я (4.4), 2-я (4.7+4.13)
| Т1= 2, Т2= 10, К2= 2, К1=1, Td=0. 1, K=15.
|
| 13
| 1-я (4.4), 2-я (4.10+4.13)
| Т1= 1, Т2= 5, К2=1, К1= 1, Ti=12, K=5.
|
| 14
| 1-я (4.4), 2-я (4.7+4.13)
| Т1= 2, Т2= 10, К2= 2, К1=1, Td=0. 1, K=15.
|
| 15
| 1-я (4.4), 2-я (4.10+4.13)
| Т1= 1, Т2= 50, К2=1 0, К1= 1, Ti=22, K=2.
|
| 16
| 1-я (4.4), 2-я (4.7+4.13)
| Т1= 2, Т2= 10, К2= 2, К1=1, Td=0. 1, K=1 1.
|
| 17
| 1-я (4.4), 2-я (4.10+4.13)
| Т1=1, Т2=50, К2=1. 2, К1=1, Ti=30, K=5.
|
| 18
| 1-я (4.4), 2-я (4.7+4.13)
| Т1=2, Т2=10, К2=2, К1=1, Td=0.1, K=1.
|
| 19
| 1-я (4.4), 2-я (4.10+4.13)
| Т1=1, Т2=23, К2=1.5, К1=1, Ti=10, K=7.
|
| 20
| 1-я (4.4), 2-я (4.7+4.13)
| Т1=0.4, Т2=10, К2=6, К1=1, Td=0.1, K=12.
|
| 21
| 1-я (4.4), 2-я (4.10+4.13)
| Т1=1, Т2=21, К2=1, К1=1, Ti=1 7, K=5.
|
| 22
| 1-я (4.4), 2-я (4.7+4.13)
| Т1=0.3, Т2=10, К2=2. 5, К1=1, Td=0.1, K=3.
|
| 23
| 1-я (4.4), 2-я (4.10+4.13)
| Т1=0.2, Т2=16, К2=2, К1=1, Ti=15, K=2.
|
| 24
| 1-я (4.4), 2-я (4.7+4.13)
| Т1=2, Т2=10, К2=2, К1=1, Td=0.1, K=12.
|
| 25
| 1-я (4.4), 2-я (4.10)
| Т1=1, Т2=5, К2=1, К1= 2, Ti=12, K=25.
|
Содержание отчета:
1. Передаточные функции при последовательном, параллельном и встречно-параллельном соединении заданных передаточных функций.
2. Графики полученных передаточных функций с четкой оцифровкой осей координат.
3. Выводы по работе.
ЛАБОРАТОРНАЯ РАБОТА №5
Исследование





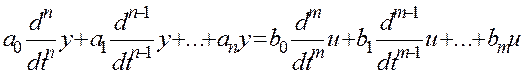 (4.1)
(4.1)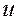 и
и 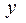 - входной и выходной сигналы системы регулирования.
- входной и выходной сигналы системы регулирования.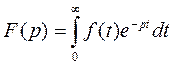
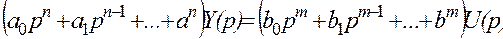 , (4.2)
, (4.2)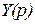 ,
, 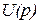 – изображение входного и выходного сигналов.
– изображение входного и выходного сигналов.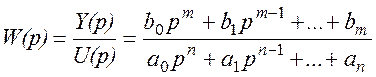 . (4.3)
. (4.3)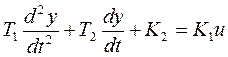 (4.4)
(4.4)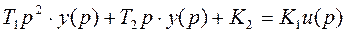 (4.5)
(4.5)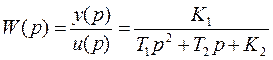 (4.6)
(4.6)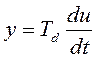 (4.7)
(4.7)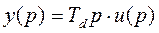 (4.8)
(4.8)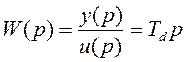 (4.9)
(4.9)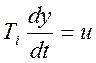 (4.10)
(4.10) 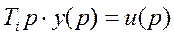 (4.11)
(4.11)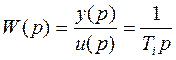 (4.12)
(4.12) (4.13)
(4.13) 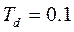
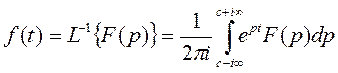 (4.15)
(4.15)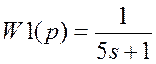
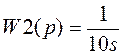
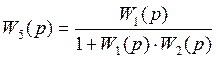 (4.16)
(4.16)






