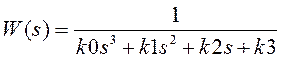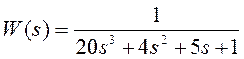Влияние распределения корней на вид переходного

Процесса передаточных функций

 

Цель работы: Изучить влияние распределения корней на вид переходного процесса передаточных функций  в программе MATLAB .

Задание:

По заданному преподавателем варианту (см. таблицу 1)  найти корни передаточных функций и построить графики переходных функции.

 

Таблица 1.

№ п/п	Функция
1	W=1/(5s3+25s2+12s+2)
2	W=1/(12s3+30s2+12s+1)
3	W=2/(10s3+20s2+10s+1)
4	W=3/(5s3+30s2+7s+1)
5	W=1/(7s3+20s2+2s+1)
6	W=4/(12s3+10s2+12s+2)
7	W=2/(5s3+20s2+7s+1)
8	W=3/(12s3+20s2+5s+3)
9	W=2/(10s3+30s2+10s+1)
10	W=1/(20s3+20s2+12s+1)
11	W=2/(15s3+30s2+10s+1)
12	W=1/(30s3+20s2+12s+2)
13	W=1/(15s3+10s2+25s+1)
14	W=1/(5s3+25s2+10s+2)
15	W=2/(30s3+10s2+25s+2)
16	W=2/(5s3+10s2+7s+1)
17	W=3/(12s3+15s2+15s+3)
18	W=2/(10s3+30s2+10s+1)
19	W=1/(20s3+20s2+20s+1)
20	W=2/(15s3+30s2+10s+1)
21	W=1/(30s3+20s2+30s+2)
22	W=1/(15s3+5s2+10s+1)

Общие положения

Повторим, что переходной функцией называется реакция объекта, описанного передаточной функцией W(s), на единичное ступенчатое воздействие. Для её получения в программе Matlab имеется специальная функция step(w(s)).

Установлено, что переходная функция будет сходящейся (амплитуда убывает со временем), если корни передаточной функции будут находиться в левой части комплексной плоскости, то есть все они отрицательны. На рисунке 1 это a1, a2+b, a2-b.

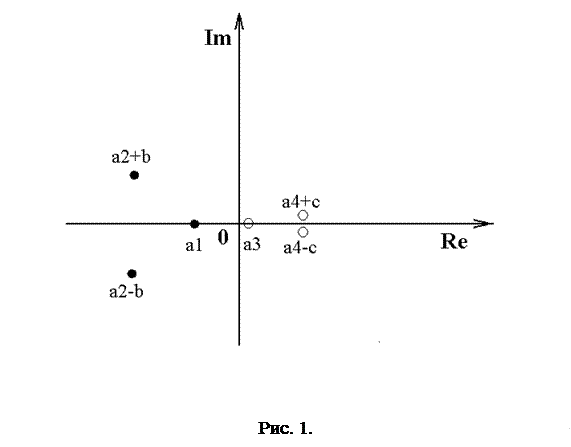Если хотя бы один из них положителен, то переходный процесс будет расходящимся. На рисунке 1 это a3, a4+с, a4-с. Если корень находится на мнимой оси, то переходный процесс будет гармоническим с постоянной амплитудой.

Исследуем следующую передаточную функцию:

 

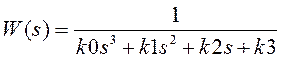
Момент перехода процесса из сходящегося в расходящийся для передаточной функции третьего порядка W(s) можно определить из следующего условия:

k1*k2 = k0*k3

 

Если  k1*k2 > k0*k3, то переходный процесс сходящийся, а если k1*k2 < k0*k3, то переходный процесс расходящийся.

Рассмотрим пример:

 

 

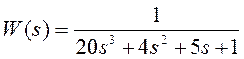
Напишем программу для вычисления корней и построения переходной функции.

 

 

num=[1];                  % числитель передаточной функции

den=[20 4 5 1];       % знаменатель передаточной функции

w=tf(num,den);       % определение передаточной функции

pole(w)                     % вычисление корней передаточной функции

step(w,150,'k'),grid on % построение графика переходной функции

 

 

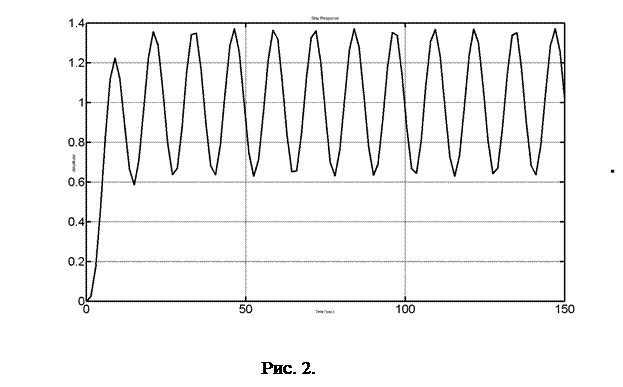
Корни передаточной функции напечатаны в окне команд:

 

ans =

 

0.0000 + 0.5000i

0.0000 - 0.5000i

-0.2000         

 

Как видим, мнимые корни находятся на мнимой оси и переходная функция имеет гармонический характер с незатухающей амплитудой.

Изменим коэффициент при первой производной с 5 на 7.

 

 

num=[1];                  % числитель передаточной функции

den=[20 4 7 1];       % знаменатель передаточной функции

w=tf(num,den);       % определение передаточной функции

pole(w)                     % вычисление корней передаточной функции

step(w,150,'k'),grid on % построение графика переходной функции

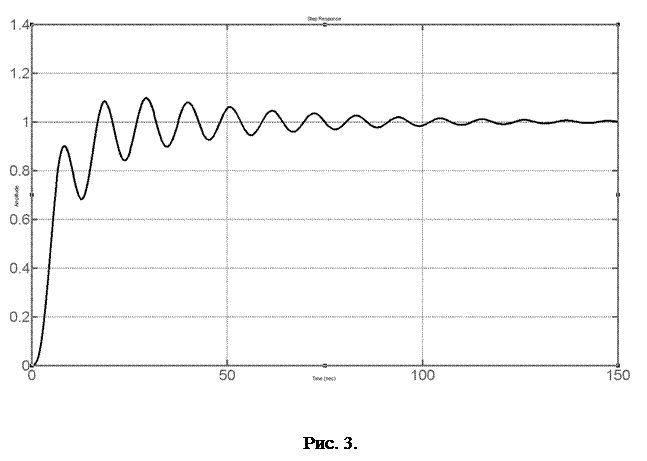
Все корни, в этом случае, оказываются отрицательными,

 

-0.0269 + 0.5843i

-0.0269 - 0.5843i

-0.1461   

 

Переходный процесс, показанный на рисунке 3, в этом случае, сходящийся, то есть амплитуда колебаний со временем уменьшается.

 

Содержание отчета:

3. График переходной  функции по заданию и расчет корней.

4. График сходящейся переходной функции, найденной путем изменения коэффициентов знаменателя передаточной функции  и расчет корней

5.  График расходящейся переходной функции, найденной путем изменения коэффициентов знаменателя передаточной функции и расчет корней

4.  Выводы к каждому графику.