№2.1 Дана матрица выигрышей первого игрока в матричной игре
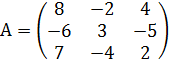 .
.
Для этой игры
· Проверить наличие седловой точки;
· По возможности уменьшить размерность матрицы игры;
· Графически найти оптимальные стратегии обоих игроков и цену игры;
· Свести нахождение оптимальных стратегий обоих игроков к двойственной паре задач линейного программирования. Решить обе и указать оптимальные стратегии обоих игроков.
Решение:
а) Анализ матрицы платежей (матрицы игры).
Первому игроку соответствуют строки матрицы, он имеет три возможности (чистых стратегий). Если первый игрок выберет свою первую возможность, то из первой строки следует: при выборе противником его первой возможности первый игрок выиграет (а второй проиграет) 8 ден. ед.; при выборе противником второй возможности первый игрок проиграет (а второй выиграет) 2 ден. ед.; при выборе противником третьей возможности выигрыш первого игрока составит 4 ден. ед. Аналогичный смысл у второй и третьей строк матрицы.
При этом матрица выигрышей второго игрока отличается знаками тех же элементов, а если второму будут соответствовать строки матрицы, то и транспонированием матрицы платежей, 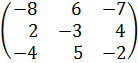 ;
;
б) Проверка наличия седловой точки в матричной игре:
В первой строке минимальное значение -2, во второй -6 и в третьей -4. Тогда нижняя цена игры (максимин) 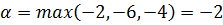 ;
;
В первом столбце максимальное значение 8, во втором 3 и в третьем 4. Тогда верхняя цена игры (минимакс) 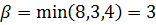 .
.
Если бы получили, что 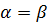 , то игра имела бы седловую точку и оптимальные стратегии обоих игроков были бы чистыми с постоянным выбором той возможности, где достигаются
, то игра имела бы седловую точку и оптимальные стратегии обоих игроков были бы чистыми с постоянным выбором той возможности, где достигаются 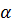 по строкам и
по строкам и 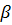 по столбцам. При этом обоим игрокам будет невыгодно отклоняться от этих оптимальных стратегий – при этом первый игрок может выиграть меньше и второй игрок может проиграть больше значения
по столбцам. При этом обоим игрокам будет невыгодно отклоняться от этих оптимальных стратегий – при этом первый игрок может выиграть меньше и второй игрок может проиграть больше значения 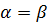 , которое являлось бы ценой игры.
, которое являлось бы ценой игры.
Здесь 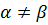 , тогда игра не имеет седловой точки, тогда оптимальные стратегии обоих игроков смешанные (содержат несколько возможностей). При этом цена игры, как средний платёж первого игрока при оптимальных стратегиях игроков в большом числе таких игр, будет между
, тогда игра не имеет седловой точки, тогда оптимальные стратегии обоих игроков смешанные (содержат несколько возможностей). При этом цена игры, как средний платёж первого игрока при оптимальных стратегиях игроков в большом числе таких игр, будет между 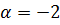 и
и 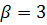 ;
;
в) Проверим возможность уменьшения размерности матрицы платежей.
в.1) Если все элементы одной строки больше соответствующих элементов другой строки, то первая из них преобладает над второй. В таком случае первому игроку применять вторую из этих возможностей невыгодно, в его смешанной стратегии доля применения такой возможности будет нулевой и такую строку можно удалить из рассмотрения при поиске оптимальной смешанной стратегии.
Здесь при сравнении первой и второй строк видно, что ни одна не преобладает над другой; аналогично для второй и третьей строк. А вот при сравнении первой и третьей строк видно, что первая преобладает над третьей. Тогда третью строку удалим из рассмотрения до получения оптимальной стратегии, в которой добавится нулевая третья составляющая, получим матрицу игры
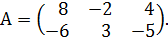
в.2) Если один столбец преобладает над другим, то второму игроку невыгодно применять преобладающий столбец и его возможность. Здесь в любой паре столбцов матрицы А есть и меньшие и большие соответствующие элементы, преобладания столбцов нет;
г) При получении двух строк (или двух столбцов) в матрице игры можно оптимальную смешанную стратегию игроков найти графически.
г.1) Здесь матрица А имеет две строки, будем искать смешанную стратегию первого игрока в виде 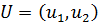 при условиях
при условиях 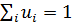 и
и 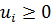 . Значение
. Значение 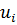 даёт вероятность (относительную частоту) применения возможности с номером
даёт вероятность (относительную частоту) применения возможности с номером 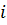 при большом числе игр.
при большом числе игр.
Для нахождения этих двух составляющих на горизонтальной оси отложим две точки на расстоянии 1, они будут соответствовать этим чистым возможностям. Через эти точки проведём две вертикальные оси с одинаковым масштабом. Каждый столбец матрицы А даёт координаты точек на первой и второй вертикали, 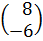 ,
, 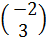 ,
, 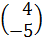 и такие точки попарно соединим прямыми линиями, см. Рисунок 3.а. Для первого игрока на построенном горизонтальном отрезке находим область, точки которой лежат не выше каждой из построенных прямых. Здесь верхней границей области будет ломаная МКТР (при большем числе столбцов матрицы А ломаная может быть более сложного вида).
и такие точки попарно соединим прямыми линиями, см. Рисунок 3.а. Для первого игрока на построенном горизонтальном отрезке находим область, точки которой лежат не выше каждой из построенных прямых. Здесь верхней границей области будет ломаная МКТР (при большем числе столбцов матрицы А ломаная может быть более сложного вида).
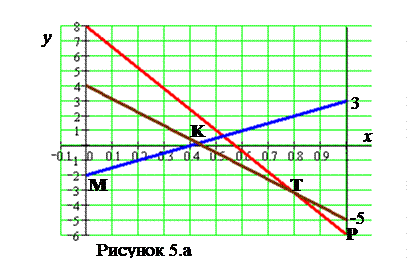
Среди точек полученной области и её границы МКТР (верхней границы выигрыша) на Рисунке 5.а наибольшую ординату имеет точка К. Точка К является пересечением второй и третьей прямых, что приводит к системе
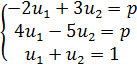
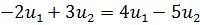 ,
,  ,
, 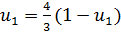 ,
, 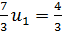 ,
, 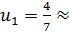 0.5714; Тогда
0.5714; Тогда 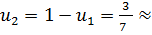 0.4286; В исходной задаче с тремя возможностями первого игрока
0.4286; В исходной задаче с тремя возможностями первого игрока 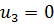 . При этом цена игры
. При этом цена игры 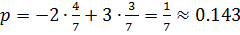 .
.
Получили, что первый игрок в большой серии игр должен в 57,14% применять первую возможность, в 42,86% вторую и не использовать третью. Если и противник будет применят свою оптимальную стратегию, то за 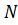 игр средний выигрыш будет практически равен
игр средний выигрыш будет практически равен 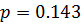 и его общий выигрыш станет около
и его общий выигрыш станет около 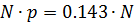 ден.ед.
ден.ед.
Отклонение первого игрока от своей оптимальной стратегии может привести к снижению общего выигрыша, а отклонение второго игрока от своей оптимальной стратегии может привести к увеличению общего выигрыша в серии игр;
г.2) После нахождения оптимальной стратегии первого игрока можно графическим методом найти оптимальное решение и второго игрока.
Второй игрок имеет три возможности, его смешанная стратегия виде 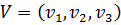 при условиях
при условиях 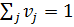 и
и 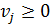 . Значение
. Значение 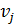 даёт вероятность (относительную частоту) применения возможности с номером
даёт вероятность (относительную частоту) применения возможности с номером 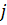 второго игрока при большом числе игр. В следующей пункте рассмотрим общий метод нахождения оптимальных стратегий обоих игроков через решение двойственной пары задач линейного программирования.
второго игрока при большом числе игр. В следующей пункте рассмотрим общий метод нахождения оптимальных стратегий обоих игроков через решение двойственной пары задач линейного программирования.
Для второго игрока оптимальную смешанную стратегию даст решение двойственной задачи. При этом учтём, что оптимальная точка К для стратегии первого игрока является пересечением двух прямых МК и КТ, полученных из второго и третьего столбцов матрицы платежей. Тогда в оптимальной стратегии второго игрока возможности с этими номерами 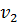 и
и 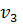 будут ненулевыми, а не участие первой прямой ТР говорит о нулевом значении
будут ненулевыми, а не участие первой прямой ТР говорит о нулевом значении 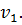
Тогда по аналогии с графическим методом нахождения оптимальной стратегии первого игрока найдём её и для второго игрока. Тоже построим горизонтальную ось с двумя точками на расстоянии 1, которым соответствуют чистые стратегии 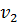 и
и 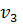 . На вертикальных осях отрезками соединим точки, полученные по строкам матрицы А во втором и третьем столбцах
. На вертикальных осях отрезками соединим точки, полученные по строкам матрицы А во втором и третьем столбцах 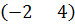 и
и 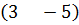 (см. Рисунок 5.б).
(см. Рисунок 5.б).
Для второго игрока находим область, точки которой лежат не ниже точек этих прямых. Границей такой области является ломаная NSW (нижняя граница выигрыша). Для этой области найдём точку с наименьшей ординатой – точку S. Она является пересечением двух прямых, что даёт систему уравнений
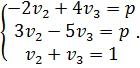
При этом 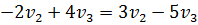 ,
, 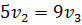 ,
, 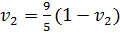 ,
, 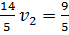 ,
, 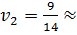 0.6429; Тогда
0.6429; Тогда 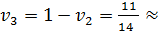 0.3571;
0.3571;  . При этом цена игры
. При этом цена игры 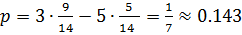 (как и было найдено ранее).
(как и было найдено ранее).
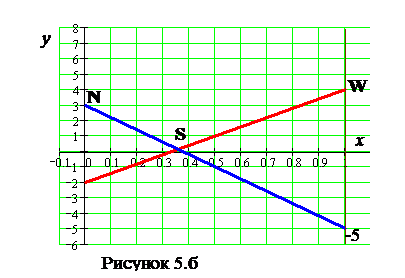
Получили, что для второго игрока в большой серии игр не следует применять первую возможность, вторую использовать в 64.29% и третью в 35.71% случаев.
д) Найдём оптимальные стратегии обоих игроков с решением двойственной пары задач линейного программирования (общий случай).
д.1) В матрице А имеются отрицательные значения, перейдём к матрице с неотрицательными элементами прибавляя к каждому элементу матрицы А число 6 (вычитая наименьший элемент в случае его отрицательности), получая новую матрицу 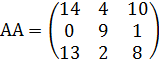 . Для этой игры будут прежние оптимальные стратегии игроков, а цена игры станет на 6 больше исходной;
. Для этой игры будут прежние оптимальные стратегии игроков, а цена игры станет на 6 больше исходной;
д.2) Для первого игрока (которому соответствуют строки матрицы АА) будем искать стратегию в виде 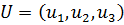 при условиях
при условиях 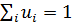 и
и 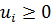 . Значение
. Значение 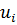 даёт вероятность (относительную частоту) применения возможности с номером
даёт вероятность (относительную частоту) применения возможности с номером 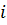 при большом числе игр.
при большом числе игр.
Для нахождения оптимальной смешанной стратегии первого игрока введём новые переменные 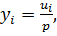
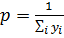 . Тогда получим первую задачу линейного программирования:
. Тогда получим первую задачу линейного программирования:
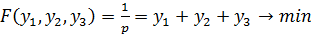
 (по столбцам таблицы АА).
(по столбцам таблицы АА).
На MathCADe составленная задача с учётом ранее заданной матрицы АА решается следующим образом:


д.3) Для второго игрока (которому соответствуют столбцы матрицы АА) будем искать стратегию в виде 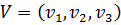 при условиях
при условиях 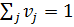 и
и 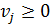 . Значение
. Значение 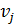 даёт вероятность (относительную частоту) применения возможности с номером
даёт вероятность (относительную частоту) применения возможности с номером 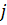 при большом числе игр.
при большом числе игр.
Для нахождения оптимальной смешанной стратегии первого игрока введём новые переменные 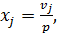
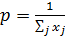 . Тогда получим вторую задачу линейного программирования, двойственную к первой:
. Тогда получим вторую задачу линейного программирования, двойственную к первой:
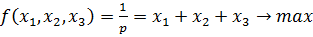
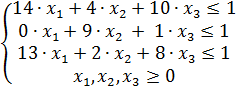 (по строкам таблицы АА).
(по строкам таблицы АА).
На MathCADe составленная задача с учётом ранее заданной матрицы АА решается следующим образом:

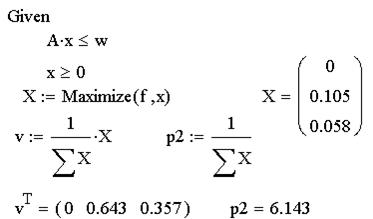
В обоих случаях получили цену игры 6.143, тогда для исходной игры цена игры будет на 6 меньше, т.е. станет равна 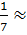 0.143.
0.143.
Ответ: для первого игрока оптимальная смешанная стратегия ( 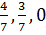 ), для второго игрока (0,
), для второго игрока (0, 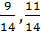 ) и цена игры равна
) и цена игры равна  .
.
Замечание 2: В следующей задаче рассмотрим метод разыгрывания игр по матрице платежей и стратегиям обоих игроков. Пользуясь им можно показать, что при найденных стратегиях обоих игроков средний выигрыш первого игрока действительно будет практически равен цене игры. Если первый игрок отклонится от своей оптимальной стратегии при оптимальной стратегии противника, то средний выигрыш первого игрока уменьшится; Если первый игрок станет придерживаться своей оптимальной стратегии, а противник отклонится от своей оптимальной стратегии, то средний выигрыш первого игрока при этом снизится.
№2.2 При истечении установленного срока для прибора он может оказаться в одном из трёх внешне неотличимых состояний (А,В,С). Управляющему нужно выполнить одно из трёх действий: I – выполнить только обычное плановое обслуживание, II – разборка и ремонт своими силами, III – замена на новый прибор. Дана матрица платежей (тыс.руб.) при выбранном действии в сочетании с состоянием прибора (при износе прибора получить скидку от производителя).
а) Выбрать оптимальную стратегию выборов действий для большого числа таких приборов;
б) Выбрать для одного выбора действие с минимальным ожидаемым ущербом при вероятностях трёх состояний 20%:50%:30% соответственно;
в) Выбрать единичное действие по критериям
в.1) Байеса при вероятностях состояний A,B,C 20%:50%:30% соответственно;
в.2) Вальда;
в.3) Гурвица при 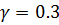 и
и 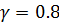 ;
;
в.4) Сэвиджа.
|
| А
| В
| С
|
| I
| 40
| 50
| 300
|
| II
| 80
| 30
| 50
|
| III
| 60
| 70
| 30
|
Решение:
а) Выбор оптимальной стратегии игрока при большом числе игр и нахождение цены игры.
а.1) Матрица игры
В данном случае для игрока с природой в заданной матрице указаны его затраты, что является выигрышем со знаком « - » и цель игрока –минимизация такого ущерба. Тогда первым игроком в привычном виде матричной игры является его противник – природа, хотя проигрыш игрока и не является её выигрышем. Тогда поменяем местами двух игроков для получения стандартного вида матричной игры, для этого матрицу платежей следует транспонировать без изменений знаков, получив 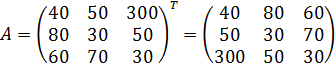 .
.
а.2) Проверим наличие седловой точки в матричной игре.
В первой строке минимальное значение 40, во второй 30 и в третьей 30. Тогда нижняя цена игры (максимин) 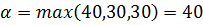 ;
;
В первом столбце максимальное значение 300, во втором 80 и в третьем 70. Тогда верхняя цена игры (минимакс) 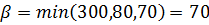 .
.
При 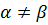 игра не имеет седловой точки, тогда оптимальные стратегии обоих игроков смешанные (содержат несколько возможностей);
игра не имеет седловой точки, тогда оптимальные стратегии обоих игроков смешанные (содержат несколько возможностей);
На MatCADe такую проверку при любых размерностях матрицы платежей можно выполнить так:

а.3) Оптимальная стратегия игрока и цена игры.
Для игрока (которому соответствуют столбцы матрицы А) будем искать смешанную стратегию в виде 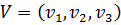 при условиях
при условиях 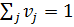 и
и 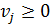 . Значение
. Значение 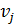 даёт вероятность (относительную частоту) применения возможности с номером
даёт вероятность (относительную частоту) применения возможности с номером 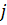 игрока при большом числе игр.
игрока при большом числе игр.
Для нахождения оптимальной смешанной стратегии первого игрока введём новые переменные 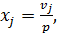
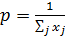 . Тогда получим первую задачу:
. Тогда получим первую задачу:
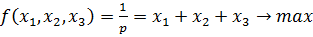
 (по столбцах исходной таблицы).
(по столбцах исходной таблицы).
На MathCADe составленная задача с учётом ранее заданной матрицы А решается следующим образом:
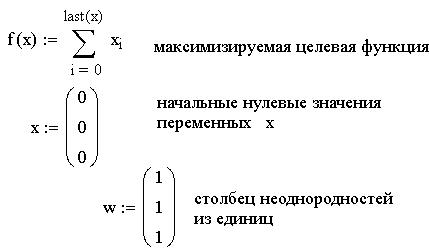

Получили, что в большой серии однотипных игр первый игрок заплатит в среднем по 61.264 руб. за игру при оптимальной стратегии противника и оптимальной своей стратегии, которая заключается в применении первой возможности в 10,3% случаев, второй возможности в 16,7% и 73% третьей возможности. Если противник (природа) применяет неоптимальную стратегию, то выигрыш игрока увеличится, т.е. его средний и общий платёж снизятся;
а.4) Оптимальная стратегия противника (природы) при большом числе игр.
Можно найти оптимальную стратегию для противника (природы), при которой платежи игрока при его оптимальной стратегии будут минимальными.
Для этого запишем вторую задачу линейного программирования, которая двойственна к составленной ранее задаче линейного программирования.
Для первого игрока (которому соответствуют строки матрицы А) будем искать стратегию в виде 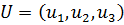 при условиях
при условиях 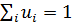 и
и 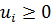 . Значение
. Значение 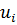 даёт вероятность (относительную частоту) применения возможности с номером
даёт вероятность (относительную частоту) применения возможности с номером 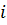 при большом числе игр.
при большом числе игр.
Для нахождения оптимальной смешанной стратегии первого игрока введём новые переменные 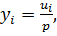
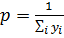 .
.
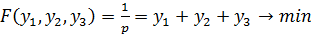
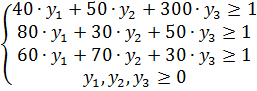 (по строкам исходной таблицы).
(по строкам исходной таблицы).
На MathCADe составленная задача с учётом ранее заданной матрицы А решается следующим образом:


После этого остаётся минимизировать заданную функцию F в окрестности заданного начального значения вектора v.


Получили, что наиболее неудачным для управляющего будут случаи , когда прибор после установленного срока принимает состояние А в 59,8%, состояние В в 33,3% и состояние С в 6,9% случаев. Если игрок (управляющий) будет использовать оптимальную стратегию выбора действий по обслуживанию приборов, то в среднем на один прибор затраты составят 61,264 руб.;
б) Разыгрывание серии игр с заданными стратегиями игроков.
Пусть по статистическим данным известно, что после установленного срока эксплуатации такой прибор принимает состояние А в 20%, состояние В в 50% и состояние С в 30% случаев. Это является стратегией противника 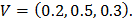
При большом числе игр можно на компьютере разыграть серию игр с выбранными стратегиями обоих игроков и матрицей платежей. Для этого составим функцию, которая по случайному числу и вектору смешанной стратегии даёт номер одной из её возможностей:
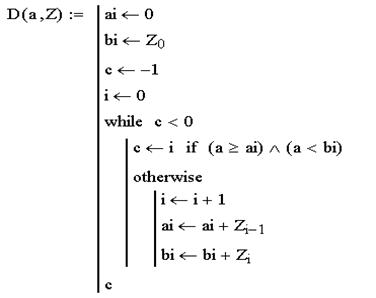
Именно так компьютер наудачу выбирает одну из нескольких возможностей, заданных программистом вместе с их вероятностями, по случайному числу. Например, случайный приз после прохождения уровня игры, рассчитывается именно так.
После этого создаётся цикл по количеству игр и на каждом шаге определяется выбор возможностей каждым игроком, по которым из матрицы платежей находим затраты на этом шаге.
 и т.д.
и т.д.
По последней составляющей массива Matr получим
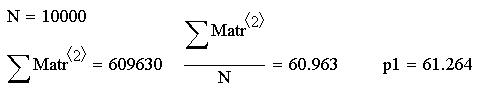
т.е. при неоптимальной стратегии U противника (природы) средние затраты игрока действительно снизились на 1.301 руб. в одной игре (действии с одним прибором). Чем сильнее отличие стратегии природы от оптимальной, тем заметнее снижение средних затрат игрока (но средний платёж не станет меньше нижней цены игры 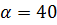 руб.).
руб.).
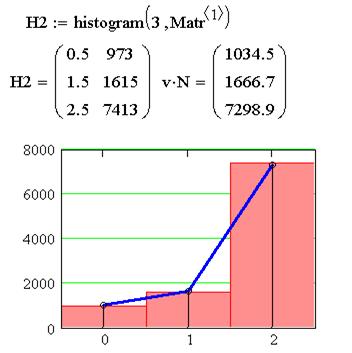 Составим распределение возможностей обоих игроков в этой серии игр и сравним их с теми, которые должны были бы быть при заданных их смешанных стратегиях:
Составим распределение возможностей обоих игроков в этой серии игр и сравним их с теми, которые должны были бы быть при заданных их смешанных стратегиях:
На Рисунке 6.а сравнение наблюдавшихся частот применения возможностей игрока и их частот при выбранной смешанной стратегии.
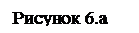 На первом рисунке гистограммой показаны реальные количества, а ломаная показывает их теоретические количества при выбранной стратегии (их отличия практически незаметны).
На первом рисунке гистограммой показаны реальные количества, а ломаная показывает их теоретические количества при выбранной стратегии (их отличия практически незаметны).
На Рисунке 6.б сравнение наблюдаемых частот применения природой возможностей при данной смешанной стратегии (закрашенные прямоугольники), теоретических частот при выбранной стратегии (ломаная линия) и частот при оптимальной стратегии (незакрашенные прямоугольники).
По обеим частям Рисунка 6 рисункам видно, что реальные количества не идеально соответствуют теоретическим, но их отличия несущественны.
По той же программе разыграем серию игр при оптимальных стратегиях обоих игроков, найденных ранее, в количестве N=10000:
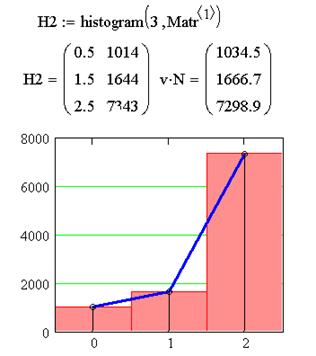
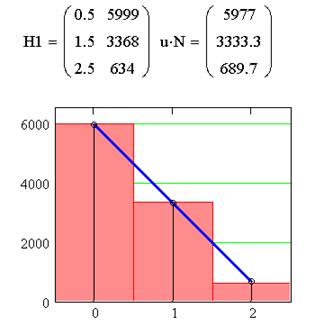
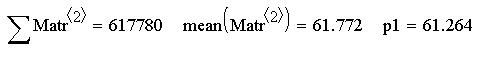
т.е. при практически оптимальных стратегиях обоих игроков с частотами применения на Рисунке 7 получили, что средний платёж (ущерб) в одной игре мало отличается от цены игры 61.264 руб (являясь чуть меньшим, что выгодно для игрока).
в) Критерии выбора одной из возможностей в одной игре.
|
| А
| В
| С
|
| I
| 40
| 50
| 300
|
| II
| 80
| 30
| 50
|
| III
| 60
| 70
| 30
|
Если предстоит только один выбор действия по данному прибору, то имеется несколько различных критериев такого выбора для второго игрока (который минимизирует проигрыш):
в.1) Критерий Байеса (по математическому ожиданию нанесённого ущерба):
Пусть известны вероятности 20%:50%:30% состояний природы, т.е. 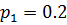 ,
, 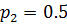 ,
, 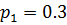 состояний А, В, С прибора.
состояний А, В, С прибора.
Если игрок выберет первую свою возможность I, то математическое ожидание для размера ущерба (платежей) составит 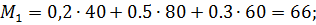
При выборе II он составит 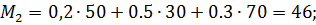
При выборе III он составит 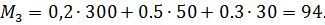
Тогда из учёта 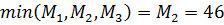 получим оптимальным выбор игроком возможности II – разборка и ремонт своими силами;
получим оптимальным выбор игроком возможности II – разборка и ремонт своими силами;
в.2) Критерий Лапласа (при равной вероятности состояний природы, принцип недостаточного основания):
Среди средних проигрышей берётся минимальный, считая 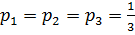
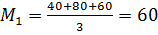 ,
,
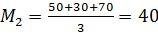 ,
,
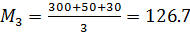 ,
,
тогда из учёта 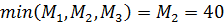 получим оптимальным выбор игроком возможности II – разборка и ремонт своими силами;
получим оптимальным выбор игроком возможности II – разборка и ремонт своими силами;
в.3) Критерий Вальда (минимаксный, пессимистический):
При выборе возможности I игрок максимально проиграет 300, при выборе II максимальный проигрыш 80, а при III он 70. Тогда выбираем возможность по правилу 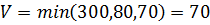 (
( 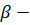 верхняя цена игры) при выборе возможности III.
верхняя цена игры) при выборе возможности III.
В противовес наиболее пессимистическому, имеется и наиболее оптимистический выбор: При выборе возможности I игрок минимально проиграет 40, при выборе II минимальный проигрыш 30, а при III он 30. Тогда выбираем возможность по правилу 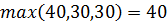 (
( 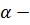 нижняя цена игры) при выборе возможности I.
нижняя цена игры) при выборе возможности I.
в.4) Критерий Гурвица зависит от параметра 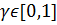 и состоит в вычислении значения
и состоит в вычислении значения 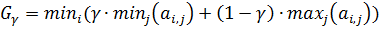 .
.
Значение  можно считать коэффициентом оптимизма: при
можно считать коэффициентом оптимизма: при 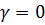 получим наиболее пессимистическое значение из критерия Вальда, при
получим наиболее пессимистическое значение из критерия Вальда, при 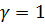 наиболее оптимистическое значение.
наиболее оптимистическое значение.
при 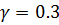 получим в первой строке
получим в первой строке 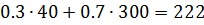 ,
,
| Критерий Гурвица
|
|
| 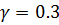
| 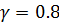
|
| I
| 222
| 92
|
| II
| 65
| 40
|
| III
| 58
| 38
|
во второй строке 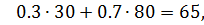
в третьей строке 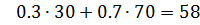 ;
;
при 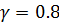 получим
получим
в первой строке 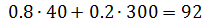 ,
,
во второй строке 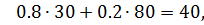
в третьей строке 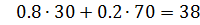 .
.
При 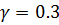
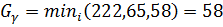 и возможность III,
и возможность III,
при 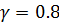
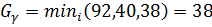 и возможность III.
и возможность III.
Таблица 4 Выбор одной возможности игрока по разным критериям
|
| Байеса
| Лапласа
| Вальда
| Гурвица
|
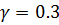
| 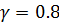
|
| I
|
|
|
|
|
|
| II
| х
| х
|
|
|
|
| III
|
|
| х
| х
| х
|
Ответ: При большом количестве принятий решений следует применять действие I в 10,3% случаев, действие II в 16,7% и III в 73% случаев. Тогда при наихудшем состоянии приборов в среднем затраты составят по 61.264 руб. При единственном решении рекомендации указаны в Таблице 4.
Замечание 4: В данной и аналогичной задачах игрок с природой выступил в виде второго игрока в стандартной постановке задачи на отыскание оптимальной стратегии. Если игроку соответствуют строки матрицы, в которой указаны его выигрыши с возможными знаками, то в критериях выбора строки и столбцы поменяются местами.
|
| П1
| П2
| П3
|
| К1
| -200
| 50
| 300
|
| К2
| 80
| 400
| -250
|
| К3
| 500
| -150
| 30
|
№2.3 (самостоятельно) Фермер может на участке посадить одну из трёх культур - К1, К2, К3. Ожидаемая прибыль от каждой культуры в зависимости от трёх видов погоды П1, П2, П3 будущим летом указаны в таблице. Найти оптимальную стратегию посадки а) на большом числе участков в разных районах с возможно различной погодой и ожидаемую прибыль при худшем наборе погодных условий;
б) на одном участке по критерию Гурвица при 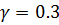 .
.
Ответ: а) К1-44.8%, К2-25.5%, К3-29.8% и цена игры 79.605 ден. при наихудшем варианте погодных условий П1-25.1%, П2-38.0%, П3-36.9%;
б) культура К3 при 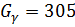 .
.
Задачи по теме «Графы».
Теоретическое вступление.
Графами можно представить ход выполнения большого числа процессов, процедур. Имеется большой класс задач оптимизации с применением графов и большое число алгоритмов их решения.
Рассмотрим ориентированный взвешенный граф G.
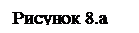
Кроме графического есть несколько других способов задания этого графа:
· Такой граф можно задать списком инцидентностей, где перечислены все его вершины с указанием начальной вершины (её номера), конечной вершины и веса этой дуги. Данный граф содержит 20 дуг, его список инцидентностей имеет вид:
| Номер
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
| 11
| 12
| 13
| 14
| 15
| 16
| 17
| 18
| 19
| 20
|
| Начало
| 0
| 0
| 0
| 1
| 2
| 2
| 2
| 2
| 3
| 3
| 3
| 4
| 5
| 5
| 5
| 6
| 6
| 7
| 8
| 9
|
| Конец
| 1
| 2
| 3
| 4
| 1
| 4
| 5
| 7
| 2
| 5
| 6
| 7
| 7
| 8
| 9
| 5
| 9
| 10
| 10
| 10
|
| Вес
| 1
| 4
| 2
| 5
| 3
| 1
| 3
| 2
| 1
| 6
| 3
| 2
| 3
| 6
| 2
| 2
| 5
| 8
| 1
| 2
|
· Можно задать его и матрицей смежностей – квадратной матрицей, где вершинам в обозначении строк указываются по этой строке смежные вершины в соответствующих столбцах с указанием веса ведущих в них дуг. Данный граф имеет 11 вершин (считая В= 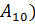 , его матрица смежностей имеет вид:
, его матрица смежностей имеет вид:
|
| 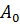
| 
| 
| 
| 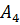
| 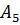
| 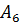
| 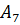
| 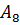
| 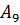
| 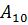
|
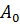
|
| 1
| 4
| 2
|
|
|
|
|
|
|
|

|
|
|
|
| 5
|
|
|
|
|
|
|

|
| 3
|
|
| 1
| 3
|
| 2
|
|
|
|

|
|
| 1
|
|
| 6
| 3
|
|
|
|
|
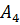
|
|
|
|
|
|
|
| 2
|
|
|
|
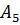
|
|
|
|
|
|
|
| 3
| 6
| 2
|
|
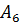
|
|
|
|
|
| 2
|
|
|
| 5
|
|
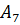
|
|
|
|
|
|
|
|
|
|
| 8
|
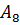
|
|
|
|
|
|
|
|
|
|
| 1
|
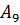
|
|
|
|
|
|
|
|
|
|
| 2
|
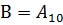
|
|
|
|
|
|
|
|
|
|
|
|
· Граф можно задать и некоторым бинарным отношением 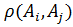 , при значении 1 для двух вершин графа в графе имеется дуга
, при значении 1 для двух вершин графа в графе имеется дуга 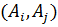 между этими вершинами, а при его значении 0 дуга отсутствует.
между этими вершинами, а при его значении 0 дуга отсутствует.
Между некоторыми вершинами графа G имеется дуга с указанным весом. В зависимости от смысла этих весов можно рассмотреть несколько различных задач оптимизации на графах. В большинстве случаев интересует наличие маршрута между двумя вершинами (достижимость из выбранной вершины другой вершины графа); При нескольких таких маршрутах иногда нужно найти имеющий минимальный либо максимальный общий вес; В некоторых случаях ищут маршрут с максимальной пропускной способностью. Рассмотрим эти задачи на одном графе с примерами реальных задач, которые к этому приводят.
В зависимости от решаемой задачи незаполненные клетки матрицы смежностей, говорящие об отсутствии дуги, заполняют по-разному: При отыскании маршрута с минимальным общим весом отсутствующей дуге присваивают очень большой вес М (бесконечно большой); При отыскании маршрута с максимальным общим весом отсутствующей дуге (при отсутствии реальных дуг с нулевым и с отрицательными весами) присваивают нулевой вес.
а) Маршрут с наименьшим общим весом.
В случае положительных весов для дуг графа они могут быть затратами (времени, бензина, длиной маршрута,…) и логично общий такой вес маршрута считать целевой функцией и её следует минимизировать. При этом должны выполняться несколько условий: в очередной вершине маршрута неважно, по какому пути попали в эту вершину; общая целевая функция аддитивна, т.е. получена суммой весов на участвующих в маршруте дуг.
Примерами таких задач могут бытьследующие:
Ø Граф описывает расстояния (или время движения) между парами населённых пунктов. Требуется найти маршрут из пункта А в пункт В с меньшим расстоянием (временем в пути);
Ø Из пункта А в пункт В ведёт сеть маршрутов с указанием тарифа перевозки по ним 1 т. груза. Найти маршрут, по которому перевозка 200 т. такого груза из А в В будет наиболее выгодна;
Ø Некоторый процесс разбит на операции, для которых взаимозаменяемые изображены в одной вертикали (не исключая отсутствие некоторых типов операций в некоторых допустимых способах выполнения процесса). Дуги указывают допустимые последовательности выполнения операций, их вес даёт время выполнения в сутках. Найти минимальное время выполнения всего процесса.
Алгоритм Форда-Беллмана решения такого типа задач:
1) Каждой из вершин присвоим числовое значение – условный вес 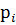 , который на начальном этапе берём равным очень большому числу М (например, здесь можно взять М=10000). Для начальной вершины условный вес задаём равным 0;
, который на начальном этапе берём равным очень большому числу М (например, здесь можно взять М=10000). Для начальной вершины условный вес задаём равным 0;
2) Для начальной вершиной А0 находим все смежные (по строке матрицы смежностей либо записи в матрице инцидентностей с начальной вершиной А0). Для каждой из них заменяем условный вес на число, равное весу соответствующей дуги в сумме с условным весом 0 начальной верш



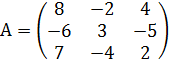 .
.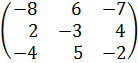 ;
;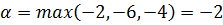 ;
;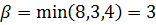 .
.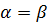 , то игра имела бы седловую точку и оптимальные стратегии обоих игроков были бы чистыми с постоянным выбором той возможности, где достигаются
, то игра имела бы седловую точку и оптимальные стратегии обоих игроков были бы чистыми с постоянным выбором той возможности, где достигаются 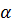 по строкам и
по строкам и 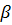 по столбцам. При этом обоим игрокам будет невыгодно отклоняться от этих оптимальных стратегий – при этом первый игрок может выиграть меньше и второй игрок может проиграть больше значения
по столбцам. При этом обоим игрокам будет невыгодно отклоняться от этих оптимальных стратегий – при этом первый игрок может выиграть меньше и второй игрок может проиграть больше значения 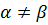 , тогда игра не имеет седловой точки, тогда оптимальные стратегии обоих игроков смешанные (содержат несколько возможностей). При этом цена игры, как средний платёж первого игрока при оптимальных стратегиях игроков в большом числе таких игр, будет между
, тогда игра не имеет седловой точки, тогда оптимальные стратегии обоих игроков смешанные (содержат несколько возможностей). При этом цена игры, как средний платёж первого игрока при оптимальных стратегиях игроков в большом числе таких игр, будет между 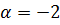 и
и 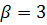 ;
;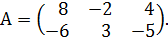
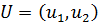 при условиях
при условиях 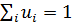 и
и 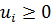 . Значение
. Значение 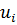 даёт вероятность (относительную частоту) применения возможности с номером
даёт вероятность (относительную частоту) применения возможности с номером 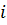 при большом числе игр.
при большом числе игр.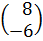 ,
, 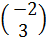 ,
, 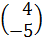 и такие точки попарно соединим прямыми линиями, см. Рисунок 3.а. Для первого игрока на построенном горизонтальном отрезке находим область, точки которой лежат не выше каждой из построенных прямых. Здесь верхней границей области будет ломаная МКТР (при большем числе столбцов матрицы А ломаная может быть более сложного вида).
и такие точки попарно соединим прямыми линиями, см. Рисунок 3.а. Для первого игрока на построенном горизонтальном отрезке находим область, точки которой лежат не выше каждой из построенных прямых. Здесь верхней границей области будет ломаная МКТР (при большем числе столбцов матрицы А ломаная может быть более сложного вида).
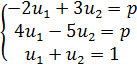
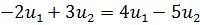 ,
,  ,
, 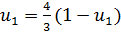 ,
, 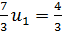 ,
, 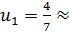 0.5714; Тогда
0.5714; Тогда 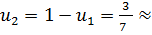 0.4286; В исходной задаче с тремя возможностями первого игрока
0.4286; В исходной задаче с тремя возможностями первого игрока 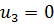 . При этом цена игры
. При этом цена игры 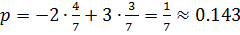 .
.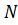 игр средний выигрыш будет практически равен
игр средний выигрыш будет практически равен 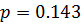 и его общий выигрыш станет около
и его общий выигрыш станет около 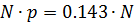 ден.ед.
ден.ед. 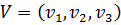 при условиях
при условиях 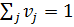 и
и 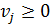 . Значение
. Значение 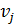 даёт вероятность (относительную частоту) применения возможности с номером
даёт вероятность (относительную частоту) применения возможности с номером 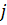 второго игрока при большом числе игр. В следующей пункте рассмотрим общий метод нахождения оптимальных стратегий обоих игроков через решение двойственной пары задач линейного программирования.
второго игрока при большом числе игр. В следующей пункте рассмотрим общий метод нахождения оптимальных стратегий обоих игроков через решение двойственной пары задач линейного программирования.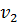 и
и 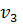 будут ненулевыми, а не участие первой прямой ТР говорит о нулевом значении
будут ненулевыми, а не участие первой прямой ТР говорит о нулевом значении 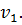
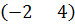 и
и 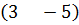 (см. Рисунок 5.б).
(см. Рисунок 5.б).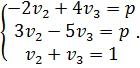
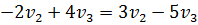 ,
, 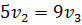 ,
, 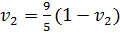 ,
, 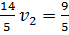 ,
, 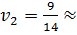 0.6429; Тогда
0.6429; Тогда 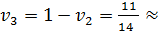 0.3571;
0.3571;  . При этом цена игры
. При этом цена игры 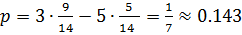 (как и было найдено ранее).
(как и было найдено ранее).
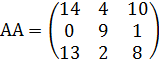 . Для этой игры будут прежние оптимальные стратегии игроков, а цена игры станет на 6 больше исходной;
. Для этой игры будут прежние оптимальные стратегии игроков, а цена игры станет на 6 больше исходной;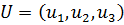 при условиях
при условиях 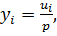
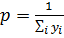 . Тогда получим первую задачу линейного программирования:
. Тогда получим первую задачу линейного программирования: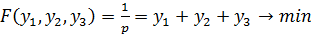
 (по столбцам таблицы АА).
(по столбцам таблицы АА).

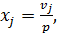
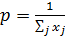 . Тогда получим вторую задачу линейного программирования, двойственную к первой:
. Тогда получим вторую задачу линейного программирования, двойственную к первой: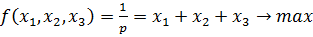
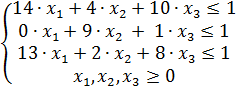 (по строкам таблицы АА).
(по строкам таблицы АА).
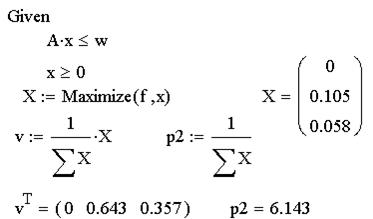
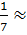 0.143.
0.143.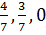 ), для второго игрока (0,
), для второго игрока (0, 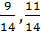 ) и цена игры равна
) и цена игры равна  .
.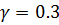 и
и 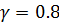 ;
;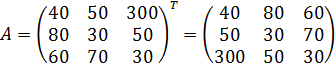 .
.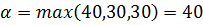 ;
;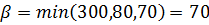 .
.
 (по столбцах исходной таблицы).
(по столбцах исходной таблицы).

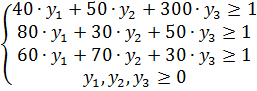 (по строкам исходной таблицы).
(по строкам исходной таблицы).



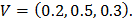
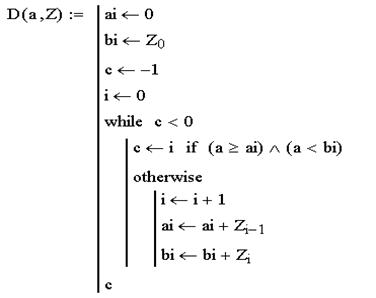
 и т.д.
и т.д.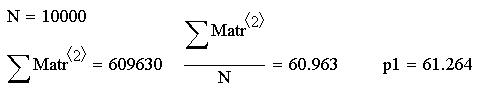
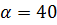 руб.).
руб.).  Составим распределение возможностей обоих игроков в этой серии игр и сравним их с теми, которые должны были бы быть при заданных их смешанных стратегиях:
Составим распределение возможностей обоих игроков в этой серии игр и сравним их с теми, которые должны были бы быть при заданных их смешанных стратегиях: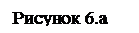 На первом рисунке гистограммой показаны реальные количества, а ломаная показывает их теоретические количества при выбранной стратегии (их отличия практически незаметны).
На первом рисунке гистограммой показаны реальные количества, а ломаная показывает их теоретические количества при выбранной стратегии (их отличия практически незаметны).
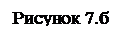


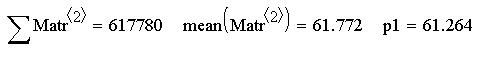
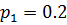 ,
, 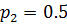 ,
, 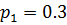 состояний А, В, С прибора.
состояний А, В, С прибора.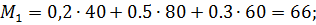
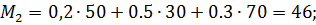
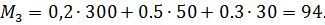
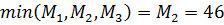 получим оптимальным выбор игроком возможности II – разборка и ремонт своими силами;
получим оптимальным выбор игроком возможности II – разборка и ремонт своими силами;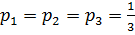
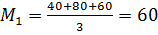 ,
,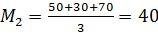 ,
,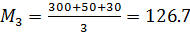 ,
,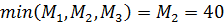 получим оптимальным выбор игроком возможности II – разборка и ремонт своими силами;
получим оптимальным выбор игроком возможности II – разборка и ремонт своими силами;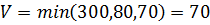 (
( 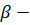 верхняя цена игры) при выборе возможности III.
верхняя цена игры) при выборе возможности III.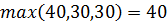 (
( 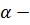 нижняя цена игры) при выборе возможности I.
нижняя цена игры) при выборе возможности I.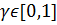 и состоит в вычислении значения
и состоит в вычислении значения 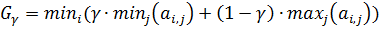 .
. можно считать коэффициентом оптимизма: при
можно считать коэффициентом оптимизма: при 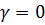 получим наиболее пессимистическое значение из критерия Вальда, при
получим наиболее пессимистическое значение из критерия Вальда, при 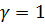 наиболее оптимистическое значение.
наиболее оптимистическое значение.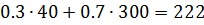 ,
, 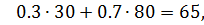
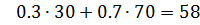 ;
;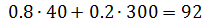 ,
, 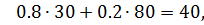
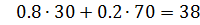 .
.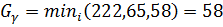 и возможность III,
и возможность III,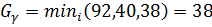 и возможность III.
и возможность III.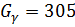 .
.

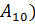 , его матрица смежностей имеет вид:
, его матрица смежностей имеет вид: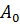



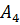
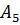
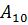
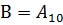
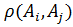 , при значении 1 для двух вершин графа в графе имеется дуга
, при значении 1 для двух вершин графа в графе имеется дуга 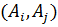 между этими вершинами, а при его значении 0 дуга отсутствует.
между этими вершинами, а при его значении 0 дуга отсутствует.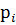 , который на начальном этапе берём равным очень большому числу М (например, здесь можно взять М=10000). Для начальной вершины условный вес задаём равным 0;
, который на начальном этапе берём равным очень большому числу М (например, здесь можно взять М=10000). Для начальной вершины условный вес задаём равным 0;


