

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...
Топ:
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Интересное:
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Метод Хаффмена
Общие положения
К. Шеннон и Р. Фано предложили в наиболее чистом виде конструкцию кода переменной длины. В этом коде у каждого символа своя длина кодовой последовательности, как в азбуке Морзе. Но в отличие от азбуки Морзе, где конец кодовой последовательности определяется "третьим символом" — паузой, здесь нужно побеспокоиться о том, как определять завершение кода отдельного символа. Предлагается такое ограничение на код: никакая кодовая последовательность не является началом другой кодовой последовательности. Это свойство называется свойством префикса, а код, обладающий таким свойством, называется префиксным кодом.
В предположении, что кодируемые символы появляются в тексте независимо нужно стремиться уменьшать среднее число битов на один символ, т.е. математическое ожидание длины кодовой комбинации случайно выбранного символа, которое равно
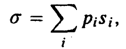
где pi — вероятность, а si — длина кодовой последовательности i -го символа.
Получается экстремальная задача.
Задача о префиксном коде. Минимизировать математическое ожидание 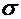 по всем наборам длин { si }, удовлетворяющим неравенству Крафта.
по всем наборам длин { si }, удовлетворяющим неравенству Крафта.
Теорема Крафта: Для того, чтобы набор целых чисел 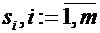 , мог быть набором длин путей поиска в схеме с
, мог быть набором длин путей поиска в схеме с 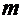 исходами, необходимо и достаточно, чтобы
исходами, необходимо и достаточно, чтобы
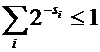 .
.
Набор, для которого 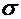 минимально, называется оптимальным. Шеннон и Фано предложили строить код, близкий к оптимальному, следующим способом: разбить все символы на две группы с приблизительно равными суммарными вероятностями, коды первой группы начать с 0, а второй группы — с 1; внутри каждой группы делать то же самое, пока в каждой группе не останется только по одному символу.
минимально, называется оптимальным. Шеннон и Фано предложили строить код, близкий к оптимальному, следующим способом: разбить все символы на две группы с приблизительно равными суммарными вероятностями, коды первой группы начать с 0, а второй группы — с 1; внутри каждой группы делать то же самое, пока в каждой группе не останется только по одному символу.
|
|
Элегантный алгоритм для точного решения этой задачи предложил Д. Хаффмен. Алгоритм основывается на нескольких очевидных свойствах оптимального набора {sj}.
Лемма 1. Пусть {р i} — набор вероятностей символов и {s i} — длины оптимальных кодовых комбинаций. Если p1 > р 2 >•••> рп, то s1 < s2 < ••• <sn.
Доказательство. Здесь достаточно сослаться на уже встречавшуюся нам задачу о перестановке, минимизирующей скалярное произведение двух векторов.
Задача о минимуме скалярного произведения Пусть заданы т чисел х1 х2,.., хm и еще т чисел у1, у2,..., ym. Составим пары (х, у), включив каждое х i, и каждое у j ровно в одну пару Затем перемножим числа каждой пары и сложим получившиеся произведения. Требуется найти такое разбиение чисел на пары, при котором значение получившейся суммы будет наименьшим.
Теорема. Наименьшее значение суммы попарных произведений достигается при сопоставлении возрастающей последовательности x, убывающей последовательности у.
Доказательство Покажем, что если найдутся две пары чисел 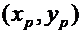 и
и 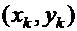 , такие что
, такие что 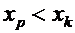 и
и 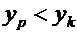 , то значение суммы попарных произведений можно уменьшить, заменив эти две пары парами
, то значение суммы попарных произведений можно уменьшить, заменив эти две пары парами 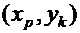 и
и 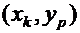 Действительно, так как
Действительно, так как
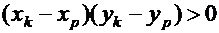 , то
, то
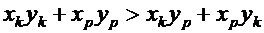 .
.
Поскольку число возможных расположении равно т!, т.е. конечное число, то начиная с любого расположения за конечное число шагов мы закончим процесс улучшений на расположении, которое дальше улучшить невозможно. На нем и достигается минимум.
Лемма 2. В обозначениях и предположении леммы 1 две самые длинные кодовые комбинации имеют одинаковую длину, т.е. 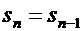 .
.
Доказательство. Действительно, пусть 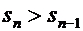 и, следовательно, п-я кодовая комбинация — самая длинная. Так как никакая кодовая комбинация не является началом никакой другой, то, сократив n-ю комбинацию до длины (n - 1)-й, мы получим снова уникальную кодовую комбинацию и более короткую, чем раньше, что невозможно для оптимальной кодировки.
и, следовательно, п-я кодовая комбинация — самая длинная. Так как никакая кодовая комбинация не является началом никакой другой, то, сократив n-ю комбинацию до длины (n - 1)-й, мы получим снова уникальную кодовую комбинацию и более короткую, чем раньше, что невозможно для оптимальной кодировки.
Лемма 3. Рассмотрим наравне с исходной задачей Р сокращенную задачу Р', которая получается объединением двух самых редких символов в один символ, — в предположении леммы 1 это два последних символа с суммарной вероятностью 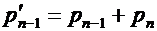 . Минимальное значение целевой функции в задаче Р' отличается от значения в задаче Р на
. Минимальное значение целевой функции в задаче Р' отличается от значения в задаче Р на 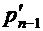 , а оптимальный кодовый набор для задачи Р получается из решения для задачи Р' удлинением на один бит кодовой последовательности для объединенного символа.
, а оптимальный кодовый набор для задачи Р получается из решения для задачи Р' удлинением на один бит кодовой последовательности для объединенного символа.
|
|
Доказательство. Действительно, каждому кодовому набору для задачи Р' можно так, как сказано в утверждении леммы, сопоставить кодовый набор для задачи Р с равными длинами самых редких символов. Это удлинение и приводит к приращению целевой функции на 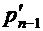 .
.
Теперь можно рассуждать так: в задаче Р мы ищем минимум на множестве кодов, которое мы обозначим через Сn , а в задаче Р' — аналогично на множестве Cn-1. В соответствии с леммой 2 в задаче Р можно искать минимум на множестве С' n, собственном подмножестве Сn , состоящем из таких наборов, в которых две самые длинные кодовые последовательности имеют одинаковую длину. Имеется взаимнооднозначное соответствие между Cn-1 и С' n, и значения целевых функций на соответствующих элементах двух множеств отличаются на постоянное слагаемое. Следовательно, и минимумы отличаются на это же постоянное слагаемое, так что минимуму в задаче Р' соответствует минимум на С' n, а он будет минимумом и для задачи Р.
Алгоритм, основанный на этих леммах, описывается в несколько строк: если в алфавите два символа, то нужно закодировать их 0 и 1, а если больше, то соединить два самых редких символа в один новый символ, решить получившуюся задачу и вновь разделить этот новый символ, приписав 0 и 1 к его кодовой последовательности.
|
|
|

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!