

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров...
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Интересное:
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
1.1. Основные определения.
Понятие множества принадлежит к числу фундаментальных неопределяемых понятий математики.
Множество — это любая определенная совокупность объектов.
Элементы - объекты, из которых составлено множество.
Элементы множества различны и отличимы друг от друга.
Если объект х является элементом множества М, то говорят, что х принадлежит М. Обозначение: х 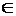 М. В противном случае говорят, что х не принадлежит М. Обозначение: х
М. В противном случае говорят, что х не принадлежит М. Обозначение: х 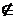 М.
М.
Существуют две проблемы в вопросах понятия элемента множества и его принадлежности
1) проблематична отличимость элементов. Например, символы о и а, которые встречаются на этой странице, — это один элемент множества А (в смысле они оба являются буквами) или два разных элемента (потому что это разные буквы)?
2) проблематична возможность (без дополнительных усилий) указать, принадлежит ли данный элемент данному множеству. Например, является ли число 86958476921537485067857467 простым?
Множества, как объекты, могут быть элементами других множеств.
Класс (семейство) множеств - множество, элементами которого являются множества.
Пустое множество – множество, не содержащее элементов. Обозначение: ø.
Обычно в конкретных рассуждениях элементы всех множеств берутся из некоторого одного, достаточно широкого множества U (своего для каждого случая), которое называется универсальным множеством (или универсумом).
Задание множеств
Существует три наиболее распространенных способа задания множеств:
1) перечисление элементов: 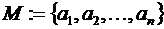 ;
;
2) характеристический предикат: 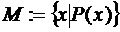 (это некоторое условие, выраженное в форме логического утверждения или процедуры, возвращающей логическое значение. Если для данного элемента условие выполнено, то он принадлежит определяемому множеству, в противном случае — не принадлежит)
(это некоторое условие, выраженное в форме логического утверждения или процедуры, возвращающей логическое значение. Если для данного элемента условие выполнено, то он принадлежит определяемому множеству, в противном случае — не принадлежит)
|
|
3) порождающая процедура: 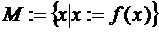 (это процедура, которая, будучи запущенной, порождает некоторые объекты, являющиеся элементами определяемого множества)
(это процедура, которая, будучи запущенной, порождает некоторые объекты, являющиеся элементами определяемого множества)
Пример: Требуется задать множество натуральных чисел от 10 до 17.
1. М: ={10,11,12,13,14,15,16,17};
2. M:={ 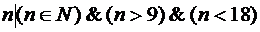 };
};
3. M: = { 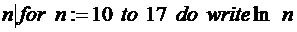 }.
}.
Перечислением можно задавать только конечные множества. Бесконечные множества задаются характеристическим предикатом или порождающей процедурой.
Пример:
N: = { n | n: = 0; while true do begin n: = n + 1; writeln n; endwhile }.
Парадокс Рассела: Пусть Y - множество всех множеств, не содержащих себя в качестве элемента, т.е. 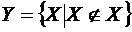 . Тогда невозможно ответить на вопрос о принадлежности
. Тогда невозможно ответить на вопрос о принадлежности 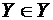 .
.
Доказательство: Пусть Y 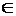 Y, но это означает, что Y содержит само себя, а по условию Y - множество всех множеств, не содержащих себя в качестве элемента, т.е. Y
Y, но это означает, что Y содержит само себя, а по условию Y - множество всех множеств, не содержащих себя в качестве элемента, т.е. Y 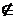 Y. Пусть Y
Y. Пусть Y 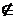 Y, тогда Y
Y, тогда Y 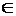 Y по условию, т.к. не содержит себя. Получается неустранимое логическое противоречие, которое известно как парадокс Рассела.
Y по условию, т.к. не содержит себя. Получается неустранимое логическое противоречие, которое известно как парадокс Рассела.
Данный парадокс известен также как парадокс брадобрея (или цирюльника) и будет рассмотрен в разделе парадоксов исчисления высказываний.
Операции над множествами
Множество А содержится в множестве В (множество В включает множество А), если каждый элемент А есть элемент В:
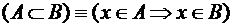 .
.
В этом случае А называется подмножеством В, В — надмножеством А.
Множество А называется собственным подмножеством множества В, если 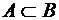 и
и 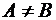 .
.
Если множество 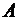 не является собственным подмножеством множества
не является собственным подмножеством множества 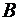 , имеет место следующее обозначение:
, имеет место следующее обозначение: 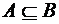 (
(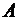 является подмножеством
является подмножеством 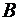 и может быть совпадающим с ним).
и может быть совпадающим с ним).
Каково бы ни было множество 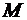 выполняются следующие два свойства:
выполняются следующие два свойства:
1) 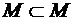 ;
;
2) ø 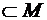
Два множества равны, если они являются подмножествами друг друга:
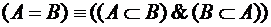 .
.
Мощность множества М обозначается как |М|. Для конечных множеств мощность — это число элементов. Например, | ø | = 0, но |{ ø }| == 1. Если  , то множества
, то множества 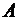 и
и 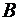 называются равномощными.
называются равномощными.
|
|
Каковы бы ни были два множества 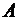 и
и 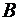 между ними возможны следующие операции:
между ними возможны следующие операции:
1. Пересечение. 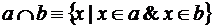
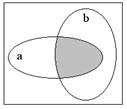
2. Объединение. 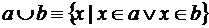
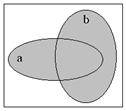
3. Разность. 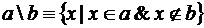
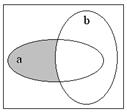
4. Дополнение (отрицание). 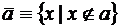
Операция дополнения подразумевает некоторый универсум (универсальное множество) 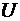 :
: 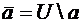 .
.
5. Симметрическая разность
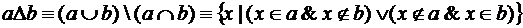
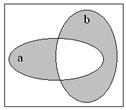
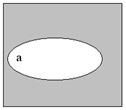
Здесь помимо самих операций приведены диаграммы Эйлера (в некоторой литературе[1] принято название Эйлера-Вена), иллюстрирующие операции над множествами. Сами исходные множества изображаются фигурами (в данном случае овалами), а результат графически выделяется (в данном случае для выделения использована штриховка).
Разбиения и покрытия
Пусть 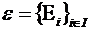 — некоторое семейство подмножеств множества
— некоторое семейство подмножеств множества 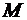 ,
, 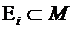 .
.
Семейство 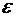 называется покрытием множества
называется покрытием множества 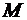 , если каждый элемент
, если каждый элемент 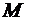 принадлежит хотя бы одному из
принадлежит хотя бы одному из 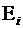 .
.
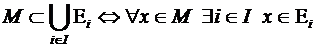 .
.
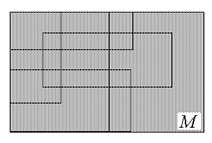
Семейство 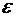 называется дизъюнктным, если элементы этого семейства попарно не пересекаются, то есть каждый элемент множества М принадлежит не более чем одному из множеств
называется дизъюнктным, если элементы этого семейства попарно не пересекаются, то есть каждый элемент множества М принадлежит не более чем одному из множеств 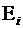 :
:
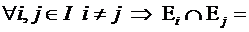 ø.
ø.
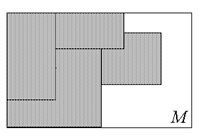
Дизъюнктное покрытие 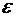 называется разбиением множества М.
называется разбиением множества М.
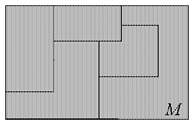
Пример
Пусть М: ={1,2,3}. Тогда {{1,2}, {2,3}, {3,1}} является покрытием, но не разбиением; {{1}, {2}, {3}} является разбиением (и покрытием), а семейство {{1}, {2}} является дизъюнктным, но не является ни покрытием, ни разбиением.
Булеан - множество всех подмножеств множества М: 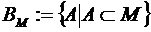 .
.
Теорема о булеане: Для любого конечного множества 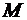 выполняется
выполняется
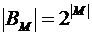 .
.
Доказательство:
База индукции: пусть М = ø, тогда 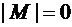 и
и 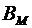 = {ø}. Поскольку
= {ø}. Поскольку 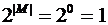 и
и 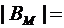 |{ ø }|
|{ ø }| 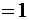 то условие теоремы выполняется.
то условие теоремы выполняется.
Индукционный переход: пусть условие теоремы выполняется для 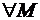 ,
, 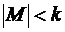 , т.е.
, т.е. 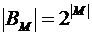 . Рассмотрим множество, мера которого
. Рассмотрим множество, мера которого 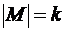 и
и 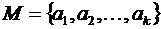 . Поскольку последний добавленный элемент
. Поскольку последний добавленный элемент 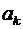 входит не во все подмножества из рассматриваемого булеана, введем следующие обозначения:
входит не во все подмножества из рассматриваемого булеана, введем следующие обозначения:
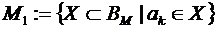 и
и 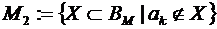 .
.
При этом 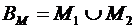 и
и 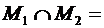 ø. По индукционному предположению
ø. По индукционному предположению 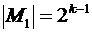 и
и 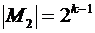 . Следовательно,
. Следовательно,
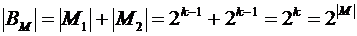 .
.
Теорема доказана.
Пересечение, объединение и разность подмножеств множества U (универсума) являются подмножествами множества U. Множество всех подмножеств множества U с операциями пересечения, объединения, разности и дополнения образует алгебру подмножеств множества U.
|
|
|

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!