Любая функция 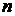 переменных
переменных  , полученная путем суперпозиции перечисленных элементарных булевых функций, также является булевой функцией, определенной на множестве наборов переменных
, полученная путем суперпозиции перечисленных элементарных булевых функций, также является булевой функцией, определенной на множестве наборов переменных 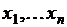 . Таблица истинности в данном случае будет иметь следующий вид:
. Таблица истинности в данном случае будет иметь следующий вид:
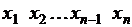
| 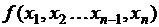
|
| 0 0.…..0 0
0 0.…..0 1
0 0.…..1 1
…………………
1 1.…..1 1
| 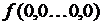
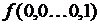
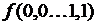 ………………
………………
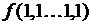
|
На основании теоремы о булеане, данная таблица будет иметь 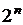 строк (т.к. мера множества переменных
строк (т.к. мера множества переменных 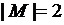 ), т.е. число всех наборов от
), т.е. число всех наборов от 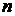 переменных равно
переменных равно 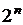 , а число всевозможных булевых функций, зависящих от
, а число всевозможных булевых функций, зависящих от 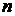 переменных равно
переменных равно 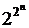 на основании той же теоремы.
на основании той же теоремы.
Два набора 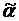 и
и 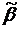 называются соседними по
называются соседними по 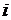 -ой компоненте, если они различимы только по значению переменной
-ой компоненте, если они различимы только по значению переменной 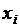 , т.е.
, т.е.
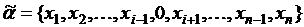 ,
,
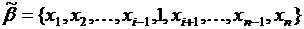 .
.
Набор 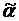 называется предшествующим к набору
называется предшествующим к набору 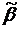 и обозначается
и обозначается 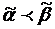 , если выполняется неравенство
, если выполняется неравенство  при всех значениях
при всех значениях  .
.
Переменная 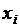 называется существенной, если на наборах, соседних по
называется существенной, если на наборах, соседних по 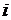 -ой компоненте, функция
-ой компоненте, функция  принимает различные значения, в противном случае переменная является фиктивной.
принимает различные значения, в противном случае переменная является фиктивной.
Замечание. Обнаружить фиктивные переменные некоторой функции можно не только по таблице истинности, но и аналитически: после всех элементарных преобразований функция  содержит только существенные переменные.
содержит только существенные переменные.
Пример: 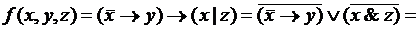
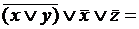
 ,
,
следовательно, переменная  является фиктивной, а
является фиктивной, а 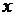 и
и 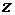 - существенными.
- существенными.
Функции  и
и 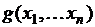 называются равными, если они могут быть получены одна из другой путем добавления или исключения фиктивных переменных.
называются равными, если они могут быть получены одна из другой путем добавления или исключения фиктивных переменных.
Функция  называется монотонной, если для любых двух наборов
называется монотонной, если для любых двух наборов 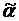 и
и 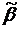 , таких что
, таких что 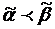 выполняется
выполняется 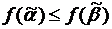 .
.
Теорема [2]: Какова бы ни была булева функция  , она может быть представлена в следующем виде:
, она может быть представлена в следующем виде:
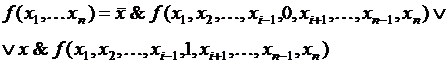
и данное представление называется разложением функции по 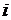 -ой компоненте.
-ой компоненте.
Рассмотрим функцию трех переменных 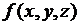 и разложим ее последовательно по всем переменным:
и разложим ее последовательно по всем переменным:
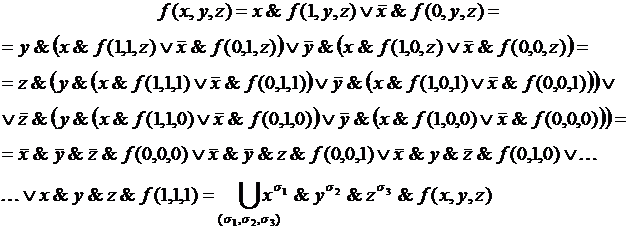 где дизъюнкция берется по всем возможным наборам переменных
где дизъюнкция берется по всем возможным наборам переменных 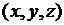 . Аналогичное разложение может быть получено для большего числа переменных.
. Аналогичное разложение может быть получено для большего числа переменных.
Приведенное разложение называется совершенной дизъюнктивной нормальной формой (СДНФ).
Данная форма называется совершенной, потому что каждое слагаемое в дизъюнкции включает все переменные, дизъюнктивной, потому что главная операция – дизъюнкция и нормальной, т.к. существует алгоритм проверки равносильности. При этом
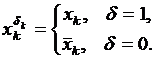
Иными словами, для того, чтобы построить СДНФ, необходимо в таблице истинности рассмотреть те наборы, на которых функция равна 1 и навесить отрицания на те переменные, которые на данных наборах равны 0 (т.к. все остальные слагаемые будут равны 0 по тождеству 9).
Если в данном разложении учесть двойственность дизъюнкции и конъюнкции (см. ранее) и заменить все дизъюнкции на конъюнкции, а конъюнкции – на дизъюнкции, получаем следующее представление, имеющее название СКНФ (совершенная конъюнктивная нормальная форма):
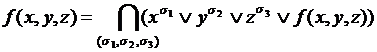
Иными словами, для того, чтобы построить СДНФ, необходимо в таблице истинности рассмотреть те наборы, на которых функция равна 0 и навесить отрицания на те переменные, которые на данных наборах равны 1 (т.к. все остальные сомножители будут равны 1 по тождеству 5).
Если в разложении булевой функции 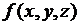 заменить все дизъюнкции на функцию
заменить все дизъюнкции на функцию 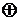 и учесть тождество 12
и учесть тождество 12 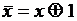 , получаем следующее представление, имеющее название СПНФ [3] (совершенная полиномиальная нормальная форма) или полином Жигалкина [4]:
, получаем следующее представление, имеющее название СПНФ [3] (совершенная полиномиальная нормальная форма) или полином Жигалкина [4]:
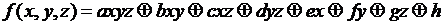 ,
,
где a,b,c,…,h – некоторые коэффициенты, которые могут быть найдены по таблице истинности.
СПНФ может быть также построена методом навешивания двойного отрицания. Основное необходимое тождество в данном случае - 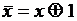 .
.
Пример:  .
.
Функция 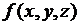 называется линейной, если в ее разложении в СПНФ отсутствуют конъюнкции.
называется линейной, если в ее разложении в СПНФ отсутствуют конъюнкции.
Теорема: Какова бы ни была булева функция  , она может быть выражена через функции
, она может быть выражена через функции 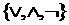 , которые являются базисом.
, которые являются базисом.
Доказательство: Если функция 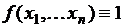 , то она может быть представлена в следующем виде:
, то она может быть представлена в следующем виде: 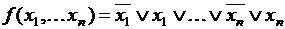 .
.
Если функция 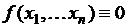 , то она может быть представлена в следующем виде:
, то она может быть представлена в следующем виде: 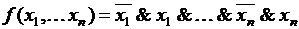 . В противном случае функция
. В противном случае функция  может быть представлена в виде СДНФ.
может быть представлена в виде СДНФ.
Теорема доказана.



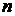 переменных
переменных  , полученная путем суперпозиции перечисленных элементарных булевых функций, также является булевой функцией, определенной на множестве наборов переменных
, полученная путем суперпозиции перечисленных элементарных булевых функций, также является булевой функцией, определенной на множестве наборов переменных 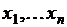 . Таблица истинности в данном случае будет иметь следующий вид:
. Таблица истинности в данном случае будет иметь следующий вид: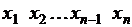
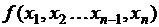
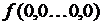
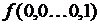
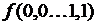 ………………
………………
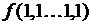
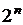 строк (т.к. мера множества переменных
строк (т.к. мера множества переменных 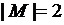 ), т.е. число всех наборов от
), т.е. число всех наборов от 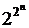 на основании той же теоремы.
на основании той же теоремы.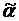 и
и 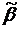 называются соседними по
называются соседними по 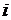 -ой компоненте, если они различимы только по значению переменной
-ой компоненте, если они различимы только по значению переменной 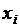 , т.е.
, т.е.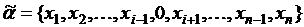 ,
,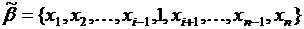 .
.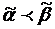 , если выполняется неравенство
, если выполняется неравенство  при всех значениях
при всех значениях  .
.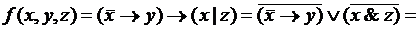
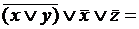
 ,
, является фиктивной, а
является фиктивной, а 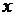 и
и 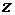 - существенными.
- существенными.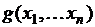 называются равными, если они могут быть получены одна из другой путем добавления или исключения фиктивных переменных.
называются равными, если они могут быть получены одна из другой путем добавления или исключения фиктивных переменных.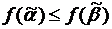 .
.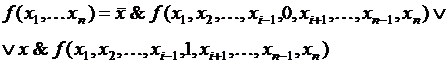
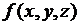 и разложим ее последовательно по всем переменным:
и разложим ее последовательно по всем переменным: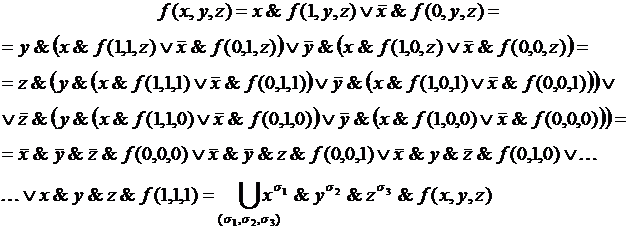 где дизъюнкция берется по всем возможным наборам переменных
где дизъюнкция берется по всем возможным наборам переменных 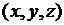 . Аналогичное разложение может быть получено для большего числа переменных.
. Аналогичное разложение может быть получено для большего числа переменных.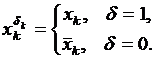
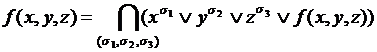
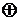 и учесть тождество 12
и учесть тождество 12 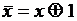 , получаем следующее представление, имеющее название СПНФ [3] (совершенная полиномиальная нормальная форма) или полином Жигалкина [4]:
, получаем следующее представление, имеющее название СПНФ [3] (совершенная полиномиальная нормальная форма) или полином Жигалкина [4]: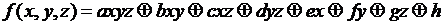 ,
, .
.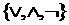 , которые являются базисом.
, которые являются базисом.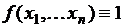 , то она может быть представлена в следующем виде:
, то она может быть представлена в следующем виде: 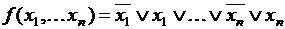 .
.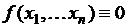 , то она может быть представлена в следующем виде:
, то она может быть представлена в следующем виде: 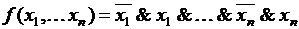 . В противном случае функция
. В противном случае функция 


