I. ОСНОВНЫЕ ПОНЯТИЯ.
II. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
Уравнение поперечных колебаний струны.
Физическая интерпретация
А). Распространение волны отклонения
При нулевой начальной скорости 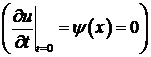 из формулы Даламбера получаем
из формулы Даламбера получаем
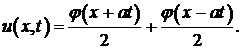
В этом случае колебания представляют собой процесс распространения начального отклонения 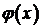 .
.
Функция вида 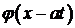 в физике называется распространяющейся волной – неизменный профиль
в физике называется распространяющейся волной – неизменный профиль 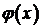 перемещается вправо со скоростью
перемещается вправо со скоростью  . Аналогично функция
. Аналогично функция 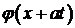 представляет неизменный профиль
представляет неизменный профиль 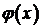 , перемещающийся влево со скоростью
, перемещающийся влево со скоростью  .
.
Значит, решение 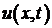 представляет собой сумму двух полуволн: прямой, бегущей вправо со скоростью
представляет собой сумму двух полуволн: прямой, бегущей вправо со скоростью  , и обратной, бегущей влево с той же скоростью. При этом начальная форма обеих волн определяется функцией
, и обратной, бегущей влево с той же скоростью. При этом начальная форма обеих волн определяется функцией 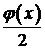 – половиной начального отклонения
– половиной начального отклонения 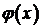 .
.
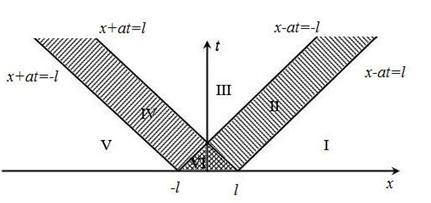 Рассмотрим фазовую плоскость
Рассмотрим фазовую плоскость  .
.
Линии 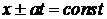 суть характеристики. Функция
суть характеристики. Функция 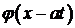 сохраняет постоянное значение на характеристиках
сохраняет постоянное значение на характеристиках 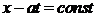 , а функция
, а функция 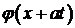 – на характеристиках
– на характеристиках 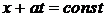 .
.
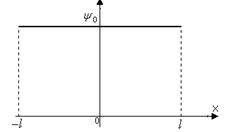
Предположим, что начальное отклонение отлично от нуля только в промежутке 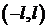 , а вне этого промежутка равно нулю.
, а вне этого промежутка равно нулю.
Характеристики 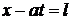 и
и 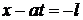 представляют собой передний и задний фронты прямой волны, а характеристики
представляют собой передний и задний фронты прямой волны, а характеристики 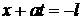 и
и 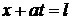 – соответственно передний и задний фронты обратной волны. Эти характеристики разбивают фазовую плоскость на несколько областей. Через область
– соответственно передний и задний фронты обратной волны. Эти характеристики разбивают фазовую плоскость на несколько областей. Через область 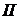
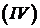 проходит прямая (обратная) волна, а в области
проходит прямая (обратная) волна, а в области 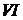 взаимодействуют обе волны. В область
взаимодействуют обе волны. В область 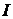 (и
(и 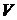 ) до некоторого момента времени
) до некоторого момента времени 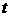 еще не дошла прямая (обратная) волна; через область
еще не дошла прямая (обратная) волна; через область  с некоторого момента
с некоторого момента 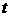 волны уже прошли и наступил покой.
волны уже прошли и наступил покой.
Б). Распространение волны импульса
При нулевом начальном отклонении 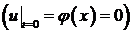 колебания вызываются начальной скоростью (или импульсом)
колебания вызываются начальной скоростью (или импульсом) 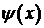 и решение задачи Коши можно представить в виде разности обратной и прямой волны:
и решение задачи Коши можно представить в виде разности обратной и прямой волны:
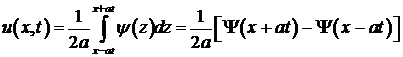
Здесь 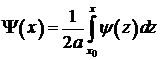 – первообразная функции
– первообразная функции  .
.
Например, пусть  и
и 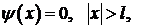 тогда
тогда
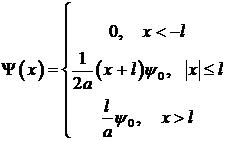
Графики функций 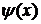 и
и 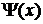 приведены на рисунке.
приведены на рисунке.
Начальный импульс 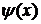 Функция
Функция 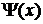 – профиль волны
– профиль волны
Полуограниченная и ограниченная струна.
Метод продолжения.
Задача о распространении волн на полуограниченной прямой 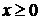 важна при изучении процесса отражения волны от края. Рассмотрим, например, задачу о распространении начального возмущения в струне с закрепленным краем.
важна при изучении процесса отражения волны от края. Рассмотрим, например, задачу о распространении начального возмущения в струне с закрепленным краем.
Найдем решение уравнения колебаний
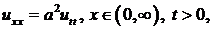
удовлетворяющее начальным условиям

и одному из граничных условий  (или
(или 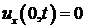 ).
).
Непосредственно воспользоваться формулой Даламбера мы не имеем права, т.к. заданные начальные функции 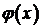 и
и 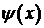 определены только на полупрямой
определены только на полупрямой 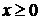 . Для возможности применения решения Даламбера следует продолжить начальные данные влево от
. Для возможности применения решения Даламбера следует продолжить начальные данные влево от  . С физической точки зрения это означает, что мы хотим задать такое начальное возмущение бесконечной струны, чтобы колебания ее участка
. С физической точки зрения это означает, что мы хотим задать такое начальное возмущение бесконечной струны, чтобы колебания ее участка 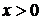 были такими же, как если бы конец
были такими же, как если бы конец  был закреплен (или свободен).
был закреплен (или свободен).
В случае закрепления конца  (граничное условие
(граничное условие  ) начальные данные следует продолжить на всю прямую нечетным образом. Тогда из формулы Даламбера при
) начальные данные следует продолжить на всю прямую нечетным образом. Тогда из формулы Даламбера при  получается
получается
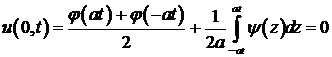
в силу нечетности функций  и
и  .
.
В случае свободного конца (граничное условие 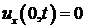 ) начальные данные следует продолжить на всю прямую четным образом.
) начальные данные следует продолжить на всю прямую четным образом.
Тогда из формулы Даламбера при  получаем
получаем

так как производная 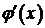 от четной функции является нечетной.
от четной функции является нечетной.
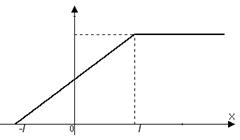
 Например, пусть в задаче для полубесконечной струны с закрепленным краем начальное отклонение отлично от нуля только в промежутке
Например, пусть в задаче для полубесконечной струны с закрепленным краем начальное отклонение отлично от нуля только в промежутке 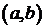 и имеет форму треугольника; начальная скорость равна нулю. Строим нечетное продолжение начального отклонения и смотрим, что происходит на фазовой плоскости (нас интересует реальная струна, то есть область
и имеет форму треугольника; начальная скорость равна нулю. Строим нечетное продолжение начального отклонения и смотрим, что происходит на фазовой плоскости (нас интересует реальная струна, то есть область 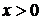 ). На рисунке совмещены фазовая плоскость
). На рисунке совмещены фазовая плоскость  и плоскость
и плоскость 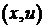 . В заштрихованных полосах отклонение отлично от нуля. Знаки плюс и минус указывают на знак фазы отклонения.
. В заштрихованных полосах отклонение отлично от нуля. Знаки плюс и минус указывают на знак фазы отклонения.
Здесь область  – процесс отражения обратной волны от закрепленного края, область
– процесс отражения обратной волны от закрепленного края, область  – отраженная волна (в противофазе).
– отраженная волна (в противофазе).
Чтобы воспользоваться формулой Даламбера для ограниченной струны 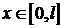 , продолжаем начальные данные для закрепленных концов нечетным образом влево от
, продолжаем начальные данные для закрепленных концов нечетным образом влево от  и вправо от
и вправо от 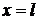 . Для свободных концов продолжаем начальные данные четным образом.
. Для свободных концов продолжаем начальные данные четным образом.
Задачи для самостоятельного решения
I. Решить следующие уравнения:
1)  . Ответ:
. Ответ: 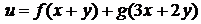 .
.
2) 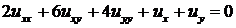 . Ответ:
. Ответ: 
3) 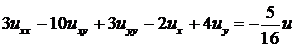 . Ответ:
. Ответ: 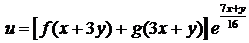 .
.
4)  . Ответ:
. Ответ: 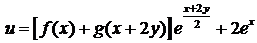 .
.
5) 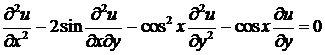 .
.
Ответ:  .
.
6)  . Ответ:
. Ответ: 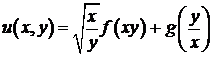 .
.
7) 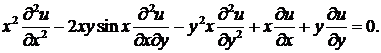
Ответ: 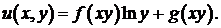
II. Пользуясь формулой Даламбера, решить задачи:
1) 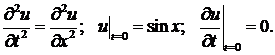
Ответ: 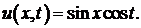
2) 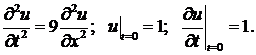
Ответ: 
III. Решить задачу Коши (найти решение уравнения, удовлетворяющее заданным начальным условиям
1)  ,
,
 .
.
Ответ: 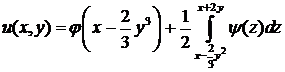 .
.
2)  .
.
Ответ:  .
.
3) 
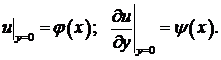
Ответ: 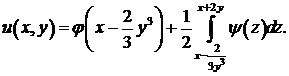
4) 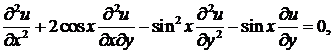
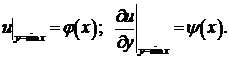
Ответ:  .
.
IV. Применить метод распространяющихся волн для решения задач.
1) Колебания бесконечной струны вызваны начальным отклонением

Начальная скорость и внешняя возмущающая сила равны нулю. Построить профиль струны в момент времени  На фазовой плоскости проследить за процессом при изменении
На фазовой плоскости проследить за процессом при изменении 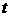 от 0 до
от 0 до 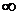 (вдоль вертикали) и при изменении
(вдоль вертикали) и при изменении 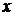 от
от 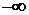 до
до  (вдоль горизонтали).
(вдоль горизонтали).
 2) Бесконечной струне на отрезке
2) Бесконечной струне на отрезке 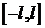 сообщена поперечная начальная скорость
сообщена поперечная начальная скорость 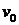 , вне этого отрезка начальная скорость равна нулю. Построить профиль струны для моментов времени
, вне этого отрезка начальная скорость равна нулю. Построить профиль струны для моментов времени 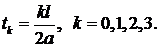
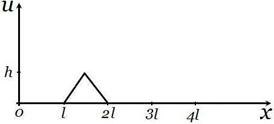
3) Полубесконечная струна, закрепленная в конце  , возмущена начальным отклонением (см. рис.). Построить профиль струны для моментов времени
, возмущена начальным отклонением (см. рис.). Построить профиль струны для моментов времени 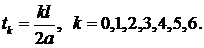 На фазовой плоскости проследить за процессом.
На фазовой плоскости проследить за процессом.
 4) Конечная струна, закрепленная на концах
4) Конечная струна, закрепленная на концах  ,
, 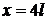 , возмущена начальным отклонением (см. рис.). Построить профиль струны для моментов времени
, возмущена начальным отклонением (см. рис.). Построить профиль струны для моментов времени 
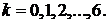 На фазовой плоскости проследить за процессом.
На фазовой плоскости проследить за процессом.
Задача Штурма – Лиувилля
А). Постановка задачи
Применение метода Фурье к решению задач математической физики (уравнений любого из трех типов) приводит к краевым задачам для обыкновенного линейного дифференциального однородного уравнения второго порядка, содержащего параметр. С нулевыми граничными условиями такие задачи, как правило, при любом значении параметра имеют тождественно равное нулю решение. Но при некоторых значениях параметра возможны и нетривиальные решения. В этих задачах требуется найти такие значения параметра, при которых существует отличное от нуля решение однородного уравнения, удовлетворяющее на концах отрезка однородным граничным условиям.
Сформулируем задачу Штурма-Лиувилля (Ш. – Л.):
Найти значения параметра  при которых уравнение
при которых уравнение
 (1)
(1)
имеет нетривиальные решения 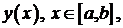 удовлетворяющие однородным краевым условиям
удовлетворяющие однородным краевым условиям
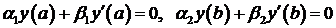 , (2)
, (2)
и найти эти решения.
Б). Нахождение собственных значений и собственных функций.
Пусть выполнены условия регулярности: 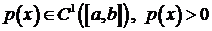 при
при 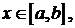
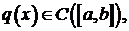

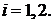 Предполагается, что решение задачи
Предполагается, что решение задачи 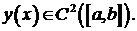 Значение параметра
Значение параметра  при котором существует нетривиальное решение задачи Ш. – Л., называется собственным значением, а соответствующее нетривиальное решение
при котором существует нетривиальное решение задачи Ш. – Л., называется собственным значением, а соответствующее нетривиальное решение 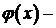 собственной функцией.
собственной функцией.
При сделанных предположениях существует фундаментальная система решений 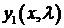 ,
, 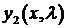 уравнения (1). Общее решение этого уравнения имеет вид
уравнения (1). Общее решение этого уравнения имеет вид
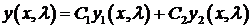 (3)
(3)
Здесь  – произвольные постоянные. Так как нас интересуют только нетривиальные решения, то должно быть
– произвольные постоянные. Так как нас интересуют только нетривиальные решения, то должно быть 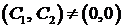 .
.
Подставим функцию (3) в краевые условия (2):
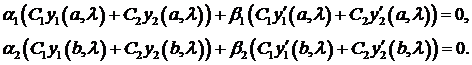
Получим алгебраическую линейную однородную систему относительно 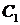 и
и 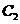 :
:
 (4)
(4)
Однородная система имеет ненулевое решение тогда и только тогда, когда ее определитель равен нулю:
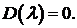 (5)
(5)
Значит, те значения 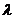 , при которых условия (2) будут выполняться, являются корнями уравнения (5). Иначе: корни
, при которых условия (2) будут выполняться, являются корнями уравнения (5). Иначе: корни  этого уравнения суть собственные значения задачи Ш. – Л. (1) – (2). Если уравнение (1) записать в виде
этого уравнения суть собственные значения задачи Ш. – Л. (1) – (2). Если уравнение (1) записать в виде 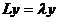 , то совокупность собственных значений – это спектр линейного оператора
, то совокупность собственных значений – это спектр линейного оператора  .
.
Пусть 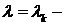 корень уравнения (5), тогда имеем ненулевое решение системы (4)
корень уравнения (5), тогда имеем ненулевое решение системы (4)  ,
, 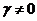 ,
, 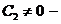 свободное неизвестное. Соответствующие собственные функции
свободное неизвестное. Соответствующие собственные функции 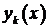 определяем по формуле (3) при
определяем по формуле (3) при  :
:

Собственные (спектральные) функции определены с точностью до постоянного множителя 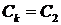 .
.
В) Свойства собственных значений и собственных функций.
Свойство 1. Краевая задача (1) – (2) имеет счетное множество собственных значений и все они вещественны. Если собственные значения рассматривать в порядке возрастания:  , то
, то 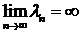 .
.
Свойство 2. Все собственные значения задачи Штурма – Лиувилля (1) – (2) простые, то есть каждому собственному значению соответствует одна собственная функция.
Свойство 3. Собственные функции, соответствующие различным собственным значениям, ортогональны на 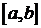 , то есть удовлетворяют равенству
, то есть удовлетворяют равенству
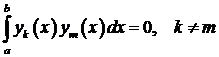 .
.
Свойство 4. Если краевые условия таковы, что
 ,
,
то все собственные числа задачи (1) – (2) неотрицательны.
Свойство 5. (Теорема Стеклова). Пусть функция  и удовлетворяет на концах отрезка условиям (2). Тогда
и удовлетворяет на концах отрезка условиям (2). Тогда  разлагается в равномерно и абсолютно сходящийся при
разлагается в равномерно и абсолютно сходящийся при  ряд Фурье по собственным функциям краевой задачи (1) – (2)
ряд Фурье по собственным функциям краевой задачи (1) – (2)
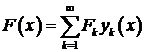 ,
,
где 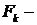 коэффициенты Фурье, определяемые по формуле:
коэффициенты Фурье, определяемые по формуле:

Задача 1. Найти собственные значения и собственные функции задачи Ш. – Л.
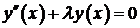 ,
, 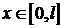
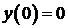 ,
, 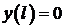 .
.
Решение. Ищем решение уравнения в виде  . Запишем характеристическое уравнение:
. Запишем характеристическое уравнение: 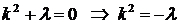 .
.
1. Пусть 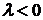 , тогда корни характеристического уравнения действительны и различны:
, тогда корни характеристического уравнения действительны и различны:  . Фундаментальная система решений
. Фундаментальная система решений 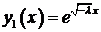 ,
, 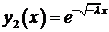 . Общее решение уравнения имеет вид:
. Общее решение уравнения имеет вид:
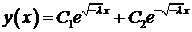 ,
,
где 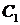 и
и  произвольные постоянные. Используя заданные краевые условия, получим систему для определения
произвольные постоянные. Используя заданные краевые условия, получим систему для определения 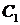 ,
, 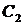 :
:
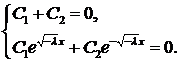
Определитель этой системы 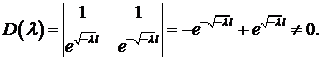 Значит, система имеет единственное решение
Значит, система имеет единственное решение 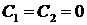 . Поэтому в случае
. Поэтому в случае 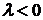 данная задача собственных значений и собственных функций не имеет.
данная задача собственных значений и собственных функций не имеет.
2. Пусть 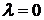 . Тогда оба корня характеристического уравнения равны нулю Фундаментальная система решений
. Тогда оба корня характеристического уравнения равны нулю Фундаментальная система решений 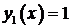 ,
,  . Общее решение уравнения – линейная функция
. Общее решение уравнения – линейная функция 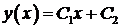 . Подставляя краевые условия, получим
. Подставляя краевые условия, получим 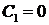 ,
, 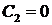 . Значит,
. Значит, 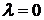 не является собственным значением рассматриваемой задачи Ш. – Л.
не является собственным значением рассматриваемой задачи Ш. – Л.
3. Пусть 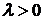 . Корни характеристического уравнения мнимые:
. Корни характеристического уравнения мнимые: 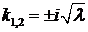 . Фундаментальная система решений
. Фундаментальная система решений 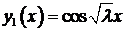 ,
,  . Общее решение уравнения
. Общее решение уравнения
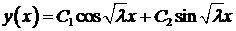 .
.
Определим 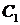 ,
, 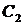 из краевых условий. При
из краевых условий. При  (на левом конце)
(на левом конце) 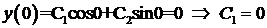 . При
. При 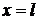 (на правом конце) получаем
(на правом конце) получаем 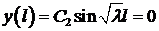 . Нас интересует нетривиальное решение, то есть
. Нас интересует нетривиальное решение, то есть 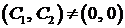 , поэтому
, поэтому 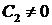 . Тогда должен быть равен нулю второй множитель
. Тогда должен быть равен нулю второй множитель

Итак, 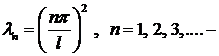 собственные значения, тогда решения
собственные значения, тогда решения 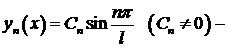 собственные функции данной задачи Ш. – Л. ●
собственные функции данной задачи Ш. – Л. ●
Замечание. Иногда в уравнении 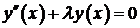 удобнее вместо
удобнее вместо 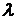 брать
брать 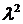 . Тогдасобственные значения задачи 1 можно записать в виде
. Тогдасобственные значения задачи 1 можно записать в виде 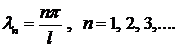
Задача 2. Найти собственные значения и собственные функции задачи Штурма – Лиувилля
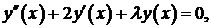
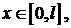
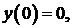

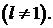
Решение. Составим характеристическое уравнение 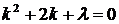 и найдем его корни
и найдем его корни 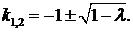
1. Пусть 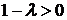 , то есть
, то есть  . Тогда корни характеристического уравнения действительны и различны. Общее решение уравнения имеет вид
. Тогда корни характеристического уравнения действительны и различны. Общее решение уравнения имеет вид
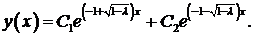
Краевые условия приводят к системе для определения 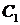 ,
, 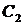 :
:
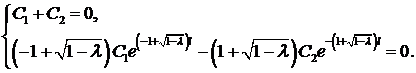
Определитель этой системы

Тривиальное решение является единственным. Значит, задача в случае 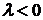 не имеет собственных значений и собственных функций.
не имеет собственных значений и собственных функций.
2. Пусть 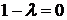 . У характеристического уравнения кратные корни
. У характеристического уравнения кратные корни 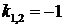 . Общее решение
. Общее решение 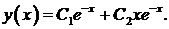 Из краевых условий получим систему
Из краевых условий получим систему

Отсюда 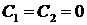 , так как по условию
, так как по условию 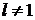 . Значит,
. Значит, 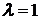 не является собственным значением.
не является собственным значением.
3. Пусть 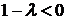 , то есть
, то есть 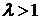 . Характеристическое уравнение имеет комплексно сопряженные корни
. Характеристическое уравнение имеет комплексно сопряженные корни 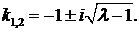 Общее решение уравнения
Общее решение уравнения
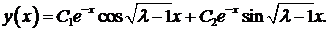
Из краевых условий получаем

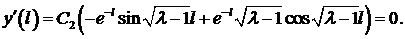
Случай 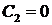 дает тривиальное решение, то есть нас не интересует. Выясним, при каком значении
дает тривиальное решение, то есть нас не интересует. Выясним, при каком значении 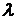 может обращаться в нуль выражение в скобках
может обращаться в нуль выражение в скобках
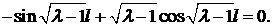
 Приходим к уравнению
Приходим к уравнению 
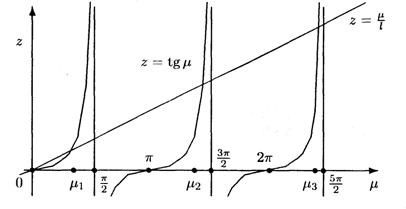
Обозначим  , тогда уравнение для определения собственных значений запишется так:
, тогда уравнение для определения собственных значений запишется так:

Это трансцендентное уравнение, которое можно решить, например, графически. Обозначим последовательные положительные корни этого уравнения  Тогда
Тогда  и
и 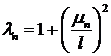 ,
,  собственные значения, а
собственные значения, а 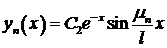 ,
, 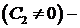 собственные функции этой задачи. ●
собственные функции этой задачи. ●
Задача 3. Найти собственные значения и собственные функции задачи Штурма – Лиувилля:
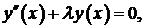
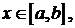
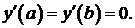
Решение. Запишем характеристическое уравнение 
1. Пусть  Тогда корни характеристического уравнения действительны и различны:
Тогда корни характеристического уравнения действительны и различны: 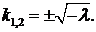 Общее решение уравнения
Общее решение уравнения
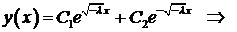
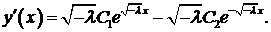
Краевые условия приводят к системе
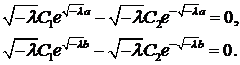
Определитель этой системы
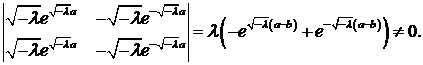
Система имеет единственное решение 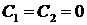 , поэтому в случае
, поэтому в случае 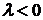 задача Ш. – Л. не имеет собственных значений и собственных функций.
задача Ш. – Л. не имеет собственных значений и собственных функций.
2. Пусть 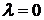 . Корни характеристического уравнения
. Корни характеристического уравнения 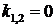 . Тогда
. Тогда

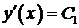 .
.
Из краевых условий находим 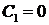 , тогда решение имеет вид
, тогда решение имеет вид 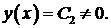 Таким образом,
Таким образом,  собственное значение,
собственное значение, 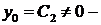 собственная функция рассматриваемой задачи Ш. – Л.
собственная функция рассматриваемой задачи Ш. – Л.
3. Пусть 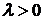 . Корни характеристического уравнения
. Корни характеристического уравнения 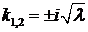 . Тогда
. Тогда

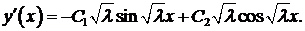
Вычислим значения производной на концах отрезка
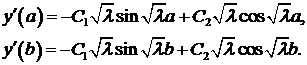
Используя краевые условия, получим систему для 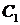 и
и 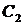 :
:

Определитель системы

Найдем те значения 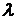 , при которых определитель равен нулю.
, при которых определитель равен нулю.
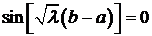

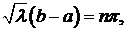
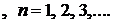 .
.
Собственные значения задачи 
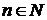 . Подставляя найденные
. Подставляя найденные 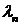 в первое (например) уравнение системы, находим
в первое (например) уравнение системы, находим
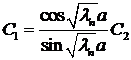 .
.
Из общего решения получаем собственные функции
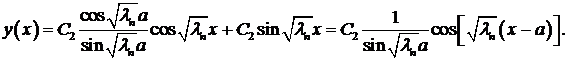
Итак, рассматриваемая задача Ш. – Л. имеет собственные значения 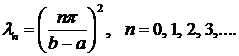 (подключили сюда
(подключили сюда 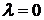 ) и собственные функции
) и собственные функции
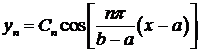 ,
, 
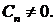
В частности, если  , собственные значения и собственные функции выглядят так:
, собственные значения и собственные функции выглядят так:
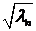 :
: 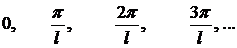
 :
: 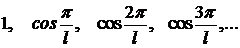 ●
●
Задачи для самостоятельного решения
- Показать, что
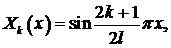
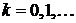 суть собственные функции задачи Штурма – Лиувилля:
суть собственные функции задачи Штурма – Лиувилля:
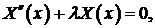
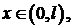
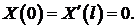
- Убедиться, что
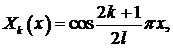
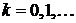 – собственные функции задачи Штурма –Лиувилля:
– собственные функции задачи Штурма –Лиувилля:
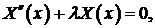

- Показать, что
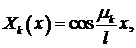
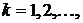 где
где 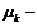 положительные корни трансцендентного уравнения
положительные корни трансцендентного уравнения  являются собственными функциями задачи Штурма-Лиувилля:
являются собственными функциями задачи Штурма-Лиувилля:
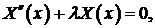
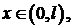

- Решить следующие задачи Штурма-Лиувилля:
a) 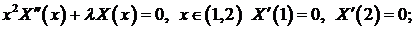
b) 
c) 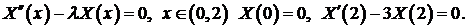
Закрепленной на концах
Метод Фурье (метод разделения переменных) является одним из наиболее распространенных методов решения уравнений с частными производными. Подробное изложение метода проведем для задачи о свободных колебаниях струны, концы которой закреплены.
Задача сводится к решению однородного уравнения
 (1)
(1)
при начальных условиях
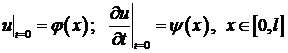 (2)
(2)
и краевых условиях
 (3)
(3)
Метод разделения переменных (метод Фурье) состоит в том, что сначала решается основная вспомогательная задача. А именно, разыскиваются нетривиальные решения однородного уравнения (1), удовлетворяющие однородным краевым условиям (3), в виде
 (4)
(4)
Дифференцируем функцию (4) дважды по 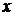 и по
и по 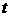 :
:
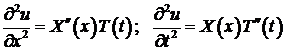
и подставляем эти производные в уравнение(1): 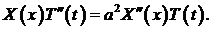
Переменные разделяются:
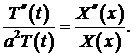 (5)
(5)
Так как функция (4) – предполагаемое решение уравнения (1), равенство (5) должно выполняться тождественно в области 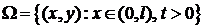 . Но правая часть равенства (5) не зависит от
. Но правая часть равенства (5) не зависит от  , а левая – от
, а левая – от  , поэтому в обеих частях равенства (5) должна быть постоянная величина, которую обозначим
, поэтому в обеих частях равенства (5) должна быть постоянная величина, которую обозначим 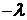 .
.
 (6)
(6)
Отсюда следует, что функции  и
и  суть решения обыкновенных дифференциальных уравнений:
суть решения обыкновенных дифференциальных уравнений:

Займемся сначала функцией 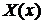 . Из граничных условий (3) и представления (4) следует:
. Из граничных условий (3) и представления (4) следует: 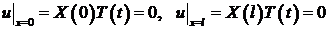 для всех
для всех 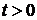 .
.
Так как 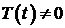 (ищем нетривиальные решения!), то должно быть
(ищем нетривиальные решения!), то должно быть 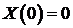 и
и 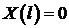 . Получили к краевую задачу для функции
. Получили к краевую задачу для функции 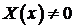 :
:
 (7)
(7)
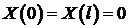 (8)
(8)
Пришли к задаче Штурма – Лиувилля: требуется найти такие значения параметра 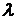 (собственные значения), при которых задача (7) – (8) имеет нетривиальные решения, и найти эти решения (собственные функции).
(собственные значения), при которых задача (7) – (8) имеет нетривиальные решения, и найти эти решения (собственные функции).
Выше (см. замечание к задаче 1 п.1) было показано, что вместо постоянной 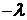 можно взять
можно взять 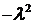 . В той же задача 1 были найдены собственные значения
. В той же задача 1 были найдены собственные значения 
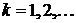 и собственные функции
и собственные функции
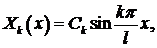
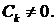
Как и должно быть, полученные собственные функции ортогональны на  , то есть
, то есть
 при
при 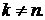
Теперь следует отыскать функцию  . Функция
. Функция 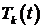 , соответствующая собственному значению
, соответствующая собственному значению  , удовлетворяет уравнению
, удовлетворяет уравнению

общее решение которого имеет вид:

Подставляя найденные функции 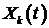 и
и 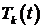 в формулу (4), получим множество решений уравнения (1), удовлетворяющих краевым условиям (3):
в формулу (4), получим множество решений уравнения (1), удовлетворяющих краевым условиям (3):
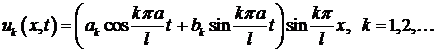 (9)
(9)
Здесь введены обозначения 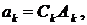
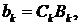
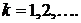
Решения (9) называются собственными функциями задачи (1), (3); соответствующие им колебания струны – собственными колебаниями.
Переходим к заключительной части метода Фурье: при помощи собственных функций (9) построить решение, удовлетворяющее начальным условиям (2). Для этого составим ряд:
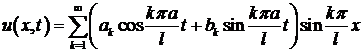 (10)
(10)
Осталось подобрать произвольные постоянные 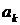 и
и  так, чтобы удовлетворить начальным условиям (2). При
так, чтобы удовлетворить начальным условиям (2). При  из соотношения (10) легко получить
из соотношения (10) легко получить
 (11)
(11)
Для второго начального условия дифференцируем ряд (10) по 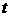 :
:

и подставляем  :
:
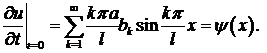 (12)
(12)
Формулы (11) и (12) означают, что числа 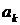 и
и  являются коэффициентами разложения начальных функций
являются коэффициентами разложения начальных функций 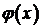 и
и 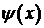 в ряд Фурье по синусам на отрезке
в ряд Фурье по синусам на отрезке 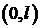 , то есть
, то есть

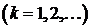 (13)
(13)
Таким образом, при реализации метода Фурье для задачи (1), (2), (3) надо разложить начальные данные 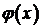 и
и 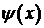 в ряд Фурье по синусам на
в ряд Фурье по синусам на 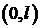 .
.
Подставив найденные 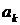 ,
,  ,
,  в ряд (10), получим формально решение задачи. Для того чтобы сумма ряда (10) была решением задачи (1), (2), (3), функции
в ряд (10), получим формально решение задачи. Для того чтобы сумма ряда (10) была решением задачи (1), (2), (3), функции  и
и 
|
|
|


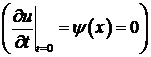 из формулы Даламбера получаем
из формулы Даламбера получаем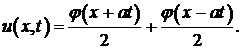
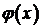 .
.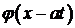 в физике называется распространяющейся волной – неизменный профиль
в физике называется распространяющейся волной – неизменный профиль  . Аналогично функция
. Аналогично функция 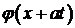 представляет неизменный профиль
представляет неизменный профиль 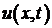 представляет собой сумму двух полуволн: прямой, бегущей вправо со скоростью
представляет собой сумму двух полуволн: прямой, бегущей вправо со скоростью 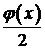 – половиной начального отклонения
– половиной начального отклонения  Рассмотрим фазовую плоскость
Рассмотрим фазовую плоскость  .
.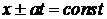 суть характеристики. Функция
суть характеристики. Функция 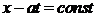 , а функция
, а функция 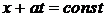 .
.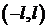 , а вне этого промежутка равно нулю.
, а вне этого промежутка равно нулю.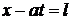 и
и 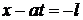 представляют собой передний и задний фронты прямой волны, а характеристики
представляют собой передний и задний фронты прямой волны, а характеристики 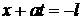 и
и 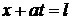 – соответственно передний и задний фронты обратной волны. Эти характеристики разбивают фазовую плоскость на несколько областей. Через область
– соответственно передний и задний фронты обратной волны. Эти характеристики разбивают фазовую плоскость на несколько областей. Через область 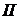
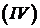 проходит прямая (обратная) волна, а в области
проходит прямая (обратная) волна, а в области 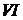 взаимодействуют обе волны. В область
взаимодействуют обе волны. В область 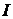 (и
(и 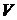 ) до некоторого момента времени
) до некоторого момента времени 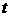 еще не дошла прямая (обратная) волна; через область
еще не дошла прямая (обратная) волна; через область  с некоторого момента
с некоторого момента 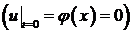 колебания вызываются начальной скоростью (или импульсом)
колебания вызываются начальной скоростью (или импульсом)  и решение задачи Коши можно представить в виде разности обратной и прямой волны:
и решение задачи Коши можно представить в виде разности обратной и прямой волны: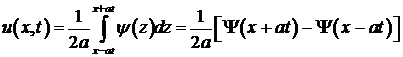
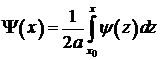 – первообразная функции
– первообразная функции 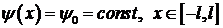 и
и 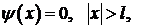 тогда
тогда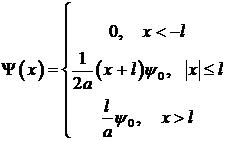
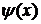 и
и 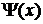 приведены на рисунке.
приведены на рисунке.

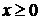 важна при изучении процесса отражения волны от края. Рассмотрим, например, задачу о распространении начального возмущения в струне с закрепленным краем.
важна при изучении процесса отражения волны от края. Рассмотрим, например, задачу о распространении начального возмущения в струне с закрепленным краем.

 (или
(или 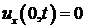 ).
). . С физической точки зрения это означает, что мы хотим задать такое начальное возмущение бесконечной струны, чтобы колебания ее участка
. С физической точки зрения это означает, что мы хотим задать такое начальное возмущение бесконечной струны, чтобы колебания ее участка 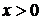 были такими же, как если бы конец
были такими же, как если бы конец  ) начальные данные следует продолжить на всю прямую нечетным образом. Тогда из формулы Даламбера при
) начальные данные следует продолжить на всю прямую нечетным образом. Тогда из формулы Даламбера при 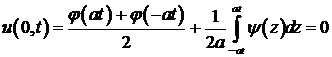
 и
и  .
.
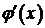 от четной функции является нечетной.
от четной функции является нечетной. Например, пусть в задаче для полубесконечной струны с закрепленным краем начальное отклонение отлично от нуля только в промежутке
Например, пусть в задаче для полубесконечной струны с закрепленным краем начальное отклонение отлично от нуля только в промежутке 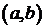 и имеет форму треугольника; начальная скорость равна нулю. Строим нечетное продолжение начального отклонения и смотрим, что происходит на фазовой плоскости (нас интересует реальная струна, то есть область
и имеет форму треугольника; начальная скорость равна нулю. Строим нечетное продолжение начального отклонения и смотрим, что происходит на фазовой плоскости (нас интересует реальная струна, то есть область 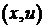 . В заштрихованных полосах отклонение отлично от нуля. Знаки плюс и минус указывают на знак фазы отклонения.
. В заштрихованных полосах отклонение отлично от нуля. Знаки плюс и минус указывают на знак фазы отклонения. – процесс отражения обратной волны от закрепленного края, область
– процесс отражения обратной волны от закрепленного края, область  – отраженная волна (в противофазе).
– отраженная волна (в противофазе).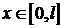 , продолжаем начальные данные для закрепленных концов нечетным образом влево от
, продолжаем начальные данные для закрепленных концов нечетным образом влево от 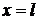 . Для свободных концов продолжаем начальные данные четным образом.
. Для свободных концов продолжаем начальные данные четным образом. . Ответ:
. Ответ: 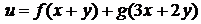 .
.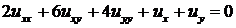 . Ответ:
. Ответ: 
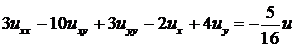 . Ответ:
. Ответ: 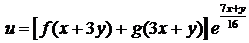 .
. . Ответ:
. Ответ: 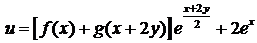 .
.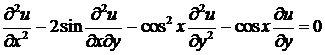 .
. .
. . Ответ:
. Ответ: 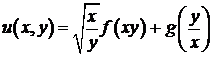 .
.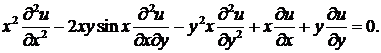
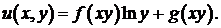
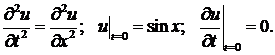
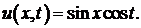
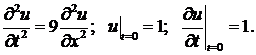

 ,
, .
. .
. .
. .
.
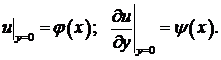
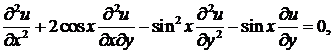
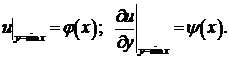
 .
.
 На фазовой плоскости проследить за процессом при изменении
На фазовой плоскости проследить за процессом при изменении 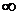 (вдоль вертикали) и при изменении
(вдоль вертикали) и при изменении 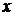 от
от 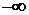 до
до  (вдоль горизонтали).
(вдоль горизонтали). 2) Бесконечной струне на отрезке
2) Бесконечной струне на отрезке 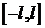 сообщена поперечная начальная скорость
сообщена поперечная начальная скорость 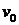 , вне этого отрезка начальная скорость равна нулю. Построить профиль струны для моментов времени
, вне этого отрезка начальная скорость равна нулю. Построить профиль струны для моментов времени 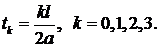
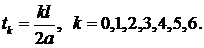 На фазовой плоскости проследить за процессом.
На фазовой плоскости проследить за процессом. 4) Конечная струна, закрепленная на концах
4) Конечная струна, закрепленная на концах 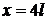 , возмущена начальным отклонением (см. рис.). Построить профиль струны для моментов времени
, возмущена начальным отклонением (см. рис.). Построить профиль струны для моментов времени 
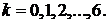 На фазовой плоскости проследить за процессом.
На фазовой плоскости проследить за процессом. при которых уравнение
при которых уравнение (1)
(1)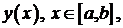 удовлетворяющие однородным краевым условиям
удовлетворяющие однородным краевым условиям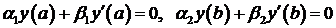 , (2)
, (2)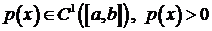 при
при 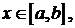
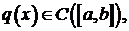

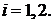 Предполагается, что решение задачи
Предполагается, что решение задачи 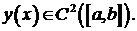 Значение параметра
Значение параметра 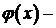 собственной функцией.
собственной функцией.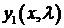 ,
, 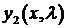 уравнения (1). Общее решение этого уравнения имеет вид
уравнения (1). Общее решение этого уравнения имеет вид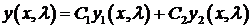 (3)
(3) – произвольные постоянные. Так как нас интересуют только нетривиальные решения, то должно быть
– произвольные постоянные. Так как нас интересуют только нетривиальные решения, то должно быть 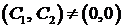 .
.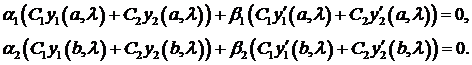
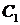 и
и 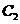 :
: (4)
(4)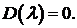 (5)
(5)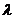 , при которых условия (2) будут выполняться, являются корнями уравнения (5). Иначе: корни
, при которых условия (2) будут выполняться, являются корнями уравнения (5). Иначе: корни  этого уравнения суть собственные значения задачи Ш. – Л. (1) – (2). Если уравнение (1) записать в виде
этого уравнения суть собственные значения задачи Ш. – Л. (1) – (2). Если уравнение (1) записать в виде 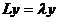 , то совокупность собственных значений – это спектр линейного оператора
, то совокупность собственных значений – это спектр линейного оператора  .
.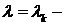 корень уравнения (5), тогда имеем ненулевое решение системы (4)
корень уравнения (5), тогда имеем ненулевое решение системы (4)  ,
, 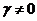 ,
, 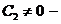 свободное неизвестное. Соответствующие собственные функции
свободное неизвестное. Соответствующие собственные функции 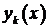 определяем по формуле (3) при
определяем по формуле (3) при  :
:
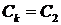 .
. , то
, то 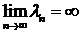 .
.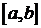 , то есть удовлетворяют равенству
, то есть удовлетворяют равенству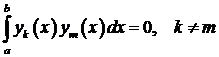 .
. ,
, и удовлетворяет на концах отрезка условиям (2). Тогда
и удовлетворяет на концах отрезка условиям (2). Тогда 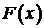 разлагается в равномерно и абсолютно сходящийся при
разлагается в равномерно и абсолютно сходящийся при 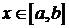 ряд Фурье по собственным функциям краевой задачи (1) – (2)
ряд Фурье по собственным функциям краевой задачи (1) – (2)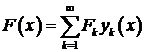 ,
,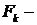 коэффициенты Фурье, определяемые по формуле:
коэффициенты Фурье, определяемые по формуле:
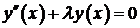 ,
, 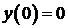 ,
, 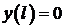 .
. . Запишем характеристическое уравнение:
. Запишем характеристическое уравнение: 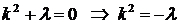 .
.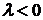 , тогда корни характеристического уравнения действительны и различны:
, тогда корни характеристического уравнения действительны и различны:  . Фундаментальная система решений
. Фундаментальная система решений 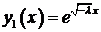 ,
, 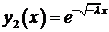 . Общее решение уравнения имеет вид:
. Общее решение уравнения имеет вид: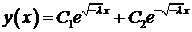 ,
, произвольные постоянные. Используя заданные краевые условия, получим систему для определения
произвольные постоянные. Используя заданные краевые условия, получим систему для определения 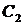 :
: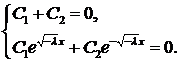
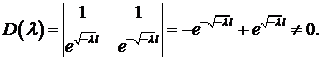 Значит, система имеет единственное решение
Значит, система имеет единственное решение 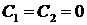 . Поэтому в случае
. Поэтому в случае 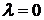 . Тогда оба корня характеристического уравнения равны нулю Фундаментальная система решений
. Тогда оба корня характеристического уравнения равны нулю Фундаментальная система решений 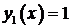 ,
,  . Общее решение уравнения – линейная функция
. Общее решение уравнения – линейная функция 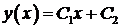 . Подставляя краевые условия, получим
. Подставляя краевые условия, получим 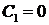 ,
, 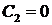 . Значит,
. Значит, 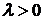 . Корни характеристического уравнения мнимые:
. Корни характеристического уравнения мнимые: 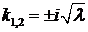 . Фундаментальная система решений
. Фундаментальная система решений 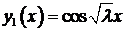 ,
,  . Общее решение уравнения
. Общее решение уравнения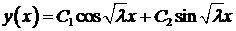 .
.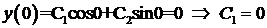 . При
. При 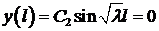 . Нас интересует нетривиальное решение, то есть
. Нас интересует нетривиальное решение, то есть 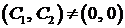 , поэтому
, поэтому 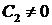 . Тогда должен быть равен нулю второй множитель
. Тогда должен быть равен нулю второй множитель
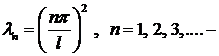 собственные значения, тогда решения
собственные значения, тогда решения 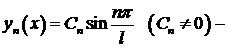 собственные функции данной задачи Ш. – Л. ●
собственные функции данной задачи Ш. – Л. ●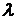 брать
брать 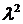 . Тогдасобственные значения задачи 1 можно записать в виде
. Тогдасобственные значения задачи 1 можно записать в виде 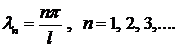
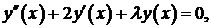
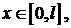
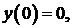

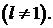
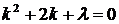 и найдем его корни
и найдем его корни 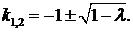
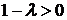 , то есть
, то есть  . Тогда корни характеристического уравнения действительны и различны. Общее решение уравнения имеет вид
. Тогда корни характеристического уравнения действительны и различны. Общее решение уравнения имеет вид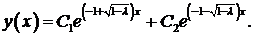
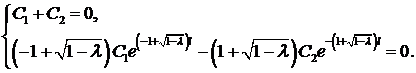

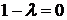 . У характеристического уравнения кратные корни
. У характеристического уравнения кратные корни 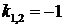 . Общее решение
. Общее решение 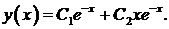 Из краевых условий получим систему
Из краевых условий получим систему
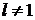 . Значит,
. Значит, 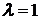 не является собственным значением.
не является собственным значением.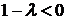 , то есть
, то есть 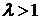 . Характеристическое уравнение имеет комплексно сопряженные корни
. Характеристическое уравнение имеет комплексно сопряженные корни 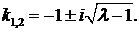 Общее решение уравнения
Общее решение уравнения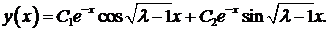

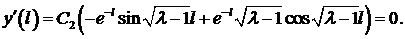
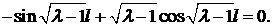
 Приходим к уравнению
Приходим к уравнению 
 , тогда уравнение для определения собственных значений запишется так:
, тогда уравнение для определения собственных значений запишется так:
 Тогда
Тогда  и
и 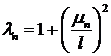 ,
,  собственные значения, а
собственные значения, а 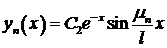 ,
, 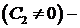 собственные функции этой задачи. ●
собственные функции этой задачи. ●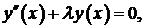
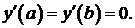

 Тогда корни характеристического уравнения действительны и различны:
Тогда корни характеристического уравнения действительны и различны: 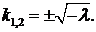 Общее решение уравнения
Общее решение уравнения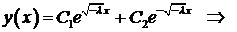
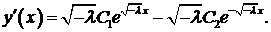
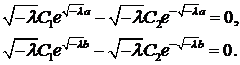
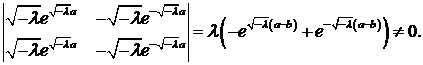
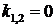 . Тогда
. Тогда
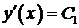 .
.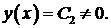 Таким образом,
Таким образом,  собственное значение,
собственное значение, 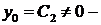 собственная функция рассматриваемой задачи Ш. – Л.
собственная функция рассматриваемой задачи Ш. – Л.
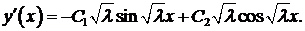
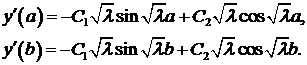


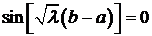

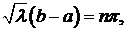
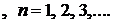 .
.
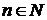 . Подставляя найденные
. Подставляя найденные 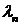 в первое (например) уравнение системы, находим
в первое (например) уравнение системы, находим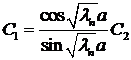 .
.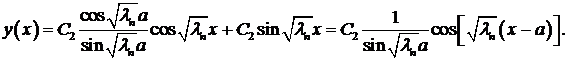
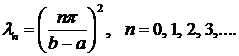 (подключили сюда
(подключили сюда 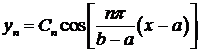 ,
, 
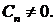
 , собственные значения и собственные функции выглядят так:
, собственные значения и собственные функции выглядят так: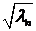 :
: 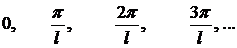
 :
: 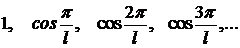 ●
●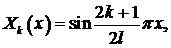
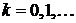 суть собственные функции задачи Штурма – Лиувилля:
суть собственные функции задачи Штурма – Лиувилля: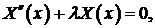
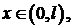
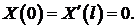
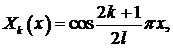

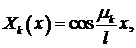
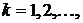 где
где 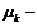 положительные корни трансцендентного уравнения
положительные корни трансцендентного уравнения  являются собственными функциями задачи Штурма-Лиувилля:
являются собственными функциями задачи Штурма-Лиувилля:
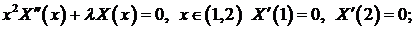

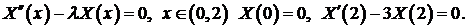
 (1)
(1) (2)
(2) (3)
(3) (4)
(4)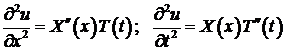
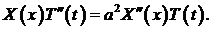
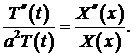 (5)
(5)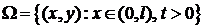 . Но правая часть равенства (5) не зависит от
. Но правая часть равенства (5) не зависит от 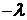 .
. (6)
(6) и
и  суть решения обыкновенных дифференциальных уравнений:
суть решения обыкновенных дифференциальных уравнений:
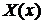 . Из граничных условий (3) и представления (4) следует:
. Из граничных условий (3) и представления (4) следует: 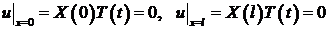 для всех
для всех 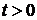 .
.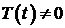 (ищем нетривиальные решения!), то должно быть
(ищем нетривиальные решения!), то должно быть 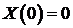 и
и 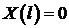 . Получили к краевую задачу для функции
. Получили к краевую задачу для функции 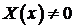 :
: (7)
(7)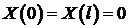 (8)
(8)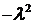 . В той же задача 1 были найдены собственные значения
. В той же задача 1 были найдены собственные значения 
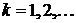 и собственные функции
и собственные функции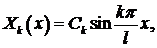
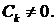
 , то есть
, то есть при
при 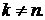
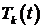 , соответствующая собственному значению
, соответствующая собственному значению  , удовлетворяет уравнению
, удовлетворяет уравнению

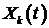 и
и 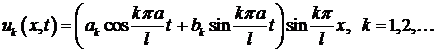 (9)
(9)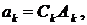
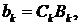
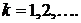
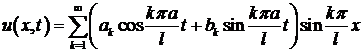 (10)
(10)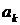 и
и  так, чтобы удовлетворить начальным условиям (2). При
так, чтобы удовлетворить начальным условиям (2). При  из соотношения (10) легко получить
из соотношения (10) легко получить (11)
(11)
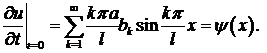 (12)
(12) являются коэффициентами разложения начальных функций
являются коэффициентами разложения начальных функций 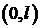 , то есть
, то есть
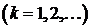 (13)
(13)