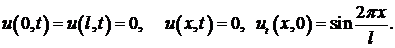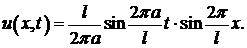Закрепленной на концах
Метод Фурье (метод разделения переменных) является одним из наиболее распространенных методов решения уравнений с частными производными. Подробное изложение метода проведем для задачи о свободных колебаниях струны, концы которой закреплены.
Задача сводится к решению однородного уравнения
 (1)
(1)
при начальных условиях
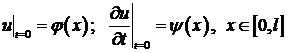 (2)
(2)
и краевых условиях
 (3)
(3)
Метод разделения переменных (метод Фурье) состоит в том, что сначала решается основная вспомогательная задача. А именно, разыскиваются нетривиальные решения однородного уравнения (1), удовлетворяющие однородным краевым условиям (3), в виде
 (4)
(4)
Дифференцируем функцию (4) дважды по 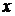 и по
и по 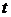 :
:
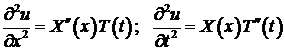
и подставляем эти производные в уравнение(1): 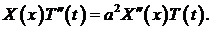
Переменные разделяются:
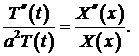 (5)
(5)
Так как функция (4) – предполагаемое решение уравнения (1), равенство (5) должно выполняться тождественно в области 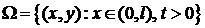 . Но правая часть равенства (5) не зависит от
. Но правая часть равенства (5) не зависит от 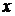 , а левая – от
, а левая – от 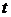 , поэтому в обеих частях равенства (5) должна быть постоянная величина, которую обозначим
, поэтому в обеих частях равенства (5) должна быть постоянная величина, которую обозначим 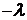 .
.
 (6)
(6)
Отсюда следует, что функции  и
и  суть решения обыкновенных дифференциальных уравнений:
суть решения обыкновенных дифференциальных уравнений:

Займемся сначала функцией 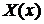 . Из граничных условий (3) и представления (4) следует:
. Из граничных условий (3) и представления (4) следует: 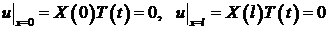 для всех
для всех 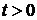 .
.
Так как 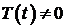 (ищем нетривиальные решения!), то должно быть
(ищем нетривиальные решения!), то должно быть 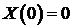 и
и 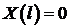 . Получили к краевую задачу для функции
. Получили к краевую задачу для функции 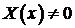 :
:
 (7)
(7)
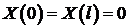 (8)
(8)
Пришли к задаче Штурма – Лиувилля: требуется найти такие значения параметра 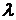 (собственные значения), при которых задача (7) – (8) имеет нетривиальные решения, и найти эти решения (собственные функции).
(собственные значения), при которых задача (7) – (8) имеет нетривиальные решения, и найти эти решения (собственные функции).
Выше (см. замечание к задаче 1 п.1) было показано, что вместо постоянной 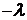 можно взять
можно взять 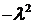 . В той же задача 1 были найдены собственные значения
. В той же задача 1 были найдены собственные значения 
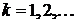 и собственные функции
и собственные функции
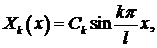
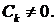
Как и должно быть, полученные собственные функции ортогональны на  , то есть
, то есть
 при
при 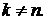
Теперь следует отыскать функцию  . Функция
. Функция 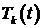 , соответствующая собственному значению
, соответствующая собственному значению  , удовлетворяет уравнению
, удовлетворяет уравнению

общее решение которого имеет вид:

Подставляя найденные функции 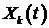 и
и 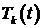 в формулу (4), получим множество решений уравнения (1), удовлетворяющих краевым условиям (3):
в формулу (4), получим множество решений уравнения (1), удовлетворяющих краевым условиям (3):
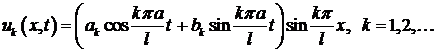 (9)
(9)
Здесь введены обозначения 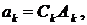
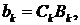
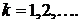
Решения (9) называются собственными функциями задачи (1), (3); соответствующие им колебания струны – собственными колебаниями.
Переходим к заключительной части метода Фурье: при помощи собственных функций (9) построить решение, удовлетворяющее начальным условиям (2). Для этого составим ряд:
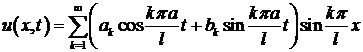 (10)
(10)
Осталось подобрать произвольные постоянные 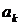 и
и  так, чтобы удовлетворить начальным условиям (2). При
так, чтобы удовлетворить начальным условиям (2). При  из соотношения (10) легко получить
из соотношения (10) легко получить
 (11)
(11)
Для второго начального условия дифференцируем ряд (10) по 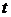 :
:

и подставляем  :
:
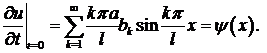 (12)
(12)
Формулы (11) и (12) означают, что числа 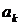 и
и  являются коэффициентами разложения начальных функций
являются коэффициентами разложения начальных функций 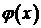 и
и 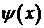 в ряд Фурье по синусам на отрезке
в ряд Фурье по синусам на отрезке 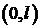 , то есть
, то есть

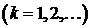 (13)
(13)
Таким образом, при реализации метода Фурье для задачи (1), (2), (3) надо разложить начальные данные 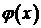 и
и 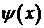 в ряд Фурье по синусам на
в ряд Фурье по синусам на 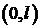 .
.
Подставив найденные 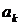 ,
,  ,
, 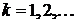 в ряд (10), получим формально решение задачи. Для того чтобы сумма ряда (10) была решением задачи (1), (2), (3), функции
в ряд (10), получим формально решение задачи. Для того чтобы сумма ряда (10) была решением задачи (1), (2), (3), функции 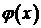 и
и 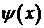 должны быть такими, чтобы ряд (10) сходился равномерно в
должны быть такими, чтобы ряд (10) сходился равномерно в 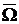 и его можно было почленно дифференцировать дважды по
и его можно было почленно дифференцировать дважды по 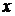 и дважды по
и дважды по 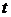 в
в 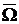 .
.
Задача 1. Однородная струна длиной  натянута между точками
натянута между точками  и
и 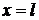 . Начальная форма струны задается функцией
. Начальная форма струны задается функцией  , начальная скорость равна нулю. Определить отклонение
, начальная скорость равна нулю. Определить отклонение 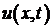 . Внешние силы отсутствуют.
. Внешние силы отсутствуют.
Решение. Требуется решать задачу о свободных колебаниях струны, закрепленной на концах. Начальное отклонение задано, начальная скорость равна нулю:
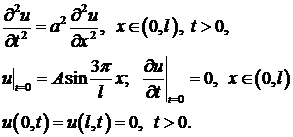
Так как по условию начальная скорость равна нулю, в формуле (10), дающей решение задачи, следует положить 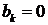 . Тогда
. Тогда
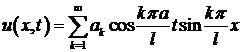 (*)
(*)
Остаётся в соответствии с (13) найти 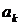 – коэффициенты Фурье начальной функции
– коэффициенты Фурье начальной функции  :
:
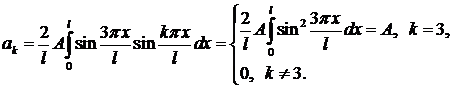
При 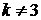 все коэффициенты
все коэффициенты 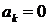 в силу ортогональности собственных функций – из коэффициентов
в силу ортогональности собственных функций – из коэффициентов 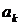 отличен от нуля только
отличен от нуля только 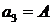 . Это естественно, так как начальное положение струны совпадает с графиком одной из собственных функций, а именно
. Это естественно, так как начальное положение струны совпадает с графиком одной из собственных функций, а именно  .
.
Можно получить этот результат и из других соображений. Запишем подробнее разложение начальной функции 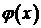 в ряд Фурье по
в ряд Фурье по 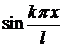 и приравняем заданной функции
и приравняем заданной функции  :
:
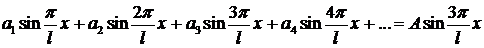
В силу единственности разложения в ряд Фурье отсюда следует, что
 , то есть
, то есть 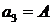 ,
, 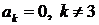 .
.
Таким образом, из ряда (*) остается только одно слагаемое
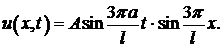
Легко убедиться, что найденная функция 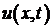 удовлетворяет и уравнению, и начальным, и граничным условиям.
удовлетворяет и уравнению, и начальным, и граничным условиям.
Решение можно записать в виде  где обозначено
где обозначено 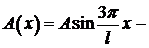 это амплитуда колебаний, зависящая от абсциссы точки струны. Все точки струны совершают гармонические колебания с одной и той же частотой
это амплитуда колебаний, зависящая от абсциссы точки струны. Все точки струны совершают гармонические колебания с одной и той же частотой 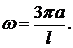 При этом точки струны одновременно достигают своего максимального отклонения и одновременно проходят положение равновесия. Такие колебания струны называются стоячими волнами. ●
При этом точки струны одновременно достигают своего максимального отклонения и одновременно проходят положение равновесия. Такие колебания струны называются стоячими волнами. ●
Физическая интерпретация
Группу слагаемых  из правой части формулы (10) преобразуем к виду
из правой части формулы (10) преобразуем к виду  .
.
Здесь обозначено 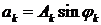 ,
,  .
.
Теперь решение задачи (1)-(2)-(3) можно записать в виде
 ,
,
где каждое слагаемое представляет собой стоячую волну, при которой точка 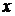 струны совершает колебания с амплитудой
струны совершает колебания с амплитудой  , частотой
, частотой 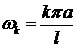 и фазой
и фазой  .
.
При колебании струна издает звук, высота которого зависит от частоты колебаний, частота самого низкого – основного тона – определяется соотношением  . Более высоким частотам соответствуют обертоны. Если, как в рассмотренной задаче, все частоты кратны основной частоте (
. Более высоким частотам соответствуют обертоны. Если, как в рассмотренной задаче, все частоты кратны основной частоте ( и
и
т.д.), то колебания называются гармоническими. Первый тон называется первой гармоникой и т.д. Решение  складывается из отдельных гармоник. Их амплитуды – и влияние на звук – быстро убывают с увеличением номера. Поэтому действие последующих гармоник сводится к созданию тембра звука.
складывается из отдельных гармоник. Их амплитуды – и влияние на звук – быстро убывают с увеличением номера. Поэтому действие последующих гармоник сводится к созданию тембра звука.

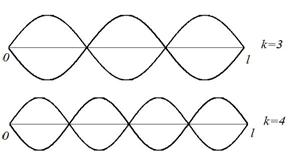
На рисунках показаны первые четыре гармоники.
Точки 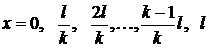 , где амплитуда
, где амплитуда 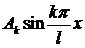 равна нулю, называются узлами
равна нулю, называются узлами 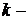 ой гармоники. У первой гармоники 2 узла, совпадающие с концами струны, у второй – три узла, у третьей – четыре и т.д.
ой гармоники. У первой гармоники 2 узла, совпадающие с концами струны, у второй – три узла, у третьей – четыре и т.д.
Точки, где амплитуда достигает наибольшего значения (то есть  ), называются пучностями
), называются пучностями 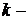 ой гармоники:
ой гармоники:

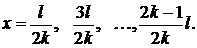
У первой гармоники одна пучность – в центре струны, у второй – две и т.д.
Если прижать звучащую струну точно в середине – в пучности основного тона, то обратятся в 0 амплитуды всех нечетных гармоник. Самой низкой окажется частота 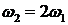 , то есть основным тоном станет звук с частотой
, то есть основным тоном станет звук с частотой  .
.
Формула 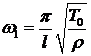 , определяющая частоту основного тона, объясняет известные из экспериментов законы звучания струны.
, определяющая частоту основного тона, объясняет известные из экспериментов законы звучания струны.
1. При заданных  и
и 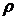 частота обратно пропорциональна длине
частота обратно пропорциональна длине  струны.
струны.
2. При заданных длине  и линейной плотности
и линейной плотности 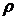 струны частота меняется прямо пропорционально корню квадратному из натяжения
струны частота меняется прямо пропорционально корню квадратному из натяжения  .
.
3. При заданных  и
и  частота меняется обратно пропорционально корню квадратному из линейной плотности
частота меняется обратно пропорционально корню квадратному из линейной плотности 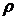 струны.
струны.
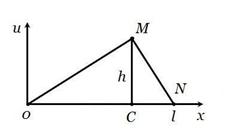 Задача 2. Однородная струна длиной
Задача 2. Однородная струна длиной  натянута между двумя точками
натянута между двумя точками  и
и 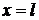 . В точке
. В точке 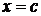 струна оттягивается на небольшое расстояние
струна оттягивается на небольшое расстояние 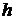 от положения равновесия и в момент
от положения равновесия и в момент  отпускается без начальной скорости. Определить отклонение струны для любого момента времени.
отпускается без начальной скорости. Определить отклонение струны для любого момента времени.
Решение. В начальный момент времени  струна занимает положение, изображенное на рисунке. Необходимо описать положение струны в любой момент времени
струна занимает положение, изображенное на рисунке. Необходимо описать положение струны в любой момент времени 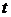 . Прежде всего запишем аналитическое представление для начального профиля струны. Для
. Прежде всего запишем аналитическое представление для начального профиля струны. Для 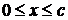 имеем
имеем  (уравнение прямой, проходящей через начало координат, угловой коэффициент
(уравнение прямой, проходящей через начало координат, угловой коэффициент 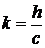 ). Для
). Для  можно воспользоваться уравнением прямой, проходящей через точки
можно воспользоваться уравнением прямой, проходящей через точки 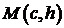 и
и  . Получаем
. Получаем  .
.
Приходим к задаче:
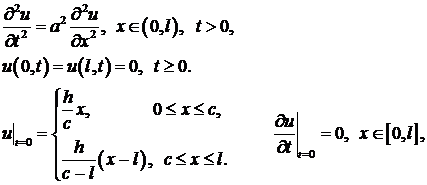
Решение задачи даётся формулой (10)
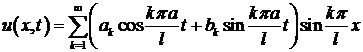 (10)
(10)
Чтобы найти коэффициенты 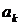 ,
,  , следует воспользоваться формулами (13).
, следует воспользоваться формулами (13).
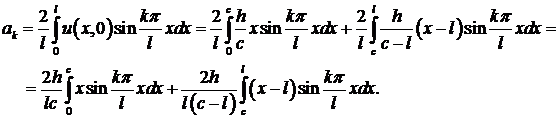
Интегралы берутся по частям
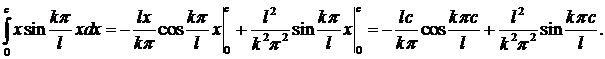
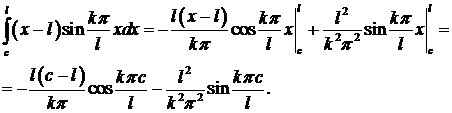
Получаем

Так как начальная скорость отсутствует, коэффициенты 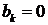 .
.
Осталось подставить найденные значения 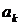 и
и  в формулу (10). Окончательно получаем:
в формулу (10). Окончательно получаем:
 ●
●
Задачи для самостоятельного решения
1. Найти колебания струны с закрепленными концами  и
и 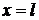 , если посередине струна оттягивается от положения равновесия на высоту
, если посередине струна оттягивается от положения равновесия на высоту 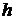 и в момент
и в момент  отпускается без начальной скорости.
отпускается без начальной скорости.
Ответ: 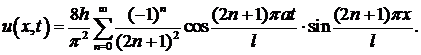
2. Пусть в условиях задачи 2, решенной в этом разделе, начальная форма струны – парабола, симметричная относительно середины струны. Максимальное отклонение равно 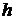 . Найти закон колебаний струны.
. Найти закон колебаний струны.
Указание. В уравнении параболы 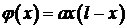 , пересекающей ось абсцисс в точках
, пересекающей ось абсцисс в точках  и
и 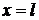 , необходимо определить коэффициент
, необходимо определить коэффициент  , зная координаты вершины параболы
, зная координаты вершины параболы 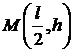 . Получим аналитическое выражение для начального профиля струны
. Получим аналитическое выражение для начального профиля струны  .
.
Ответ: 
Обратите внимание на тот факт, что амплитуда последовательных гармоник 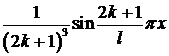 убывает быстрее, чем в задаче 1.
убывает быстрее, чем в задаче 1.
3. Пусть в начальном положении струна с закрепленными концами  и
и 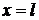 находится в покое и точкам ее на участке
находится в покое и точкам ее на участке 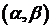 придана постоянная скорость
придана постоянная скорость 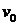 (этого можно добиться, ударяя по струне на этом участке плоским молоточком). Найти колебания струны. Исследовать частный случай
(этого можно добиться, ударяя по струне на этом участке плоским молоточком). Найти колебания струны. Исследовать частный случай  ,
,  .
.
Указание. Функция 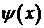 представляется в виде:
представляется в виде:
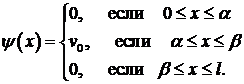
Ответ: 
В частности, при  ,
, 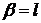 получаем:
получаем:

4. Для уравнения  в полуполосе
в полуполосе  ,
, 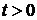 найти решение при условиях
найти решение при условиях 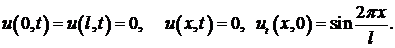
Ответ: 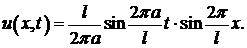



 (1)
(1)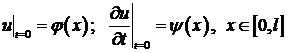 (2)
(2) (3)
(3) (4)
(4)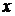 и по
и по 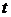 :
: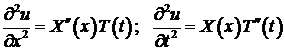
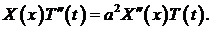
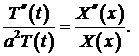 (5)
(5)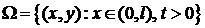 . Но правая часть равенства (5) не зависит от
. Но правая часть равенства (5) не зависит от 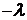 .
. (6)
(6) и
и  суть решения обыкновенных дифференциальных уравнений:
суть решения обыкновенных дифференциальных уравнений:
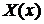 . Из граничных условий (3) и представления (4) следует:
. Из граничных условий (3) и представления (4) следует: 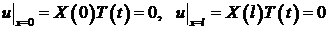 для всех
для всех 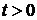 .
.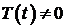 (ищем нетривиальные решения!), то должно быть
(ищем нетривиальные решения!), то должно быть 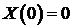 и
и 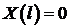 . Получили к краевую задачу для функции
. Получили к краевую задачу для функции 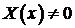 :
: (7)
(7)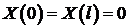 (8)
(8)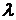 (собственные значения), при которых задача (7) – (8) имеет нетривиальные решения, и найти эти решения (собственные функции).
(собственные значения), при которых задача (7) – (8) имеет нетривиальные решения, и найти эти решения (собственные функции).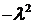 . В той же задача 1 были найдены собственные значения
. В той же задача 1 были найдены собственные значения 
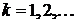 и собственные функции
и собственные функции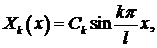
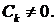
 , то есть
, то есть при
при 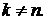
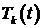 , соответствующая собственному значению
, соответствующая собственному значению  , удовлетворяет уравнению
, удовлетворяет уравнению

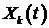 и
и 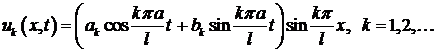 (9)
(9)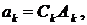
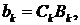
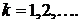
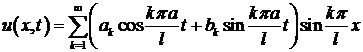 (10)
(10)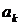 и
и  так, чтобы удовлетворить начальным условиям (2). При
так, чтобы удовлетворить начальным условиям (2). При  из соотношения (10) легко получить
из соотношения (10) легко получить (11)
(11)
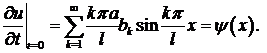 (12)
(12) являются коэффициентами разложения начальных функций
являются коэффициентами разложения начальных функций 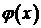 и
и 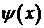 в ряд Фурье по синусам на отрезке
в ряд Фурье по синусам на отрезке 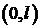 , то есть
, то есть
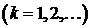 (13)
(13) и его можно было почленно дифференцировать дважды по
и его можно было почленно дифференцировать дважды по  натянута между точками
натянута между точками  и
и 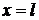 . Начальная форма струны задается функцией
. Начальная форма струны задается функцией  , начальная скорость равна нулю. Определить отклонение
, начальная скорость равна нулю. Определить отклонение 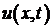 . Внешние силы отсутствуют.
. Внешние силы отсутствуют.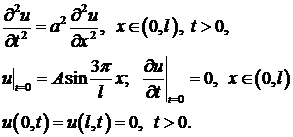
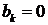 . Тогда
. Тогда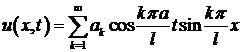 (*)
(*)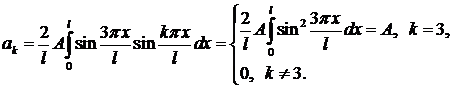
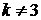 все коэффициенты
все коэффициенты 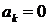 в силу ортогональности собственных функций – из коэффициентов
в силу ортогональности собственных функций – из коэффициентов 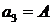 . Это естественно, так как начальное положение струны совпадает с графиком одной из собственных функций, а именно
. Это естественно, так как начальное положение струны совпадает с графиком одной из собственных функций, а именно  .
.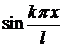 и приравняем заданной функции
и приравняем заданной функции 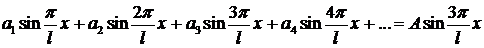
 , то есть
, то есть 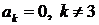 .
.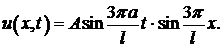
 где обозначено
где обозначено 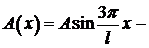 это амплитуда колебаний, зависящая от абсциссы точки струны. Все точки струны совершают гармонические колебания с одной и той же частотой
это амплитуда колебаний, зависящая от абсциссы точки струны. Все точки струны совершают гармонические колебания с одной и той же частотой 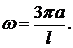 При этом точки струны одновременно достигают своего максимального отклонения и одновременно проходят положение равновесия. Такие колебания струны называются стоячими волнами. ●
При этом точки струны одновременно достигают своего максимального отклонения и одновременно проходят положение равновесия. Такие колебания струны называются стоячими волнами. ● из правой части формулы (10) преобразуем к виду
из правой части формулы (10) преобразуем к виду  .
.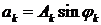 ,
,  .
. ,
, , частотой
, частотой 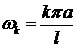 и фазой
и фазой  .
. . Более высоким частотам соответствуют обертоны. Если, как в рассмотренной задаче, все частоты кратны основной частоте (
. Более высоким частотам соответствуют обертоны. Если, как в рассмотренной задаче, все частоты кратны основной частоте ( и
и

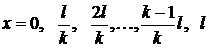 , где амплитуда
, где амплитуда 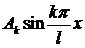 равна нулю, называются узлами
равна нулю, называются узлами 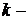 ой гармоники. У первой гармоники 2 узла, совпадающие с концами струны, у второй – три узла, у третьей – четыре и т.д.
ой гармоники. У первой гармоники 2 узла, совпадающие с концами струны, у второй – три узла, у третьей – четыре и т.д. ), называются пучностями
), называются пучностями 
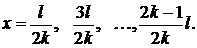
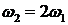 , то есть основным тоном станет звук с частотой
, то есть основным тоном станет звук с частотой  .
.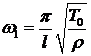 , определяющая частоту основного тона, объясняет известные из экспериментов законы звучания струны.
, определяющая частоту основного тона, объясняет известные из экспериментов законы звучания струны. и
и 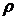 частота обратно пропорциональна длине
частота обратно пропорциональна длине  Задача 2. Однородная струна длиной
Задача 2. Однородная струна длиной 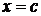 струна оттягивается на небольшое расстояние
струна оттягивается на небольшое расстояние 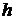 от положения равновесия и в момент
от положения равновесия и в момент 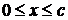 имеем
имеем  (уравнение прямой, проходящей через начало координат, угловой коэффициент
(уравнение прямой, проходящей через начало координат, угловой коэффициент 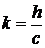 ). Для
). Для  можно воспользоваться уравнением прямой, проходящей через точки
можно воспользоваться уравнением прямой, проходящей через точки 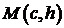 и
и  . Получаем
. Получаем  .
.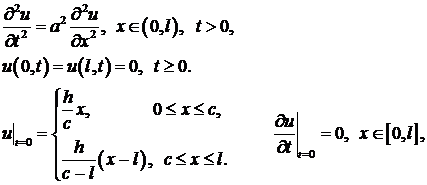
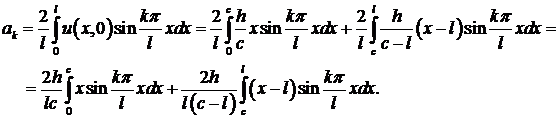
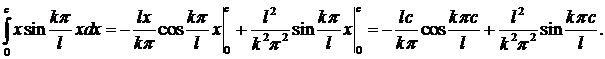
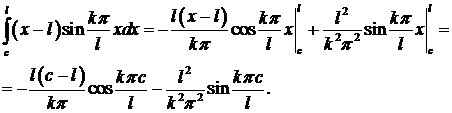

 ●
●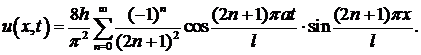
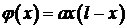 , пересекающей ось абсцисс в точках
, пересекающей ось абсцисс в точках  , зная координаты вершины параболы
, зная координаты вершины параболы 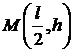 . Получим аналитическое выражение для начального профиля струны
. Получим аналитическое выражение для начального профиля струны  .
.
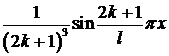 убывает быстрее, чем в задаче 1.
убывает быстрее, чем в задаче 1.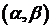 придана постоянная скорость
придана постоянная скорость 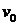 (этого можно добиться, ударяя по струне на этом участке плоским молоточком). Найти колебания струны. Исследовать частный случай
(этого можно добиться, ударяя по струне на этом участке плоским молоточком). Найти колебания струны. Исследовать частный случай  ,
, 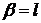 .
.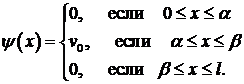


 в полуполосе
в полуполосе  ,
,