Разрабатывая теорию элементарных функций комплексной переменной Леонард Эйлер ввел комплексную переменную в качестве наиболее общего понятия переменной величины. Им в 1748 г. была получена замечательная формула, впоследствии носящая его имя, которая устанавливает связь показательной комплексной функции с тригонометрическими функциями
 ,
, 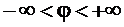 . (2.24)
. (2.24)
Так как модуль  , то при непрерывном изменении
, то при непрерывном изменении 
 точка
точка  описывает на комплексной плоскости окружность радиуса
описывает на комплексной плоскости окружность радиуса  с центром в начале координат. С помощью этой формулы можно возводить число е (основание натуральных логарифмов) в любую комплексную степень.
с центром в начале координат. С помощью этой формулы можно возводить число е (основание натуральных логарифмов) в любую комплексную степень.
Справедливы равенства:
 ,
, 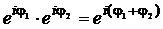 ,
,  . (2.25)
. (2.25)
Для произвольной комплексной переменной 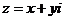 функция
функция
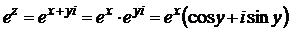 . (2.26)
. (2.26)
Используя формулу Эйлера (2.24) и тригонометрическую форму комплексного числа 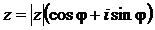 (2.13) можно записать равенство
(2.13) можно записать равенство  и получить показательную форму комплексного числа:
и получить показательную форму комплексного числа:
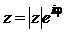 . (2.27)
. (2.27)
Показательную форму комплексного числа целесообразно использовать при умножении, делении, возведении в степень.
Если 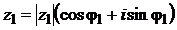 и
и  , то справедливы формулы:
, то справедливы формулы:
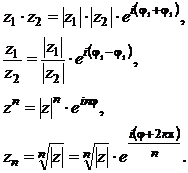 (2.28)
(2.28)
2.6. Условие заданий 1 и 2. Решение типового варианта
Задание 1. Даны два комплексных числа 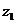 и
и 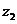 , например,
, например,
 и
и  .
.
1) Найти действительную (Re z) и мнимую (Jmz) части комплексных чисел 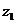 и
и 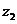 ; построить
; построить 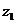 и
и 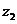 на комплексной плоскости.
на комплексной плоскости.
2) Найти  ,
,  ,
,  ,
,  . Записать числа
. Записать числа 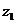 и
и 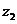 в алгебраической, тригонометрической и показательной формах.
в алгебраической, тригонометрической и показательной формах.
3) Вычислить  ,
,  , используя алгебраическую форму записи чисел.
, используя алгебраическую форму записи чисел.
4) Вычислить  и
и 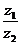 в алгебраической, тригонометрической и показательной формах.
в алгебраической, тригонометрической и показательной формах.
5) Найти 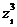 , используя тригонометрическую форму записи числа.
, используя тригонометрическую форму записи числа.
6) Найти все значения корней  , выразить их в алгебраической форме. Построить значения корней на комплексной плоскости.
, выразить их в алгебраической форме. Построить значения корней на комплексной плоскости.
Решение. Оба рассмотренных выше комплексных числа 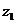 и
и 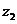 не представлены в одной из общеприняты форм. Используя формулу (2.4) выразим их в алгебраической форме.
не представлены в одной из общеприняты форм. Используя формулу (2.4) выразим их в алгебраической форме.
1)  .
.
Следовательно, 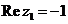 ,
,  .
.
 ,
,
 ,
, 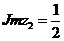 .
.
2) Изобразим 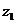 и
и 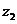 на комплексной плоскости
на комплексной плоскости 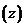 , рис. 5.
, рис. 5.
Найдем модули комплексных чисел 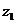 и
и 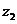 :
:
 ,
,
 .
.

Рис. 5
Из рис. 5 видно, что 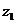 находится в III четверти, а
находится в III четверти, а 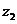 - во II-ой.
- во II-ой.
По определению из (2.12) имеем
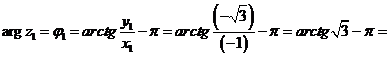
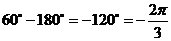 ,
,
или 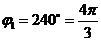 .
.
Найдем  .
.
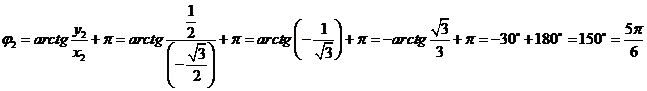 .
.
Запишем числа в тригонометрической форме:
 ,
,
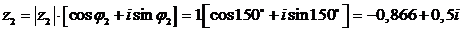 ;
;
в показательной форме:
 ,
,
 .
.
3) Запишем  и
и  в алгебраической форме:
в алгебраической форме:
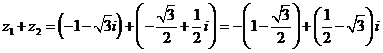 ,
,
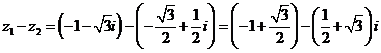 .
.
4) Вычислим  и
и 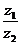 в алгебраической форме:
в алгебраической форме:
 ,
,
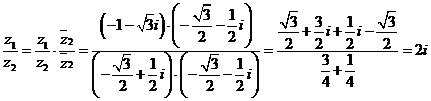 ;
;
в тригонометрической форме:
 ,
,
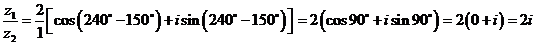 ;
;
в показательной форме:
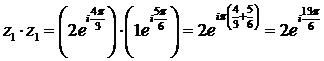 ,
,
 .
.
5) Найдем 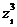 , используя тригонометрическую форму записи числа:
, используя тригонометрическую форму записи числа:
 .
.
6) Найдем все значения  , используя тригонометрическую форму, и установим их значения в алгебраической форме. Для этого воспользуемся формулой (2.23).
, используя тригонометрическую форму, и установим их значения в алгебраической форме. Для этого воспользуемся формулой (2.23).
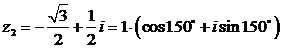
В нашем случае 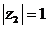 ;
;  ;
; 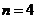 ;
;  ;
; 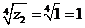 .
.
Получим значения
 ,
,  ,
,
 ,
, 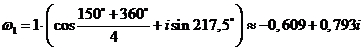 ,
,
 ,
,  ,
,
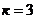 ,
, 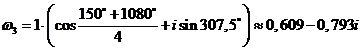 .
.
Строим корни на комплексной плоскости, рис. 6.
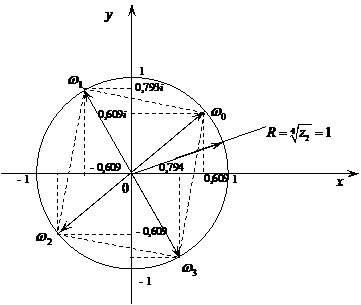
Рис. 6
Итак, корень 4-й степени из комплексного числа 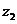 имеет 4 различных значения, которые располагаются в вершинах правильного 4-х угольника, вписанного в окружность радиусом
имеет 4 различных значения, которые располагаются в вершинах правильного 4-х угольника, вписанного в окружность радиусом  с центром в точке
с центром в точке 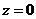 .
.
Варианты задания 1
Вариант 1.
а)  б)
б) 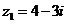
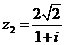

Вариант 2.
а)  б)
б) 
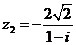

Вариант 3.
а) 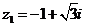 б)
б) 
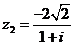

Вариант 4.
а)  б)
б) 
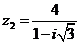
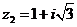
Вариант 5.
а) 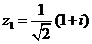 б)
б) 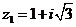


Вариант 6.
а) 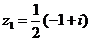 б)
б) 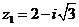
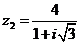
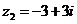
Вариант 7.
а)  б)
б) 

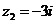
Вариант 8.
а) 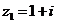 б)
б) 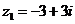
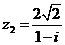
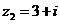
Вариант 9.
а)  б)
б) 
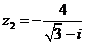
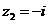
Вариант 10.
а)  б)
б) 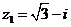

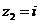
Вариант 11.
а)  б)
б) 
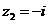

Вариант 12.
а)  б)
б) 
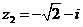

Вариант 13.
а)  б)
б) 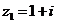
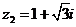
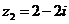
Вариант 14.
а)  б)
б) 
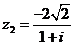

Вариант 15.
а)  б)
б) 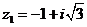
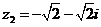

Вариант 16.
а) 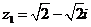 б)
б) 
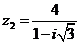
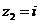
Вариант 17.
а) 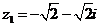 б)
б) 

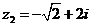
Вариант 18.
а) 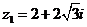 б)
б) 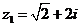


Вариант 19.
а)  б)
б) 
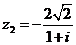
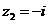
Вариант 20.
а)  б)
б) 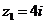
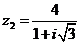

Вариант 21.
а)  б)
б) 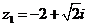
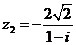

Вариант 22.
а) 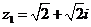 б)
б) 
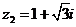

Вариант 23.
а)  б)
б) 
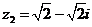

Вариант 24.
а) 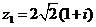 б)
б) 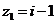


Вариант 25.
а)  б)
б) 
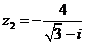

Вариант 26.
а) 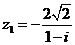 б)
б) 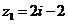


Вариант 27.
а)  б)
б) 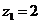
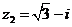
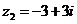
Вариант 28.
а)  б)
б) 


Вариант 29.
а)  б)
б) 
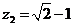

Вариант 30.
а) 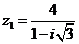 б)
б) 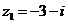


Задание 2. Вычислить значения приведенных выражений а); б).
Пример: 


Вариант 1. Вариант 2. Вариант 3.
а) 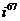 а)
а)  а)
а) 
б)  б)
б)  б)
б) 
Вариант 4. Вариант 5. Вариант 6.
а) 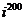 а)
а)  а)
а) 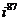
б)  б)
б) 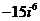 б)
б) 
Вариант 7. Вариант 8. Вариант 9.
а) 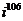 а)
а) 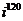 а)
а) 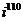
б) 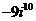 б)
б) 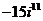 б)
б) 
Вариант 10. Вариант 11. Вариант 12.
а)  а)
а)  а)
а) 
б)  б)
б)  б)
б) 
Вариант 13. Вариант 14. Вариант 15.
а)  а)
а)  а)
а) 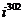
б)  б)
б)  б)
б) 
Вариант 16. Вариант 17. Вариант 18.
а)  а)
а)  а)
а) 
б)  б)
б)  б)
б) 
Вариант 19. Вариант 20. Вариант 21.
а)  а)
а) 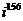 а)
а) 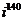
б)  б)
б) 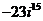 б)
б) 
Вариант 22. Вариант 23. Вариант 24.
а)  а)
а)  а)
а) 
б)  б)
б)  б)
б) 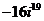
Вариант 25. Вариант 26. Вариант 27.
а)  а)
а)  а)
а) 
б)  б)
б) 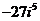 б)
б) 
Вариант 28. Вариант 29. Вариант 30.
а)  а)
а) 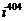 а)
а) 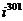
б)  б)
б)  б)
б) 
Задание 3.
Найти корни приведенных выражений а); б).
Пример: а)  ; б)
; б)  ;
;
1) Решение: 
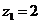 ,
,  .
.
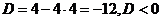 ,
,
 .
.
Ответ: 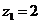 ;
;


2) Решение: 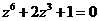
 ,
,
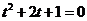
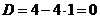
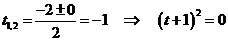
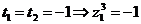

Запишем число 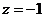 в тригонометрической форме:
в тригонометрической форме:
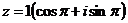
Тогда 
 ,
,
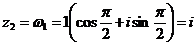 ,
,
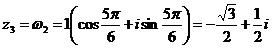 ,
,
 ,
,
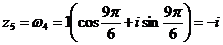
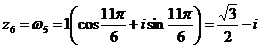
Вариант 1 Вариант 2
а) 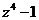 б)
б)  а)
а) 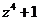 б)
б) 
Вариант 3 Вариант 4
а)  б)
б) 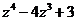 а)
а)  б)
б) 
Вариант 5 Вариант 6
а) 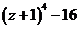 б)
б)  а)
а) 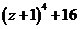 б)
б) 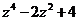
Вариант 7 Вариант 8
а)  б)
б)  а)
а) 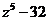 б)
б) 
Вариант 9 Вариант 10
а)  б)
б) 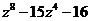 а)
а)  б)
б) 
Вариант 11 Вариант 12
а) 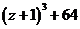 б)
б)  а)
а) 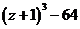 б)
б) 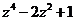
Вариант 13 Вариант 14
а) 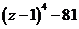 б)
б)  а)
а) 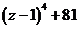 б)
б) 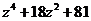
Вариант 15 Вариант 16
а) 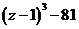 б)
б) 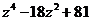 а)
а)  б)
б) 
Вариант 17 Вариант 18
а)  б)
б)  а)
а)  б)
б) 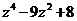
Вариант 19 Вариант 20
а)  б)
б)  а)
а)  б)
б) 
Вариант 21 Вариант 22
а) 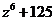 б)
б)  а)
а) 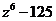 б)
б) 
Вариант 23 Вариант 24
а)  б)
б)  а)
а)  б)
б) 
Вариант 25 Вариант 26
а) 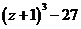 б)
б) 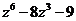 а)
а) 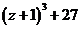 б)
б) 
Вариант 27 Вариант 28
а) 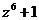 б)
б) 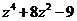 а)
а) 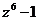 б)
б) 
Вариант 29 Вариант 30
а) 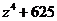 б)
б) 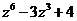 а)
а)  б)
б) 
Библиографический список
1. Рыбников К.А История математики. – М.: Издательство МГУ, 1994. -496 с.
2. Андронов И.К. Математика действительных и комплексных чисел. – М.: Просвещение, 1975 - 158 с.
3. Жевержеев В.Ф., Кальницкий Л.А., Сапогов Н.А. Специальный курс высшей математики для вузов. – М.: Высшая школа, 1970 – 416 с.
4. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисления. – М.: Наука, 1984 – 432 с.
5. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1989 – 656 с.
6. Мантуров О.В. Курс высшей математики. – М.: Высшая школа, 1996 – 448 с.
7. Рябушко А.П., Бархатов В.В., Державец В.В., Юруть И.Е. Сборник индивидуальных заданий по высшей математике. Ч. 2 – Мн.: Высшая школа, 1991. – 352 с.



 ,
, 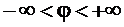 . (2.24)
. (2.24) , то при непрерывном изменении
, то при непрерывном изменении 
 точка
точка  описывает на комплексной плоскости окружность радиуса
описывает на комплексной плоскости окружность радиуса  с центром в начале координат. С помощью этой формулы можно возводить число е (основание натуральных логарифмов) в любую комплексную степень.
с центром в начале координат. С помощью этой формулы можно возводить число е (основание натуральных логарифмов) в любую комплексную степень. ,
, 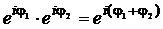 ,
,  . (2.25)
. (2.25)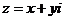 функция
функция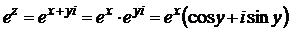 . (2.26)
. (2.26)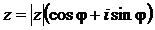 (2.13) можно записать равенство
(2.13) можно записать равенство  и получить показательную форму комплексного числа:
и получить показательную форму комплексного числа: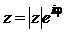 . (2.27)
. (2.27)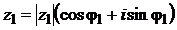 и
и  , то справедливы формулы:
, то справедливы формулы: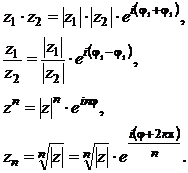 (2.28)
(2.28)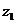 и
и 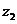 , например,
, например, и
и  .
. ,
,  ,
,  ,
,  . Записать числа
. Записать числа  ,
,  , используя алгебраическую форму записи чисел.
, используя алгебраическую форму записи чисел. и
и 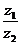 в алгебраической, тригонометрической и показательной формах.
в алгебраической, тригонометрической и показательной формах.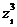 , используя тригонометрическую форму записи числа.
, используя тригонометрическую форму записи числа. , выразить их в алгебраической форме. Построить значения корней на комплексной плоскости.
, выразить их в алгебраической форме. Построить значения корней на комплексной плоскости. .
.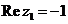 ,
,  .
. ,
, ,
, 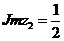 .
. , рис. 5.
, рис. 5. ,
, .
.
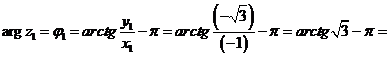
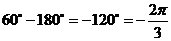 ,
,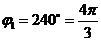 .
.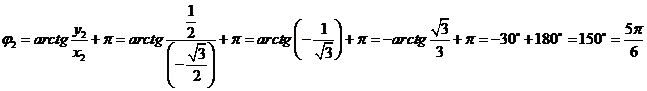 .
. ,
,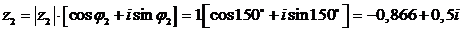 ;
; ,
, .
.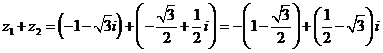 ,
,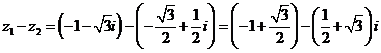 .
. ,
,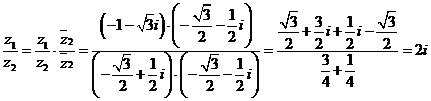 ;
; ,
,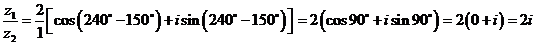 ;
;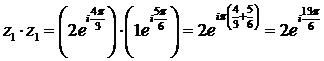 ,
, .
. .
.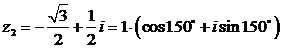
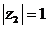 ;
;  ;
; 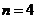 ;
;  ;
; 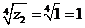 .
. ,
,  ,
, ,
, 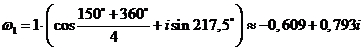 ,
, ,
,  ,
, ,
, 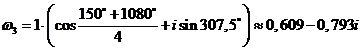 .
.
 с центром в точке
с центром в точке 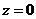 .
. б)
б) 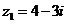
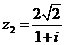

 б)
б) 
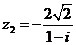

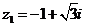 б)
б) 
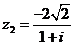

 б)
б) 
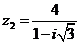
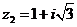
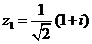 б)
б) 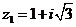

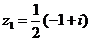 б)
б) 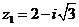
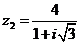
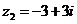
 б)
б) 

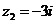
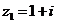 б)
б) 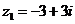
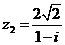
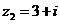
 б)
б) 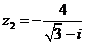
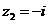
 б)
б) 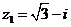

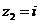
 б)
б) 
 б)
б) 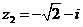
 б)
б) 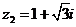
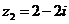
 б)
б) 
 б)
б) 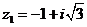
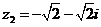
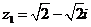 б)
б) 
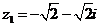 б)
б) 
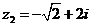
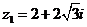 б)
б) 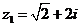

 б)
б) 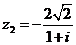
 б)
б) 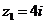

 б)
б) 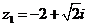
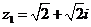 б)
б) 
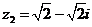

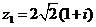 б)
б) 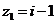
 б)
б) 
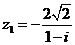 б)
б) 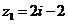

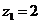
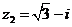
 б)
б) 


 б)
б) 
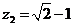

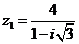 б)
б) 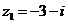




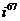 а)
а)  а)
а) 
 б)
б)  б)
б) 
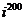 а)
а)  а)
а) 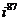
 б)
б) 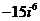 б)
б) 
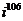 а)
а) 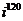 а)
а) 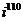
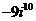 б)
б) 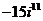 б)
б) 
 а)
а)  а)
а) 
 б)
б)  б)
б) 
 а)
а)  а)
а) 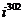
 б)
б)  б)
б) 
 а)
а) 
 б)
б)  б)
б) 
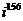 а)
а) 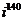
 б)
б) 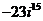 б)
б) 
 а)
а) 
 б)
б) 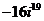
 а)
а)  а)
а) 
 б)
б) 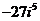 б)
б) 
 а)
а) 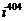 а)
а) 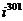
 б)
б)  б)
б) 
 ; б)
; б)  ;
; 
 .
.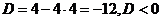 ,
, .
.

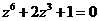
 ,
,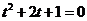
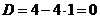
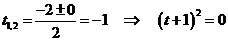
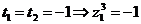

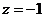 в тригонометрической форме:
в тригонометрической форме: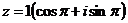

 ,
,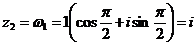 ,
,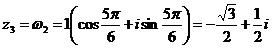 ,
, ,
,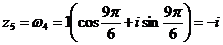
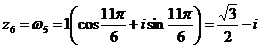
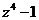 б)
б)  а)
а) 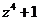 б)
б) 
 б)
б) 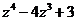 а)
а)  б)
б) 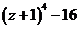 б)
б)  а)
а) 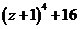 б)
б) 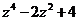
 б)
б) 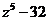 б)
б) 
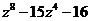 а)
а)  б)
б) 
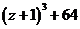 б)
б)  а)
а) 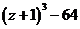 б)
б) 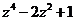
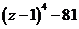 б)
б)  а)
а) 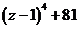 б)
б) 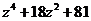
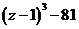 б)
б) 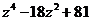 а)
а)  б)
б) 
 б)
б)  а)
а)  б)
б) 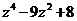
 б)
б)  а)
а)  б)
б) 
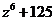 б)
б)  а)
а) 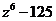 б)
б) 
 б)
б)  а)
а)  б)
б) 
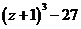 б)
б) 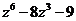 а)
а) 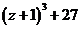 б)
б) 
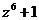 б)
б) 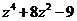 а)
а) 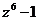 б)
б) 
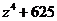 б)
б) 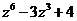 а)
а)  б)
б) 


