Комплексные числа
Методические указания и индивидуальные задания по разделу «Комплексные числа» для студентов всех специальностей
очной формы обучения
Самара 2007
УДК 517
Высшая математика: методические указания и индивидуальные задания по разделу «Комплексные числа» для студентов всех специальностей очной формы обучения / составители: В.А. Паняев, Н.М. Латыпова. – Самара: СамГАПС, 2007. – 24 с.
Утверждено на заседание кафедры 03.10.2006, протокол №2.
Печатается по решению редакционно-издательского совета академии.
Методические указания и индивидуальные задания составлены в соответствии с Государственным образовательным стандартом и действующей программой по высшей математике для технических вузов.
Составители: к.т.н., доцент В.А. Паняев
к.ф.-м.н., доцент Н.М. Латыпова
Рецензенты: к.т.н., доцент СГАУ В.В. Максимов
к.ф.-м.н., доцент СамГАПС В.Л. Шур
Под редакцией составителей
Подписано в печать 19.04.2007. Формат 60  84 1/16.
84 1/16.
Бумага офсетная. Печать офсетная. Усл. п. л. 1,5.
Тираж 150 экз. Заказ № 68.
© Самарская государственная академия путей сообщения, 2007
Комплексные числа
Геометрическое изображение комплексных чисел в декартовой
Системе координат
Всякое комплексное число  удобно изображать точкой
удобно изображать точкой  на комплексной плоскости
на комплексной плоскости 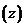 (рис. 1). Оси
(рис. 1). Оси 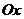 и
и 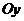 прямоугольной декартовой системы координат на этой плоскости называются соответственно действительной и мнимой осями. Между точками плоскости
прямоугольной декартовой системы координат на этой плоскости называются соответственно действительной и мнимой осями. Между точками плоскости  и изображенными на ней комплексными числами существует взаимно однозначное соответствие.
и изображенными на ней комплексными числами существует взаимно однозначное соответствие.
Одновременно с этим каждая точка  плоскости определяет вектор
плоскости определяет вектор 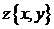 с началом в начале системы координат и концом в этой точке, проекции которого на оси координат будут соответственно х и y. Длина (модуль) этого вектора
с началом в начале системы координат и концом в этой точке, проекции которого на оси координат будут соответственно х и y. Длина (модуль) этого вектора
 . (2.8)
. (2.8)
Действительные числа 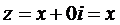 изображаются на комплексной плоскости точками (х, о) оси
изображаются на комплексной плоскости точками (х, о) оси 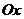 или векторами, параллельными этой оси, а число
или векторами, параллельными этой оси, а число 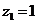 будет являться единичным вектором оси
будет являться единичным вектором оси 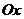 .
.
Действительные числа 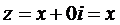 изображаются на комплексной плоскости точками (х, 0) оси
изображаются на комплексной плоскости точками (х, 0) оси 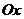 или векторами, параллельными этой оси, а число
или векторами, параллельными этой оси, а число 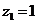 будет являться единичным вектором оси
будет являться единичным вектором оси 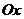 .
.
Чисто мнимым числам 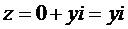 будут соответствовать точки
будут соответствовать точки  оси
оси 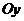 или векторы, параллельные этой оси. Число
или векторы, параллельные этой оси. Число  изображается точкой (0, 1) мнимой оси и одновременно являться единичным вектором
изображается точкой (0, 1) мнимой оси и одновременно являться единичным вектором 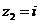 оси
оси 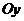 . Любая пара комплексно-сопряженных чисел z и
. Любая пара комплексно-сопряженных чисел z и  на комплексной плоскости изображается векторами
на комплексной плоскости изображается векторами 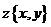 и
и  , симметричными действительной оси
, симметричными действительной оси 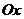 (рис. 1).
(рис. 1).
Векторы 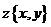 являются свободными векторами, поэтому их начало можно совмещать с любой точкой комплексной плоскости путем параллельного переноса. Сложение и вычитание комплексных чисел можно рассматривать как сложение и вычитание соответствующих векторов, совмещая их начало с точкой О (рис. 2).
являются свободными векторами, поэтому их начало можно совмещать с любой точкой комплексной плоскости путем параллельного переноса. Сложение и вычитание комплексных чисел можно рассматривать как сложение и вычитание соответствующих векторов, совмещая их начало с точкой О (рис. 2).
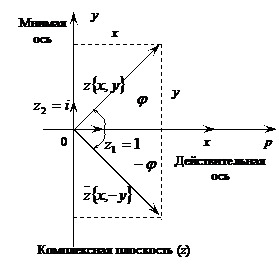
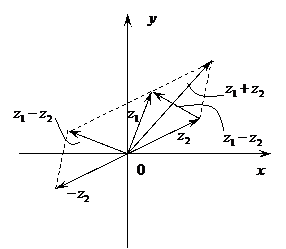
Рис. 1 Рис. 2
С помощью комплексных чисел можно задавать различные множества точек комплексной плоскости 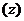 , что используется при анализе различных функций комплексной переменной и графическом изображении области их определения.
, что используется при анализе различных функций комплексной переменной и графическом изображении области их определения.
Комплексного числа
Совместим начало координат системы xOy с полюсом т. О и ось Ох с полярной осью p (рис.1) Введем в рассмотрение длину | z | вектора z { x, y } и угол φ, образованный вектором z с положительным направлением оси Ох. Этот угол называется аргументом комплексного числа и обозначается 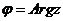 . Угол
. Угол 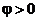 , если отсчет его производится против направления движения часовой стрелки, и
, если отсчет его производится против направления движения часовой стрелки, и 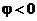 , если по часовой стрелке. Очевидно, что для всякого комплексного числа
, если по часовой стрелке. Очевидно, что для всякого комплексного числа 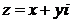 справедливы формулы:
справедливы формулы:
 ;
; 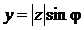 ;
;
 ;
; 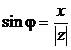 ;
; 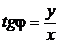 ; (2.9)
; (2.9)
где 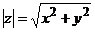 ,
,  .
.
При этом необходимо учитывать, что для любого комплексного числа его аргумент А rgz при 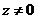 может иметь бесконечное множество значений, отличающихся одно от другого на слагаемое кратное
может иметь бесконечное множество значений, отличающихся одно от другого на слагаемое кратное 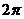 . Поэтому условия равенства комплексных чисел заключается в том, что длины (модули) должны быть равны, а аргументы φ могут отличаться на величины, кратные
. Поэтому условия равенства комплексных чисел заключается в том, что длины (модули) должны быть равны, а аргументы φ могут отличаться на величины, кратные 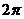 .
.
Из множества значений Argz для практических расчетов выделяют одно, лежащее в интервале  ,которое обозначают а rgz. Оно называется главным значением аргумента комплексного числа:
,которое обозначают а rgz. Оно называется главным значением аргумента комплексного числа:
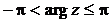 или
или  . (2.10)
. (2.10)
Очевидно 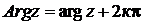 , где
, где 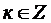 . (2.11)
. (2.11)
Для нахождения главного аргумента комплексного числа удобно использовать следующие формулы:

для точек z первой и второй четверти
комплексной плоскости,
для точек второй четверти, (2.12)
для точек третьей четверти.
Числа 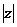 и углы
и углы  является полярными координатами точки z, т.е.
является полярными координатами точки z, т.е. 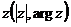 .
.
Используя алгебраическую форму 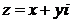 и формулы (2.9) получим тригонометрическую форму комплексного числа
и формулы (2.9) получим тригонометрическую форму комплексного числа
 . (2.13)
. (2.13)
В тригонометрическом виде комплексно-сопряженное число  , т.к.
, т.к. 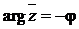 , выражается формулой
, выражается формулой
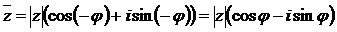 (2.14)
(2.14)
Пример. Изобразить комплексные числа 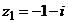 и
и 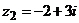 на комплексной плоскости и записать их в тригонометрической форме.
на комплексной плоскости и записать их в тригонометрической форме.
Решение. Оба числа представлены в алгебраической форме. Изобразим эти числа на комплексной плоскости и определим сначала модули 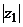 и
и 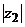 и главные аргументы
и главные аргументы  и
и 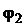 (рис. 3).
(рис. 3).
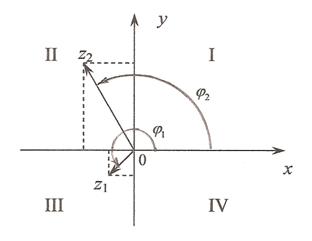
Рис. 3
1. 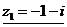
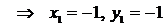 ,
,  .
.
Число 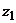 или его вектор
или его вектор  находятся в III четверти. Используя формулу (2.12) для этой четверти, имеем
находятся в III четверти. Используя формулу (2.12) для этой четверти, имеем
 , или
, или 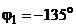 .
.
Если воспользоваться положительным значением угла 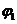 , показанным на рис. 3, тогда
, показанным на рис. 3, тогда 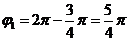 или
или 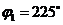 . Тригонометрическая форма числа
. Тригонометрическая форма числа 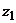 принимает вид:
принимает вид:
 или
или 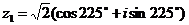 .
.
Подставив в последние формулы значения 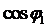 и
и 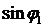 , придем к исходной алгебраической форме этого числа
, придем к исходной алгебраической форме этого числа 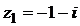 .
.
2.  ,
, 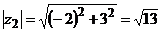 .
.
Число 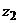 и его вектор
и его вектор 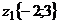 находятся во II четверти. На основании формулы (2.12) получим
находятся во II четверти. На основании формулы (2.12) получим
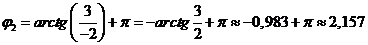 рад, или
рад, или 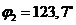 ;
;
 или
или 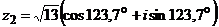 .
.
Формула Муавра
Использование комплексных чисел в тригонометрической форме удобно при выполнении над ними действий умножения, деления, возведения в степень и извлечения корня.
Умножение и деление
Пусть 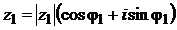 ,
,  .
.
Тогда 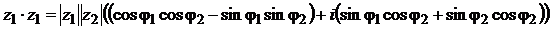 .
.
Используя известные формулы 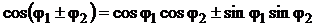 и
и 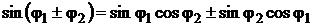 , окончательно получим:
, окончательно получим:
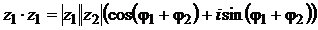 . (2.15)
. (2.15)
Доказано для любого числа сомножителей: при умножении комплексных чисел в тригонометрической форме достаточно перемножить их модули, а аргументы сложить.
Так как 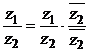 , то подставляя в это выражение
, то подставляя в это выражение 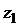 ,
, 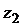 и
и 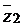 в тригонометрической форме и проводя соответствующие преобразования получим:
в тригонометрической форме и проводя соответствующие преобразования получим:
 .
.
Формула принимает вид
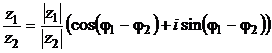 . (2.16)
. (2.16)
Для выполнения деления двух комплексных чисел в тригонометрической форме следует их модули разделить, а аргументы вычесть.
2.4.2. Возведение в натуральную степень n
Используем равенство (2.15) для возведения произвольного комплексного числа 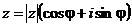 в натуральную степень n, принимая во внимание, что
в натуральную степень n, принимая во внимание, что 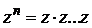 . (n раз).
. (n раз).
Получим 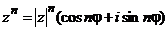 . (2.17)
. (2.17)
Равенство (2.17) называется формулой Муавра (1707 г.)
Из формулы Муавра следует, что для возведения комплексного числа в любую натуральную степень необходимо его модуль возвести в эту степень, а аргумент умножить на показатель степени.
При 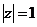 формула (2.16) принимает вид
формула (2.16) принимает вид
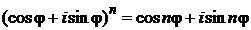 . (2.18)
. (2.18)
Замечание. Если комплексное число задано в алгебраической форме, для возведения его в степень по формуле Муавра необходимо предварительно записать число в тригонометрической форме, найдя модуль 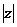 и главный аргумент
и главный аргумент 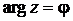 .
.
Библиографический список
1. Рыбников К.А История математики. – М.: Издательство МГУ, 1994. -496 с.
2. Андронов И.К. Математика действительных и комплексных чисел. – М.: Просвещение, 1975 - 158 с.
3. Жевержеев В.Ф., Кальницкий Л.А., Сапогов Н.А. Специальный курс высшей математики для вузов. – М.: Высшая школа, 1970 – 416 с.
4. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисления. – М.: Наука, 1984 – 432 с.
5. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1989 – 656 с.
6. Мантуров О.В. Курс высшей математики. – М.: Высшая школа, 1996 – 448 с.
7. Рябушко А.П., Бархатов В.В., Державец В.В., Юруть И.Е. Сборник индивидуальных заданий по высшей математике. Ч. 2 – Мн.: Высшая школа, 1991. – 352 с.
Комплексные числа
Методические указания и индивидуальные задания по разделу «Комплексные числа» для студентов всех специальностей
очной формы обучения
Самара 2007
УДК 517
Высшая математика: методические указания и индивидуальные задания по разделу «Комплексные числа» для студентов всех специальностей очной формы обучения / составители: В.А. Паняев, Н.М. Латыпова. – Самара: СамГАПС, 2007. – 24 с.
Утверждено на заседание кафедры 03.10.2006, протокол №2.
Печатается по решению редакционно-издательского совета академии.
Методические указания и индивидуальные задания составлены в соответствии с Государственным образовательным стандартом и действующей программой по высшей математике для технических вузов.
Составители: к.т.н., доцент В.А. Паняев
к.ф.-м.н., доцент Н.М. Латыпова
Рецензенты: к.т.н., доцент СГАУ В.В. Максимов
к.ф.-м.н., доцент СамГАПС В.Л. Шур
Под редакцией составителей
Подписано в печать 19.04.2007. Формат 60  84 1/16.
84 1/16.
Бумага офсетная. Печать офсетная. Усл. п. л. 1,5.
Тираж 150 экз. Заказ № 68.
© Самарская государственная академия путей сообщения, 2007
Комплексные числа
Числовые множества и комплексные числа
История введения в математику понятия комплексного числа отражает общую тенденцию развития математических исчислений, когда использование новых математических операций приводило к необходимости расширения числовой области.
Понятие числа, являясь первичным и основным в математике, прошло, как известно, длительный путь исторического развития.
Множество натуральных чисел 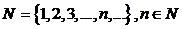 появилось в связи с необходимостью проводить счет (сложение и умножение) реальных предметов. Потребности практики и развитие математики привели к необходимости введения обратных операций – вычитания, деления и извлечения корня. Натуральный ряд был дополнен противоположными натуральным по значению отрицательными числами и нулем, что привело к возникновению множества целых чисел
появилось в связи с необходимостью проводить счет (сложение и умножение) реальных предметов. Потребности практики и развитие математики привели к необходимости введения обратных операций – вычитания, деления и извлечения корня. Натуральный ряд был дополнен противоположными натуральным по значению отрицательными числами и нулем, что привело к возникновению множества целых чисел 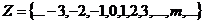 ,
, 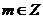 затем рациональных
затем рациональных 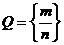 ,
, 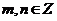 ,
,  и иррациональных
и иррациональных 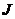 . Последние были введены в связи с необходимостью измерения отрезков, длина которых не является рациональным числом.
. Последние были введены в связи с необходимостью измерения отрезков, длина которых не является рациональным числом.
Операция извлечения корня явилась причиной введения общего понятия действительного числа. Как известно, множества рациональных и иррациональных чисел в совокупности образуют упорядоченное множество действительных чисел  , где
, где 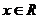 , т.е.
, т.е. 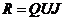 , и изображают точками непрерывной числовой оси
, и изображают точками непрерывной числовой оси 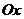 . С их помощью можно выразить длину любого реального отрезка.
. С их помощью можно выразить длину любого реального отрезка.
Для рассмотренных числовых множеств имеет место такое последовательное включение:
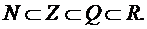
Понятие комплексного числа z представляет расширение понятия действительных чисел, которые можно рассматривать как некоторое подмножество в множестве комплексных чисел  , т.е.
, т.е. 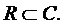
Исторически комплексные числа z обязаны своим возникновением попыткам найти решение алгебраических уравнений. Частные случай, связанный с необходимостью извлечения квадратного корня или корня четной степени из отрицательного числа привел к необходимости введения мнимых чисел, в отличие от действительных, и появлению множества комплексных чисел  .
.
В XVI веке в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных чисел. Рассмотрим решение простейшего кубического уравнения  :
:
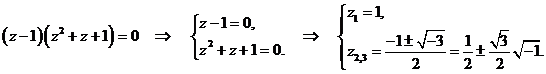 (1.1)
(1.1)
Чтобы объяснить парадокс – извлечение квадратного корня из отрицательного числа, итальянский ученый-алгебраист эпохи Возрождения Джироламо Кардано в 1545 г. предложил ввести в математические операции числа новой природы, назвав их «чисто отрицательными», однако считая их бесполезными для приложений. В 1572 г. итальянский алгебраист Раффаэле Бомбелли установил первые арифметические операции над такими числами.
Название «мнимые числа» ввел в 1637 г. французский математик и философ Рэне Декарт. В 1777 г. один из крупнейших математиков XVIII века Леонард Эйлер для обозначения 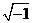 предложил использовать первую букву французского слова
предложил использовать первую букву французского слова 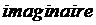 (мнимый, воображаемый, несуществующий), т.е. ввести обозначение
(мнимый, воображаемый, несуществующий), т.е. ввести обозначение  в структуру комплексных чисел. Тогда корни z2,3 выше приведенного кубического уравнения записываются в виде
в структуру комплексных чисел. Тогда корни z2,3 выше приведенного кубического уравнения записываются в виде
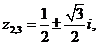 (1.2)
(1.2)
т.е. в алгебраической форме комплексное число принимает вид 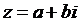 , где a и b – действительные числа,
, где a и b – действительные числа,  мнимая единица.
мнимая единица.
Общая теория корней n -й степени из отрицательных и любых комплексных чисел основана на формуле английского математика французского происхождения Абрахама де Муавра, и была построена на рубеже XVII – XVIII веков.
В конце XVIII – начале XIX века было получено геометрическое истолкование комплексных чисел. Независимо друг от друга датчанин Каспар Вессель, француз Жан Аргон и крупнейший немецкий математик Карл Гаусс предложил изображать комплексное число точкой М(а, b) на координатной комплексной плоскости. Позднее пришли к выводу, что такое число удобнее изображать не самой точкой, а радиусом-вектором  , проведенным в точку М из начала координат, что позволило рассматривать операции сложения и вычитания комплексных чисел как операции над соответствующими векторами.
, проведенным в точку М из начала координат, что позволило рассматривать операции сложения и вычитания комплексных чисел как операции над соответствующими векторами.
Геометрический подход к изображению комплексных чисел и накопленные знания об их свойствах создали предпосылки для разработки теории функций комплексной переменной. Комплексные числа в настоящее время находят широкое применение в различных областях науки и техники: при расчетах электрических цепей, решении обыкновенных дифференциальных уравнений и дифференциальных уравнений математической физики, при изучении течения жидкостей и газа (аэро и гидродинамика), решении задач теории упругости, проблем квантовой теории поля и многих других задач.
2. Различные формы представления комплексных чисел и операции над ними
Для каждого комплексного числа возможны три формы его представления: алгебраическая, тригонометрическая и показательная формы. В зависимости от конкретного случая и проводимых операций над комплексными числами используется та или иная форма. При необходимости всегда возможен переход из одной формы комплексного числа в другую.
Рассмотрим каждую из этих форм отдельно.
2.1. Алгебраическая форма комплексного числа. Рациональные действия над комплексными числами
Множество, состоящее из выражений вида
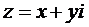 , (2.1)
, (2.1)
где 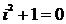 , а
, а 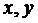 - действительные числа, называется множеством комплексных чисел, представленных в алгебраической форме*.
- действительные числа, называется множеством комплексных чисел, представленных в алгебраической форме*.
Числа х и y называются соответственно действительной и мнимой частями комплексного числа 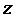 и обозначаются
и обозначаются 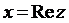 ,
, 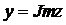 ;
;  - мнимая единица (i 2= -1).
- мнимая единица (i 2= -1).
При  комплексное число
комплексное число 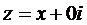 совпадает с действительным числом х; если
совпадает с действительным числом х; если  , то имеем комплексное число
, то имеем комплексное число 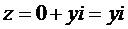 , которое называется чисто мнимым. Отождествляя комплексные числа вида
, которое называется чисто мнимым. Отождествляя комплексные числа вида 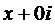 с действительными числами х, убеждаемся в том, что действительные числа являются частным случаем комплексных чисел z (подмножеством
с действительными числами х, убеждаемся в том, что действительные числа являются частным случаем комплексных чисел z (подмножеством  множества комплексных чисел
множества комплексных чисел  , т.е.
, т.е. 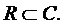 )
)
Два комплексных числа 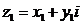 и
и 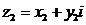 считаются равными только в том случае, если их действительные и мнимые части соответственно равны:
считаются равными только в том случае, если их действительные и мнимые части соответственно равны:
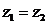 , если
, если 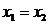 и
и 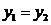 .
.
В противном случае 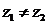 . Отношений
. Отношений 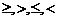 для комплексных чисел не существует.
для комплексных чисел не существует.
Комплексное число равно нулю только в том случае, если равны нулю его действительная и мнимая части:
 , если
, если 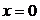 и
и 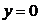 .
.
Числа вида  и
и 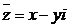 , являющиеся корнями квадратного уравнения с отрицательным дискриминантом (
, являющиеся корнями квадратного уравнения с отрицательным дискриминантом ( , см. решение кубического уравнения
, см. решение кубического уравнения  ), называются комплексно-сопряженными числами.
), называются комплексно-сопряженными числами.
* Общепринятой является u форма записи комплексного числа  , где a и b – действительные числа, о чем говорилось ранее.
, где a и b – действительные числа, о чем говорилось ранее.
Операции сложения, вычитания, умножения и деления над комплексными числами 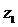 и
и  производятся как над алгебраическими двучленами, принимая во внимание, что
производятся как над алгебраическими двучленами, принимая во внимание, что 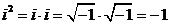 :
:
1) 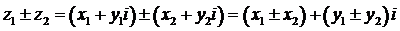 ; (2.2)
; (2.2)
2) 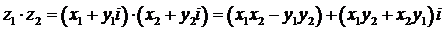 . (2.3)
. (2.3)
3) При делении комплексных чисел «уничтожается мнимость в знаменателе», для чего умножают числитель и знаменатель на число, комплексно-сопряженное знаменателю:
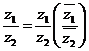 , где
, где 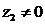 , (2.4)
, (2.4)
или 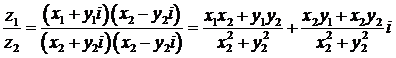 . (2.5)
. (2.5)
Рассмотренные операции над комплексными числами обладают всеми свойствами соответствующих операций над действительными числами.
4) Сумма и произведение комплексно-сопряженных чисел  и
и 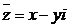 есть всегда действительное число, в чем нетрудно убедиться:
есть всегда действительное число, в чем нетрудно убедиться:
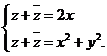 (2.6)
(2.6)
5) Для комплексных чисел остаются верными также алгебраические формулы сокращенного умножения:
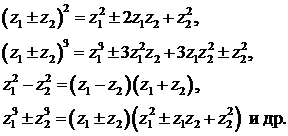 (2.7)
(2.7)
Примеры.
1. 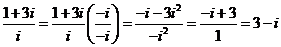 .
.
2. 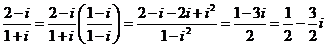 .
.



 84 1/16.
84 1/16.
 удобно изображать точкой
удобно изображать точкой  на комплексной плоскости
на комплексной плоскости 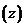 (рис. 1). Оси
(рис. 1). Оси 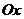 и
и 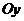 прямоугольной декартовой системы координат на этой плоскости называются соответственно действительной и мнимой осями. Между точками плоскости
прямоугольной декартовой системы координат на этой плоскости называются соответственно действительной и мнимой осями. Между точками плоскости  и изображенными на ней комплексными числами существует взаимно однозначное соответствие.
и изображенными на ней комплексными числами существует взаимно однозначное соответствие.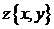 с началом в начале системы координат и концом в этой точке, проекции которого на оси координат будут соответственно х и y. Длина (модуль) этого вектора
с началом в начале системы координат и концом в этой точке, проекции которого на оси координат будут соответственно х и y. Длина (модуль) этого вектора . (2.8)
. (2.8)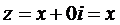 изображаются на комплексной плоскости точками (х, о) оси
изображаются на комплексной плоскости точками (х, о) оси 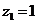 будет являться единичным вектором оси
будет являться единичным вектором оси 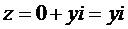 будут соответствовать точки
будут соответствовать точки  оси
оси  изображается точкой (0, 1) мнимой оси и одновременно являться единичным вектором
изображается точкой (0, 1) мнимой оси и одновременно являться единичным вектором 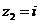 оси
оси  на комплексной плоскости изображается векторами
на комплексной плоскости изображается векторами 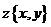 и
и  , симметричными действительной оси
, симметричными действительной оси 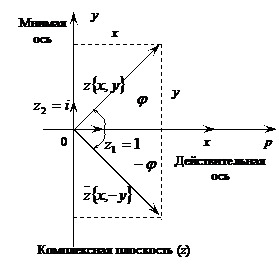

 , что используется при анализе различных функций комплексной переменной и графическом изображении области их определения.
, что используется при анализе различных функций комплексной переменной и графическом изображении области их определения.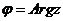 . Угол
. Угол 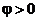 , если отсчет его производится против направления движения часовой стрелки, и
, если отсчет его производится против направления движения часовой стрелки, и 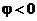 , если по часовой стрелке. Очевидно, что для всякого комплексного числа
, если по часовой стрелке. Очевидно, что для всякого комплексного числа 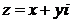 справедливы формулы:
справедливы формулы: ;
; 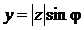 ;
; ;
; 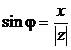 ;
; 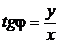 ; (2.9)
; (2.9)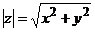 ,
,  .
.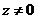 может иметь бесконечное множество значений, отличающихся одно от другого на слагаемое кратное
может иметь бесконечное множество значений, отличающихся одно от другого на слагаемое кратное 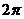 . Поэтому условия равенства комплексных чисел заключается в том, что длины (модули) должны быть равны, а аргументы φ могут отличаться на величины, кратные
. Поэтому условия равенства комплексных чисел заключается в том, что длины (модули) должны быть равны, а аргументы φ могут отличаться на величины, кратные  ,которое обозначают а rgz. Оно называется главным значением аргумента комплексного числа:
,которое обозначают а rgz. Оно называется главным значением аргумента комплексного числа: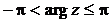 или
или  . (2.10)
. (2.10)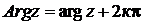 , где
, где 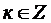 . (2.11)
. (2.11)
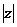 и углы
и углы  является полярными координатами точки z, т.е.
является полярными координатами точки z, т.е. 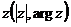 .
. . (2.13)
. (2.13) , т.к.
, т.к. 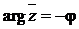 , выражается формулой
, выражается формулой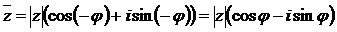 (2.14)
(2.14)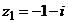 и
и 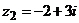 на комплексной плоскости и записать их в тригонометрической форме.
на комплексной плоскости и записать их в тригонометрической форме.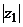 и
и 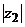 и главные аргументы
и главные аргументы  и
и 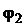 (рис. 3).
(рис. 3).
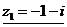
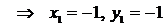 ,
,  .
.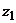 или его вектор
или его вектор  находятся в III четверти. Используя формулу (2.12) для этой четверти, имеем
находятся в III четверти. Используя формулу (2.12) для этой четверти, имеем , или
, или 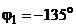 .
.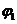 , показанным на рис. 3, тогда
, показанным на рис. 3, тогда 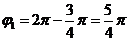 или
или 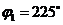 . Тригонометрическая форма числа
. Тригонометрическая форма числа  или
или 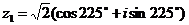 .
.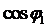 и
и 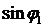 , придем к исходной алгебраической форме этого числа
, придем к исходной алгебраической форме этого числа 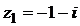 .
. ,
, 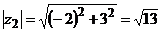 .
.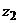 и его вектор
и его вектор 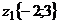 находятся во II четверти. На основании формулы (2.12) получим
находятся во II четверти. На основании формулы (2.12) получим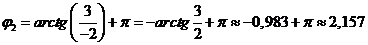 рад, или
рад, или 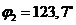 ;
; или
или 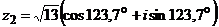 .
.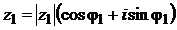 ,
,  .
.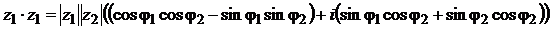 .
.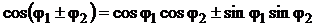 и
и 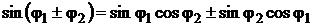 , окончательно получим:
, окончательно получим: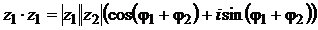 . (2.15)
. (2.15)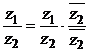 , то подставляя в это выражение
, то подставляя в это выражение 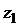 ,
, 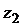 и
и 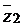 в тригонометрической форме и проводя соответствующие преобразования получим:
в тригонометрической форме и проводя соответствующие преобразования получим: .
.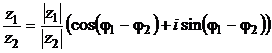 . (2.16)
. (2.16)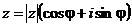 в натуральную степень n, принимая во внимание, что
в натуральную степень n, принимая во внимание, что 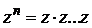 . (n раз).
. (n раз).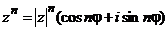 . (2.17)
. (2.17)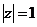 формула (2.16) принимает вид
формула (2.16) принимает вид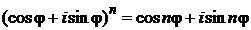 . (2.18)
. (2.18)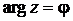 .
.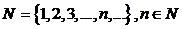 появилось в связи с необходимостью проводить счет (сложение и умножение) реальных предметов. Потребности практики и развитие математики привели к необходимости введения обратных операций – вычитания, деления и извлечения корня. Натуральный ряд был дополнен противоположными натуральным по значению отрицательными числами и нулем, что привело к возникновению множества целых чисел
появилось в связи с необходимостью проводить счет (сложение и умножение) реальных предметов. Потребности практики и развитие математики привели к необходимости введения обратных операций – вычитания, деления и извлечения корня. Натуральный ряд был дополнен противоположными натуральным по значению отрицательными числами и нулем, что привело к возникновению множества целых чисел 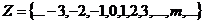 ,
, 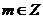 затем рациональных
затем рациональных 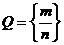 ,
, 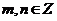 ,
,  и иррациональных
и иррациональных 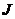 . Последние были введены в связи с необходимостью измерения отрезков, длина которых не является рациональным числом.
. Последние были введены в связи с необходимостью измерения отрезков, длина которых не является рациональным числом. , где
, где 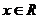 , т.е.
, т.е. 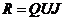 , и изображают точками непрерывной числовой оси
, и изображают точками непрерывной числовой оси 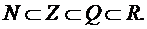
 , т.е.
, т.е. 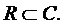
 :
: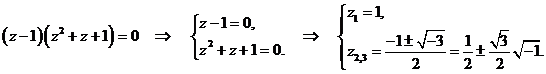 (1.1)
(1.1)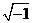 предложил использовать первую букву французского слова
предложил использовать первую букву французского слова 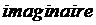 (мнимый, воображаемый, несуществующий), т.е. ввести обозначение
(мнимый, воображаемый, несуществующий), т.е. ввести обозначение  в структуру комплексных чисел. Тогда корни z2,3 выше приведенного кубического уравнения записываются в виде
в структуру комплексных чисел. Тогда корни z2,3 выше приведенного кубического уравнения записываются в виде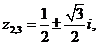 (1.2)
(1.2)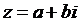 , где a и b – действительные числа,
, где a и b – действительные числа,  мнимая единица.
мнимая единица. , проведенным в точку М из начала координат, что позволило рассматривать операции сложения и вычитания комплексных чисел как операции над соответствующими векторами.
, проведенным в точку М из начала координат, что позволило рассматривать операции сложения и вычитания комплексных чисел как операции над соответствующими векторами.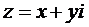 , (2.1)
, (2.1)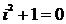 , а
, а 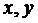 - действительные числа, называется множеством комплексных чисел, представленных в алгебраической форме*.
- действительные числа, называется множеством комплексных чисел, представленных в алгебраической форме*.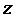 и обозначаются
и обозначаются 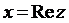 ,
, 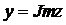 ;
;  комплексное число
комплексное число 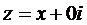 совпадает с действительным числом х; если
совпадает с действительным числом х; если  , то имеем комплексное число
, то имеем комплексное число 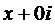 с действительными числами х, убеждаемся в том, что действительные числа являются частным случаем комплексных чисел z (подмножеством
с действительными числами х, убеждаемся в том, что действительные числа являются частным случаем комплексных чисел z (подмножеством 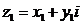 и
и 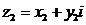 считаются равными только в том случае, если их действительные и мнимые части соответственно равны:
считаются равными только в том случае, если их действительные и мнимые части соответственно равны: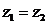 , если
, если 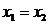 и
и 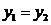 .
.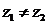 . Отношений
. Отношений 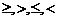 для комплексных чисел не существует.
для комплексных чисел не существует. , если
, если 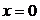 и
и 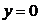 .
.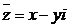 , являющиеся корнями квадратного уравнения с отрицательным дискриминантом (
, являющиеся корнями квадратного уравнения с отрицательным дискриминантом ( , см. решение кубического уравнения
, см. решение кубического уравнения  , где a и b – действительные числа, о чем говорилось ранее.
, где a и b – действительные числа, о чем говорилось ранее.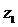 и
и  производятся как над алгебраическими двучленами, принимая во внимание, что
производятся как над алгебраическими двучленами, принимая во внимание, что 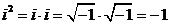 :
: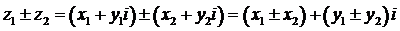 ; (2.2)
; (2.2)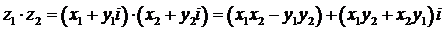 . (2.3)
. (2.3)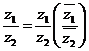 , где
, где 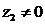 , (2.4)
, (2.4)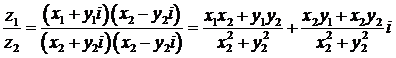 . (2.5)
. (2.5)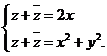 (2.6)
(2.6)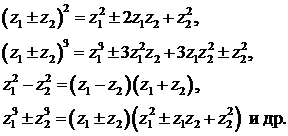 (2.7)
(2.7)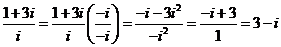 .
.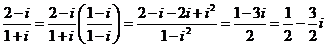 .
.


