Выходит из закона сохранения энергии. Включает в себя внутреннюю энергию и кинетическую энергию в макродвижениях
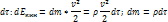
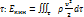 (4.1)
(4.1)
С точки зрения физики в внутреннюю энергию следует включить:
1)кинетическую энергию хаотического поступательного движения молекул.
2)кинетическую энергию хаотического вращательного движения молекул.
3)кинетическую энергию колебательного движения в молекулах.
4)энергию связей атомом в молекулах.(энергия диссоциации)
5)энергию связи электронной оболочки с ядром атома.(энергия ионизации)
6)энергию связи элементарной частицы в ядре атома
7)энергию потенциального взаимодействия между молекулами.
8)энергию взаимодействия с другими телами.
С точки зрения МЖГ во внутреннюю энергию следует включить лишь те состояния, которые изменяются с течением времени.
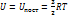 , Т – энергия единицы массы. R – газовая постоянная сорта газа.
, Т – энергия единицы массы. R – газовая постоянная сорта газа.
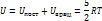
 (4.2)
(4.2)

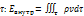 (4.3)
(4.3)
12. Вектор 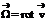 и его компоненты в декартовых координатах. Связь
и его компоненты в декартовых координатах. Связь 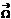 с угловой скоростью вращения жидкой частицы.
с угловой скоростью вращения жидкой частицы.
Скорость любой точки жидкой частицы может быть представлена в виде
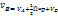
Где  - скорость полюса,
- скорость полюса,  - чисто деформационная скорость,
- чисто деформационная скорость, 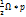 -скорость точки во вращательном движении затвердевшей жидкой частицы с угловой скоростью
-скорость точки во вращательном движении затвердевшей жидкой частицы с угловой скоростью 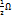 .
.
Вектор Ω= rotv=2ω- удвоенная угловая скорость, с которой затвердевшая жидкая частица вращается вокруг оси, проходящей через полюс. Проекция вихря скорости
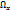 =
= 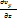 -
- 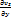 = 2
= 2 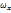 ,
,
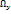 =
= 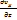 -
- 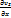 = 2
= 2 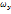 ,
,
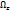 =
= 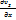 -
- 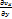 = 2
= 2 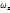 .
.
Проекцию вектора угловой скорости на какую-либо ось можно одновременно рассматривать как угловую скорость вращения относительно этой оси. Поэтому проекция вихря скорости есть удвоенные угловые скорости, с которыми затвердевшая жидкая частица вращается вокруг осей, параллельных осям координат.
Теорема Гельмгольца.
Составим ряд Тейлора для скорости в точке М.
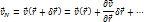
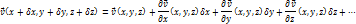
Проекции скоростей на оси.
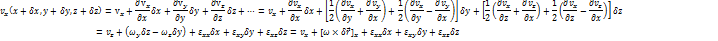
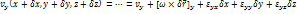
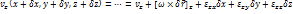
Введем в рассмотрение матрицу E.
 (5.6)
(5.6)
Полученное соотношение 5.6 представляет собой теорему Гельмгольца.
15. Модель вязкой ньютоновской жидкости (газа) (определение, свойства, происхождение, физический смысл коэффициентов в выражении тензора напряжений через тензор скоростей деформаций).
Реологические модели в МЖГ. Реологической моделью называют зависимость тензора напряжений в среде от термодинамических и деформационных параметров среды.
Рассмотрим в МЖГ 2 реологические модели:
1. Модель идеальной жидкости
2. Модель вязкой ньютоновской жидкости(является более общей включает в себя первую как частный случай).
Рассмотрим 2 модель, а потом 1, как частный случай.
Модель вязкой ньютоновской жидкости – среда, для которой выполняются следующие соотношения для тензора напряжений:
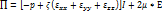 (6.1)
(6.1)
E – Тензор скоростей.
I – Единичный тензор.
P – Давление.
Ϛ – Коэффициент объемной вязкости.
μ – Коэффициент динамической вязкости.
 (6.2)
(6.2)
Существует 3 свойства модели вязкой ньютоновской жидкости:
1)Коэф-ты р, Ϛ, μ – скалярны. Значение не зависит от выбора системы координат, с точки зрения матаематики. С точки зрения МЖГ означает, что изотропичность (одинаковость по всем направлениям) реологических свойств среды.
2)Зависимость компонент тензора напряжений 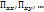 от компонент тензора скоростей деформации
от компонент тензора скоростей деформации 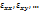 является линейной(свойство можно проследить из формулы 6.2)
является линейной(свойство можно проследить из формулы 6.2)
 3)Если жидкость неподвижна или движется как абсолютно твердое тело, то в ней действуют только нормальные напряжения.
3)Если жидкость неподвижна или движется как абсолютно твердое тело, то в ней действуют только нормальные напряжения.
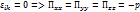 , остальные
, остальные 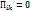 Нормальные напряжения в этом случае не зависят от ориентировки площадки.
Нормальные напряжения в этом случае не зависят от ориентировки площадки.
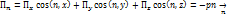
 (2.8)
(2.8) 
(2.10) 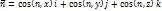
О происхождении модели в формуле 6.1.
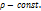 (1.8)
(1.8)
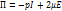 (6.3) Формула Стокса(1845 г.)
(6.3) Формула Стокса(1845 г.)
Соотношение 6.1(как и 6.3) является интеллектуальным обобщением огромного количества наблюдений и измерений.
Физический смысл
В главных осях тензора скоростей деформаций касательные напряжения в вязкой жидкости равны нулю. Но такие оси есть главные оси тензора напряжений. Следовательно, главные оси тензора скоростей деформаций одновременно являются и главными осями тензора напряжений.
Выражения для компонент тензора напряжений в вязкой ньютоновской среде (в сжимаемом газе и несжимаемой жидкости). Тензор вязких напряжений (выражения его диагональных и недиагональных компонент через компоненты тензора скоростей деформаций). Коэффициент динамической вязкости (размерность, зависимость от температуры для газов и жидкостей).
Выражения для компонент тензора напряжений.
Выражения для компонент тензора напряжений в вязкой ньютоновской среде (в сжимаемом газе и несжимаемой жидкости).
 (6.8)
(6.8)
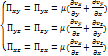 (6.9)
(6.9)
Пусть 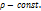
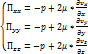 (6.10)
(6.10)
Наряду с 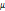 для несжимаемой жидкости часто рассматривают величину ν, называемую кинематическим коэффициентом вязкости
для несжимаемой жидкости часто рассматривают величину ν, называемую кинематическим коэффициентом вязкости 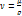 . Коэффициент
. Коэффициент 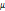 может быть определен экспериментально; в случае, если известен закон межмолекулярного воздействия, его можно вычислить теоретически. Вообще говоря,
может быть определен экспериментально; в случае, если известен закон межмолекулярного воздействия, его можно вычислить теоретически. Вообще говоря, 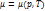 , но зависимость от давления слабая.
, но зависимость от давления слабая.
Тензор вязких напряжений (выражения его диагональных и недиагональных компонент через компоненты тензора скоростей деформаций).
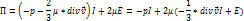
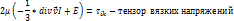
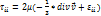 (6.11)
(6.11)
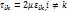
Физический смысл динамического коэффициента вязкости заключается в том, что он численно равен касательному напряжению, возникающему между слоями жидкости, движущимися друг относительно друга со скоростью, равной единице, при расстоянии между этими слоями, равном единице длины.
В отличие от жидкостей, вязкость газов увеличивается с увеличением температуры (у жидкостей она уменьшается при увеличении температуры).
Формула Сазерленда может быть использована для определения вязкости идеального газа в зависимости от температуры:
 (6.4)
(6.4)
Для жидкостей:
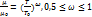 (6.5)
(6.5)
Размерность динамического коэффициента вязкости h в системе СИ есть Па×с:
1 Па×с = 1 кг/(м с)
17. Модель идеальной жидкости (газа) (определение, выражения для компонент тензора напряжений, уравнения количества движения и энергии).
Идеальная жидкость(газ) называется среда(в которой отсутствуют вязкость и теплопроводность. Так как в ней отсутствует внутреннее трение, то нет касательных напряжений между двумя соседними слоями жидкости.), и в которой тензор напряжений равен:
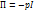 (6.12)
(6.12)
Идеальный газ, - у которого отсутствуют силы взаимодействия между молекулами, а размеры молекул много меньше межмолекулярных расстояний.
Ур-е состояния ид.газа - PV=RT
Выражения для компонент тензора напряжений в вязкой ньютоновской среде (в сжимаемом газе и несжимаемой жидкости).  (6.8)
(6.8) 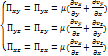 (6.9)
(6.9)
Уравнение кол-ва движения для стационарного потока(одномерного): 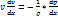
В этой форме уравнение часто используется для решения различных прикладных задач гидродинамики и газодинамики. В частности, интегрированием этого уравнения по x при постоянной плотности жидкости  получается известное уравнение Бернулли для несжимаемой жидкости:
получается известное уравнение Бернулли для несжимаемой жидкости: 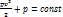
Уравнение количества движения в дифференциальной форме.
Применяя формулу Остроградского-Гаусса, преобразовываем интеграл Коши по площади к объему. 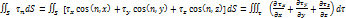
Получаем интегральную запись закона в виде
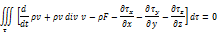
Так как интегральная форма имеет место для любого объема 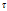 , то, следовательно
, то, следовательно
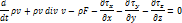
Выполнив дифференцирование в первом слагаемом, можем переписать это в виде:
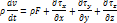
Или в проекциях на оси координат:
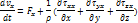
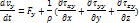
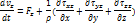
Слева в уравнениях проекция на оси стоит оператор полной производной. Эти уравнения называют уравнениями движения сплошной среды в напряжениях.
Уравнения энергии
Выходит из закона сохранения энергии. Включает в себя внутреннюю энергию и кинетическую энергию в макродвижениях.
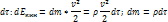
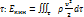 (4.1)
(4.1)
С точки зрения физики в внутреннюю энергию следует включить:
1)кинетическую энергию хаотического поступательного движения молекул.
2)кинетическую энергию хаотического вращательного движения молекул.
3)кинетическую энергию колебательного движения в молекулах.
4)энергию связей атомом в молекулах.(энергия диссоциации)
5)энергию связи электронной оболочки с ядром атома.(энергия ионизации)
6)энергию связи элементарной частицы в ядре атома
7)энергию потенциального взаимодействия между молекулами.
8)энергию взаимодействия с другими телами.
С точки зрения МЖГ во внутреннюю энергию следует включить лишь те состояния, которые изменяются с течением времени.
Из молекулярной физики нам известно, что внутренняя энергия одноатомного газа равна:
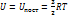 , Т – энергия единицы массы. R – газовая постоянная сорта газа.
, Т – энергия единицы массы. R – газовая постоянная сорта газа.
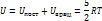
 (4.2)
(4.2)

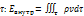 (4.3)
(4.3)
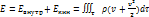 (4.4)
(4.4)
Во время движения полного жидкого объема, его полная энергия в общем случае будет меняться.
1)Работа внешних сил, приложенных к 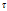
2)Работа поверхностных сил, приложенных к 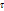 , со стороны жидкости вне
, со стороны жидкости вне  .
.
3)Подвод тепла к  за счет механизма объемного поглощения тепла.
за счет механизма объемного поглощения тепла.
4)Подвод тепла к  через плоскость S.
через плоскость S.
Вектор плотности потока тепла (определение, физические причины теплопроводности в жидкостях и газах). Закон Фурье (математическое выражение, размерность коэффициента теплопроводности и его зависимость от температуры для газов и жидкостей).
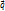 - направление в сторону теплового потока. Кол-во тепла, проходящее через единичную площадь. Тепло в жидкостях может передаваться за счет 2х существенно разных механизмов:
- направление в сторону теплового потока. Кол-во тепла, проходящее через единичную площадь. Тепло в жидкостях может передаваться за счет 2х существенно разных механизмов:
1) Молекулярная диффузия
2) Молекулярная теплопроводность
В обычных условиях механизмы теплопроводности существенно доминируют над диффузией так, что последнее не играет роли. Молекулярная теплопроводность хорошо описывается законом Фурье. Минус в правой части показывает, что тепловой поток направлен противоположно вектору grad T (то есть в сторону скорейшего убывания температуры). Это выражение известно как закон теплопроводности Фурье:
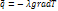 , коэф-т теплопроводности Дж/(м*с*К)(7.1)
, коэф-т теплопроводности Дж/(м*с*К)(7.1)
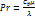 (7.2) число Прандтля
(7.2) число Прандтля
Prandtl: 150K<T<1200K
Pr - const.
150K≤T≤700K
Cp ≈ const
 (7.3)
(7.3)
Коэффициент теплопроводности газов возрастает с увеличением температуры и составляет 0,006÷0,6 Вт/(м·К). Следует отметить, что верхнее значение относится к гелию и водороду, коэффициент теплопроводности которых в 5—10 раз больше, чем у других газов. Коэффициент теплопроводности воздуха при 0 0С равен 0,0244 Вт/(м·К). Для жидкости λ =0,07÷0,7 Вт/(м·К) и, как правило, уменьшается с увеличением температуры. Коэффициент теплопроводности воды с увеличением температуры возрастает до максимального значения 0,7 Вт/(м·К) при t=120 0С и дальше уменьшается. Наилучшими проводниками теплоты являются металлы, у которых λ =20÷418 Вт/(м·К). Самый теплопроводный металл — серебро. Для большинства металлов коэффициент теплопроводности убывает с возрастанием температуры, а также при наличии разного рода примесей. Поэтому коэффициент теплопроводности легированных сталей значительно ниже, чем чистого железа.
Билет № 26 Уравнение Бернулли для несжимаемой жидкости в поле сил тяжести (получение уравнения, физическая интерпретация слагаемых). Истечение жидкости из сосуда через малое отверстие (задача Торичелли).
Уравнение Бернулли для несжимаемой жидкости. В этом случаи ρ-заданная постоянная и 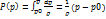 .
.
Интеграл Бернулли примет вид 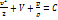 (2.12)
(2.12)
Если массовые силы – силы тяжести, то V=gz и интеграл Бернулли в этом случае
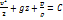 (2.13) или
(2.13) или 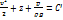 (2.14)
(2.14)
Отдельные слагаемые в (2.14) имеют размерность длины и называются соответственно: 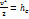 – скоростной, z – геометрической,
– скоростной, z – геометрической, 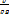 - пьезометрической высотами. Равенство (2.14) позволяет дать такую формулировку интеграла Бернулли: при движении однородной несжимаемой жидкости в поле сил тяжести сумма скоростной, пьезометрической и геометрической высот постоянна вдоль линии тока.
- пьезометрической высотами. Равенство (2.14) позволяет дать такую формулировку интеграла Бернулли: при движении однородной несжимаемой жидкости в поле сил тяжести сумма скоростной, пьезометрической и геометрической высот постоянна вдоль линии тока.
Истечение жидкости из сосуда через малое отверстие. Рассмотрим истечение жидкости из сосуда через отверстия. Будем считать, что отверстие расположено в близи дна. Жидкость предположим несжимаемой и находящийся в поле сил тяжести. Пусть S – площадь открытой поверхности жидкости в сосуде, s – площадь отверстия, H – уровень жидкости в сосуде.
Предполагаем, что s/S<< 1. Когда отверстие открыто, то уровень в сосуде понижается, хотя и медленно. Возникающее течение будет неустановившемся, но медленно изменяющемся во времени (s/S мало). Это движение можно приближенно рассматривать как последовательную смену установившихся движений. Такая трактовка неустановившихся движений носит название квазистационарной трактовки, или квазистационарного подхода. При таком подходе можем записать интеграл Бернулли, который для несжимаемой жидкости при V = gz для любой линии тока имеет вид (2.13).
Рассмотрим линию тока AB, проходящую через точку A поверхности S и точку B в сечение s. Записав интеграл Бернулли для точек A и B этой линии, будем иметь 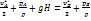
Принимая, что давление в точках A и B равно атмосферному 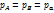 , получаем
, получаем 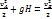
Уравнение неразрывности (постоянство расхода) приводит к соотношению
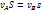
Из последних двух равенств найдем скорость истечения жидкости из сосуда 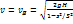
Так как s/S<< 1, то можно написать 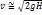
Последняя формула есть известная формула Торричелли. Скорость истечения не отличается от скорости материальной точки, падающей с высоты H.
Билет №12 Вектор 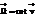 и его компоненты в декартовых координатах. Связь
и его компоненты в декартовых координатах. Связь  с угловой скоростью вращения жидкой частицы.
с угловой скоростью вращения жидкой частицы.
Вектор 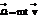 и его компоненты в декартовых координатах. Связь
и его компоненты в декартовых координатах. Связь 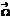 с угловой скоростью вращения жидкой частицы.
с угловой скоростью вращения жидкой частицы.
Уравнение Эйлера в форме Громеки – Лэмба: 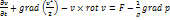
Запишем уравнение в проекции на оси, используя обозначение 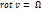 :
:

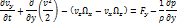
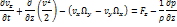
Здесь 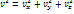
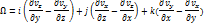
Уравнение Громеки – Лэмба содержат в явном виде вектор вихря Ω.
Компоненты скорости есть частные производные от φ(x,y,z,t) по координатам. Функцию φназывают потенциалом скоростей.
Билет №27 Уравнение Бернулли для совершенного газа (получение уравнения из общего интеграла Бернулли, переход к различным формам записи уравнения: через энтальпию, внутреннюю энергию, температуру). Уравнение Бернулли для несжимаемого газа (сравнение со случаем совершенного газа). Определение скорости потока несжимаемого газа с помощью трубки Пито–Прандтля.
Уравнение Бернулли для совершенного газа. В термодинамике энтальпия единицы массы газа определяется выражением 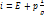 (3.1). Следовательно, при малых изменениях параметра состояния
(3.1). Следовательно, при малых изменениях параметра состояния 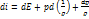
На основание первого начала термодинамике сумма 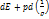 равна притоку тепла dq к системе. Если приток тепла к системе или отвод тепла от нее отсутствует, т.е. если процесс адиабатический, то dq=0 и
равна притоку тепла dq к системе. Если приток тепла к системе или отвод тепла от нее отсутствует, т.е. если процесс адиабатический, то dq=0 и 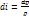 . Таким образом, адиабатического процесса равенство
. Таким образом, адиабатического процесса равенство 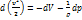 (при отсутствие массовых сил) можно записать в виде
(при отсутствие массовых сил) можно записать в виде 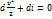 и соответственно интеграл Бернулли – в виде
и соответственно интеграл Бернулли – в виде 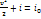 (3.2), где
(3.2), где  - значение энтальпии при v = 0.
- значение энтальпии при v = 0.
Если ввести в (3.2) выражение (3.1) для i, то будем иметь 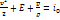
Здесь E – внутренняя энергия, складывающаяся в случае многоатомного газа из энергии поступательного 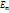 , вращательного
, вращательного 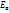 и колебательного
и колебательного 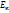 движения молекул(предполагается, что нет процессов диссоциации, ионизации и др.). В газовой динамике предполагают, что газ совершенный, а теплоемкость обычно считают постоянной, что справедливо в определенном диапазоне температуры, когда можно не учитывать колебательную энергию. В этом случае для двух атомных газов (воздух обычно рассматривают как смесь кислорода и азота)
движения молекул(предполагается, что нет процессов диссоциации, ионизации и др.). В газовой динамике предполагают, что газ совершенный, а теплоемкость обычно считают постоянной, что справедливо в определенном диапазоне температуры, когда можно не учитывать колебательную энергию. В этом случае для двух атомных газов (воздух обычно рассматривают как смесь кислорода и азота) 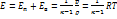 и энтальпия дается формулой
и энтальпия дается формулой 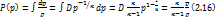 , а интеграл Бернулли имеет вид
, а интеграл Бернулли имеет вид 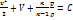 (2.17) при (V = 0). Если температуры таковы, что возбуждается и колебательная энергия
(2.17) при (V = 0). Если температуры таковы, что возбуждается и колебательная энергия 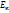 , то интеграл Бернулли надо писать в виде
, то интеграл Бернулли надо писать в виде 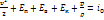
Для газа, находящегося в состоянии термодинамического равновесия, колебательная энергия есть функция температуры T, но при этом теплоемкость колебательных степеней свободы, а следовательно, и 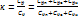 зависит от T.
зависит от T.
Выражение колебательной энергии для двухатомного газа 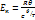 . Величина θ называется характеристическая температура
. Величина θ называется характеристическая температура  , где v – частота колебаний, h – постоянная Планка, а κ – постоянная Больцмана.
, где v – частота колебаний, h – постоянная Планка, а κ – постоянная Больцмана.
Интеграл Бернулли будет иметь вид 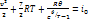
Уравнение Бернулли для несжимаемого газа. Пусть AB – линия тока, соединяющая точку A внутри сосуда с точкой B в сечение вытекающей струн. Для точек A и B можно записать адиабату Пуассона  (1.11) и интеграл Бернулли
(1.11) и интеграл Бернулли 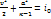 (2.19):
(2.19):
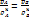 (4.1)
(4.1)

При большом сосуде и малом отверстии 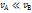 и можно принять
и можно принять  . Обозначая
. Обозначая 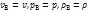 получаем из интеграла Бернулли (4.1)
получаем из интеграла Бернулли (4.1)
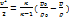 (4.2)
(4.2)
Определение скорости потока несжимаемого газа с помощью трубки Пито–Прандтля. 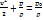
Отсюда 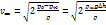
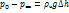
Билет 3 Понятие жидкого объема. Вывод формул для вычисления производной по времени от интеграла по жидкому объему.
Выделим некоторую массу жидкости, и пусть она в некоторый момент времени t занимает объем 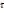 , ограниченный поверхностью S. Пусть в каждой точке (частице) этого объёма определена некоторая гидродинамическая величина A(скалярная, векторная или тензорная – безразлично). Рассмотрим интеграл.
, ограниченный поверхностью S. Пусть в каждой точке (частице) этого объёма определена некоторая гидродинамическая величина A(скалярная, векторная или тензорная – безразлично). Рассмотрим интеграл. 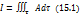
При перемещении выделенной массы жидкости будут изменяться положение её частиц, общий объём 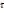 и значение величины A в различных точках. Интеграл есть функция времени
и значение величины A в различных точках. Интеграл есть функция времени 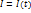 .
. 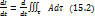
Получим выражение для производной 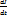 в переменных Эйлера и переменных Лагранжа.
в переменных Эйлера и переменных Лагранжа.
1.Вычисление 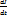 в переменных Эйлера. Рассмотрим два близких момента времени t и t’=t+
в переменных Эйлера. Рассмотрим два близких момента времени t и t’=t+ 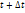 . Для момента времени t сохраним введённые обозначения: A(x,y,z,t)=A
. Для момента времени t сохраним введённые обозначения: A(x,y,z,t)=A 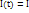 . Значение всех функций в момент t’=t+
. Значение всех функций в момент t’=t+ 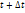 . Будем отмечать штрихами. Таким образом,
. Будем отмечать штрихами. Таким образом, 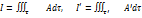
При малых 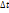 можем записать
можем записать
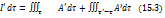 ->
-> 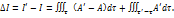
Подынтегральная функция A’-Aвычесляется в точках, принадлежащих объему 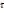 , но А вычисляется в момент t, а A’ – в момент t’=
, но А вычисляется в момент t, а A’ – в момент t’= 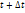 . С точночтьюдо малых более высокого порядка
. С точночтьюдо малых более высокого порядка 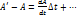
Учитывая это, приходим к равенству 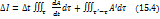
Преобразуем второе слагаемое.
Элемент 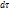 объёма
объёма 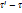 выберем в виде
выберем в виде 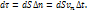 Тогда
Тогда
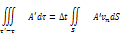
Равенство (15.4) можно тепрь записать в виде 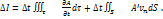
Разделим обе части на 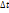 и устремим
и устремим 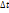 к нулю. При этом A’ перейдёт в A, и мы получим
к нулю. При этом A’ перейдёт в A, и мы получим 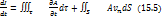
Как обычно, преобразуем интеграл по поверхности к интегралу по объёму: 
Таким образом, для производной 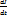 получим выражение
получим выражение
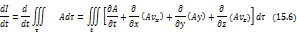
Подынтегральное выражение можно преобразовать к другому виду, раскрывая производные от произведений:
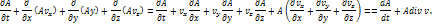
Div –дивергенция (дивергенция — это линейный дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность достаточно малой (в условиях конкретной задачи) окрестности каждой внутренней точки области определения поля.)
Соответственно равенство (15.6) примет вид 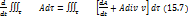
2.Вычисление 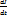 в переменных Лагранжа.
в переменных Лагранжа.
Рассмотрим объём 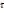 выделенной массы жидкости в момент времени t. Координаты частиц этого объёма можно записать в виде: x=x(a,b,c,t); y=y(a,b,c,t); z=z(a,b,c,t)
выделенной массы жидкости в момент времени t. Координаты частиц этого объёма можно записать в виде: x=x(a,b,c,t); y=y(a,b,c,t); z=z(a,b,c,t)
Где a,b,c – координаты этих частиц в момент времени  , когда декартовы координаты совпадали с координатами Лагранжа x=a, y=b, z=c, а объём
, когда декартовы координаты совпадали с координатами Лагранжа x=a, y=b, z=c, а объём 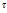 занимал объём
занимал объём 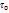 . В интеграле (15.1), который нужно дифференцировать, перейдём от переменных x,y,z к переменным Лагранжа. Тогда
. В интеграле (15.1), который нужно дифференцировать, перейдём от переменных x,y,z к переменным Лагранжа. Тогда 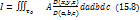
Но в этом случае объём интегрирования 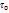 постоянен для всех моментов времени, и можно дифференцировать под знаком интеграла. Таким образом
постоянен для всех моментов времени, и можно дифференцировать под знаком интеграла. Таким образом

Сделаем переход в правой части равенства от переменных a, b, c к переменным x, y, z, учитывая при этом, что 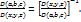
Тогда получим 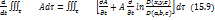
Билет 4. Закон сохранения массы (допущения, физическая формулировка, вывод уравнения закона в интегральной форме. Уравнение неразрывности (вывод, рассмотрение частных случаев).
Закон сохранения масс – это физический закон, справедливый для движений, происходящих со скоростями, незначительными по сравнению со скоростью света.
Предположим что в процессе движения жидкости нет ни возникновения ни, ни исчезновение массы. 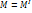 . По определению плотности
. По определению плотности 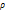 масса в объеме
масса в объеме 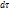 равна
равна 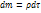 . Масса в объемах
. Масса в объемах 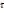 и
и 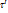 ровна:
ровна:
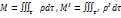 тогда
тогда 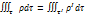 или
или 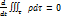 . Теперь пусть в объем
. Теперь пусть в объем 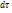 в течении времени
в течении времени 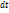 поступает масса жидкости
поступает масса жидкости 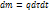 , q – плотность источников. Масса жидкости, которая в момент времени находилась в объеме будет изменяться во время движения. За время dt она получит приращение
, q – плотность источников. Масса жидкости, которая в момент времени находилась в объеме будет изменяться во время движения. За время dt она получит приращение 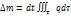 . За промежуток времени от t до tIприращение массы будет равно
. За промежуток времени от t до tIприращение массы будет равно 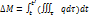 .
.
Теперь можем записать 𝑀I=𝑀+∆𝑀.Подставляем:
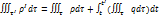 .
.
Это равенство – запись закона сохранения масс при наличии пространственно-распределенных источниковдля конечного объема и конечного промежутка времени. Теперь запишем для для бесконечно малого промежутка времени. 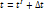 .
.
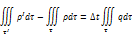 Поделив на
Поделив на 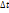 и устремив
и устремив 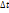 к нулю, получим
к нулю, получим 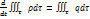 .
.
Это равенство – запись закона сохранения масс для конечного объема для данного момента времени при наличии пространственно-распределенных источников.
Уравнение неразрывности.
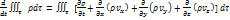 .
.
Подставив в уравнение выше мы получим: 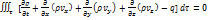
Это равенство имеет место для любого объема тао. Это возможно только когда подынтегральная функция равна нулю. Следовательно:
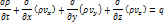 Раскрывая в этой формуле производные от произведений и вводя обозначение индивидуальной производной
Раскрывая в этой формуле производные от произведений и вводя обозначение индивидуальной производной 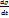 получим:
получим: 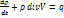
Получившаяся формула и есть запись закона сохранения масс в дифференциальной форме.
Пусть жидкость не сжимаема. Это означает, что плотность в движущейся частице не изменяется, то есть индивидуальная производная от плотности по времени равна нулю. 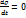
Уравнение неразрывности в этом случае имеет вид 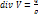 .
.
Рассмотрим уравнение, когда q=0.
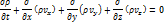 Вводя вектор
Вводя вектор 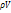 с проекциями
с проекциями  , можно уравнение переписать:
, можно уравнение переписать:

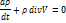 Частные случаи:
Частные случаи:
1 Движение установившееся. В этом случае местная производная 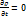 равна нулю:
равна нулю:
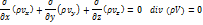 2 Жидкость не сжимаема. В этом случае
2 Жидкость не сжимаема. В этом случае 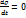 . Следовательно:
. Следовательно: 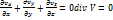
3 Движение плоское. Движение называется плоским, если существует такая плоскость, что все частицы жидкости движутся параллельно этой плоскости, причем на любой прямой, перпендикулярной этой плоскости, гидродинамические величины имею одно и то же значение. Принимая эту плоскость за плоскость (x,y) получим что 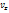 =0. Следовательно:
=0. Следовательно:
 .
.
Если движение установившееся то: 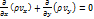
Если несжимаемая жидкость то: 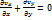
4 Одномерное движение с плоской симметрией.
Частица движется по прямой х. 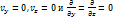
Уравнение неразрывности в этом 
Билет 5. Объемные и поверхностные силы в сплошной среде (определение плотности объемных и массовых сил и ее вычисление в случае действия сил тяжести, определение напряжений, вычисление главных векторов объемных и поверхностных сил). Закон изменения количества движения для движущегося жидкого объема (физическая формулировка, интегральная форма записи).
Объемные (далее массовые) силы – силы, действующие на каждый элемент объема независимо от того, имеются ли рядом другие части жидкости. Пусть FM – главный вектор сил, действующих на массу М жидкости, заполняющей объем τ. Средней массовой силой, действующей на массу М, называют величину 
Вектор 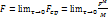 называется массовой силой, действующей в этой точке.
называется массовой силой, действующей в этой точке.
На объем 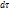 с массой
с массой 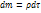 действует сила
действует сила 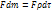 . Отсюда главный вектор массовых сил будет:
. Отсюда главный вектор массовых сил будет: 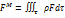
Поверхностные силы. Пусть объем τ ограничен поверхностью S. Жидкость, находящаяся вне объема, действует через поверхность S на жидкость внутри объема. Силы, с которыми частицы жидкости, находящиеся снаружи поверхности S, действуют на поверхностные частицы объема, называют поверхностными.
Выделим на S элемент поверхности 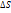 с нормалью n. Главный вектор поверхностных сил, действующий на
с нормалью n. Главный вектор поверхностных сил, действующий на 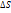 , обозначим
, обозначим  . Среднее напряжение, действующее на площадку
. Среднее напряжение, действующее на площадку 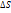 , будет
, будет 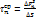 . Пусть площадка
. Пусть площадка 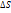 стягивается в точку.
стягивается в точку.
Вектор: 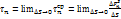 называют напряжением поверхностных сил, действующим в рассматриваемой точке.
называют напряжением поверхностных сил, действующим в рассматриваемой точке.
Главный вектор поверхностных сил, действующих на поверхность S: 
Поверхностные силы описывают взаимодействие между различными областями жидкости.
Интегральная запись закона количества движения.
Выделим в движущейся жидкости некоторый объем τ, ограниченный поверхностью S. Пусть вектор К – количество движения массы жидкости, заполняющей этот объем. В элементарном объеме 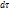 заключена масса
заключена масса 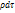 . Количество движения этой масс, имеющей скорость v:
. Количество движения этой масс, имеющей скорость v: 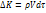 .
.
Количество движения массы, заключенной в объеме τ: 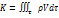
Для выделенной массы жидкости вектор К, как и объем – это функции времени.
Закон количества движения можно сформулировать так: производная по времени от количества движения некоторой системы масс равна главному вектору внешних сил, действующих на эту систему, следовательно: 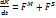
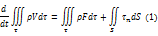 Проинтегрировав от t1 до t2 , получим запись закона для конечного промежутка времени:
Проинтегрировав от t1 до t2 , получим запись закона для конечного промежутка времени:  . (2)
. (2)
Изменение количества движения за некоторый промежуток времени равно сумме импульса массовых сил и импульса поверхностных сил.

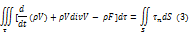 Равенства 1,2 и 3 дают интегральную запись закона количества движения.
Равенства 1,2 и 3 дают интегральную запись закона количества движения.
Билет 6 Формула Коши (вывод). Тензор напряжений



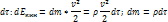
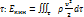 (4.1)
(4.1)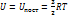 , Т – энергия единицы массы. R – газовая постоянная сорта газа.
, Т – энергия единицы массы. R – газовая постоянная сорта газа.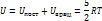
 (4.2)
(4.2)
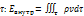 (4.3)
(4.3)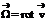 и его компоненты в декартовых координатах. Связь
и его компоненты в декартовых координатах. Связь 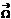 с угловой скоростью вращения жидкой частицы.
с угловой скоростью вращения жидкой частицы.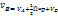
 - скорость полюса,
- скорость полюса,  - чисто деформационная скорость,
- чисто деформационная скорость, 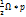 -скорость точки во вращательном движении затвердевшей жидкой частицы с угловой скоростью
-скорость точки во вращательном движении затвердевшей жидкой частицы с угловой скоростью 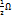 .
.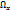 =
= 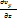 -
- 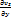 = 2
= 2 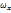 ,
,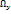 =
= 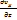 -
- 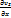 = 2
= 2 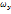 ,
,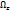 =
= 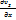 -
- 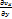 = 2
= 2 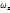 .
.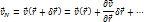
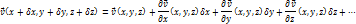
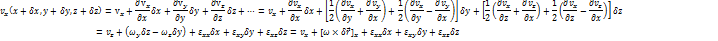
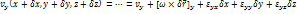
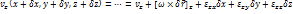
 (5.6)
(5.6)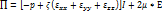 (6.1)
(6.1) (6.2)
(6.2)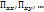 от компонент тензора скоростей деформации
от компонент тензора скоростей деформации 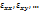 является линейной(свойство можно проследить из формулы 6.2)
является линейной(свойство можно проследить из формулы 6.2) 3)Если жидкость неподвижна или движется как абсолютно твердое тело, то в ней действуют только нормальные напряжения.
3)Если жидкость неподвижна или движется как абсолютно твердое тело, то в ней действуют только нормальные напряжения.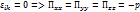 , остальные
, остальные 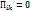 Нормальные напряжения в этом случае не зависят от ориентировки площадки.
Нормальные напряжения в этом случае не зависят от ориентировки площадки.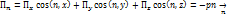
 (2.8)
(2.8) 

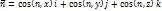
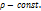 (1.8)
(1.8)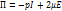 (6.3) Формула Стокса(1845 г.)
(6.3) Формула Стокса(1845 г.) (6.8)
(6.8)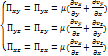 (6.9)
(6.9)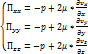 (6.10)
(6.10)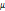 для несжимаемой жидкости часто рассматривают величину ν, называемую кинематическим коэффициентом вязкости
для несжимаемой жидкости часто рассматривают величину ν, называемую кинематическим коэффициентом вязкости 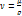 . Коэффициент
. Коэффициент 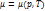 , но зависимость от давления слабая.
, но зависимость от давления слабая.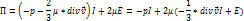
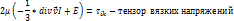
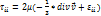 (6.11)
(6.11)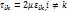
 (6.4)
(6.4)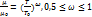 (6.5)
(6.5)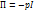 (6.12)
(6.12)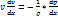
 получается известное уравнение Бернулли для несжимаемой жидкости:
получается известное уравнение Бернулли для несжимаемой жидкости: 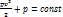
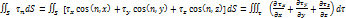
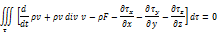
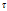 , то, следовательно
, то, следовательно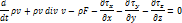
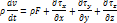
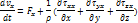
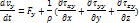
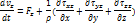
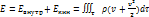 (4.4)
(4.4)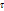 , со стороны жидкости вне
, со стороны жидкости вне 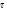 за счет механизма объемного поглощения тепла.
за счет механизма объемного поглощения тепла.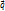 - направление в сторону теплового потока. Кол-во тепла, проходящее через единичную площадь. Тепло в жидкостях может передаваться за счет 2х существенно разных механизмов:
- направление в сторону теплового потока. Кол-во тепла, проходящее через единичную площадь. Тепло в жидкостях может передаваться за счет 2х существенно разных механизмов: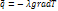 , коэф-т теплопроводности Дж/(м*с*К)(7.1)
, коэф-т теплопроводности Дж/(м*с*К)(7.1)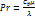 (7.2) число Прандтля
(7.2) число Прандтля (7.3)
(7.3)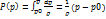 .
.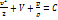 (2.12)
(2.12)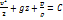 (2.13) или
(2.13) или 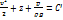 (2.14)
(2.14)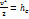 – скоростной, z – геометрической,
– скоростной, z – геометрической, 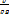 - пьезометрической высотами. Равенство (2.14) позволяет дать такую формулировку интеграла Бернулли: при движении однородной несжимаемой жидкости в поле сил тяжести сумма скоростной, пьезометрической и геометрической высот постоянна вдоль линии тока.
- пьезометрической высотами. Равенство (2.14) позволяет дать такую формулировку интеграла Бернулли: при движении однородной несжимаемой жидкости в поле сил тяжести сумма скоростной, пьезометрической и геометрической высот постоянна вдоль линии тока.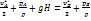
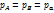 , получаем
, получаем 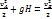
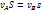
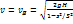
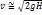
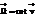 и его компоненты в декартовых координатах. Связь
и его компоненты в декартовых координатах. Связь  с угловой скоростью вращения жидкой частицы.
с угловой скоростью вращения жидкой частицы.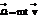 и его компоненты в декартовых координатах. Связь
и его компоненты в декартовых координатах. Связь 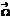 с угловой скоростью вращения жидкой частицы.
с угловой скоростью вращения жидкой частицы.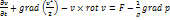
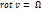 :
:
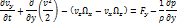
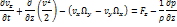
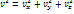
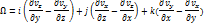
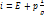 (3.1). Следовательно, при малых изменениях параметра состояния
(3.1). Следовательно, при малых изменениях параметра состояния 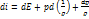
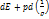 равна притоку тепла dq к системе. Если приток тепла к системе или отвод тепла от нее отсутствует, т.е. если процесс адиабатический, то dq=0 и
равна притоку тепла dq к системе. Если приток тепла к системе или отвод тепла от нее отсутствует, т.е. если процесс адиабатический, то dq=0 и 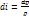 . Таким образом, адиабатического процесса равенство
. Таким образом, адиабатического процесса равенство 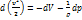 (при отсутствие массовых сил) можно записать в виде
(при отсутствие массовых сил) можно записать в виде 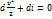 и соответственно интеграл Бернулли – в виде
и соответственно интеграл Бернулли – в виде 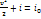 (3.2), где
(3.2), где  - значение энтальпии при v = 0.
- значение энтальпии при v = 0.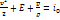
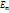 , вращательного
, вращательного 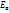 и колебательного
и колебательного 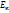 движения молекул(предполагается, что нет процессов диссоциации, ионизации и др.). В газовой динамике предполагают, что газ совершенный, а теплоемкость обычно считают постоянной, что справедливо в определенном диапазоне температуры, когда можно не учитывать колебательную энергию. В этом случае для двух атомных газов (воздух обычно рассматривают как смесь кислорода и азота)
движения молекул(предполагается, что нет процессов диссоциации, ионизации и др.). В газовой динамике предполагают, что газ совершенный, а теплоемкость обычно считают постоянной, что справедливо в определенном диапазоне температуры, когда можно не учитывать колебательную энергию. В этом случае для двух атомных газов (воздух обычно рассматривают как смесь кислорода и азота) 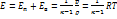 и энтальпия дается формулой
и энтальпия дается формулой 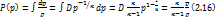 , а интеграл Бернулли имеет вид
, а интеграл Бернулли имеет вид 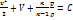 (2.17) при (V = 0). Если температуры таковы, что возбуждается и колебательная энергия
(2.17) при (V = 0). Если температуры таковы, что возбуждается и колебательная энергия 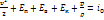
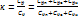 зависит от T.
зависит от T.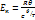 . Величина θ называется характеристическая температура
. Величина θ называется характеристическая температура  , где v – частота колебаний, h – постоянная Планка, а κ – постоянная Больцмана.
, где v – частота колебаний, h – постоянная Планка, а κ – постоянная Больцмана.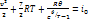
 (1.11) и интеграл Бернулли
(1.11) и интеграл Бернулли 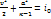 (2.19):
(2.19):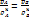 (4.1)
(4.1)
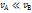 и можно принять
и можно принять  . Обозначая
. Обозначая 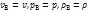 получаем из интеграла Бернулли (4.1)
получаем из интеграла Бернулли (4.1)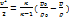 (4.2)
(4.2)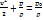
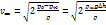
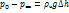
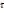 , ограниченный поверхностью S. Пусть в каждой точке (частице) этого объёма определена некоторая гидродинамическая величина A(скалярная, векторная или тензорная – безразлично). Рассмотрим интеграл.
, ограниченный поверхностью S. Пусть в каждой точке (частице) этого объёма определена некоторая гидродинамическая величина A(скалярная, векторная или тензорная – безразлично). Рассмотрим интеграл. 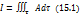
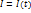 .
. 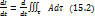
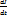 в переменных Эйлера и переменных Лагранжа.
в переменных Эйлера и переменных Лагранжа.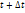 . Для момента времени t сохраним введённые обозначения: A(x,y,z,t)=A
. Для момента времени t сохраним введённые обозначения: A(x,y,z,t)=A 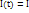 . Значение всех функций в момент t’=t+
. Значение всех функций в момент t’=t+ 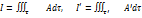
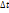 можем записать
можем записать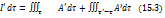 ->
-> 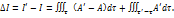
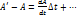
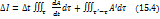
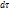 объёма
объёма 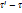 выберем в виде
выберем в виде 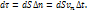 Тогда
Тогда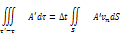
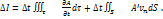
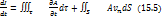

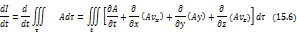
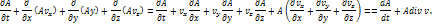
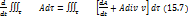
 , когда декартовы координаты совпадали с координатами Лагранжа x=a, y=b, z=c, а объём
, когда декартовы координаты совпадали с координатами Лагранжа x=a, y=b, z=c, а объём 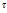 занимал объём
занимал объём 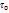 . В интеграле (15.1), который нужно дифференцировать, перейдём от переменных x,y,z к переменным Лагранжа. Тогда
. В интеграле (15.1), который нужно дифференцировать, перейдём от переменных x,y,z к переменным Лагранжа. Тогда 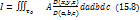

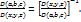
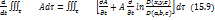
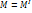 . По определению плотности
. По определению плотности 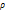 масса в объеме
масса в объеме 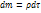 . Масса в объемах
. Масса в объемах 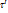 ровна:
ровна: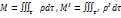 тогда
тогда 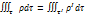 или
или 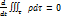 . Теперь пусть в объем
. Теперь пусть в объем 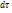 в течении времени
в течении времени 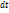 поступает масса жидкости
поступает масса жидкости 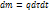 , q – плотность источников. Масса жидкости, которая в момент времени находилась в объеме будет изменяться во время движения. За время dt она получит приращение
, q – плотность источников. Масса жидкости, которая в момент времени находилась в объеме будет изменяться во время движения. За время dt она получит приращение 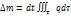 . За промежуток времени от t до tIприращение массы будет равно
. За промежуток времени от t до tIприращение массы будет равно 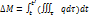 .
. 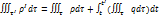 .
. 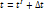 .
.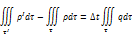 Поделив на
Поделив на 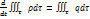 .
.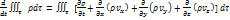 .
.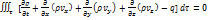
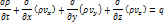 Раскрывая в этой формуле производные от произведений и вводя обозначение индивидуальной производной
Раскрывая в этой формуле производные от произведений и вводя обозначение индивидуальной производной 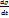 получим:
получим: 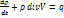
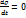
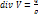 .
.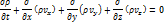 Вводя вектор
Вводя вектор 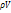 с проекциями
с проекциями  , можно уравнение переписать:
, можно уравнение переписать:
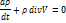 Частные случаи:
Частные случаи: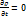 равна нулю:
равна нулю: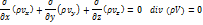 2 Жидкость не сжимаема. В этом случае
2 Жидкость не сжимаема. В этом случае 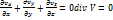
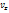 =0. Следовательно:
=0. Следовательно: .
.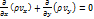
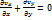
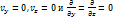


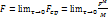 называется массовой силой, действующей в этой точке.
называется массовой силой, действующей в этой точке. 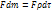 . Отсюда главный вектор массовых сил будет:
. Отсюда главный вектор массовых сил будет: 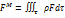
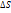 с нормалью n. Главный вектор поверхностных сил, действующий на
с нормалью n. Главный вектор поверхностных сил, действующий на  . Среднее напряжение, действующее на площадку
. Среднее напряжение, действующее на площадку 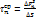 . Пусть площадка
. Пусть площадка 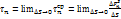 называют напряжением поверхностных сил, действующим в рассматриваемой точке.
называют напряжением поверхностных сил, действующим в рассматриваемой точке. 
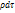 . Количество движения этой масс, имеющей скорость v:
. Количество движения этой масс, имеющей скорость v: 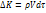 .
.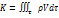
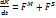
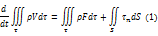 Проинтегрировав от t1 до t2 , получим запись закона для конечного промежутка времени:
Проинтегрировав от t1 до t2 , получим запись закона для конечного промежутка времени:  . (2)
. (2)
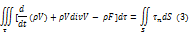 Равенства 1,2 и 3 дают интегральную запись закона количества движения.
Равенства 1,2 и 3 дают интегральную запись закона количества движения.


