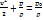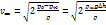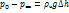Предположим, что жидкость идеальна, массовые силы консервативны, движение установившееся, имеет место баротропность на линии тока.
Так как жидкость идеальна, то уравнение движения  (2.1)
(2.1)
Так как массовые силы консервативны, то 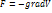 (2.2)
(2.2)
и уравнение (2.1) можно переписать в виде 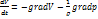 (2.3)
(2.3)
Предположение о баротропности на линии тока означает, что 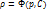 (2.4)
(2.4)
где С постоянная на линии тока.
При установившемся движении траектория и линия тока совпадают. Обозначим через dr(dx, dy, dz) элементарное перемещение вдоль линии тока и умножим скалярно все члены (2.3) на dr:  (2.5)
(2.5)
Так как линия тока является и траекторией, то
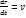 ,
, 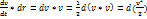 (2.6)
(2.6)
Кроме того, 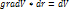 ,
, 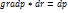 . (2.7)
. (2.7)
Подставим (2.6) и (2.7) в (2.5), получим 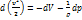 . (2.8)
. (2.8)
Имея ввиду (2.4), введем функцию P(p, C):  (2.9)
(2.9)
С учетом (2.9) равенство (2.8) можно переписать в виде 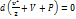 (2.10)
(2.10)
Отсюда  (2.11)
(2.11)
Равенство (2.10) и (2.11) имеют место на любой линии тока, но постоянная в правой части (2.11) может изменяться при переходе от одной линии тока в другую. Равенство (2.11) называют интегралом Бернулли.
Билет № 26 Уравнение Бернулли для несжимаемой жидкости в поле сил тяжести (получение уравнения, физическая интерпретация слагаемых). Истечение жидкости из сосуда через малое отверстие (задача Торичелли).
Уравнение Бернулли для несжимаемой жидкости. В этом случаи ρ-заданная постоянная и 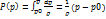 .
.
Интеграл Бернулли примет вид 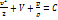 (2.12)
(2.12)
Если массовые силы – силы тяжести, то V=gz и интеграл Бернулли в этом случае
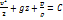 (2.13) или
(2.13) или 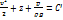 (2.14)
(2.14)
Отдельные слагаемые в (2.14) имеют размерность длины и называются соответственно: 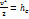 – скоростной, z – геометрической,
– скоростной, z – геометрической, 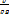 - пьезометрической высотами. Равенство (2.14) позволяет дать такую формулировку интеграла Бернулли: при движении однородной несжимаемой жидкости в поле сил тяжести сумма скоростной, пьезометрической и геометрической высот постоянна вдоль линии тока.
- пьезометрической высотами. Равенство (2.14) позволяет дать такую формулировку интеграла Бернулли: при движении однородной несжимаемой жидкости в поле сил тяжести сумма скоростной, пьезометрической и геометрической высот постоянна вдоль линии тока.
Истечение жидкости из сосуда через малое отверстие. Рассмотрим истечение жидкости из сосуда через отверстия. Будем считать, что отверстие расположено в близи дна. Жидкость предположим несжимаемой и находящийся в поле сил тяжести. Пусть S – площадь открытой поверхности жидкости в сосуде, s – площадь отверстия, H – уровень жидкости в сосуде.
Предполагаем, что s/S<< 1. Когда отверстие открыто, то уровень в сосуде понижается, хотя и медленно. Возникающее течение будет неустановившемся, но медленно изменяющемся во времени (s/S мало). Это движение можно приближенно рассматривать как последовательную смену установившихся движений. Такая трактовка неустановившихся движений носит название квазистационарной трактовки, или квазистационарного подхода. При таком подходе можем записать интеграл Бернулли, который для несжимаемой жидкости при V = gz для любой линии тока имеет вид (2.13).
Рассмотрим линию тока AB, проходящую через точку A поверхности S и точку B в сечение s. Записав интеграл Бернулли для точек A и B этой линии, будем иметь 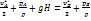
Принимая, что давление в точках A и B равно атмосферному 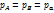 , получаем
, получаем 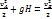
Уравнение неразрывности (постоянство расхода) приводит к соотношению
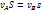
Из последних двух равенств найдем скорость истечения жидкости из сосуда 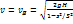
Так как s/S<< 1, то можно написать 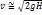
Последняя формула есть известная формула Торричелли. Скорость истечения не отличается от скорости материальной точки, падающей с высоты H.
Билет №12 Вектор 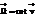 и его компоненты в декартовых координатах. Связь
и его компоненты в декартовых координатах. Связь  с угловой скоростью вращения жидкой частицы.
с угловой скоростью вращения жидкой частицы.
Вектор 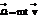 и его компоненты в декартовых координатах. Связь
и его компоненты в декартовых координатах. Связь 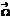 с угловой скоростью вращения жидкой частицы.
с угловой скоростью вращения жидкой частицы.
Уравнение Эйлера в форме Громеки – Лэмба: 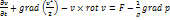
Запишем уравнение в проекции на оси, используя обозначение 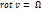 :
:

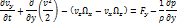
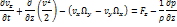
Здесь 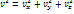
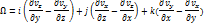
Уравнение Громеки – Лэмба содержат в явном виде вектор вихря Ω.
Компоненты скорости есть частные производные от φ(x,y,z,t) по координатам. Функцию φназывают потенциалом скоростей.
Билет №27 Уравнение Бернулли для совершенного газа (получение уравнения из общего интеграла Бернулли, переход к различным формам записи уравнения: через энтальпию, внутреннюю энергию, температуру). Уравнение Бернулли для несжимаемого газа (сравнение со случаем совершенного газа). Определение скорости потока несжимаемого газа с помощью трубки Пито–Прандтля.
Уравнение Бернулли для совершенного газа. В термодинамике энтальпия единицы массы газа определяется выражением 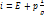 (3.1). Следовательно, при малых изменениях параметра состояния
(3.1). Следовательно, при малых изменениях параметра состояния 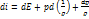
На основание первого начала термодинамике сумма 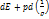 равна притоку тепла dq к системе. Если приток тепла к системе или отвод тепла от нее отсутствует, т.е. если процесс адиабатический, то dq=0 и
равна притоку тепла dq к системе. Если приток тепла к системе или отвод тепла от нее отсутствует, т.е. если процесс адиабатический, то dq=0 и 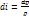 . Таким образом, адиабатического процесса равенство
. Таким образом, адиабатического процесса равенство 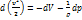 (при отсутствие массовых сил) можно записать в виде
(при отсутствие массовых сил) можно записать в виде 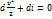 и соответственно интеграл Бернулли – в виде
и соответственно интеграл Бернулли – в виде 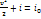 (3.2), где
(3.2), где  - значение энтальпии при v = 0.
- значение энтальпии при v = 0.
Если ввести в (3.2) выражение (3.1) для i, то будем иметь 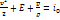
Здесь E – внутренняя энергия, складывающаяся в случае многоатомного газа из энергии поступательного 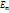 , вращательного
, вращательного 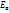 и колебательного
и колебательного 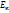 движения молекул(предполагается, что нет процессов диссоциации, ионизации и др.). В газовой динамике предполагают, что газ совершенный, а теплоемкость обычно считают постоянной, что справедливо в определенном диапазоне температуры, когда можно не учитывать колебательную энергию. В этом случае для двух атомных газов (воздух обычно рассматривают как смесь кислорода и азота)
движения молекул(предполагается, что нет процессов диссоциации, ионизации и др.). В газовой динамике предполагают, что газ совершенный, а теплоемкость обычно считают постоянной, что справедливо в определенном диапазоне температуры, когда можно не учитывать колебательную энергию. В этом случае для двух атомных газов (воздух обычно рассматривают как смесь кислорода и азота) 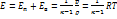 и энтальпия дается формулой
и энтальпия дается формулой 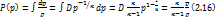 , а интеграл Бернулли имеет вид
, а интеграл Бернулли имеет вид 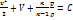 (2.17) при (V = 0). Если температуры таковы, что возбуждается и колебательная энергия
(2.17) при (V = 0). Если температуры таковы, что возбуждается и колебательная энергия 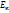 , то интеграл Бернулли надо писать в виде
, то интеграл Бернулли надо писать в виде 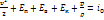
Для газа, находящегося в состоянии термодинамического равновесия, колебательная энергия есть функция температуры T, но при этом теплоемкость колебательных степеней свободы, а следовательно, и 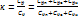 зависит от T.
зависит от T.
Выражение колебательной энергии для двухатомного газа 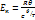 . Величина θ называется характеристическая температура
. Величина θ называется характеристическая температура  , где v – частота колебаний, h – постоянная Планка, а κ – постоянная Больцмана.
, где v – частота колебаний, h – постоянная Планка, а κ – постоянная Больцмана.
Интеграл Бернулли будет иметь вид 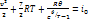
Уравнение Бернулли для несжимаемого газа. Пусть AB – линия тока, соединяющая точку A внутри сосуда с точкой B в сечение вытекающей струн. Для точек A и B можно записать адиабату Пуассона  (1.11) и интеграл Бернулли
(1.11) и интеграл Бернулли 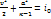 (2.19):
(2.19):
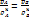 (4.1)
(4.1)

При большом сосуде и малом отверстии 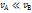 и можно принять
и можно принять  . Обозначая
. Обозначая 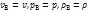 получаем из интеграла Бернулли (4.1)
получаем из интеграла Бернулли (4.1)
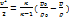 (4.2)
(4.2)
Определение скорости потока несжимаемого газа с помощью трубки Пито–Прандтля. 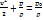
Отсюда 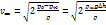
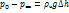



 (2.1)
(2.1)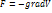 (2.2)
(2.2)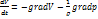 (2.3)
(2.3)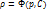 (2.4)
(2.4) (2.5)
(2.5)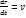 ,
, 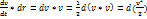 (2.6)
(2.6)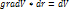 ,
, 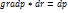 . (2.7)
. (2.7)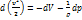 . (2.8)
. (2.8) (2.9)
(2.9)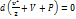 (2.10)
(2.10) (2.11)
(2.11)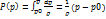 .
.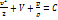 (2.12)
(2.12)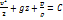 (2.13) или
(2.13) или 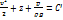 (2.14)
(2.14)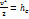 – скоростной, z – геометрической,
– скоростной, z – геометрической, 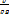 - пьезометрической высотами. Равенство (2.14) позволяет дать такую формулировку интеграла Бернулли: при движении однородной несжимаемой жидкости в поле сил тяжести сумма скоростной, пьезометрической и геометрической высот постоянна вдоль линии тока.
- пьезометрической высотами. Равенство (2.14) позволяет дать такую формулировку интеграла Бернулли: при движении однородной несжимаемой жидкости в поле сил тяжести сумма скоростной, пьезометрической и геометрической высот постоянна вдоль линии тока.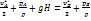
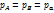 , получаем
, получаем 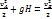
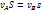
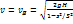
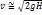
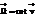 и его компоненты в декартовых координатах. Связь
и его компоненты в декартовых координатах. Связь  с угловой скоростью вращения жидкой частицы.
с угловой скоростью вращения жидкой частицы.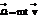 и его компоненты в декартовых координатах. Связь
и его компоненты в декартовых координатах. Связь 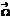 с угловой скоростью вращения жидкой частицы.
с угловой скоростью вращения жидкой частицы.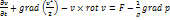
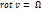 :
:
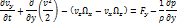
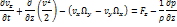
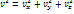
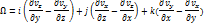
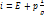 (3.1). Следовательно, при малых изменениях параметра состояния
(3.1). Следовательно, при малых изменениях параметра состояния 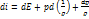
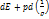 равна притоку тепла dq к системе. Если приток тепла к системе или отвод тепла от нее отсутствует, т.е. если процесс адиабатический, то dq=0 и
равна притоку тепла dq к системе. Если приток тепла к системе или отвод тепла от нее отсутствует, т.е. если процесс адиабатический, то dq=0 и 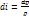 . Таким образом, адиабатического процесса равенство
. Таким образом, адиабатического процесса равенство 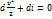 и соответственно интеграл Бернулли – в виде
и соответственно интеграл Бернулли – в виде 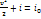 (3.2), где
(3.2), где  - значение энтальпии при v = 0.
- значение энтальпии при v = 0.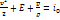
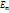 , вращательного
, вращательного 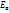 и колебательного
и колебательного 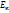 движения молекул(предполагается, что нет процессов диссоциации, ионизации и др.). В газовой динамике предполагают, что газ совершенный, а теплоемкость обычно считают постоянной, что справедливо в определенном диапазоне температуры, когда можно не учитывать колебательную энергию. В этом случае для двух атомных газов (воздух обычно рассматривают как смесь кислорода и азота)
движения молекул(предполагается, что нет процессов диссоциации, ионизации и др.). В газовой динамике предполагают, что газ совершенный, а теплоемкость обычно считают постоянной, что справедливо в определенном диапазоне температуры, когда можно не учитывать колебательную энергию. В этом случае для двух атомных газов (воздух обычно рассматривают как смесь кислорода и азота) 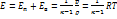 и энтальпия дается формулой
и энтальпия дается формулой 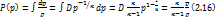 , а интеграл Бернулли имеет вид
, а интеграл Бернулли имеет вид 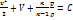 (2.17) при (V = 0). Если температуры таковы, что возбуждается и колебательная энергия
(2.17) при (V = 0). Если температуры таковы, что возбуждается и колебательная энергия 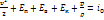
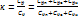 зависит от T.
зависит от T.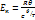 . Величина θ называется характеристическая температура
. Величина θ называется характеристическая температура  , где v – частота колебаний, h – постоянная Планка, а κ – постоянная Больцмана.
, где v – частота колебаний, h – постоянная Планка, а κ – постоянная Больцмана.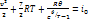
 (1.11) и интеграл Бернулли
(1.11) и интеграл Бернулли 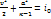 (2.19):
(2.19):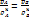 (4.1)
(4.1)
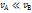 и можно принять
и можно принять  . Обозначая
. Обозначая 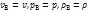 получаем из интеграла Бернулли (4.1)
получаем из интеграла Бернулли (4.1)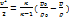 (4.2)
(4.2)