Если значение функции двух переменных z=z(x;y) известно в некоторой точке P0(x0,y0), то, применяя формулу (39), можно вычислить значения функции в достаточно близких P(x0+∆x,y0+∆y) точках.
Подставим координаты точки P вместо x и y в правую часть (39) и после преобразований получим
z(x0+∆x,y0+∆y) = z0(x0,y0) + 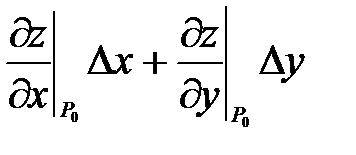 или
или
z(x0+∆x,y0+∆y) ≈ z0(x0,y0) + 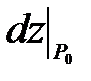 (40) Таким образом, к известному значению функции в точке необходимо прибавить значение дифференциала, вычисленного для этой точки.
(40) Таким образом, к известному значению функции в точке необходимо прибавить значение дифференциала, вычисленного для этой точки.
Пример. Вычислить значение 10.032 – 2.983. Рассмотрим функцию z = x2 – y3 и вычислим ее значение в точке P0(10;3). Получим z0(10;3) = 73. Теперь подсчитаем дифференциал функции, учитывая dx = 10.03 – 10 = 0.03, dy = 2.98 – 3 = - 0.02. Для этого найдем частные производные и вычислим их в точке P0(10;3) - 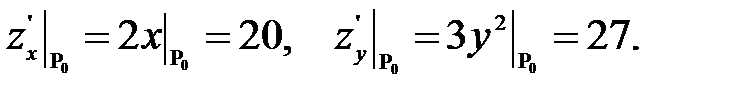 В результате подстановки всех вычисленных значений в формулу (40), получим z=z(10.03;2.98) = 73 + 20·0.03 - 27·0.02 = 73.06.
В результате подстановки всех вычисленных значений в формулу (40), получим z=z(10.03;2.98) = 73 + 20·0.03 - 27·0.02 = 73.06.
Лекция 10
§20 Производные сложных функций многих переменных
Пусть дана сложная функция z=z(x;y), аргументы которой в свою очередь являются функциями одной переменной – x = x(t), y = =y(t). Требуется вычислить производную функции z=z(x;y) по независимой переменной t.
Найдем дифференциал функции 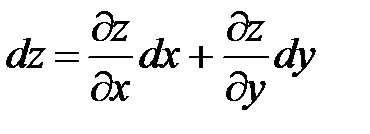 и разделим обе части его на dt. В результате получим формулу вычисления сложной функции:
и разделим обе части его на dt. В результате получим формулу вычисления сложной функции:
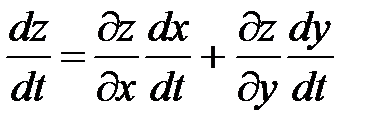 (41)
(41)
Пример. Вычислить производную функции z = sin(xy), если x = 2t, y = 3t3. Найдем частные производные функции z по x и y, и производные промежуточных аргументов x, y по t: 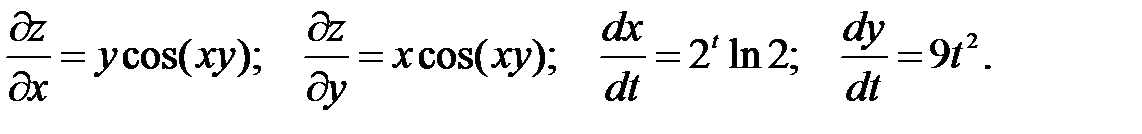 Подставим вычисленные производные в формулу (41) и получим производную функции по независимому аргументу -
Подставим вычисленные производные в формулу (41) и получим производную функции по независимому аргументу - 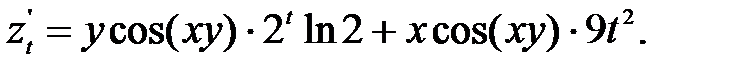
Пусть сложная функция z=z(x;y) является функцией многих независимых переменных, в частности 2-х – x = x(u,v), y = y(u,v). Требуется найти частные производные функции по независимым переменным 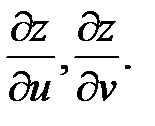 Согласно правилу вычисления частных производных, все переменные принимаются константами, кроме той, по которой находят производную. Следовательно, в этом случае функция z=z(x;y) становится функцией одной переменной и для отыскания производной может быть применена формула (41), но с обозначениями частных производных. Таким образом, получим
Согласно правилу вычисления частных производных, все переменные принимаются константами, кроме той, по которой находят производную. Следовательно, в этом случае функция z=z(x;y) становится функцией одной переменной и для отыскания производной может быть применена формула (41), но с обозначениями частных производных. Таким образом, получим
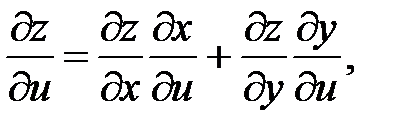 (42)
(42)
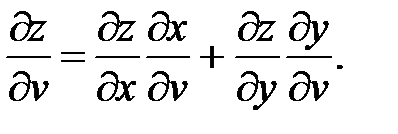 (43)
(43)
Анализируя формулы (41,42,43), можно сформулировать правило вычисления производных сложных функций многих переменных по независимой переменной –
Производная сложной функции по независимой переменной равна сумме произведений частных производных функции по промежуточным аргументам и производных соответствующих промежуточных аргументов по независимой переменной.
Пример. Вычислить производные функции s = x2y – (xyz)3/2 по переменной u и v, если x = u3 – v3, y = 2uv, z = vsinu.
Решение. Здесь x, y, z - промежуточные аргументы, u, v - независимые переменные (аргументы). Вычислим производные функции s по x, y, z –
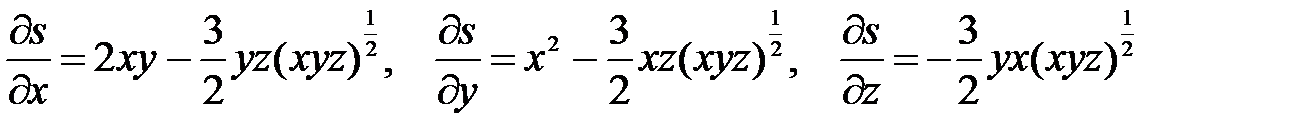 Теперь найдем производные промежуточных переменных по независимым u, v:
Теперь найдем производные промежуточных переменных по независимым u, v:
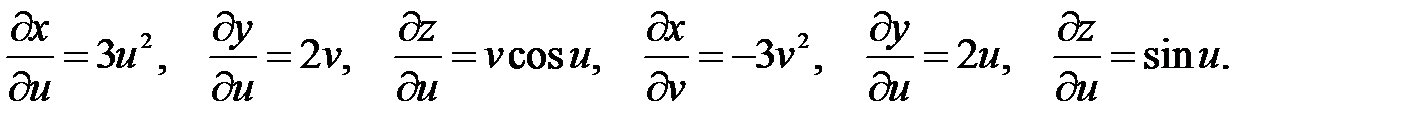 Применяя правило вычисления производных сложных функций, получим:
Применяя правило вычисления производных сложных функций, получим:
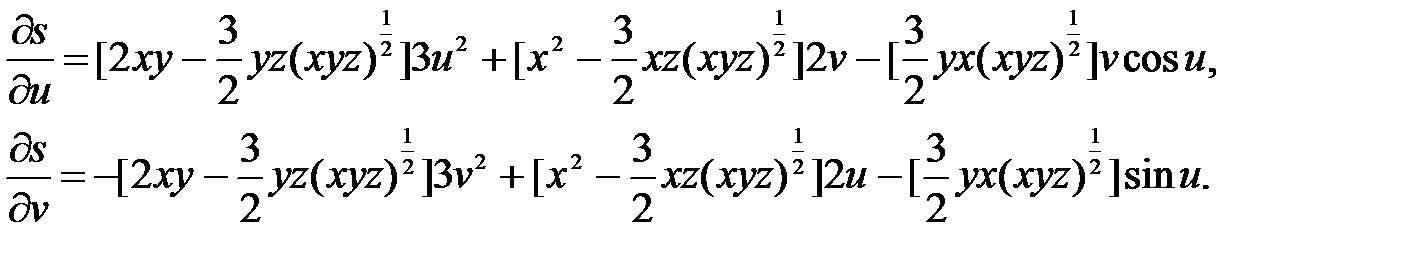
Пусть задана функция y = y(x) в неявном виде –
F(x, y(x)) = 0. (44)
Найдем производную по независимой переменной, продифференцировав равенство (44), учитывая, что левая часть есть сложная функция. Поэтому дифференцировать ее надо по выше сформулированному правилу: 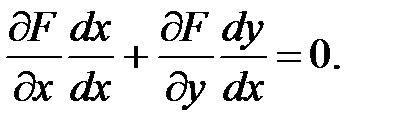 Разрешая равенство относительно y’, получим
Разрешая равенство относительно y’, получим 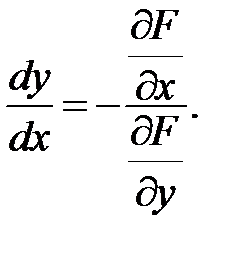 (45)
(45)
Если задана функция z=z(x;y) в неявной форме F(x, y, z(x,y)) = 0, то вычисляя производную функции многих переменных по переменной, получим 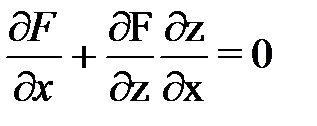 . Или
. Или
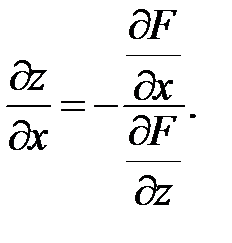 (46)
(46)
Аналогично рассуждая, получим производную по переменной y:
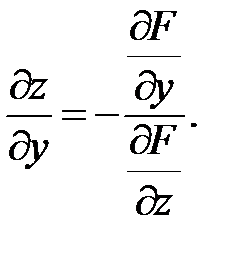 (47)
(47)
Пример. Найти производные функции z=z(x;y): z2y + x – arct(z-x) = 0. Найдем частные производные по переменным x, y, z функции F(x,y,z) = z2y + x – arct(z-x): 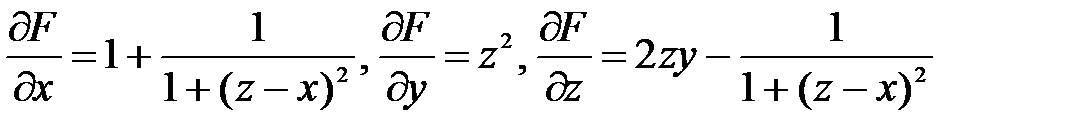 . Подставим в (46,47) и получим:
. Подставим в (46,47) и получим: 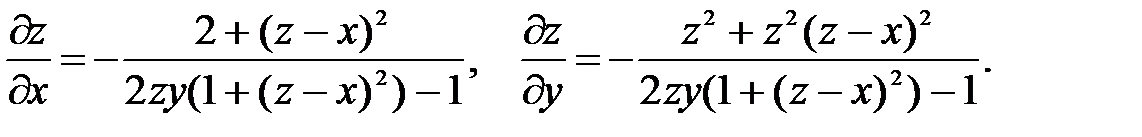
§21 Касательная плоскость и нормаль к поверхности.
Пусть поверхность задана уравнением F(x,y,z) = 0. Требуется написать уравнение касательной плоскости в заданной точке M0(x0,y0,z0).
Известно [§19 (39)], что уравнение касательной плоскости к поверхности z =z(x,y) имеет вид: 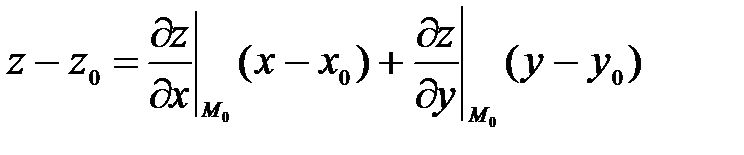 . А так как поверхность задана уравнением в неявном виде F(x,y,z) = 0, то, отыскивая частные производные по формулам (46) и (47) и подставляя их в уравнение плоскости, после необходимых преобразований получим:
. А так как поверхность задана уравнением в неявном виде F(x,y,z) = 0, то, отыскивая частные производные по формулам (46) и (47) и подставляя их в уравнение плоскости, после необходимых преобразований получим:  или
или
 (48)
(48)
Из аналитической геометрии известно, что уравнение плоскости через заданную точку есть скалярное произведение нормального вектора к плоскости 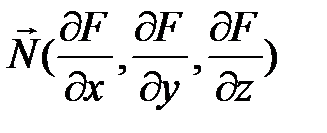 и текущего вектора M 0 M (x-x0,y-y0,z-z0). Так как нормаль к поверхности в заданной точке есть нормальный вектор к касательной плоскости в точке, то уравнение нормали принимает вид:
и текущего вектора M 0 M (x-x0,y-y0,z-z0). Так как нормаль к поверхности в заданной точке есть нормальный вектор к касательной плоскости в точке, то уравнение нормали принимает вид:
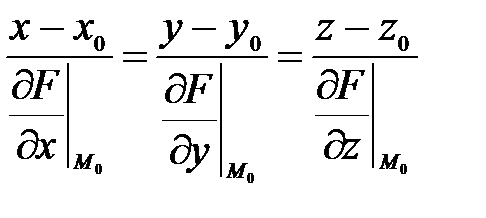 (49)
(49)
Пример. Написать уравнение касательной плоскости к поверхности x2 + y2 + z2=56,
параллельной плоскости 2x – y + 3z + 7 = 0.
Решение. Для написания уравнения касательной плоскости к поверхности следует найти координаты точки, принадлежащей поверхности. По условию координаты нормального вектора касательной плоскости должны быть пропорциональны координатам нормали заданной плоскости.
Найдем частные производные функции F(x,y,z) = x2 + y2 + z2-14 = 0 и удовлетворим условиям пропорциональности их соответствующим коэффициентам заданной плоскости: 2x = 2ρ, 2y = -ρ, 2z = 3ρ.
Разрешая равенства относительно переменных и подставляя их в уравнение поверхности, найдем коэффициент пропорциональности, при котором точка будет принадлежать поверхности: ρ2 + ρ2/4 + 9 ρ2/4 = 56; ρ2 = 4; ρ = ± 4.
Таким образом таких точек будет две:M1(4,-2,6) и M2(-4,2,-6).
Итак, уравнения касательных плоскостей, параллельных заданной, будут иметь вид: 2(x – 4) – (y +2) + 3(z – 6) = 0 и 2(x + 4) – (y -2) + 3(z + 6) = 0.
Уравнения нормалей к поверхности в этих точках будут:
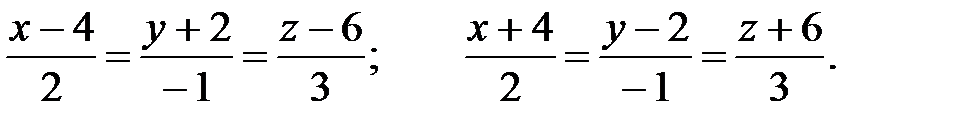
§22 Производные и дифференциалы высших порядков
функции двух переменных.
Очевидно, что частные производные функции z=z(x;y) также будут функциями двух переменных, так как фиксация переменных при вычислении частной производной произвольны. Поэтому от полученных частных производных можно в свою очередь найти частные производные.
Определение. Частные производные от частных производных функции z = z (x; y) называются частными производными второго порядка.
Частные производные второго порядка принято обозначать: 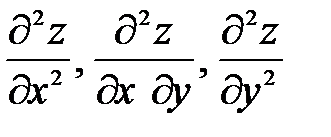 или
или
zxx, zxy, zyy. Следует заметить, что символы вторых производных неразделимы, т.е. символ  , как и другие, является целым и черта не означает деление или отношение. Нетрудно видеть, что от двух частных производных
, как и другие, является целым и черта не означает деление или отношение. Нетрудно видеть, что от двух частных производных 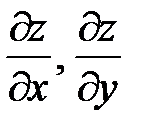 получаем четыре частные производные второго порядка
получаем четыре частные производные второго порядка 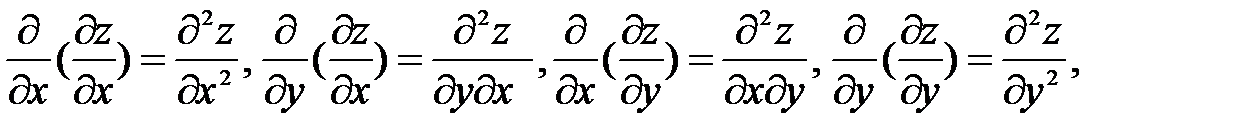 причем производные взятые по обеим переменным называются смешанными.
причем производные взятые по обеим переменным называются смешанными.
Теорема. Смешанные производные не зависят от порядка дифференцирования Покажем справедливость этой теоремы на примере дифференцирования функции z=cosxy.
zx = -ysin(xy), zyx = -sin(xy) – yxcos(xy),
zy = -xsin(xy), zxy = -sin(xy) - xycos(xy). Сравнивая вторые смешанные производные, видно что zyx = zxy.
Рассмотрим полный дифференциал функции z = z (x; y) (§18(38)) - 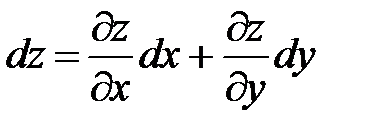 . Он зависит от частных производных, являющихся функциями независимых переменных (аргументов функции), и дифференциалов аргументов, которые не зависят от аргументов.
. Он зависит от частных производных, являющихся функциями независимых переменных (аргументов функции), и дифференциалов аргументов, которые не зависят от аргументов.
Определение. Вторым дифференциалом функции z = z (x; y) (дифференциалом второго порядка) называется дифференциал от первого дифференциала.
Вычисление второго дифференциала производится по тому же правилу что и первого. Найдем дифференциал второго порядка, который обозначается как d2z и читается де два зет:d2z = d(dz) = 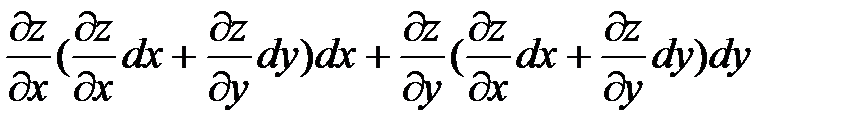 .Так как в правой части дифференциалы аргументов не зависят от переменных, то их можно выносить из под знака производной. Учитывая это и определение второй производной, получим:
.Так как в правой части дифференциалы аргументов не зависят от переменных, то их можно выносить из под знака производной. Учитывая это и определение второй производной, получим: 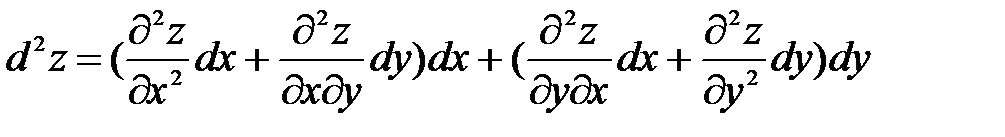 . Учитывая теорему о равенстве вторых смешанных производных, после соответствующих преобразований
. Учитывая теорему о равенстве вторых смешанных производных, после соответствующих преобразований
окончательно получим:
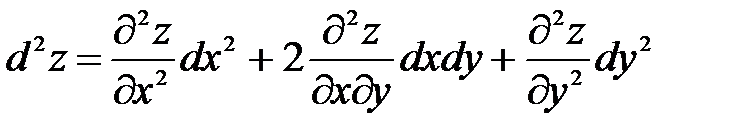 (50)
(50)
Дадим определения частных производных и дифференциалов N-го порядка.
Определение. Частной производной n –го порядка функции z = z (x; y) называется частная производная от частной производной n -1 порядка, т.е. 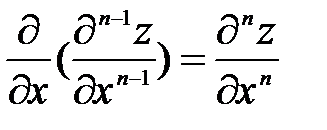 .
.
Теорема. Смешанная производная n -го порядка не зависит от порядка дифференцирования.
Определение. Дифференциал n –го порядка функции z = z (x; y) равен дифференциалу от дифференциала n –1=го порядка, т.е. dnz = d(dn-1z).
Лекция 11
§21. Экстремум функции двух переменных.
Заметим, что определение экстремума функции многих переменных формулируется аналогично определению экстремума функции одной переменной. Определение. Говорят, что функция z = z (x; y) принимает в точке P 0 (x 0; y 0) максимальное [минимальное] значение, если во всех точках достаточно малой ее ρ-окрестности выполняется условие z (x; y) < z (x 0; y 0) [ z (x; y) > z (x 0; y 0)].
Точки, в которых функция принимает максимальные и минимальные значения называются точками экстремума, а значения функции – экстремальными.
Пусть функция z = z(x;y) в точке P0(x0;y0) принимает экстремальное значение, например, максимум. Зафиксируем одну из координат функции y = y0 = const. При фиксированной координате функция z = z(x;y) становится функцией одной переменной z = z(x;y0). В курсе анализа функции одной переменной было показано, что необходимым условием экстремума является равенство нулю производной функции. Следовательно, для функции двух (многих) переменных необходимым условием будет равенство нулю частной производной.
Итак, для того чтобы дифференцируемая функция двух (многих) переменных имела экстремум в некоторой точке имела экстремум необходимо чтобы частные производные функции обращались в ноль.
Пример. Найти точки функции z = x2 +2xy + 4y0.5, производные в которых  равны нулю.
равны нулю. 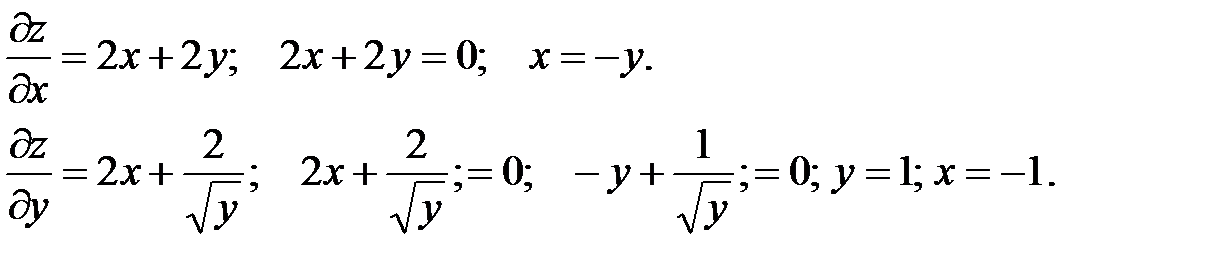
Если функция непрерывна в точке, но не дифференцируема, то в этой точке также может быть экстремум. Примером этого может служить функция 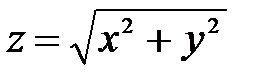 , изображением й функции является конус. Минимум этой функции в начале координат, но производных в этой точке не существует. Действительно. Рассмотрим производную функции по x:
, изображением й функции является конус. Минимум этой функции в начале координат, но производных в этой точке не существует. Действительно. Рассмотрим производную функции по x: 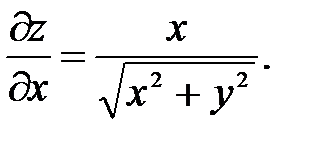 В начале координат производная не определена (0/0). Возьмем предел, устремляя «x» к нулю по прямой y = kx. В результате получим
В начале координат производная не определена (0/0). Возьмем предел, устремляя «x» к нулю по прямой y = kx. В результате получим 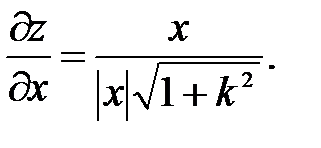 Не трудно видеть, что если x < 0, то
Не трудно видеть, что если x < 0, то 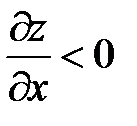 ,а если x > 0, то
,а если x > 0, то 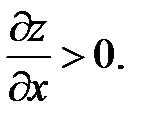 А это означает, что производная не существует.
А это означает, что производная не существует.
Итак, если функция не п рерывна в точке, но не дифференцируема, то эта точка подозрительна на экстремум.



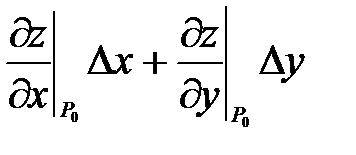 или
или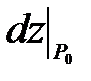 (40) Таким образом, к известному значению функции в точке необходимо прибавить значение дифференциала, вычисленного для этой точки.
(40) Таким образом, к известному значению функции в точке необходимо прибавить значение дифференциала, вычисленного для этой точки.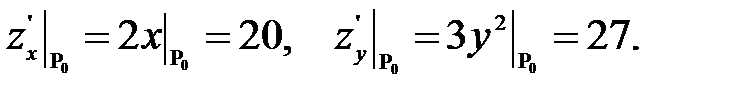 В результате подстановки всех вычисленных значений в формулу (40), получим z=z(10.03;2.98) = 73 + 20·0.03 - 27·0.02 = 73.06.
В результате подстановки всех вычисленных значений в формулу (40), получим z=z(10.03;2.98) = 73 + 20·0.03 - 27·0.02 = 73.06.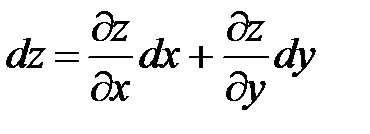 и разделим обе части его на dt. В результате получим формулу вычисления сложной функции:
и разделим обе части его на dt. В результате получим формулу вычисления сложной функции: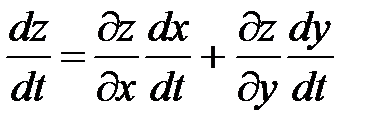 (41)
(41)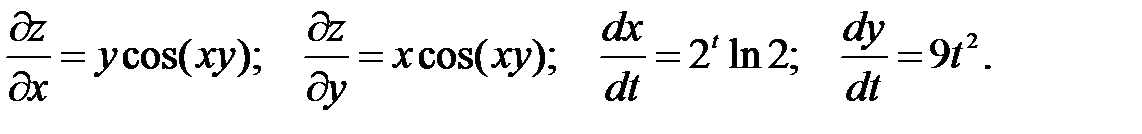 Подставим вычисленные производные в формулу (41) и получим производную функции по независимому аргументу -
Подставим вычисленные производные в формулу (41) и получим производную функции по независимому аргументу - 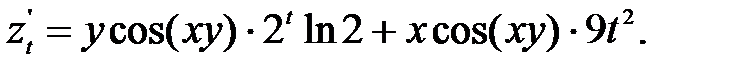
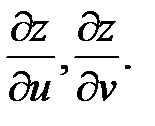 Согласно правилу вычисления частных производных, все переменные принимаются константами, кроме той, по которой находят производную. Следовательно, в этом случае функция z=z(x;y) становится функцией одной переменной и для отыскания производной может быть применена формула (41), но с обозначениями частных производных. Таким образом, получим
Согласно правилу вычисления частных производных, все переменные принимаются константами, кроме той, по которой находят производную. Следовательно, в этом случае функция z=z(x;y) становится функцией одной переменной и для отыскания производной может быть применена формула (41), но с обозначениями частных производных. Таким образом, получим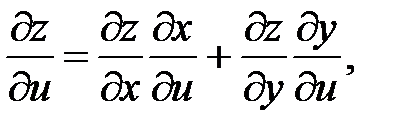 (42)
(42)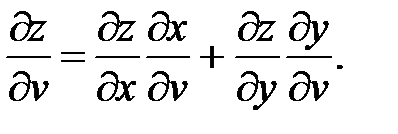 (43)
(43)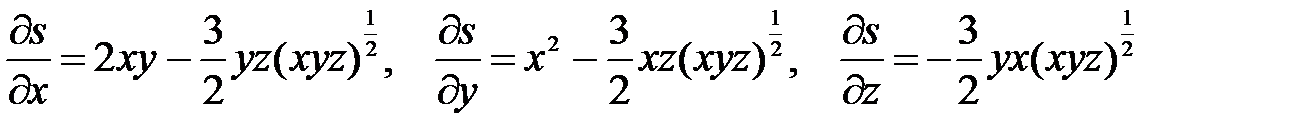 Теперь найдем производные промежуточных переменных по независимым u, v:
Теперь найдем производные промежуточных переменных по независимым u, v: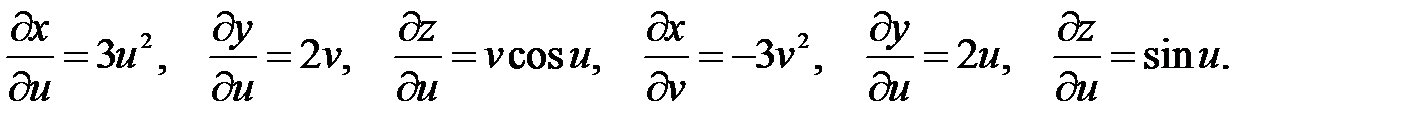 Применяя правило вычисления производных сложных функций, получим:
Применяя правило вычисления производных сложных функций, получим: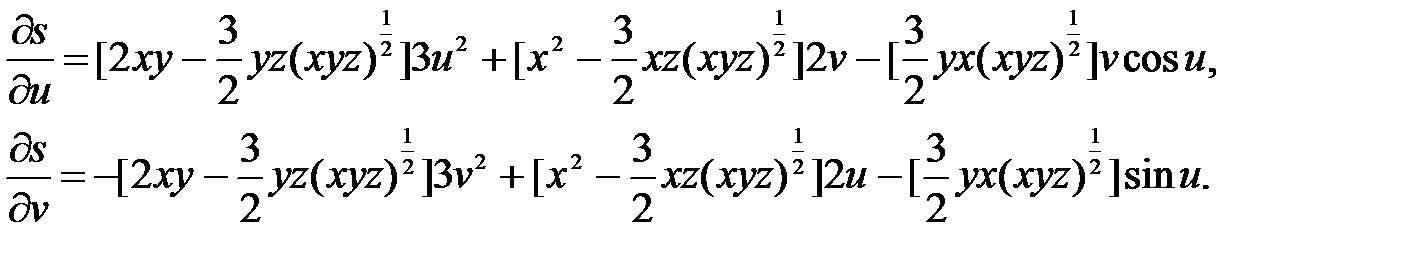
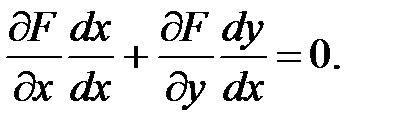 Разрешая равенство относительно y’, получим
Разрешая равенство относительно y’, получим 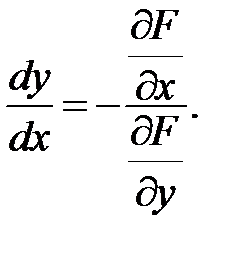 (45)
(45)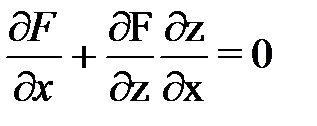 . Или
. Или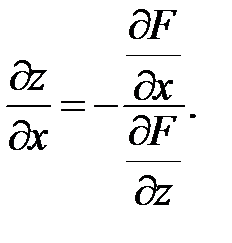 (46)
(46)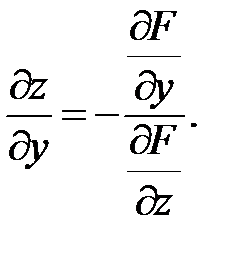 (47)
(47)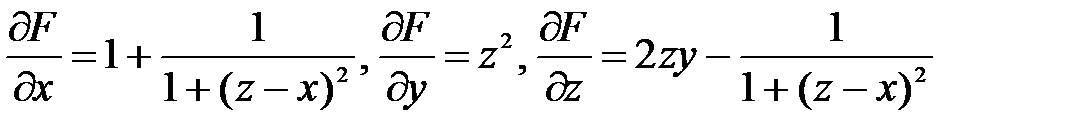 . Подставим в (46,47) и получим:
. Подставим в (46,47) и получим: 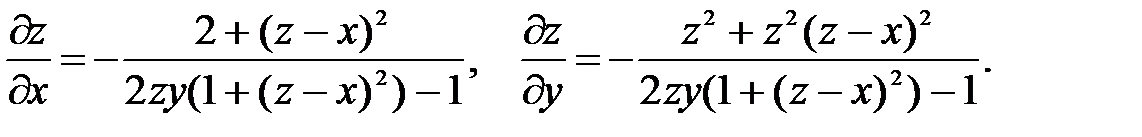
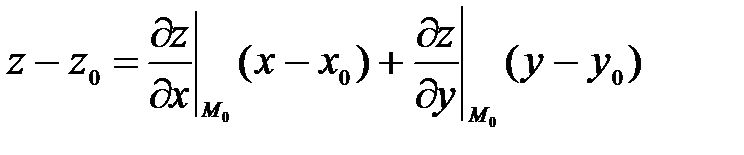 . А так как поверхность задана уравнением в неявном виде F(x,y,z) = 0, то, отыскивая частные производные по формулам (46) и (47) и подставляя их в уравнение плоскости, после необходимых преобразований получим:
. А так как поверхность задана уравнением в неявном виде F(x,y,z) = 0, то, отыскивая частные производные по формулам (46) и (47) и подставляя их в уравнение плоскости, после необходимых преобразований получим:  или
или (48)
(48)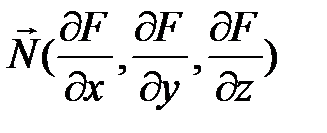 и текущего вектора M 0 M (x-x0,y-y0,z-z0). Так как нормаль к поверхности в заданной точке есть нормальный вектор к касательной плоскости в точке, то уравнение нормали принимает вид:
и текущего вектора M 0 M (x-x0,y-y0,z-z0). Так как нормаль к поверхности в заданной точке есть нормальный вектор к касательной плоскости в точке, то уравнение нормали принимает вид: 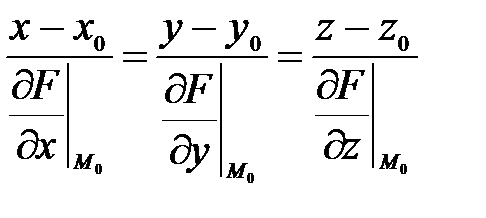 (49)
(49)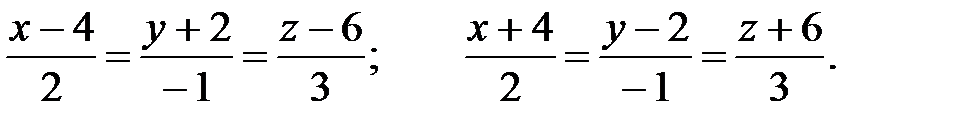
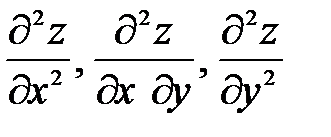 или
или , как и другие, является целым и черта не означает деление или отношение. Нетрудно видеть, что от двух частных производных
, как и другие, является целым и черта не означает деление или отношение. Нетрудно видеть, что от двух частных производных 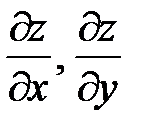 получаем четыре частные производные второго порядка
получаем четыре частные производные второго порядка 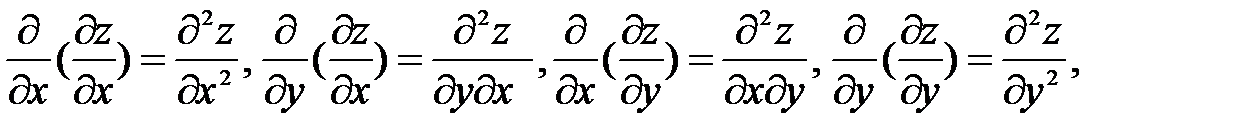 причем производные взятые по обеим переменным называются смешанными.
причем производные взятые по обеим переменным называются смешанными.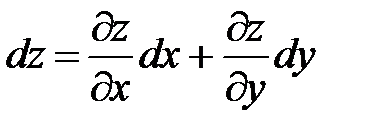 . Он зависит от частных производных, являющихся функциями независимых переменных (аргументов функции), и дифференциалов аргументов, которые не зависят от аргументов.
. Он зависит от частных производных, являющихся функциями независимых переменных (аргументов функции), и дифференциалов аргументов, которые не зависят от аргументов.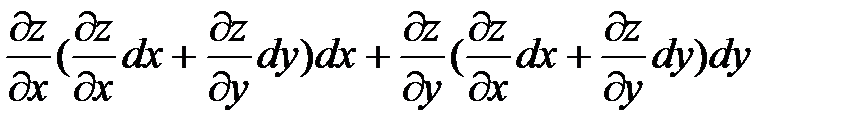 .Так как в правой части дифференциалы аргументов не зависят от переменных, то их можно выносить из под знака производной. Учитывая это и определение второй производной, получим:
.Так как в правой части дифференциалы аргументов не зависят от переменных, то их можно выносить из под знака производной. Учитывая это и определение второй производной, получим: 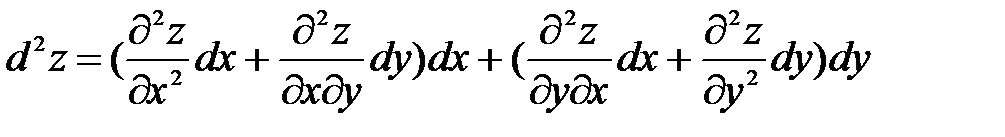 . Учитывая теорему о равенстве вторых смешанных производных, после соответствующих преобразований
. Учитывая теорему о равенстве вторых смешанных производных, после соответствующих преобразований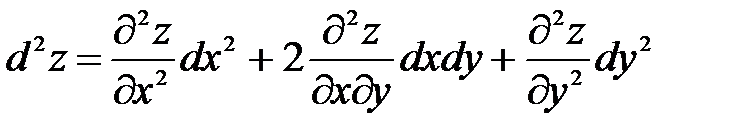 (50)
(50)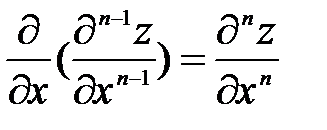 .
. равны нулю.
равны нулю. 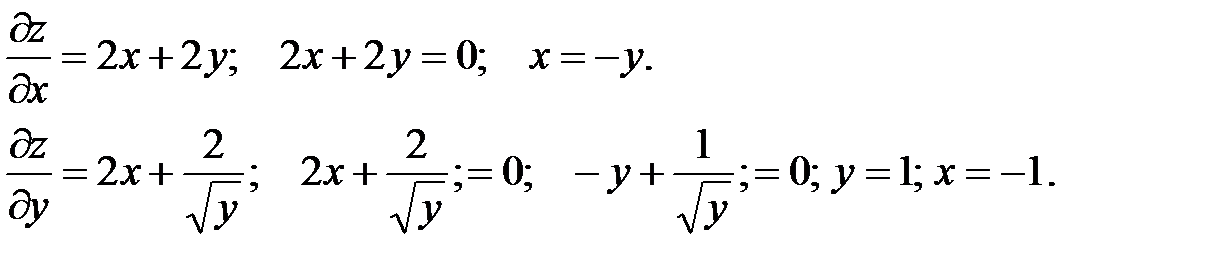
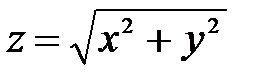 , изображением й функции является конус. Минимум этой функции в начале координат, но производных в этой точке не существует. Действительно. Рассмотрим производную функции по x:
, изображением й функции является конус. Минимум этой функции в начале координат, но производных в этой точке не существует. Действительно. Рассмотрим производную функции по x: 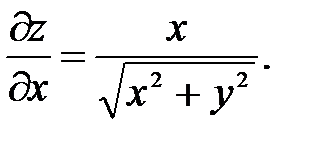 В начале координат производная не определена (0/0). Возьмем предел, устремляя «x» к нулю по прямой y = kx. В результате получим
В начале координат производная не определена (0/0). Возьмем предел, устремляя «x» к нулю по прямой y = kx. В результате получим 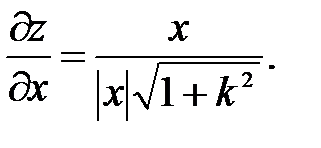 Не трудно видеть, что если x < 0, то
Не трудно видеть, что если x < 0, то 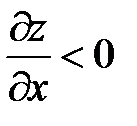 ,а если x > 0, то
,а если x > 0, то 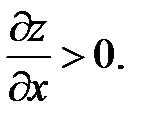 А это означает, что производная не существует.
А это означает, что производная не существует.


