Пусть задана функция г = г(φ) на множестве углов φ ϵ [α,β]. Разобьем угол φ лучами на n секторов, угол раствора каждого из которых ∆φi (i=1,2,3,…..,n). Внутри каждого элементарного сектора выберем угол θi и вычислим значение функции ri=r(θi). Теперь каждый элементарный криволинейный сектор заменим круговым радиуса ri=r(θi) и составим выражение вида r2(θi) ∆φi/2. Суммируя, вычисленные таким образом выражения, и увеличивая число элементарных секторов, приходим к пределу вида:
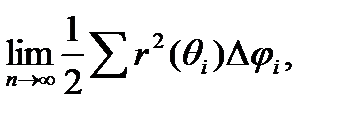
Который называется определенным интегралом в полярной системе координат. Этот предел принято обозначать
I =

который геометрически выражает площадь криволинейного сектора.
§13 Геометрические приложения определенного интеграла.
Выше было показано, что с помощью определенного интеграла можно вычислять площади плоских фигур, ограниченных кривыми, заданными уравнениями в декартовой и полярной системах координат. Если уравнения кривых заданы в параметрическом виде
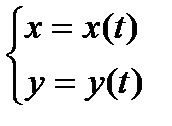 , то определенный интеграл принимает вид: I =
, то определенный интеграл принимает вид: I = 
Пример. Вычислить площадь фигуры, ограниченную кривой 
Решение. Так как аргумент и функция периодические с периодом 2π, то параметр меняется от 0 до 2π. Поэтому площадь фигуры
S = 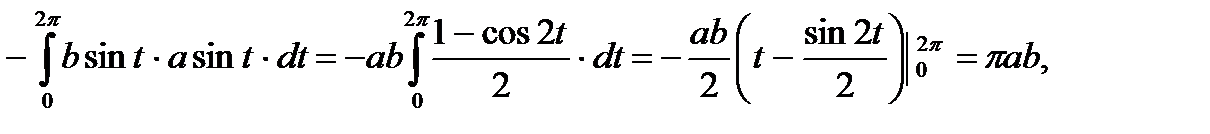
Пример. Вычислить площадь, ограниченную кривыми r = a(1+cos2φ); r = a, вне круга.
Решение. Найдем точки пресечения кривых, решая уравнения кривых совместно: a(1 + Cos2φ) = a, cos2φ = 0, 2φ = πk + π/2, φ = πk/2 + π/4. При k = 0 φ = π/4, k = -1 φ = -π/4.
Учитывая симметрию кривых относительно полярной оси, получим
S = 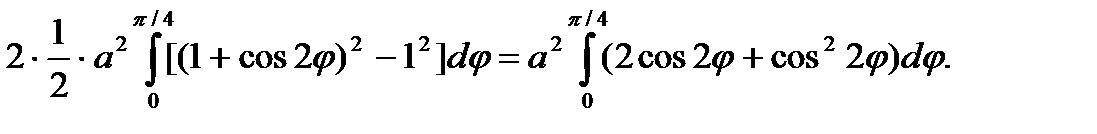
S = 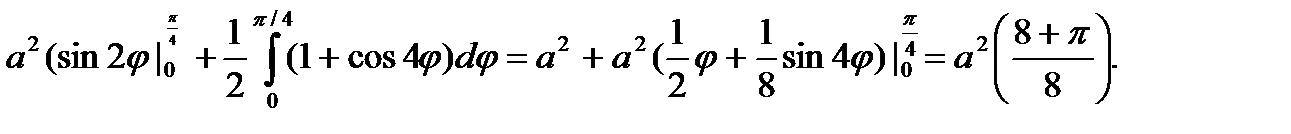
§14 Вычисление объёма тел вращения и длины плоской кривой.
Пусть непрерывная функция y = f(x) задана на отрезке [a;b]. Вращая криволинейную трапецию вокруг оси Ox, получим тело вращения, ограниченное с боков плоскостями x = a и x = b и поверхностью, полученную вращением графика функции. Объем такого тела вычисляется по формуле:
V = 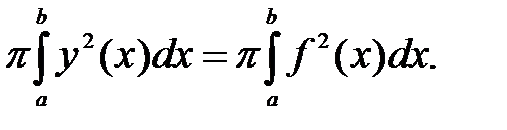 (27)
(27)
Если задана непрерывная функция x = φ(y) на отрезке [c;d] и получено тело вращения вокруг оси Oy способом, описанным выше, то объём тела вращения получим по формуле:
V =  (28)
(28)
Пусть непрерывная функция y = f(x) задана на отрезке [a;b] оси Ox и пусть график функции ограничен точками A и B. Длина кривой y = f(x) может быть вычислена по формуле:
 (29)
(29)
Формулы (27) и (29) предлагается вывести студентам самостоятельно, используя схему вывода определенного интеграла, учитывая следующие указания:
1. Отрезок [ a; b ] разбить на n элементарных участков ∆ xi;
2. Выводя формулу (27) через границы элементов разбиения провести плоскости перпендикулярные оси Ox и полученные диски заменить цилиндрическими.
3. Выводя формулу (29) через границы элементов разбиения провести прямые параллельные оси Oy до пересечения с кривой AB и полученные кривые на отрезках ∆ xi заменить хордами ∆ si.
Примеры.
1. Найти объём тела вращения кривой, заданной функцией y = x3 на отрезке [1;2], вокруг оси Oy.
Решение. Найдем ординаты концов отрезка оси Oy, на который проектируется кривая: y(1) = 1; y(2) = 23 = 8. Выразим x через y 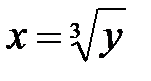 и применим формулу (28):
и применим формулу (28):
V = 
2. Найти объём тела вращения кривой, заданной функцией  вокруг оси Ox.
вокруг оси Ox.
Решение. функция является ограниченной по переменным. Найдем значения параметров, при которых кривая пересекает ось абсцисс: y = 0. Для этого решим уравнение Sint = 0 и получим t=0, t = π, которые будут являться пределами интегрирования, причем π будет нижним пределом. Так как функция задана в параметрическом виде, то в интеграле (27) подынтегральное выражение представим через параметр t, используя выражение функции и вычисляя дифференциал аргумента dx=bCostdt
В результате получим:
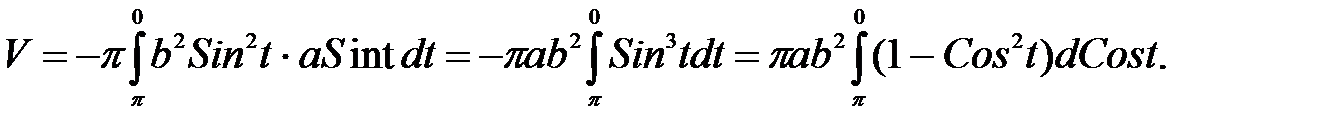
Таким образом, интегрируя, получим объём V =4πab2/3. Если a=b=r, то получим известную из школьного курса формулу V =4πr3/3– объем шара.
3. Найти длину кривой y = lnx на отрезке [1;4].
Решение. Для использования формулы (29) найдем производную функции =lnx: y’=1/x. Теперь

4. Вычислить длину кардиоиды, заданной уравнением r = a(1 - cos φ).
Решение. Длина кривой, заданной в полярной системе координат, вычисляется по формуле 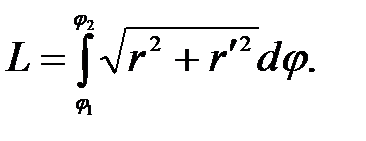 (30)
(30)
Заданная функция является четной и определена на множестве φ ϵ [o;2π]. Учитывая четность функции, интегрирование будем производить на множестве [0;π]. После вычисления производной функции и подстановке функции и ее производной, получим

§15 Несобственные интегралы.
Рассматривая определенный интеграл, мы полагали множество, на котором определена непрерывная функция, конечным, т.е. интеграл имеет конечные пределы.
Однако, нередко возникает необходимость распространить понятие определенного интеграла и на случаи, когда интервал интегрирования бесконечный (один или два предела бесконечны) или когда подынтегральная функция в пределах интервала интегрирования терпит разрыв.
Определение. Интегралы, пределы интегрирования которых не существуют или подынтегральная функция терпит разрыв на множестве точек интегрирования, называются несобственными.
Назовем несобственные интегралы с бесконечными пределами интегралами второго рода, а интегралы с разрывными функциями – первого рода.
Для того чтобы можно применить теорию интегрирования определенного интеграла к вычислению несобственных интегралов необходимо заменить бесконечный предел конечным и исключить точку разрыва, разбив интеграл на сумму двух интегралов.
Определение. Интеграл 2 рода 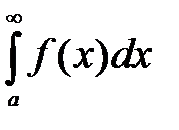 называется сходящимся, если существует предел
называется сходящимся, если существует предел 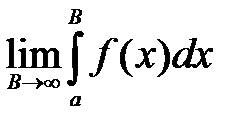 , причем значение предела считается значением предела. Если предел не существует, то интеграл – расходящийся.
, причем значение предела считается значением предела. Если предел не существует, то интеграл – расходящийся.
Заметим, что на несобственные сходящиеся  интегралы распространяются все свойства определенного интеграла.
интегралы распространяются все свойства определенного интеграла.
Пример. 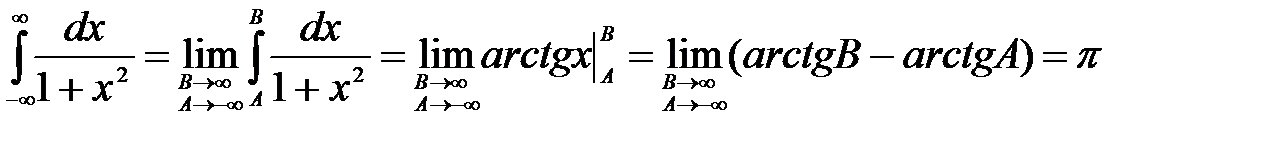
Несобственный интеграл сходится и его значение равно π. Геометрически это можно трактовать как значение площади фигуры, ограниченной графиком функции и осью Ox на бесконечном интервале.
Пусть теперь на отрезке [a;b] в точке x=c функция y=f(x) терпит разрыв.
Определение. Интеграл 1 рода 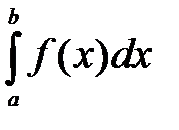 называется сходящимся, если существует предел
называется сходящимся, если существует предел 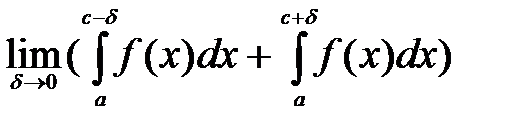 , причем значение предела считается значением предела. Если предел не существует, то интеграл – расходящийся.
, причем значение предела считается значением предела. Если предел не существует, то интеграл – расходящийся.
Пример. 
Несобственный интеграл сходится, так как предел существует.
Замечание. Во многих случаях требуется установить лишь сходимость несобственных интегралов, не отыскивая их значений. В этом случае используют признаки сравнения, которые здесь не приводятся.
Лекция 8



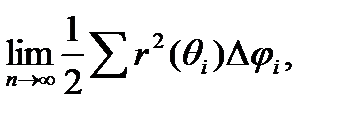

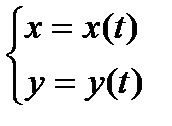 , то определенный интеграл принимает вид: I =
, то определенный интеграл принимает вид: I = 

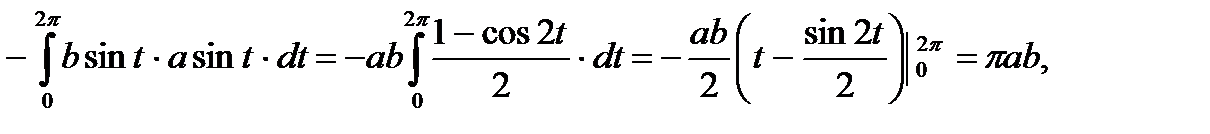
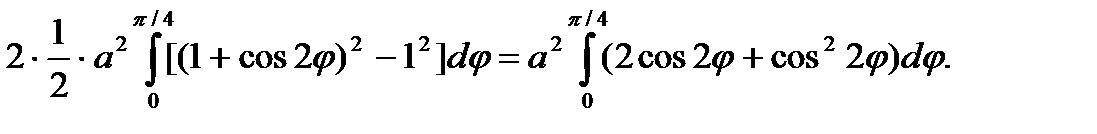
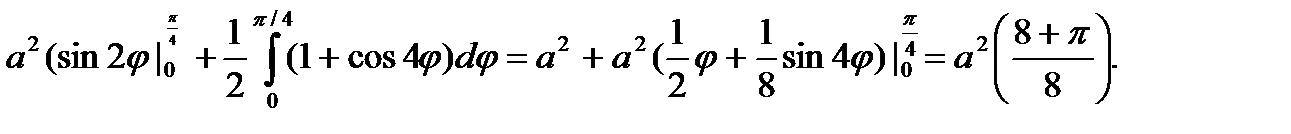
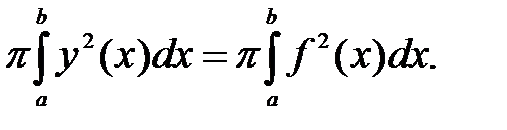 (27)
(27) (28)
(28) (29)
(29)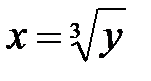 и применим формулу (28):
и применим формулу (28):
 вокруг оси Ox.
вокруг оси Ox.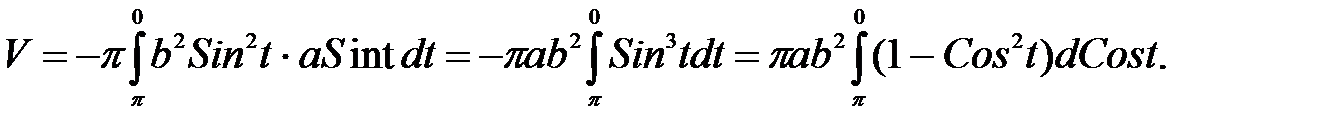

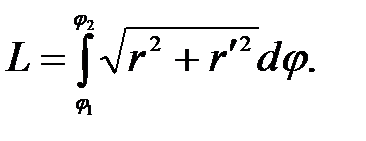 (30)
(30)
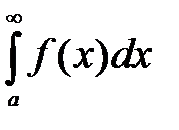 называется сходящимся, если существует предел
называется сходящимся, если существует предел 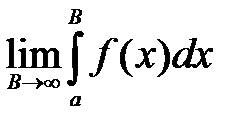 , причем значение предела считается значением предела. Если предел не существует, то интеграл – расходящийся.
, причем значение предела считается значением предела. Если предел не существует, то интеграл – расходящийся. интегралы распространяются все свойства определенного интеграла.
интегралы распространяются все свойства определенного интеграла.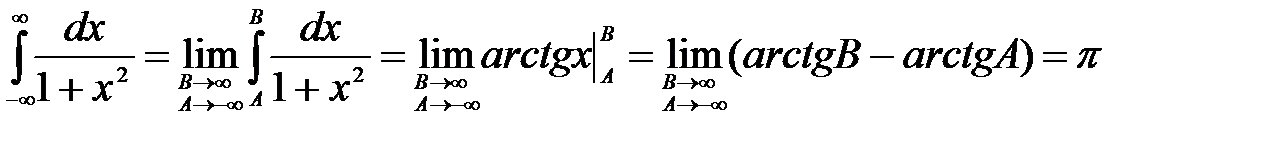
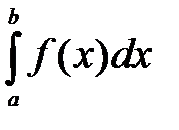 называется сходящимся, если существует предел
называется сходящимся, если существует предел 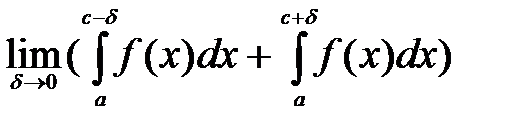 , причем значение предела считается значением предела. Если предел не существует, то интеграл – расходящийся.
, причем значение предела считается значением предела. Если предел не существует, то интеграл – расходящийся.



