Характер неустойчивости фазовых траекторий может быть различен. В некоторых случаях фазовые траектории не имеют предпочтительных областей в фазовом пространстве, а в других, напротив, фазовые траектории не выходят из некоторой подобласти фазового пространства системы. Если, несмотря на неустойчивость фазовых траекторий, все они (или их большинство) стремятся в некоторую подобласть фазового пространства, то можно говорить о некоторой специфической устойчивости, присущей движению системы. Выше устойчивые по Ляпунову траектории были определены как такие, для которых выполняется условие (5.8) при надлежащих начальных условиях. Если при этом

то решение (траектория) называется асимптотически устойчивым. Таким образом, притягивающее множество является множеством решений, асимптотически устойчивых. Притягивающие множества принято называть аттракторами[17]. Поскольку аттракторы – это некоторые области притяжения фазовых траекторий, более того, траектории здесь асимптотически устойчивы, то, казалось бы, на аттракторе не могут существовать расходящиеся траектории, стартующие из близкой окрестности. Это, однако, не так. Существуют аттракторы, на которых близкие фазовые траектории расходятся экспоненциально. Такие аттракторы называются странными. Здесь тем не менее, несмотря на экспоненциальную расходимость, траектории ограничены (именно это свойство позволяет выполнить условие асимптотической сходимости траекторий!).
Странные аттракторы являются свойствами диссипативных систем. Физически странный аттрактор реализуется, если в системе существует некоторое стационарное состояние, к которому притягиваются все (или почти все) ее фазовые траектории. Странный аттрактор хорошо наблюдаем при движении маятника, на который действуют вынуждающая сила и сила сопротивления. Стационарное состояние в такой системе достигается, если энергия, теряемая за один цикл из-за диссипации, будет в точности компенсирована за счет действия вынуждающей силы. В этом случае устанавливается периодический режим колебаний с постоянной амплитудой. Это состояние и является странным аттрактором, в чем легко убедиться, если теперь возмутить движение маятника, изменив его амплитуду и скорость. Спустя некоторое время установится прежний стационарный режим колебаний маятника.
Дадим теперь определение странного аттрактора. Пусть дана система 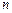 дифференциальных уравнений (5.2), которую можно записать в виде одного векторного уравнения
дифференциальных уравнений (5.2), которую можно записать в виде одного векторного уравнения

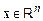 . (5.15)
. (5.15)
Решения этого уравнения образуют поток 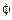 . Этот поток может иметь аттрактор
. Этот поток может иметь аттрактор 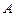 .
.
Определение. Аттрактором называется компактное множество в фазовом пространстве, обладающее свойствами: (i) 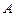 инвариантен относительно потока, т. е.
инвариантен относительно потока, т. е. 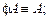 (ii)
(ii)  имеет нулевой объем в
имеет нулевой объем в 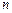 -мерном фазовом пространстве; (iii)
-мерном фазовом пространстве; (iii) 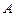 содержится в области
содержится в области 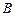 ненулевого объема, которая называется областью притяжения аттрактора.
ненулевого объема, которая называется областью притяжения аттрактора.
Областью притяжения аттрактора называется множество таких точек фазового пространства, что выходящие из них траектории при 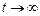 оказываются в
оказываются в 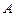 .
.
Наличие у системы аттрактора означает, что фазовые траектории с различными начальными данными оказываются с течением времени в некоторой общей области фазового пространства. Имеет место забывание начальных данных или нечувствительность к ним. Вместе с тем на странном аттракторе существует значительно более сильное свойство: первоначально близкие траектории на аттракторе экспоненциально разбегаются, порождая сколь угодно различные конечные состояния за конечное время. Таким образом, странный аттрактор экспоненциально усиливает первоначально имеющиеся неопределенности в задании начальных данных. И в этом смысле можно говорить об определенной обратной тенденции, система оказывается чрезвычайно чувствительной к заданию начальных условий.
Аттрактор Лоренца
Первый пример наблюдаемого странного аттрактора был построен Эдвардом Лоренцом из МТИ в 1961 году. Он моделировал конвекционные токи в атмосфере и свел исходную гидродинамическую задачу к решению трех обыкновенных дифференциальных уравнений
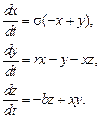 (5.16)
(5.16)
Это система с тремя степенями свободы, параметры 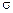 ,
, 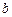 и
и 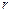 – некоторые постоянные. В экспериментах Э. Лоренца первые два параметра выбирались равными
– некоторые постоянные. В экспериментах Э. Лоренца первые два параметра выбирались равными 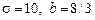 , а
, а 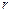 варьировался. Несмотря на внешнюю простоту, данная система уравнений аналитически неинтегрируема. Ее, однако, не сложно решить численно. Оказалось, что начиная с некоторых значений параметра
варьировался. Несмотря на внешнюю простоту, данная система уравнений аналитически неинтегрируема. Ее, однако, не сложно решить численно. Оказалось, что начиная с некоторых значений параметра 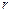 наблюдаемая временная эволюция функций
наблюдаемая временная эволюция функций 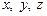 становится нерегулярной и очень чувствительна к изменению начальных условий. В экспериментах Э. Лоренца
становится нерегулярной и очень чувствительна к изменению начальных условий. В экспериментах Э. Лоренца 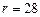 . Типичное поведение функции
. Типичное поведение функции 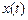 представлено на рис. 5.3. Здесь траекто-
представлено на рис. 5.3. Здесь траекто-
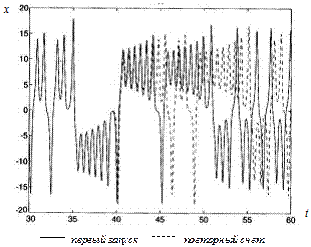
Рис. 5.3. Типичное поведение функции 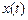 для системы
для системы
уравнений Лоренца
рии, отмеченные непрерывной и пунктирной кривыми, соответствуют двум разным, но мало отличающимся начальным данным. Как мы видим, имеет место существенная чувствительность к заданию начальных условий, что и характерно для странного аттрактора. Траектория движения в фазовом пространстве показана на рис. 5.4. Она выходит из начала координат и устремляется к области  , которая и образует странный аттрактор, состоящий из двух петель вокруг точек С и С ¢.
, которая и образует странный аттрактор, состоящий из двух петель вокруг точек С и С ¢.
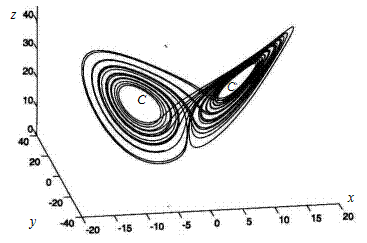
Рис. 5.4. Аттрактор Лоренца
Внешний эффект, произведенный системой Лоренца (5.16), был особенно неожидан, из-за того что сама система казалась чрезвычайно простой. Ученое сообщество было вполне подготовлено к тому, что нелинейная система с большим числом степеней свободы поведет себя непредсказуемо. Даже в высокопрофессиональных учебниках и монографиях по физике можно встретить утверждения, что молекулы рассматриваемого газа, например, движутся стохастически. Как рождаются такие утверждения, не очень понятно, поскольку почти тут же мы встречаемся с обычной точкой зрения о том, что их динамика описывается системой дифференциальных уравнений Ньютона (а значит, поведение системы молекул обязано быть детерминированным!). В душах исследователей почти всегда присутствовала интуитивная убежденность о стохастическом поведении системы с большим числом степеней свободы. Но, оказывается, и система малого числа степеней свободы может вести себя столь же непредсказуемо. Как же это все-таки сопрягается с детерминированностью решений соответствующих дифференциальных уравнений, и в каком смысле можно говорить о стохастическом поведении динамической системы?
Динамический хаос
На примере аттрактора Лоренца мы убедились, во-первых, в том, что динамические траектории системы могут иметь весьма сложное поведение, по крайней мере внешне мало чем отличающееся от поведения стохастической системы (см. рис. 5.4). Оказывается, что это не только кажущееся свойство. Сначала некоторые наводящие рассуждения. Положим, на экране дисплея мы имеем проекцию аттрактора Лоренца. Тогда мы увидим, как представляющая точка оказывается то на правой, то на левой ленте проекции аттрактора. Эти перескоки происходят внешне совершенно случайно, как если бы мы кидали монету и подсчитывали число «орлов» и «решек». Описанную процедуру можно формализовать. Если представляющая точка будет на правой ветви, будем писать нуль, на левой – единицу. Тогда для описания непрерывного динамического процесса мы получим дискретный способ описания, получивший название символьной динамики. Оказывается, что в терминах символьной динамики динамическую систему, имеющую странный аттрактор, нельзя отличить от серии испытаний, получаемой при бросании монеты, т. е. от стохастической системы. Таким образом, подобные динамические системы действительно имеют определенные свойства стохастических систем.
И второе важное обстоятельство. При исследовании реальных систем мы имеем дело с системами большого числа степеней свободы. Например, при изучении воздуха в комнате объемом
60 м3 при обычных условиях необходимо проследить за эволюцией примерно 1027 молекул. Ясно, что о реальных начальных данных для такой системы частиц мы ничего сказать не можем. Даже если бы мы имели прибор, позволяющий нам измерить это невообразимое число динамических переменных, сделать нам это удалось бы лишь с конечной точностью. Вместе с тем рассматриваемая система является системой с перемешиванием. Поэтому даже малая погрешность в измерениях вывела бы нас совсем не на ту фазовую траекторию, которая в данный момент реализуется в системе. Следовательно, в деле предсказания будущего по начальным значениям даже такие измерения нам не помогли бы. Измерения в принципе не могут решить такую задачу! В рассматриваемых динамических системах существуют принципиальные ограничения на возможность прогноза. В статистической физике за неимением лучшей гипотезы предполагается, что в состоянии равновесия все микроскопические состояния системы равновероятны. Это означает, что в любом из них система проводит одинаковое время. Это фактически означает, что при определении той или иной интересующей нас динамической величины мы проводим усреднение по всем начальным состояниям. Но так же мы поступаем и при описании стохастических процессов.
Таким образом, несмотря на то что реальные динамические системы имеют все атрибуты детерминированной системы, их поведение столь сложное, трудно предсказуемо и имеющее ряд черт, характерных лишь для стохастических систем, что можно говорить о динамическом хаосе. Здесь мы намеренно не делали различий между диссипативными и недиссипативными динамическими системами. Нам хотелось подчеркнуть, что хаотические свойства в динамических системах возникают из-за перемешивающегося характера движения динамических систем. Для диссипативных систем это перемешивание имеет место, однако лишь в некоторой области фазового пространства на аттракторе, тогда как в недиссипативной системе движение имеет перемешивающий характер во всем фазовом пространстве системы. Кроме того, диссипативные динамические системы описываются необратимыми во времени уравнениями, тогда как недиссипативные системы описываются обратимыми уравнениями[18]. Обратимыми, например, являются уравнения Ньютона (5.3), описывающие динамику системы  взаимодействующих частиц (см. следующий раздел). Существуют, конечно, и другие важные отличия, но о них мы поговорим позднее.
взаимодействующих частиц (см. следующий раздел). Существуют, конечно, и другие важные отличия, но о них мы поговорим позднее.
Динамические системы, в которых имеют место локальная неустойчивость и перемешивание, принято называть К-сис-темами в честь А.Н. Колмогорова, которому принадлежат фундаментальные идеи и результаты по исследованию динамических систем. Оказывается, что большинство динамических систем являются К-системами. Свойствами перемешивания обладают и недиссипативные динамические системы, в частности гамильтоновы системы, изучению которых будет посвящено несколько разделов ч. II. в шестидесятых годах ХХ в. Я.Г. Синай доказал ряд теорем, где установил, что К-сис-темами могут быть и системы малого числа степеней свободы. В частности, уже система двух (или более) упругих шаров является К-системой.
Будущее есть не то, что идет
к нам, а то, к чему мы идем.
М. Гюйо
Должен существовать принцип вроде: «Из елки можно сделать палку, а из палки не сделаешь елки».
Ричард Фейман
Необратимость есть проявление
в макроскопическом масштабе
стохастичности, существующей в микроскопическом масштабе.
Людвиг Больцман
Динамика и необратимость
Важнейшим свойством системы уравнений Ньютона (5.3), описывающей динамику  частиц, является их инвариантность относительно преобразования инверсии времени:
частиц, является их инвариантность относительно преобразования инверсии времени: 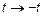 . При этом импульсы частиц также изменяют знак,
. При этом импульсы частиц также изменяют знак, 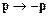 . Математически эта инвариантность связана с тем, что в уравнения Ньютона входят вторые производные от радиусов-векторов по времени. Уравнения механики, таким образом, инварианты относительно времени. Именно в этом смысле и уравнения механики описывают обратимые процессы. Отсюда, в частности, следует, что фазовые траектории прямого движения системы совпадают с фазовыми траекториями обращенного во времени движения. Но тогда со всей остротой встает вопрос, поставленный Дж. Николисом: «Как вообще возможна эволюция?» Действительно, эволюционное движение предполагает выделенность направления времени и неинвариантно относительно его обращения.
. Математически эта инвариантность связана с тем, что в уравнения Ньютона входят вторые производные от радиусов-векторов по времени. Уравнения механики, таким образом, инварианты относительно времени. Именно в этом смысле и уравнения механики описывают обратимые процессы. Отсюда, в частности, следует, что фазовые траектории прямого движения системы совпадают с фазовыми траекториями обращенного во времени движения. Но тогда со всей остротой встает вопрос, поставленный Дж. Николисом: «Как вообще возможна эволюция?» Действительно, эволюционное движение предполагает выделенность направления времени и неинвариантно относительно его обращения.
Все процессы, сопровождающие нас в жизни, и сама жизнь отмечены раз и навсегда заданным вектором времени. Они неинвариантны относительно обращения времени, и в этом смысле мы их называем необратимыми. Экспериментальным отражением наблюдаемой необратимости природных явлений явился второй закон термодинамики, который в общепринятой сегодня трактовке имеет статистический характер и утверждает, что наиболее вероятным является такое развитие процессов в замкнутых системах, когда их энтропия возрастает. Как примирить обратимость уравнений механики (и квантовой механики)[19] и наблюдаемые в природе необратимые явления? Какова природа этой необратимости?
Долгое время самый традиционный ответ на этот вопрос состоял в том, что наблюдаемая необратимость связана с той или иной неполнотой описания системы. В частности, при изучении систем большого числа частиц мы всегда вынуждены переходить от подробного динамического к некоторому огрубленному уровню описания. Именно в этом переходе необратимо теряется часть информации об эволюции системы. Таким образом, необратимость связана с потерей части информации о состоянии системы.
Эта точка зрения с годами трансформировалась. Существенное влияние на нее оказали исследования нескольких последних десятилетий в области теории динамических систем, краткое описание которых было дано выше. Известно, что обратимость и детерминизм решений системы уравнений Ньютона (5.3) возможны лишь при абсолютно точном задании начальных условий. Рассматриваемые нами системы большого числа частиц являются сильно неустойчивыми динамическими системами. Более того, по-видимому, во всех реальных системах движение в фазовом пространстве является движением с перемешиванием. При перемешивании две фазовые точки, которые в начальный момент были близки друг к другу, с течением времени быстро расходятся. Следовательно, сколь угодно малые возмущения начальных условий приводят к как угодно сильному уходу фазовой траектории от ее невозмущенного значения. Фазовые траектории в этом случае разбегаются экспоненциально.
Поэтому ясно, что если начальные условия для динамической системы заданы с какой-либо погрешностью, ее эволюция становится необратимой. Необратимость поведения системы связана в таком случае с неточностью задания начальных данных. Конечно, мы не можем измерить (а значит, и задать) бесконечно точно динамическое состояние системы. Это побудило очень многих исследователей считать, что наблюдаемая необратимость субъективна и имеет иллюзорный характер. Она связана лишь с ошибками измерений и несовершенством наших органов чувств.
Вместе с тем природа не знает бесконечно малых.  -образное задание начальных данных системы является идеализацией, безусловно, часто полезной. Идеализацией является и само понятие траектории. Согласно положениям квантовой механики, например, одновременное задание динамических переменных частиц, координат и импульсов возможно лишь с конечной точностью, определяемой соотношениями неопределенности Гейзенберга
-образное задание начальных данных системы является идеализацией, безусловно, часто полезной. Идеализацией является и само понятие траектории. Согласно положениям квантовой механики, например, одновременное задание динамических переменных частиц, координат и импульсов возможно лишь с конечной точностью, определяемой соотношениями неопределенности Гейзенберга
 ~
~ 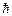 ,
,
где 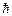 – постоянная Планка.
– постоянная Планка.
Фазовое пространство системы  частиц, таким образом, квантовано. Квантованность же в том или ином смысле фазового пространства приводит к идее нелокального описания системы. Наблюдаемая необратимость, следовательно, может быть связана с вынужденным объективно существующим огрублением описания, его нелокальностью.
частиц, таким образом, квантовано. Квантованность же в том или ином смысле фазового пространства приводит к идее нелокального описания системы. Наблюдаемая необратимость, следовательно, может быть связана с вынужденным объективно существующим огрублением описания, его нелокальностью.
Здесь есть и еще один аспект. Классическая механика основана на использовании концепции материальной точки. Строго говоря, о материальной точке можно говорить лишь как об изолированном объекте. Наличие в ее окрестности других взаимодействующих с ней материальных точек разрушает саму концепцию. По выражению А.А. Власова, классическая механика неявно использует допущение о том, что материальная точка никак не связана (топологически) с окружающими ее точками пространства. Таким образом, концепция системы взаимодействующих частиц требует их нелокальности. Можно сказать, что нелокальность порождается взаимодействием частиц. И. Пригожин приводит характерный пример взаимодействия электронов и фотонов. Гамильтоново описание такой системы (см. ч. II), при котором выделяются гамильтонианы изолированных частиц (электронов и фотонов) и их взаимодействия, является достаточно грубой идеализацией. Электромагнитное взаимодействие электронов с фотонами приводит к тому, что вокруг электрона образуется фотонная шуба. Как справедливо пишет И. Пригожин: «”Голый” элект-
рон – не более чем формальное понятие».
Нелокальность фазового пространства с необходимостью приводит к существованию флуктуаций. Поэтому адекватное описание системы большого числа взаимодействующих частиц принципиально требует учета протекающих в ней флуктуационных процессов. Статистический характер таких процессов делает описание системы еще более сложным. И мы приходим к выводу о том, что, во-первых, наблюдаемая необратимость является следствием внутренней микроскопической стохастичности и, во-вторых, построение адекватного описания системы многих частиц требует сочетания динамического и статистического описаний.
Наконец, следует упомянуть еще одно объяснение наблюдаемой необратимости, получившее достаточно широкое распространение в последние несколько десятилетий. Изучение неустойчивости фазовых траекторий в нелинейных физических системах привело, как мы видели, к развитию представлений о динамическом хаосе. Необратимость поведения системы связывается поэтому со стохастическим характером ее эволюции. Нам представляется, что здесь все-таки имеет место недоразумение. Действительно, перемешивающий характер движения системы означает только, что две фазовые траектории, стартуя из состояния, когда их начальные положения находятся как угодно близко (в 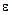 -окрестности,
-окрестности, 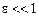 ), с течением времени могут разойтись сколь угодно далеко. Это положение иллюстрирует рисунок. Однако, если взаимодействия частиц в системе абсолютно упругие, то, обратив в момент времени
), с течением времени могут разойтись сколь угодно далеко. Это положение иллюстрирует рисунок. Однако, если взаимодействия частиц в системе абсолютно упругие, то, обратив в момент времени  направление времени (и, естественно, импульсов), система с необходимостью будет эволюционировать вдоль своих фазовых траекторий, отмеченных на рисунке пунктирными стрелками. Движение, таким образом, является обратимым!
направление времени (и, естественно, импульсов), система с необходимостью будет эволюционировать вдоль своих фазовых траекторий, отмеченных на рисунке пунктирными стрелками. Движение, таким образом, является обратимым!
Возникновению динамического описания системы многих частиц посредством дифференциальных уравнений мы обязаны великим И. Ньютону и Г.В. Лейбницу. Введение бесконечно малых и переход к соответствующим пределам позволили разрешить ряд парадоксов (типа апорий Зенона) и создать математически строгую основу описания таких систем. С приходом в науку дифференциальных уравнений воцарился детерминизм, в основе которого, с одной стороны, лежит предопределенность всего сущего, а с другой – обратимость. Насколько такой детерминизм соответствует реально наблюдаемым в природе процессам? Вопрос этот все еще не имеет исчерпывающего ответа. Однако следует отметить, что наблюдаемое поведение макроскопических систем необратимо и несимметрично, таким образом, относительно времени. Вопрос о том, как такую необратимость сочетать с динамикой составляющих систему частиц, является ключевым для понимания физики реально происходящих процессов[20]. Какой же ответ представляется сегодня нам наиболее адекватным?
|
| |  |
Эволюция системы многих взаимодействующих частиц
в фазовом пространстве: непрерывные стрелки – прямой
ход эволюции, пунктирные – эволюция при инверсии
времени
Прежде всего, следует отметить, что концепция теоретической механики родилась при изучении системы невзаимодействующих материальных точек. Кинематическое описание такой системы является полным, если удается задать координаты и скорости всех составляющих ее частиц. Собственно понятие траектории, являющееся основополагающим в классической механике, возможно лишь, если координаты и скорости системы материальных точек могут быть заданы  -функциями, т. е. абсолютно точно. При сколь угодно малой, но не нулевой погрешности задания начальных данных всегда существует такой промежуток времени, спустя который понятие траектории станет бессмысленным – положение системы на траектории (или фазовой траектории) станет неопределенным. Квантовая механика принципиально ставит предел возможному заданию кинематических переменных системы многих частиц, фазовое пространство системы квантовано. В этой связи необходимо отметить, что квантованность фазового пространства существует безотносительно к процессу измерения. Просто абсолютно точное одновременное задание скорости и импульса даже изолированной частицы является не более чем идеализацией. Идеализацией является поэтому и описание системы многих частиц посредством системы дифференциальных уравнений Ньютона.
-функциями, т. е. абсолютно точно. При сколь угодно малой, но не нулевой погрешности задания начальных данных всегда существует такой промежуток времени, спустя который понятие траектории станет бессмысленным – положение системы на траектории (или фазовой траектории) станет неопределенным. Квантовая механика принципиально ставит предел возможному заданию кинематических переменных системы многих частиц, фазовое пространство системы квантовано. В этой связи необходимо отметить, что квантованность фазового пространства существует безотносительно к процессу измерения. Просто абсолютно точное одновременное задание скорости и импульса даже изолированной частицы является не более чем идеализацией. Идеализацией является поэтому и описание системы многих частиц посредством системы дифференциальных уравнений Ньютона.
На наш взгляд, важен для понимания динамики системы взаимодействующих частиц сам процесс взаимодействия. Взаимодействие частиц является нелокальным процессом и принципиально флуктуационным. Такой характер взаимодействия радикально меняет поведение системы. Существование неустойчивости и перемешивания в системе большого числа частиц делает ее поведение при флуктуационном характере их взаимодействия необратимым. К этой проблеме тесно примыкает и другая, как объяснить реально наблюдаемую в системе частиц диссипацию, как такая диссипация соотносится с обратимым механистическим описанием? Позднее мы убедимся, что диссипативные эффекты – следствие имеющих место в системе флуктуационных процессов. Таким образом, необратимость и диссипативное поведение систем многих частиц являются проявлением имеющих место микрофлуктуаций.
Часть II. Модели, описываемые
Дифференциальными уравнениями
в частных производных
В этой части работы рассмотрены некоторые типичные модели различных природных и технологических процессов, основанные на использовании уравнений в частных производных. Конечно, подобных моделей очень много, и мы ограничились лишь наиболее распространенными, с одной стороны, и наиболее типичными, с другой. Причем предпочтение отдавалось моделям и уравнениям, ранее в обычных курсах не рассматривавшимся.
Эта часть начинается с изложения иерархии уровней и методов описания систем многих частиц. Большое место уделяется гамильтоновым моделям, дается понятие интегрируемых и неинтегрируемых систем. Затем обсуждаются многочастичное (дискретное) и полевое описания систем многих частиц (или произвольной системы со многими степенями свободы). Вводятся понятия ансамбля систем и функций распределения, формулируется теорема Лиувилля и выводится уравнение Лиувилля, а также выводятся управляющие уравнения для открытых систем.
На сегодня практически единственным методом микроскопического описания систем различной природы является метод молекулярной динамики. Изложению этого метода и анализу получающихся с его помощью результатов также уделено значительное место.
Последующие разделы посвящены обсуждению гидродинамических моделей. В частности, рассмотрены уравнения Эйлера и Навье – Стокса, модельные уравнения, описывающие диффузию, теплопроводность, конвекцию, распространение волн и солитонов. В заключение рассмотрены модели дисперсных жидкостей и неклассических жидкостей. Последний раздел посвящен методу вихревой динамики, еще одному методу прямого численного моделирования динамики жидкости.
Целью научных занятий должно быть
такое направление ума, чтобы он вы-
носил истинные суждения обо всех
встречающихся предметах.
Ренэ Декарт
Иерархия уровней описания
Систем многих частиц
Построение модели среды является исходным пунктом ее изучения и описания. Ясно, что модели могут быть различными. Эти различия обусловлены многими причинами. Во-первых, степенью подробности описания, которого хотелось бы достичь. Во-вторых, полнотой исходной информации. В-третьих, возможностями математического и экспериментального исследования данной системы. Этот перечень легко продолжить.
Строго говоря, в зависимости от степени подробности описания системы можно выделить три способа или, как принято говорить, уровня описания: микроскопический; кинетический; макроскопический. Соответственно можно говорить о микроскопических (в частности, молекулярных моделях), кинетических и макроскопических моделях данной системы. Системой мы здесь, как и раньше, называем любую совокупность многих взаимодействующих между собой элементов, в частности частиц.
Микроскопическими называются модели, основанные на микроскопических представлениях о строении вещества. Самой общей моделью такого типа является модель, в которой система изучается на уровне молекул или атомов[21]. В этом случае она рассматривается как смесь взаимодействующих молекул или атомов. Так как основной интерес для нас представляют макроскопические системы, как правило, движение составляющих такую систему молекул (атомов) можно описывать классически. Это, в частности, означает, что температуры, при которых рассматривается эволюция систем, не должны быть слишком низкими. В противном случае для описания нужно было бы использовать методы квантовой механики. В классической механике динамика  взаимодействующих частиц описывается системой уравнений Ньютона
взаимодействующих частиц описывается системой уравнений Ньютона
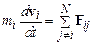 ,
, 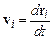 ,
, 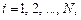 (7.1)
(7.1)
где  – сила взаимодействия частиц
– сила взаимодействия частиц  и
и  . При таком описании состояние системы в данный момент времени
. При таком описании состояние системы в данный момент времени 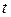 задается точкой в
задается точкой в 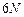 -мерном фазовом пространстве
-мерном фазовом пространстве  , которое обычно называется
, которое обычно называется 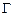 -пространством, где
-пространством, где  – импульс частицы
– импульс частицы  . Выполняя любой эксперимент, мы не можем сказать, какому состоянию в
. Выполняя любой эксперимент, мы не можем сказать, какому состоянию в 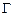 -пространстве соответствует данная экспериментальная реализация. Тем не менее, если результаты нескольких проведенных экспериментов одинаковы, то можно говорить, что различные состояния исследуемой системы или исследуемых систем, хотя и характеризуются разными начальными данными, в некотором смысле эквивалентны. Точнее, эквивалентны по результатам измерений. Таким образом, чтобы исследовать во времени поведение заданной системы частиц, можно изучать эволюцию некоторого набора тождественных систем
-пространстве соответствует данная экспериментальная реализация. Тем не менее, если результаты нескольких проведенных экспериментов одинаковы, то можно говорить, что различные состояния исследуемой системы или исследуемых систем, хотя и характеризуются разными начальными данными, в некотором смысле эквивалентны. Точнее, эквивалентны по результатам измерений. Таким образом, чтобы исследовать во времени поведение заданной системы частиц, можно изучать эволюцию некоторого набора тождественных систем
 частиц, различающихся начальными фазовыми состояниями. Такой набор систем был назван Дж. Гиббсом ансамблем. Каждой системе соответствует точка в фазовом пространстве (представляющая точка), а ансамблю – совокупность таких представляющих точек. Будем предполагать число этих точек достаточно большим, чтобы можно было ввести функцию плотности
частиц, различающихся начальными фазовыми состояниями. Такой набор систем был назван Дж. Гиббсом ансамблем. Каждой системе соответствует точка в фазовом пространстве (представляющая точка), а ансамблю – совокупность таких представляющих точек. Будем предполагать число этих точек достаточно большим, чтобы можно было ввести функцию плотности 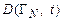 представляющих точек в фазовом пространстве, такую, что
представляющих точек в фазовом пространстве, такую, что  есть число представляющих точек системы в объеме
есть число представляющих точек системы в объеме 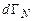 около точки
около точки 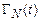 в момент времени
в момент времени 
С плотностью представляющих точек тесно связана  -час-тичная функция распределения
-час-тичная функция распределения 
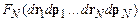 . Эта функция определяется так, что
. Эта функция определяется так, что 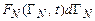 есть вероятность нахождения системы в момент времени t в элементе фазового объема
есть вероятность нахождения системы в момент времени t в элементе фазового объема 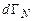 вблизи точки
вблизи точки 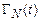 . По смыслу найденной таким образом функции распределения она должна быть нормирована на единицу
. По смыслу найденной таким образом функции распределения она должна быть нормирована на единицу
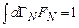 , (7.2)
, (7.2)
где интегрирование ведется по всему объему 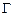 -пространства. Если все
-пространства. Если все  частиц тождественны, то функция распределения симметрична относительно перестановки фазовых координат частиц.
частиц тождественны, то функция распределения симметрична относительно перестановки фазовых координат частиц.
Описание системы многих частиц с помощью набора динамических переменных, удовлетворяющих уравнениям (7.1), или, что эквивалентно, с помощью  -частичной функции распределения является максимально подробным, однако сложности такого описания очевидны. Прежде всего, любая макроскопическая система состоит из огромного числа частиц, так что решить соответствующую систему уравнений не под силу самой быстродействующей вычислительной машине. Как же описывать такую систему? На помощь приходит концепция сокращения уровня описания системы, давно и с успехом использующаяся для исследования макроскопических систем. Яркий пример применения сокращения описания являет собой термодинамика, в которой система большого числа частиц описывается набором лишь нескольких переменных. В явном виде идея сокращения уровня описания была сформулирована Н.Н. Боголюбовым. Суть ее состоит в том, что на определенных стадиях эволюция системы может быть описана с помощью так называемых s- частичных функций распределения
-частичной функции распределения является максимально подробным, однако сложности такого описания очевидны. Прежде всего, любая макроскопическая система состоит из огромного числа частиц, так что решить соответствующую систему уравнений не под силу самой быстродействующей вычислительной машине. Как же описывать такую систему? На помощь приходит концепция сокращения уровня описания системы, давно и с успехом использующаяся для исследования макроскопических систем. Яркий пример применения сокращения описания являет собой термодинамика, в которой система большого числа частиц описывается набором лишь нескольких переменных. В явном виде идея сокращения уровня описания была сформулирована Н.Н. Боголюбовым. Суть ее состоит в том, что на определенных стадиях эволюция системы может быть описана с помощью так называемых s- частичных функций распределения
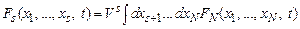 , (7.3)
, (7.3)
где 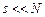 ;
;  ;
; 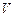 – объем системы.
– объем системы.
Функция (7.3) описывает динамику изолированной группы
s -частиц. В частности, при s = 1 мы имеем одночастичную функцию распределения, при s = 2 – двухчастичную и т. д. Если система может быть описана полным образом с помощью одночастичной функции распределения 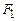 , говорят о кинетическом уровне ее описания. Одночастичная функция распределения определяет вероятность нахождения в момент времени t одной частицы в элементе фазового пространства
, говорят о кинетическом уровне ее описания. Одночастичная функция распределения определяет вероятность нахождения в момент времени t одной частицы в элементе фазового пространства  в окрестности точки
в окрестности точки 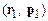 . Для тождественных частиц[22], молекул, удобно использовать одночастичную функцию, нормированную на число частиц в системе
. Для тождественных частиц[22], молекул, удобно использовать одночастичную функцию, нормированную на число частиц в системе
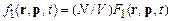 . (7.4)
. (7.4)
Тогда функция 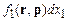 определяет число молекул в элементе объема
определяет число молекул в элементе объема 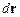 в окрестности точки
в окрестности точки  , имеющих импульсы, лежащие в интервале
, имеющих импульсы, лежащие в интервале  около значения
около значения 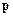 .
.
Одночастичная функция распределения удовлетворяет некоторым кинетическим уравнениям, построением и решением которых занимается кинетическая теория. Кинетическое описание системы многих частиц также является обычно излишне подробным. Кроме того, и вывод, и решение кинетических уравнений представляют собой очень непростые задачи, решение которых удается получить лишь в некоторых специальных случаях.
На практике при изучении макроскопической системы мы получаем экспериментальную информацию лишь о небольшом числе ее параметров, характеризующих систему в целом. Эти параметры принято называть макроскопическими переменными, а соответствующий уровень описания – макроскопическим. В газовой динамике и гидродинамике такой метод описания называется обычно гидродинамическим (газодинамическим), а соответствующие параметры – гидродинамическими переменными.
 Каждый уровень описания имеет свою область применимости, выбор набора макроскопических переменных часто неоднозначен. Использование той или иной модели для описания системы определяется этапами ее эволюции, которая в свою очередь зависит от соотношений между размерами внутренних структурных элементов среды и характерными масштабами всей системы.
Каждый уровень описания имеет свою область применимости, выбор набора макроскопических переменных часто неоднозначен. Использование той или иной модели для описания системы определяется этапами ее эволюции, которая в свою очередь зависит от соотношений между размерами внутренних структурных элементов среды и характерными масштабами всей системы.
Это научная поэма.
Уильям Роуэн Гамильтон [23]
Красота есть истина,
а истина – красота.
Джон Китс
Гамильтоновы системы
Уравнения Гамильтона
Динамика любой макроскопической системы, состоящей из большого числа частиц, атомов, молекул, ионов, кристаллов, описывается системой уравнений Ньютона (7.1). Широкий класс сил взаимодействия частиц, в частности взаимодействия атомов и молекул, можно представить в виде градиента некоторой скалярной функции 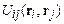 :
:
 , (8.1)
, (8.1)
которая называется потенциалом или потенциальной энергией взаимодействия частиц i и j. Эта функция зависит только от конфигурации частиц и не зависит от их скоростей.
Если взаимодействие частиц потенциальное и определяется потенциалом взаимодействия
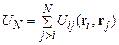 , (8.2)
, (8.2)
то полная энергия системы или, как говорят, ее гамильтониан в отсутствие внешнего поля имеет вид

|
|
|




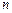 дифференциальных уравнений (5.2), которую можно записать в виде одного векторного уравнения
дифференциальных уравнений (5.2), которую можно записать в виде одного векторного уравнения
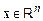 . (5.15)
. (5.15)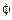 . Этот поток может иметь аттрактор
. Этот поток может иметь аттрактор 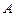 .
.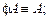 (ii)
(ii) 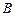 ненулевого объема, которая называется областью притяжения аттрактора.
ненулевого объема, которая называется областью притяжения аттрактора.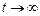 оказываются в
оказываются в 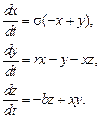 (5.16)
(5.16)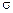 ,
, 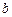 и
и 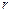 – некоторые постоянные. В экспериментах Э. Лоренца первые два параметра выбирались равными
– некоторые постоянные. В экспериментах Э. Лоренца первые два параметра выбирались равными 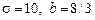 , а
, а 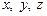 становится нерегулярной и очень чувствительна к изменению начальных условий. В экспериментах Э. Лоренца
становится нерегулярной и очень чувствительна к изменению начальных условий. В экспериментах Э. Лоренца 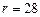 . Типичное поведение функции
. Типичное поведение функции 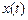 представлено на рис. 5.3. Здесь траекто-
представлено на рис. 5.3. Здесь траекто-

 взаимодействующих частиц (см. следующий раздел). Существуют, конечно, и другие важные отличия, но о них мы поговорим позднее.
взаимодействующих частиц (см. следующий раздел). Существуют, конечно, и другие важные отличия, но о них мы поговорим позднее.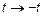 . При этом импульсы частиц также изменяют знак,
. При этом импульсы частиц также изменяют знак, 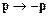 . Математически эта инвариантность связана с тем, что в уравнения Ньютона входят вторые производные от радиусов-векторов по времени. Уравнения механики, таким образом, инварианты относительно времени. Именно в этом смысле и уравнения механики описывают обратимые процессы. Отсюда, в частности, следует, что фазовые траектории прямого движения системы совпадают с фазовыми траекториями обращенного во времени движения. Но тогда со всей остротой встает вопрос, поставленный Дж. Николисом: «Как вообще возможна эволюция?» Действительно, эволюционное движение предполагает выделенность направления времени и неинвариантно относительно его обращения.
. Математически эта инвариантность связана с тем, что в уравнения Ньютона входят вторые производные от радиусов-векторов по времени. Уравнения механики, таким образом, инварианты относительно времени. Именно в этом смысле и уравнения механики описывают обратимые процессы. Отсюда, в частности, следует, что фазовые траектории прямого движения системы совпадают с фазовыми траекториями обращенного во времени движения. Но тогда со всей остротой встает вопрос, поставленный Дж. Николисом: «Как вообще возможна эволюция?» Действительно, эволюционное движение предполагает выделенность направления времени и неинвариантно относительно его обращения. -образное задание начальных данных системы является идеализацией, безусловно, часто полезной. Идеализацией является и само понятие траектории. Согласно положениям квантовой механики, например, одновременное задание динамических переменных частиц, координат и импульсов возможно лишь с конечной точностью, определяемой соотношениями неопределенности Гейзенберга
-образное задание начальных данных системы является идеализацией, безусловно, часто полезной. Идеализацией является и само понятие траектории. Согласно положениям квантовой механики, например, одновременное задание динамических переменных частиц, координат и импульсов возможно лишь с конечной точностью, определяемой соотношениями неопределенности Гейзенберга ~
~ 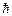 ,
,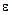 -окрестности,
-окрестности, 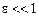 ), с течением времени могут разойтись сколь угодно далеко. Это положение иллюстрирует рисунок. Однако, если взаимодействия частиц в системе абсолютно упругие, то, обратив в момент времени
), с течением времени могут разойтись сколь угодно далеко. Это положение иллюстрирует рисунок. Однако, если взаимодействия частиц в системе абсолютно упругие, то, обратив в момент времени  направление времени (и, естественно, импульсов), система с необходимостью будет эволюционировать вдоль своих фазовых траекторий, отмеченных на рисунке пунктирными стрелками. Движение, таким образом, является обратимым!
направление времени (и, естественно, импульсов), система с необходимостью будет эволюционировать вдоль своих фазовых траекторий, отмеченных на рисунке пунктирными стрелками. Движение, таким образом, является обратимым!
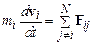 ,
, 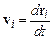 ,
, 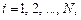 (7.1)
(7.1) – сила взаимодействия частиц
– сила взаимодействия частиц  и
и  . При таком описании состояние системы в данный момент времени
. При таком описании состояние системы в данный момент времени 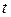 задается точкой в
задается точкой в 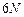 -мерном фазовом пространстве
-мерном фазовом пространстве  , которое обычно называется
, которое обычно называется 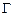 -пространством, где
-пространством, где  – импульс частицы
– импульс частицы 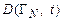 представляющих точек в фазовом пространстве, такую, что
представляющих точек в фазовом пространстве, такую, что  есть число представляющих точек системы в объеме
есть число представляющих точек системы в объеме 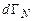 около точки
около точки 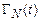 в момент времени
в момент времени 

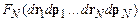 . Эта функция определяется так, что
. Эта функция определяется так, что 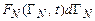 есть вероятность нахождения системы в момент времени t в элементе фазового объема
есть вероятность нахождения системы в момент времени t в элементе фазового объема 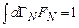 , (7.2)
, (7.2)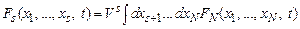 , (7.3)
, (7.3)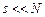 ;
;  ;
; 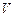 – объем системы.
– объем системы.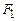 , говорят о кинетическом уровне ее описания. Одночастичная функция распределения определяет вероятность нахождения в момент времени t одной частицы в элементе фазового пространства
, говорят о кинетическом уровне ее описания. Одночастичная функция распределения определяет вероятность нахождения в момент времени t одной частицы в элементе фазового пространства  в окрестности точки
в окрестности точки 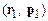 . Для тождественных частиц[22], молекул, удобно использовать одночастичную функцию, нормированную на число частиц в системе
. Для тождественных частиц[22], молекул, удобно использовать одночастичную функцию, нормированную на число частиц в системе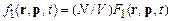 . (7.4)
. (7.4)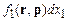 определяет число молекул в элементе объема
определяет число молекул в элементе объема 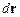 в окрестности точки
в окрестности точки  , имеющих импульсы, лежащие в интервале
, имеющих импульсы, лежащие в интервале  около значения
около значения 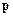 .
. Каждый уровень описания имеет свою область применимости, выбор набора макроскопических переменных часто неоднозначен. Использование той или иной модели для описания системы определяется этапами ее эволюции, которая в свою очередь зависит от соотношений между размерами внутренних структурных элементов среды и характерными масштабами всей системы.
Каждый уровень описания имеет свою область применимости, выбор набора макроскопических переменных часто неоднозначен. Использование той или иной модели для описания системы определяется этапами ее эволюции, которая в свою очередь зависит от соотношений между размерами внутренних структурных элементов среды и характерными масштабами всей системы.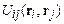 :
: , (8.1)
, (8.1)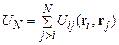 , (8.2)
, (8.2)


