Рассмотрим совокупность векторов 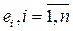 , линейного векторного пространства Х. Под линейной комбинацией этих векторов понимается вектор
, линейного векторного пространства Х. Под линейной комбинацией этих векторов понимается вектор
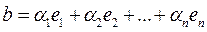 ,
,  ,
,
где 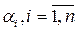 , - произвольные вещественные числа,
, - произвольные вещественные числа, 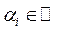 ,
, 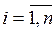 .
.
Когда все числа 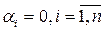 , то вектор
, то вектор 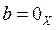 . Если в Х выбрать некоторое множество, состоящее из векторов
. Если в Х выбрать некоторое множество, состоящее из векторов 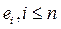 , этого пространства, то получим подпространство
, этого пространства, то получим подпространство 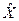 в Х, которое порождается этим множеством векторов. Если это подпространство совпадает с самим пространством Х, то говорят, что такое множество векторов порождает само пространство Х. В этом случае любой вектор из Х является линейной комбинацией этого множества векторов и при этом вектор-нуль
в Х, которое порождается этим множеством векторов. Если это подпространство совпадает с самим пространством Х, то говорят, что такое множество векторов порождает само пространство Х. В этом случае любой вектор из Х является линейной комбинацией этого множества векторов и при этом вектор-нуль 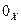 всегда принадлежит подпространству
всегда принадлежит подпространству 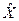 . Например, система векторов
. Например, система векторов 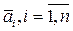 , порождает арифметическое пространства А n и представляет любой вектор
, порождает арифметическое пространства А n и представляет любой вектор 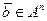 в виде линейной комбинации:
в виде линейной комбинации:
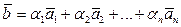 ,
,
этих векторов, где 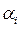 - вещественные числа. Множество всех линейных комбинаций
- вещественные числа. Множество всех линейных комбинаций 
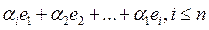 , векторов
, векторов 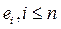 , линейного подпространства
, линейного подпространства 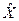 в Х называется линейной оболочкой этих векторов
в Х называется линейной оболочкой этих векторов 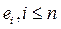 .
.
Примером линейного подпространства является множество матриц вида
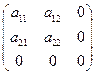 ,
, 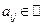 ,
,
в линейном пространстве матриц 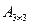 .
.
В линейном арифметическом пространстве А n совокупность всех решений ОСЛАУ (1.4) является подпространством пространства А n и его размерность, в силу Теоремы 1.5, равна числу k = n - r, где r – ранг матрицы данной ОСЛАУ.
Определение1.7. Векторы  , из векторного пространства Х называют линейно независимыми, если равенство
, из векторного пространства Х называют линейно независимыми, если равенство



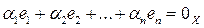 (1.7)
(1.7)
выполняется тогда и только тогда, когда все числа 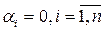 . В противном случае, если равенство (1.7) выполняется, когда среди чисел
. В противном случае, если равенство (1.7) выполняется, когда среди чисел 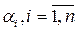 , существует хотя бы одно число
, существует хотя бы одно число 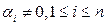 , векторы
, векторы  , называют линейно зависимыми. Если векторы
, называют линейно зависимыми. Если векторы  , линейно зависимы, то один из них является линейной комбинацией остальных векторов. Например, если в (1.7) число
, линейно зависимы, то один из них является линейной комбинацией остальных векторов. Например, если в (1.7) число 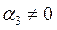 , то имеет место равенство
, то имеет место равенство
 . (1.7)*
. (1.7)*
Определение2.7. В общем случае некоторое векторное пространство X называется конечномерным, а число n его размерностью, если в этом пространстве существуют n линейно независимых вектора, а любые n + 1 векторов из этого пространства являются линейно зависимыми. Если же в векторном пространстве X имеется линейно независимая система из любого числа векторов, то такое пространство называют бесконечномерным.
Определение3.7. Система из n линейно независимых векторов  , в n - мерном векторном пространстве
, в n - мерном векторном пространстве 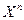 называется базисом этого пространства.
называется базисом этого пространства.
Если  - произвольный вектор в
- произвольный вектор в 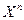 , то векторы
, то векторы  и базисные векторы
и базисные векторы  , линейно зависимы в
, линейно зависимы в 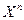 , т.к. число их равно n + 1, и потому справедливо равенство вида
, т.к. число их равно n + 1, и потому справедливо равенство вида
 =
= 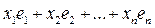 . (2.7)
. (2.7)
Вещественные числа  , однозначно определяются заданием вектора
, однозначно определяются заданием вектора  и базиса
и базиса 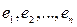 . В самом деле, пусть наряду с (2.7) имеется другое разложение вектора
. В самом деле, пусть наряду с (2.7) имеется другое разложение вектора  по базису
по базису 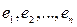 :
:
 =
= 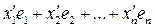 . (3.7)
. (3.7)
Вычитая из (2.7) равенство (3.7), получим равенство:
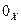 =
= 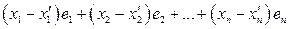 ,
,
откуда в силу линейной независимости векторов  , базиса пространства
, базиса пространства 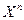 получаем равенства
получаем равенства  =
= 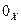 ,
, 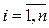 , т.е.
, т.е. 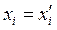 ,
, 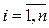 .
.
Числа 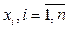 , называют координатами вектора
, называют координатами вектора  в базисе
в базисе 
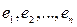 векторного пространства
векторного пространства 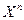 , а слагаемые в правой части равенства (2.7) компонентами этого вектора
, а слагаемые в правой части равенства (2.7) компонентами этого вектора  .
.
Замечание1.7. Рассмотрим векторы 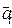 = (a 1 i, a 2 i,…, a ni), i = 1, 2,…, n, в А n и запишем для них равенство (1.7).Оно равносильно ОСЛАУ вида
= (a 1 i, a 2 i,…, a ni), i = 1, 2,…, n, в А n и запишем для них равенство (1.7).Оно равносильно ОСЛАУ вида

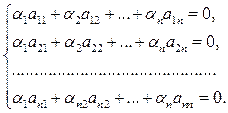 (4.7)
(4.7)
Однородная система (4.7) имеет единственное нулевое решение 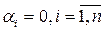 ,
,
тогда и только тогда, когда её определитель

(5.7)
Таким образом, неравенство (5.7) даёт условие линейной независимости векторов 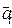 = (a 1 i, a 2 i,…, a ni), i = 1, 2,…, n, пространства А n ..и, наоборот, если
= (a 1 i, a 2 i,…, a ni), i = 1, 2,…, n, пространства А n ..и, наоборот, если 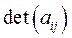 = 0, то ОСЛАУ (4.7) имеет хотя бы одно решение
= 0, то ОСЛАУ (4.7) имеет хотя бы одно решение  , и значит эти векторы линейно зависимы.
, и значит эти векторы линейно зависимы.
Замечание 2.7. Из (1.7)* следует, что если два вектора 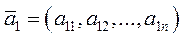 и
и 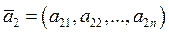 в пространстве А n линейно зависимы, то их координаты пропорциональны, т.е.
в пространстве А n линейно зависимы, то их координаты пропорциональны, т.е. 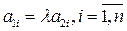 , где
, где 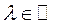 . Верно и обратное, что если
. Верно и обратное, что если
координаты этих векторов пропорциональны, то они линейно зависимы, например, векторы 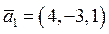 и
и 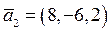 в А 3 линейно зависимы, потому что координаты их пропорциональны. Коэффициент их пропорциональности равен числу
в А 3 линейно зависимы, потому что координаты их пропорциональны. Коэффициент их пропорциональности равен числу 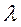 =2.
=2.
Замечание 3.7. Для любого векторного пространства 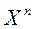 его размерность -число n совпадает с числом базисных векторов
его размерность -число n совпадает с числом базисных векторов 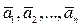 этого пространства.
этого пространства.
Замечание4.7. Пусть 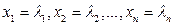 - какое – либо решение ОСЛАУ (1.4). Если записать его в виде вектора
- какое – либо решение ОСЛАУ (1.4). Если записать его в виде вектора 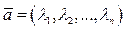 , то совокупность линейно независимых решений
, то совокупность линейно независимых решений 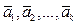 , где k = n - r, является фундаментальной системой решений (см. § 5), т.к. любое решение ОСЛАУ (1.4) можно представить в виде линейной комбинации этих векторов
, где k = n - r, является фундаментальной системой решений (см. § 5), т.к. любое решение ОСЛАУ (1.4) можно представить в виде линейной комбинации этих векторов 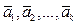 . Например, в примере 1.5 векторы
. Например, в примере 1.5 векторы
 =(14, 11,-2,1,0,0)
=(14, 11,-2,1,0,0)
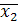 =(-4, -3, 0,0,1, 0)
=(-4, -3, 0,0,1, 0)
 =(1, 0, 1, 0, 0, 1)
=(1, 0, 1, 0, 0, 1)
могут быть приняты за базисные векторы подпространства решений, размерность которого равна числу k = n - r =6-3=3,т.к. они образуют фундаментальную систему решений для данной ОСЛАУ. Поэтому общее решение этой системы уравнений определяется вектором
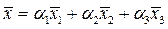 =
= 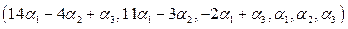 .
.
Замечание5.7. Из Замечания 2. 7 и формулы (6.6) следует, что два вектора 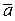 и
и 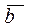 евклидова пространства E n линейно зависимы тогда и только тогда, когда для них выполняется равенство вида
евклидова пространства E n линейно зависимы тогда и только тогда, когда для них выполняется равенство вида  ,т.е. угол
,т.е. угол 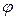 между
между 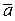 и
и 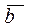 равен нулю. Поэтому линейно зависимые векторы
равен нулю. Поэтому линейно зависимые векторы 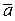 и
и 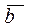 евклидова пространства E n , называют также параллельными и пишут
евклидова пространства E n , называют также параллельными и пишут 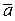

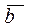 .
.
Замечание 6.7. В пространстве А n существует базис 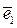 ,
, 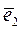 ,…,
,…, 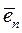 , составленный из единичных и взаимно ортогональных векторов
, составленный из единичных и взаимно ортогональных векторов 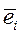 ,
, 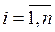 . Его называют ортонормированным базисом. Согласно Замечания1. 6 векторыортонормированный базиса в евклидовом пространстве E n можно выбрать с началом в точке О. Такой набор (О
. Его называют ортонормированным базисом. Согласно Замечания1. 6 векторыортонормированный базиса в евклидовом пространстве E n можно выбрать с началом в точке О. Такой набор (О 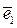 ,
, 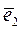 ,…,
,…, 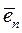 ) называют прямоугольной декартовой системой координат в E n с началом в точке О.
) называют прямоугольной декартовой системой координат в E n с началом в точке О.
Пример1.7. Разложить вектор  = (4,-15) по векторам
= (4,-15) по векторам 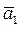 = (2,0),
= (2,0), 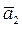 = (0,3) пространства А2 .
= (0,3) пространства А2 .
Решение. Согласно Замечание3.7 базис векторного пространства А2 состоит ровно из двух векторов. Покажем, что за базисные векторы в А2 можно взять эти данные векторы 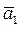 и
и 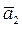 .Для этого надо установить, что они линейно независимы. Эти векторы будут линейно независимы, если для них выполняется равенство вида (1.7):
.Для этого надо установить, что они линейно независимы. Эти векторы будут линейно независимы, если для них выполняется равенство вида (1.7): 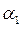
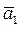 +
+ 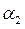
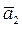 =
= 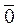 , когда оба числа
, когда оба числа 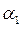 и
и 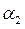 раны нулю одновременно. Запишем это равенство в матричном виде:
раны нулю одновременно. Запишем это равенство в матричном виде:
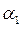
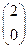 +
+ 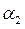
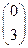 =
=  или
или 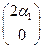 +
+ 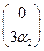 =
=  .
.
Используя правило сложения матриц, получим равенство
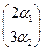 =
=  , откуда следует, что
, откуда следует, что 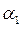 = 0 и
= 0 и 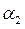 = 0.Следовательно, оба рассматриваемых вектора
= 0.Следовательно, оба рассматриваемых вектора 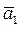 и
и 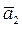 в векторном пространстве А2 линейно независимы и потому образуют базис в А2 .Разложим вектор
в векторном пространстве А2 линейно независимы и потому образуют базис в А2 .Разложим вектор  по этому базису
по этому базису 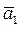 ,
, 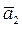 .Получим, что
.Получим, что  = =
= = 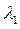
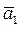 +
+ 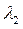
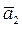 . Запишем это равенство в виде равенства векторов-столбцов:
. Запишем это равенство в виде равенства векторов-столбцов:
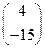 =
= 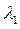
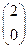 +
+ 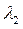
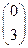 или
или 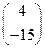 =
=  .
.
На основании определения равенства матриц получаем отсюда СЛАУ:
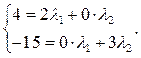
Решая эту систему линейных уравнений методом Крамера или Гаусса, получим
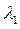 = 2,
= 2, 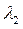 = -5, и потому искомое разложение вектора
= -5, и потому искомое разложение вектора  по данному базису
по данному базису
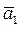 ,
, 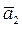 в векторном пространстве А2 имеет вид
в векторном пространстве А2 имеет вид  = 2
= 2 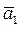 + (-5)
+ (-5) 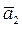 .
.
Линейную независимость данных векторов 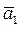 и
и 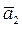 можно было установить и на основании Замечание1.7. Для этого необходимо вычислить определитель, составленный из координат этих векторов:
можно было установить и на основании Замечание1.7. Для этого необходимо вычислить определитель, составленный из координат этих векторов: 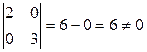 . Так как. этот определитель не равен нулю, то векторы
. Так как. этот определитель не равен нулю, то векторы 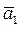 = (2,0),
= (2,0), 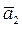 = (0,3) линейно независимы.
= (0,3) линейно независимы.
Пример2.7. Разложить элементы (векторы) линейного пространства Х многочленов первой степени 
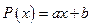 (см. пример 1.6) по его векторам
(см. пример 1.6) по его векторам 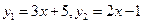 (геометрически они представляют собой две пересекающиеся прямые на координатной плоскости
(геометрически они представляют собой две пересекающиеся прямые на координатной плоскости  ).
).
Решение. Покажем вначале, что эти векторы линейно независимы. Для этого запишем для них равенство вида (1.7): 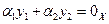 или
или 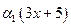 +
+ 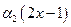 =
=
= 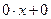 .Отсюда получим равенство
.Отсюда получим равенство 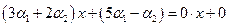 , которое выполняется для всех
, которое выполняется для всех  . Поэтому в силу теоремы алгебры о единственности многочленов получим систему равенств:
. Поэтому в силу теоремы алгебры о единственности многочленов получим систему равенств:
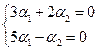
Из последнего уравнения находим,что 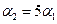 .Подставляя это значение для
.Подставляя это значение для 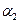 в первое уравнение, получим равенство 13
в первое уравнение, получим равенство 13 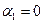 , откуда имеем
, откуда имеем 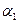 = 0 и значит и
= 0 и значит и 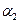 =0. А это означает в силу Определение 1 .7., что данные векторы
=0. А это означает в силу Определение 1 .7., что данные векторы 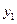 и
и 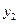 линейно независимы. Значит
линейно независимы. Значит 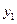 и
и 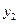 образуют базис в линейном пространстве Х многочленов первой степени и потому размерность этого пространства равна 2. Следовательно, любой вектор
образуют базис в линейном пространстве Х многочленов первой степени и потому размерность этого пространства равна 2. Следовательно, любой вектор 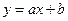 из Х можно на основании (2.7) разложить по векторам этого базиса:
из Х можно на основании (2.7) разложить по векторам этого базиса: 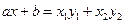 . Подставляя в это равенство вместо
. Подставляя в это равенство вместо 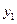 и
и 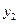 их выражения, получим равенство
их выражения, получим равенство 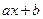 =
=  или
или
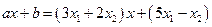 , которое выполняется для всех
, которое выполняется для всех  .Поэтому получим СЛАУ вида
.Поэтому получим СЛАУ вида 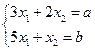 , которое имеет единственное решение
, которое имеет единственное решение  . Это координаты вектора
. Это координаты вектора 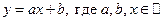 , в данном базисе
, в данном базисе 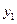 и
и 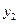 линейного пространства Х. Например, вектор
линейного пространства Х. Например, вектор 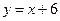 имеет координаты (1,-1), а вектор
имеет координаты (1,-1), а вектор  - координаты (2,0) в этом базисе.
- координаты (2,0) в этом базисе.
Рассмотрим два некоторые линейные пространства X и Y, элементы которых будем обозначать через x, y, z,… и 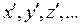 , соответственно.
, соответственно.
Определение4.7. Линейные пространства X и Y называют изоморфными, если между их элементами x, y и  можно установить взаимно однозначное соответствие
можно установить взаимно однозначное соответствие 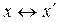 ;
; 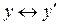 , при котором
, при котором 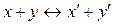 ,
, 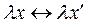 (
(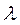 -любое вещественное число,
-любое вещественное число, 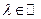 )
)
Если 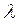 = 0, то получим, что
= 0, то получим, что 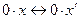 или
или 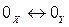 , т.е. при изоморфизме линейных пространств их нулевые элементы соответствуют друг другу.
, т.е. при изоморфизме линейных пространств их нулевые элементы соответствуют друг другу.
Справедливо
Утверждение1.7 Любые два изоморфных между собой пространства имеют одинаковое число базисных векторов, т. е. одну и ту же размерность.
Доказательство Понятие изоморфизма распространяется на любое конечное число элементов пространств X и Y:
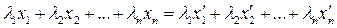 .
.
Отсюда следует, чтопри изоморфизме линейных пространств линейно независимые системывекторов одного пространства соответствуют линейно независимым системам векторов другого и, следовательно, любые два изоморфных между собой пространства имеют одинаковое число базисных векторов, т. е. одну и ту же размерность.
Верно и обратное
Утверждение 2.7. Любые два конечные линейные пространства 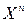 и
и 
одинаковой размерности n - изоморфны.
Доказательство. Достаточно установить изоморфизм для каждого из них, например для 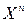 , с n -мерным арифметическим пространством А n .Пусть
, с n -мерным арифметическим пространством А n .Пусть
 - произвольный базис пространства
- произвольный базис пространства 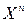 . Тогда каждый вектор
. Тогда каждый вектор 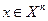 можно в силу (2.7) однозначно записать в виде
можно в силу (2.7) однозначно записать в виде
 =
= 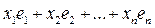 .
.
Поставим ему в соответствие вектор 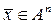 , который имеет те же координаты, что и вектор
, который имеет те же координаты, что и вектор 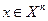 , т.е.
, т.е. 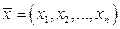 .Тогда получаем взаимно однозначное соответствие
.Тогда получаем взаимно однозначное соответствие 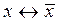 между элементами линейных векторных пространств А n и
между элементами линейных векторных пространств А n и 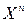 .Покажем, что это соответствие является изоморфизмом между А n и
.Покажем, что это соответствие является изоморфизмом между А n и 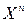 .Для этого возьмём ещё один вектор
.Для этого возьмём ещё один вектор 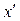 =
= 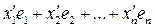 в пространстве
в пространстве 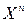 .Так как при сложении векторов в линейном пространстве
.Так как при сложении векторов в линейном пространстве 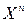 соответствующие их координаты складываются:
соответствующие их координаты складываются:
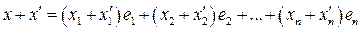 ,
,
а при умножении вектора 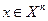 на вещественное число
на вещественное число 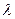 все координаты его умножаются на это число:
все координаты его умножаются на это число:
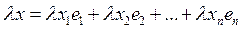 ,
,
то получим соответствия 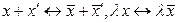 , т.е. между множествами всех элементов векторных пространств
, т.е. между множествами всех элементов векторных пространств 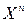 и А n установлено взаимно однозначное соответствие,сохраняющее линейные операции. А это означает, что
и А n установлено взаимно однозначное соответствие,сохраняющее линейные операции. А это означает, что 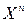 и А n изоморфны между собой.
и А n изоморфны между собой.
Из доказанных утверждений 1.7и 2.7 получается
Теорема 1.7. Для того чтобы два конечномерных векторных пространства были изоморфны между собой, необходимо и достаточно, чтобы они имели одну и ту же размерность.
Замечание 7.7. С помощью теоремы 1.7 легко устанавливается изоморфизм конечномерных векторных пространств. Из этой теоремы следует также, что с точностью до изоморфизма представляет интерес только одно какое либо n –векторное пространство, например, А n. Аксиоматическое определение линейного векторного пространства Х имеет преимущество в том,что оно непосредственно выделяет свойства векторов (элементов), которые не зависят от выбора базиса, например, равенство нулю всех координат вектора есть свойство самого вектора, не зависящее выбора базиса (см. замечание1.6).
Пример3.7. Установить изоморфизм линейных пространств R и 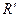 , приведённых в примере3.6.
, приведённых в примере3.6.
Решение. Так как 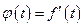 , то
, то 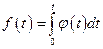 . Поэтому между элементами линейных пространств R и
. Поэтому между элементами линейных пространств R и 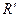 установлено взаимно однозначное соответствие, а с помощью равенств
установлено взаимно однозначное соответствие, а с помощью равенств  ,
, 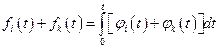 и
и
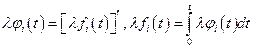 устанавливаются взаимно однозначные соответствия:
устанавливаются взаимно однозначные соответствия: 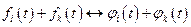 и
и 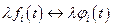 . А это означает, что R и
. А это означает, что R и 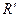 - изоморфные пространства.
- изоморфные пространства.
§8.Преобразование координат вектора при переходе к новому базису.
Рассмотрим в линейном пространстве А n два базиса: 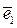 ,
, 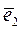 ,…,
,…, 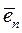 (старый) и
(старый) и 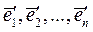 (новый). Выразим каждый вектор нового базиса через векторы старого базиса по формуле (2.7). Получим систему равенств:
(новый). Выразим каждый вектор нового базиса через векторы старого базиса по формуле (2.7). Получим систему равенств:
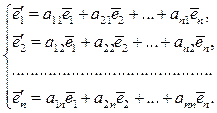
(1.8)
Матрица
S* = 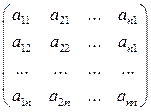
называется матрицей перехода от старого базиса к новому базису. Возьмём в пространстве А n любой вектор 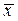 и запишем по формуле (2.7) его разложения по векторам старого и нового базиса:
и запишем по формуле (2.7) его разложения по векторам старого и нового базиса:
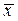 =
=  (2.8)
(2.8)
и
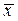 =
= 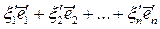 (3.8)
(3.8)
Из формул (2.8) и (3.8) получаем равенство вида
 =
= 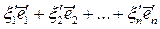 (4.8)
(4.8)
Подставляя в правую часть равенства (4.8) разложения 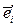 по векторам старого базиса по формулам (1.8), получим, в силу линейной независимости векторов старого базиса, формулы вида
по векторам старого базиса по формулам (1.8), получим, в силу линейной независимости векторов старого базиса, формулы вида
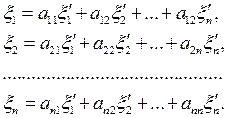 (5.8)
(5.8)
Формулы (5.8) называют формулами преобразования координат вектора 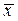 при переходе от старого базиса
при переходе от старого базиса 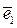 ,
, 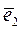 ,…,
,…, 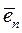 в пространстве А n к новому базису
в пространстве А n к новому базису 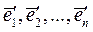 . Из формул (5.8) видно, что эти преобразования координат вектора
. Из формул (5.8) видно, что эти преобразования координат вектора 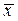 осуществляется при помощи матрицы S = (S *) T, столбцы которой являются координатами в формулах перехода (1.8) от старого базиса к новому базису.
осуществляется при помощи матрицы S = (S *) T, столбцы которой являются координатами в формулах перехода (1.8) от старого базиса к новому базису.
Если записать координаты вектора 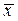 в старом и новом базисах в виде векторов – столбцов, то (5.8) можно кратко записать в матричной форме
в старом и новом базисах в виде векторов – столбцов, то (5.8) можно кратко записать в матричной форме
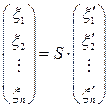 (5.9)
(5.9)
Пример1.7. Дан вектор 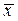 =
=  в линейном пространстве А4 .Найти разложение этого вектора по новому базису
в линейном пространстве А4 .Найти разложение этого вектора по новому базису 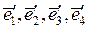 , если
, если
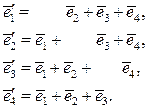
Решение. Выпишем матрицу перехода от старого базиса к новому базису:
S * = 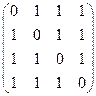
Столбцы этой матрицы являются коэффициентами в формулах (5.8) преобразования координат вектора 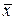 при переходе от старого базиса к новому базису. Поэтому получаем формулы преобразования координат этого вектора по формуле (5.9):
при переходе от старого базиса к новому базису. Поэтому получаем формулы преобразования координат этого вектора по формуле (5.9):
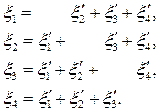 (6.8)
(6.8)
Так как по условию задачи имеем, что 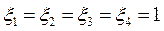 , то подставляя эти значения в правые части системы линейных алгебраических уравнений (6.8) и решив полученную СЛАУ, находим, что
, то подставляя эти значения в правые части системы линейных алгебраических уравнений (6.8) и решив полученную СЛАУ, находим, что  . Потому для вектора
. Потому для вектора 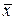 в новом базисе
в новом базисе 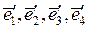 получим разложение вида
получим разложение вида
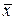 =
= 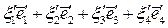 =
= 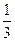

§9.Линейные преобразования (операторы).
Принимая во внимание, что все линейные пространства изоморфны арифметическому пространству А n (см. Замечание 7.7) , выберем для дальнейших рассуждений два конечных линейных пространства: А n размерности n и А m размерности m.
Определение 1.9. Если задан закон или правило, по которому каждому вектору 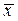 пространства : А n ставится в соответствие единственный вектор
пространства : А n ставится в соответствие единственный вектор 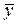 пространства А m, то говорят, что задан оператор (преобразование)
пространства А m, то говорят, что задан оператор (преобразование)  , действующий из А n в А m и пишут
, действующий из А n в А m и пишут 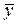 =
=  или
или 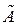 : А n
: А n 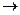 А m либо
А m либо 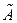
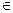
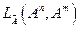 .
.
Вектор 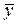 =
=  называется образом вектора
называется образом вектора 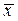 , а сам вектор
, а сам вектор 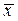 прообразом вектора
прообразом вектора 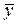 .
.
Определение 2.9. Оператор  называют линейным и пишут
называют линейным и пишут 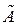
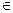
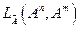 , если для любых двух векторов
, если для любых двух векторов 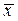 и
и 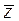 пространства : А n и любого действительного числа
пространства : А n и любого действительного числа 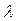 ,
, 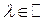 , выполняются соотношения:
, выполняются соотношения:
1. 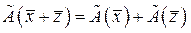 ;
;
2. 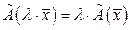 .
.
Линейное преобразование называется тождественным, если  =
= 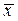 , т.е. оно любой вектор
, т.е. оно любой вектор 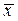 преобразует в самого себя. Тождественное линейное преобразование обозначается через Е. Таким образом Е
преобразует в самого себя. Тождественное линейное преобразование обозначается через Е. Таким образом Е 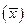 =
= 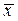 .
.
Замечание.1.9. Преобразование  =
= 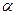

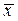 , где
, где 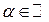 , является линейным. В самом деле, имеем
, является линейным. В самом деле, имеем 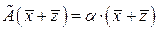 =
= 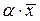 +
+ 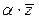 =
=  +
+ 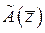 и
и
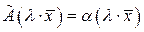 =
= 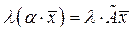 , т.е. оба условия, определяющие линейное преобразование, оказываются выполненными. Рассмотренное преобразование называется преобразованием подобия.
, т.е. оба условия, определяющие линейное преобразование, оказываются выполненными. Рассмотренное преобразование называется преобразованием подобия.
Рассмотрим СЛАУ вида (1.3):
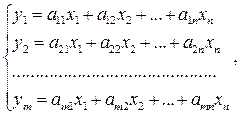
 (1.9)
(1.9)
которое задаёт линейное преобразование координат вектора 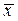 =
= 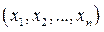
линейного пространства А n в координаты вектора 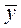 =
= 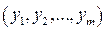 из пространства А m . Это преобразование задаётся матрицей
из пространства А m . Это преобразование задаётся матрицей
А=  =
=  = (а ij) (2.9)
= (а ij) (2.9)
с вещественными коэффициентами ajj ÎR.
Справедливо
Утверждение 1.9. Каждая матрица А= =  размера
размера 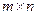 , определяемая таблицей (2.9) с вещественными коэффициентами, при заданных базисах в линейных пространствах А n и А m порождает линейное преобразование
, определяемая таблицей (2.9) с вещественными коэффициентами, при заданных базисах в линейных пространствах А n и А m порождает линейное преобразование 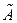
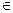
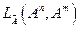 , действующее из А n в А m .
, действующее из А n в А m .
Доказательство. Выберем в линейном пространстве А n некоторый базис 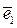 ,
, 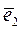 ,…,
,…, 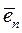 , а в А m произвольный базис
, а в А m произвольный базис 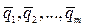 .Тогда преобразование (1.9) каждому вектору
.Тогда преобразование (1.9) каждому вектору 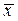 =
= 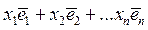 из А n даёт возможность сопоставить вектор
из А n даёт возможность сопоставить вектор 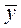 =
= 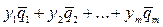 пространства А m , координаты которого
пространства А m , координаты которого 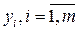 , вычисляются по формулам (1.9).А это означает, что преобразование (1.9), заданное матрицей (2.9), определяет некоторое отображение
, вычисляются по формулам (1.9).А это означает, что преобразование (1.9), заданное матрицей (2.9), определяет некоторое отображение 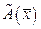 , которое относит вектору
, которое относит вектору 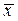 из А n вектор
из А n вектор 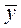 =
= 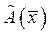 в пространстве А m . При этом оператор
в пространстве А m . При этом оператор 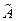 : А n
: А n  А m , как нетрудно видеть, обладает свойством линейности:
А m , как нетрудно видеть, обладает свойством линейности:
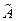
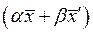 =
= 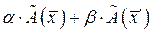
для любых векторов 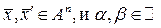 .
.
Замечание.2.9. Согласно формуле (2.3) линейное преобразование (1.9) можно записать в матричной форме
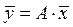 , (3.9)
, (3.9)
где слева стоит вектор-столбец 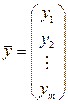 , а справа находится произведение матрицы А, заданной в виде таблицы (2.9), на вектор- столбец
, а справа находится произведение матрицы А, заданной в виде таблицы (2.9), на вектор- столбец  . В самом векторном равенстве
. В самом векторном равенстве 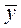 =
= 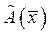 справа стоит образ элемента
справа стоит образ элемента 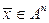 при действии на него отображения
при действии на него отображения 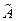 : А n
: А n 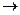 А m, т.е.
А m, т.е. 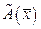
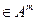 , а слева его краткое обозначение
, а слева его краткое обозначение 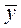 или равный ему элемент пространства
или равный ему элемент пространства 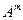 .
.
Верно и обратное
Утверждение2.9. Для произвольного линейного оператора 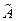



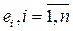 , линейного векторного пространства Х. Под линейной комбинацией этих векторов понимается вектор
, линейного векторного пространства Х. Под линейной комбинацией этих векторов понимается вектор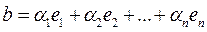 ,
, 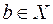 ,
,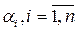 , - произвольные вещественные числа,
, - произвольные вещественные числа, 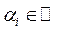 ,
, 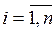 .
.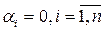 , то вектор
, то вектор 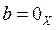 . Если в Х выбрать некоторое множество, состоящее из векторов
. Если в Х выбрать некоторое множество, состоящее из векторов 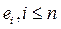 , этого пространства, то получим подпространство
, этого пространства, то получим подпространство 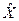 в Х, которое порождается этим множеством векторов. Если это подпространство совпадает с самим пространством Х, то говорят, что такое множество векторов порождает само пространство Х. В этом случае любой вектор из Х является линейной комбинацией этого множества векторов и при этом вектор-нуль
в Х, которое порождается этим множеством векторов. Если это подпространство совпадает с самим пространством Х, то говорят, что такое множество векторов порождает само пространство Х. В этом случае любой вектор из Х является линейной комбинацией этого множества векторов и при этом вектор-нуль 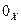 всегда принадлежит подпространству
всегда принадлежит подпространству 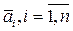 , порождает арифметическое пространства А n и представляет любой вектор
, порождает арифметическое пространства А n и представляет любой вектор 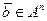 в виде линейной комбинации:
в виде линейной комбинации: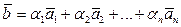 ,
,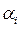 - вещественные числа. Множество всех линейных комбинаций
- вещественные числа. Множество всех линейных комбинаций 
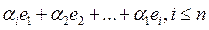 , векторов
, векторов 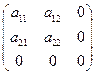 ,
,  ,
, .
. , из векторного пространства Х называют линейно независимыми, если равенство
, из векторного пространства Х называют линейно независимыми, если равенство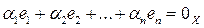 (1.7)
(1.7)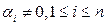 , векторы
, векторы 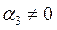 , то имеет место равенство
, то имеет место равенство . (1.7)*
. (1.7)*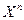 называется базисом этого пространства.
называется базисом этого пространства. - произвольный вектор в
- произвольный вектор в 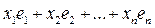 . (2.7)
. (2.7) , однозначно определяются заданием вектора
, однозначно определяются заданием вектора 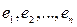 . В самом деле, пусть наряду с (2.7) имеется другое разложение вектора
. В самом деле, пусть наряду с (2.7) имеется другое разложение вектора 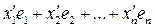 . (3.7)
. (3.7)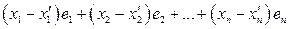 ,
, =
= 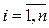 , т.е.
, т.е. 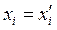 ,
, 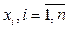 , называют координатами вектора
, называют координатами вектора 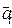 = (a 1 i, a 2 i,…, a ni), i = 1, 2,…, n, в А n и запишем для них равенство (1.7).Оно равносильно ОСЛАУ вида
= (a 1 i, a 2 i,…, a ni), i = 1, 2,…, n, в А n и запишем для них равенство (1.7).Оно равносильно ОСЛАУ вида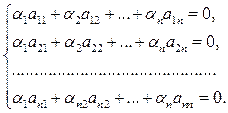 (4.7)
(4.7)
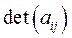 = 0, то ОСЛАУ (4.7) имеет хотя бы одно решение
= 0, то ОСЛАУ (4.7) имеет хотя бы одно решение  , и значит эти векторы линейно зависимы.
, и значит эти векторы линейно зависимы.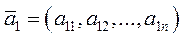 и
и 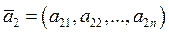 в пространстве А n линейно зависимы, то их координаты пропорциональны, т.е.
в пространстве А n линейно зависимы, то их координаты пропорциональны, т.е. 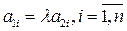 , где
, где 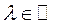 . Верно и обратное, что если
. Верно и обратное, что если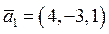 и
и 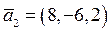 в А 3 линейно зависимы, потому что координаты их пропорциональны. Коэффициент их пропорциональности равен числу
в А 3 линейно зависимы, потому что координаты их пропорциональны. Коэффициент их пропорциональности равен числу 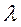 =2.
=2.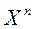 его размерность -число n совпадает с числом базисных векторов
его размерность -число n совпадает с числом базисных векторов 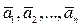 этого пространства.
этого пространства.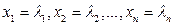 - какое – либо решение ОСЛАУ (1.4). Если записать его в виде вектора
- какое – либо решение ОСЛАУ (1.4). Если записать его в виде вектора 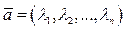 , то совокупность линейно независимых решений
, то совокупность линейно независимых решений 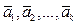 , где k = n - r, является фундаментальной системой решений (см. § 5), т.к. любое решение ОСЛАУ (1.4) можно представить в виде линейной комбинации этих векторов
, где k = n - r, является фундаментальной системой решений (см. § 5), т.к. любое решение ОСЛАУ (1.4) можно представить в виде линейной комбинации этих векторов  =(14, 11,-2,1,0,0)
=(14, 11,-2,1,0,0)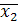 =(-4, -3, 0,0,1, 0)
=(-4, -3, 0,0,1, 0) =(1, 0, 1, 0, 0, 1)
=(1, 0, 1, 0, 0, 1) =
= 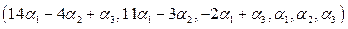 .
.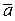 и
и 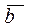 евклидова пространства E n линейно зависимы тогда и только тогда, когда для них выполняется равенство вида
евклидова пространства E n линейно зависимы тогда и только тогда, когда для них выполняется равенство вида  ,т.е. угол
,т.е. угол 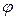 между
между 
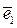 ,
, 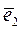 ,…,
,…, 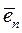 , составленный из единичных и взаимно ортогональных векторов
, составленный из единичных и взаимно ортогональных векторов 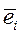 ,
, 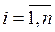 . Его называют ортонормированным базисом. Согласно Замечания1. 6 векторыортонормированный базиса в евклидовом пространстве E n можно выбрать с началом в точке О. Такой набор (О
. Его называют ортонормированным базисом. Согласно Замечания1. 6 векторыортонормированный базиса в евклидовом пространстве E n можно выбрать с началом в точке О. Такой набор (О  = (4,-15) по векторам
= (4,-15) по векторам 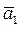 = (2,0),
= (2,0), 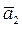 = (0,3) пространства А2 .
= (0,3) пространства А2 .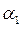
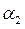
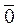 , когда оба числа
, когда оба числа 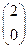 +
+ 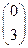 =
=  или
или 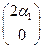 +
+ 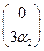 =
= 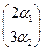 =
= 
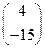 =
=  .
.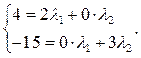
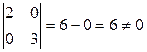 . Так как. этот определитель не равен нулю, то векторы
. Так как. этот определитель не равен нулю, то векторы  (см. пример 1.6) по его векторам
(см. пример 1.6) по его векторам 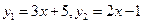 (геометрически они представляют собой две пересекающиеся прямые на координатной плоскости
(геометрически они представляют собой две пересекающиеся прямые на координатной плоскости 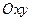 ).
).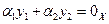 или
или 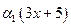 +
+ 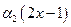 =
=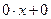 .Отсюда получим равенство
.Отсюда получим равенство 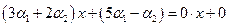 , которое выполняется для всех
, которое выполняется для всех  . Поэтому в силу теоремы алгебры о единственности многочленов получим систему равенств:
. Поэтому в силу теоремы алгебры о единственности многочленов получим систему равенств: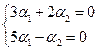
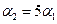 .Подставляя это значение для
.Подставляя это значение для 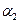 в первое уравнение, получим равенство 13
в первое уравнение, получим равенство 13 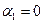 , откуда имеем
, откуда имеем 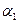 = 0 и значит и
= 0 и значит и 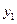 и
и 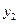 линейно независимы. Значит
линейно независимы. Значит 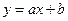 из Х можно на основании (2.7) разложить по векторам этого базиса:
из Х можно на основании (2.7) разложить по векторам этого базиса: 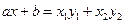 . Подставляя в это равенство вместо
. Подставляя в это равенство вместо 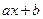 =
=  или
или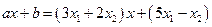 , которое выполняется для всех
, которое выполняется для всех 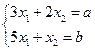 , которое имеет единственное решение
, которое имеет единственное решение  . Это координаты вектора
. Это координаты вектора 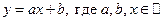 , в данном базисе
, в данном базисе 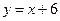 имеет координаты (1,-1), а вектор
имеет координаты (1,-1), а вектор  - координаты (2,0) в этом базисе.
- координаты (2,0) в этом базисе. , соответственно.
, соответственно. можно установить взаимно однозначное соответствие
можно установить взаимно однозначное соответствие 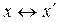 ;
; 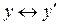 , при котором
, при котором 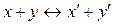 ,
, 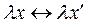 (
(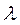 -любое вещественное число,
-любое вещественное число, 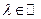 )
)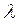 = 0, то получим, что
= 0, то получим, что 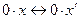 или
или 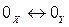 , т.е. при изоморфизме линейных пространств их нулевые элементы соответствуют друг другу.
, т.е. при изоморфизме линейных пространств их нулевые элементы соответствуют друг другу.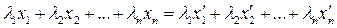 .
.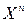 и
и 
 - произвольный базис пространства
- произвольный базис пространства 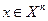 можно в силу (2.7) однозначно записать в виде
можно в силу (2.7) однозначно записать в виде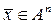 , который имеет те же координаты, что и вектор
, который имеет те же координаты, что и вектор 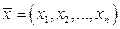 .Тогда получаем взаимно однозначное соответствие
.Тогда получаем взаимно однозначное соответствие 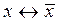 между элементами линейных векторных пространств А n и
между элементами линейных векторных пространств А n и 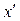 =
= 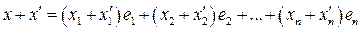 ,
,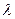 все координаты его умножаются на это число:
все координаты его умножаются на это число: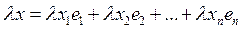 ,
,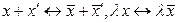 , т.е. между множествами всех элементов векторных пространств
, т.е. между множествами всех элементов векторных пространств 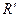 , приведённых в примере3.6.
, приведённых в примере3.6.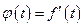 , то
, то 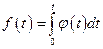 . Поэтому между элементами линейных пространств R и
. Поэтому между элементами линейных пространств R и  ,
, 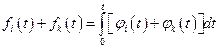 и
и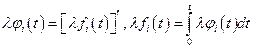 устанавливаются взаимно однозначные соответствия:
устанавливаются взаимно однозначные соответствия: 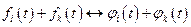 и
и 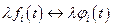 . А это означает, что R и
. А это означает, что R и 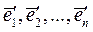 (новый). Выразим каждый вектор нового базиса через векторы старого базиса по формуле (2.7). Получим систему равенств:
(новый). Выразим каждый вектор нового базиса через векторы старого базиса по формуле (2.7). Получим систему равенств: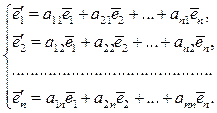
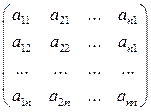
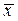 и запишем по формуле (2.7) его разложения по векторам старого и нового базиса:
и запишем по формуле (2.7) его разложения по векторам старого и нового базиса: (2.8)
(2.8)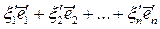 (3.8)
(3.8)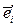 по векторам старого базиса по формулам (1.8), получим, в силу линейной независимости векторов старого базиса, формулы вида
по векторам старого базиса по формулам (1.8), получим, в силу линейной независимости векторов старого базиса, формулы вида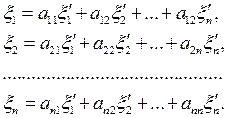 (5.8)
(5.8)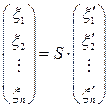 (5.9)
(5.9) в линейном пространстве А4 .Найти разложение этого вектора по новому базису
в линейном пространстве А4 .Найти разложение этого вектора по новому базису  , если
, если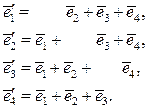
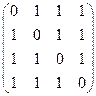
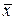 при переходе от старого базиса к новому базису. Поэтому получаем формулы преобразования координат этого вектора по формуле (5.9):
при переходе от старого базиса к новому базису. Поэтому получаем формулы преобразования координат этого вектора по формуле (5.9):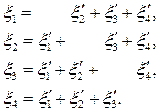 (6.8)
(6.8)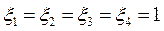 , то подставляя эти значения в правые части системы линейных алгебраических уравнений (6.8) и решив полученную СЛАУ, находим, что
, то подставляя эти значения в правые части системы линейных алгебраических уравнений (6.8) и решив полученную СЛАУ, находим, что  . Потому для вектора
. Потому для вектора 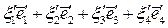 =
= 

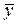 пространства А m, то говорят, что задан оператор (преобразование)
пространства А m, то говорят, что задан оператор (преобразование)  , действующий из А n в А m и пишут
, действующий из А n в А m и пишут 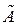 : А n
: А n 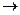 А m либо
А m либо 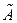
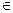
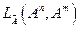 .
.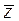 пространства : А n и любого действительного числа
пространства : А n и любого действительного числа 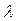 ,
, 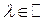 , выполняются соотношения:
, выполняются соотношения: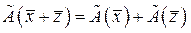 ;
;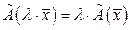 .
.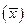 =
= 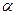

 , является линейным. В самом деле, имеем
, является линейным. В самом деле, имеем 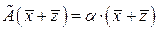 =
= 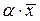 +
+ 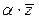 =
= 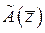 и
и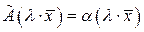 =
= 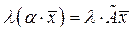 , т.е. оба условия, определяющие линейное преобразование, оказываются выполненными. Рассмотренное преобразование называется преобразованием подобия.
, т.е. оба условия, определяющие линейное преобразование, оказываются выполненными. Рассмотренное преобразование называется преобразованием подобия.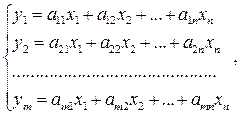
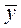 =
= 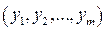 из пространства А m . Это преобразование задаётся матрицей
из пространства А m . Это преобразование задаётся матрицей =
=  = (а ij) (2.9)
= (а ij) (2.9)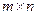 , определяемая таблицей (2.9) с вещественными коэффициентами, при заданных базисах в линейных пространствах А n и А m порождает линейное преобразование
, определяемая таблицей (2.9) с вещественными коэффициентами, при заданных базисах в линейных пространствах А n и А m порождает линейное преобразование 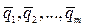 .Тогда преобразование (1.9) каждому вектору
.Тогда преобразование (1.9) каждому вектору 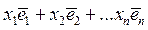 из А n даёт возможность сопоставить вектор
из А n даёт возможность сопоставить вектор 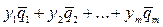 пространства А m , координаты которого
пространства А m , координаты которого 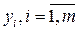 , вычисляются по формулам (1.9).А это означает, что преобразование (1.9), заданное матрицей (2.9), определяет некоторое отображение
, вычисляются по формулам (1.9).А это означает, что преобразование (1.9), заданное матрицей (2.9), определяет некоторое отображение 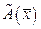 , которое относит вектору
, которое относит вектору 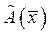 в пространстве А m . При этом оператор
в пространстве А m . При этом оператор 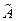 : А n
: А n 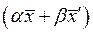 =
= 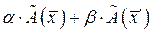
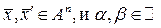 .
. 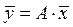 , (3.9)
, (3.9)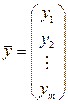 , а справа находится произведение матрицы А, заданной в виде таблицы (2.9), на вектор- столбец
, а справа находится произведение матрицы А, заданной в виде таблицы (2.9), на вектор- столбец  . В самом векторном равенстве
. В самом векторном равенстве 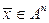 при действии на него отображения
при действии на него отображения 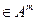 , а слева его краткое обозначение
, а слева его краткое обозначение 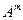 .
.

