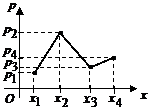ТЕОРИЯ ВЕРОЯТНОСТЕЙ (Лекции - 2016)
Комбинаторика
Перестановки
Пусть А – множество, состоящее из n различных элементов: А = { a 1, a 2, …, a n }. Всевозможные упорядоченные множества, которые можно получить из
неупорядоченного множества А, называются перестановками этого множества (или перестановками из n элементов).
Например, перестановками множества цифр {1, 2, 5} являются 6 трехзначных чисел:
125, 152, 215, 251, 512, 521.
Число перестановок из n элементов (обозначается P n) равно P n = 1 × 2 × … × n = n! .
По соглашению 0! = 1.
· На первом месте может быть любой из n элементов, на втором – любой из оставшихся n – 1 элементов, на третьем – любой из оставшихся n – 2 элементов и т.д. На последнем (n – м) месте будет один оставшийся элемент. Т.о., всего можно составить P n = n × (n – 1) × (n – 2) × … × 1 = n! перестановок из n элементов (рис.1).

Рис.1.
Пример 1. Сколько различных 5-значных чисел можно составить из цифр 0, 1, 2, 3, 4?
Всего из данных цифр можно составить P 5 = 5! различных 5- значных комбинаций. Но среди них есть такие, которые начинаются с нуля. Их надо исключить из рассмотрения. Чтобы их пересчитать, составим 4- значные комбинации из четырех цифр 1, 2, 3, 4. Таких комбинаций P 4 = 4!. Если теперь к каждой из этих комбинаций приписать впереди 0, то как раз и получим все те 5- значные комбинации, которые начинаются с 0. Исключая их, получим N = P 5 – P 4 = 5! – 4! = 120 – 24 = 96.
Размещения
Конечные упорядоченные подмножества, содержащие по m элементов, выбранных
из n элементов заданного множества, называются размещениями изn элементов поm.
Например, размещениями из 3 цифр {1, 2, 5} по 2 являются двузначных числа:
12, 15, 21, 25, 51, 52.
Число размещений изn элементов по m (обозначается 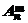 ) равно
) равно 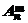 =
= 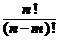 .
.
· На первом месте может быть любой из n элементов, на втором – любой из оставшихся n – 1 элементов, на третьем – любой из оставшихся n – 2 элементов и т.д. На m – м месте – любой из оставшихся n – m + 1 элементов. Т.о., всего можно составить 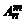 = n × (n – 1) × (n – 2) × … × (n – m + 1) размещений. Домножим числитель и знаменатель на (n – m)! и получим формулу числа размещений из n элементов по m:
= n × (n – 1) × (n – 2) × … × (n – m + 1) размещений. Домножим числитель и знаменатель на (n – m)! и получим формулу числа размещений из n элементов по m: 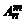 =
=  (рис.2).
(рис.2).
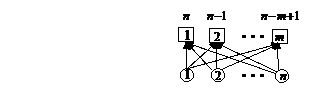
Рис.2.
Пример 2. Сколько различных 3-значных чисел можно составить из цифр 0, 1, 2, 3, 4?
Всего из данных цифр можно составить 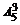 различных 3- значных комбинаций. Но среди них есть такие, которые начинаются с нуля. Их надо исключить из рассмотрения. Чтобы их пересчитать, составим 2- значные комбинации из четырех цифр 1, 2, 3, 4. Таких комбинаций
различных 3- значных комбинаций. Но среди них есть такие, которые начинаются с нуля. Их надо исключить из рассмотрения. Чтобы их пересчитать, составим 2- значные комбинации из четырех цифр 1, 2, 3, 4. Таких комбинаций  . Если теперь к каждой из этих комбинаций приписать впереди 0, то как раз и получим все те 3- значные комбинации, которые начинаются с 0. Исключая их, получим N =
. Если теперь к каждой из этих комбинаций приписать впереди 0, то как раз и получим все те 3- значные комбинации, которые начинаются с 0. Исключая их, получим N = 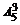 –
–  =
= 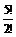 –
– 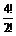 =
= 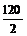 –
– 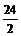 = 60 – 12 = 48.
= 60 – 12 = 48.
Сочетания
Конечные неупорядоченные множества, содержащие m различных элементов,
выбранные из n элементов заданного множества, называются сочетаниями изn элементов поm.
Например, из множества цифр {1, 2, 5} можно выбрать такие пары: { 1,2}, {1,5}, {2,5}.
Число сочетаний изn элементов поm (обозначается 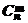 ) равно
) равно 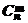 =
=  . · Среди множества всех размещений из n элементов по m каждые m элементов встречаются P m = m! раз (эти множества отличаются перестановками одних и тех же элементов). Объединяя данные множества в одно, получим формулу числа сочетаний из n элементов по m:
. · Среди множества всех размещений из n элементов по m каждые m элементов встречаются P m = m! раз (эти множества отличаются перестановками одних и тех же элементов). Объединяя данные множества в одно, получим формулу числа сочетаний из n элементов по m: 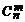 =
=  =
= 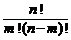 . ·
. ·
Пример 3. В корзине 8 различных фруктов. Сколькими способами можно вытащить 3 фрукта?
N = 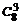 =
= 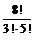 =
= 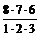 = 8 × 7 = 56.
= 8 × 7 = 56.
Перестановки с повторениями
Пусть А – некоторая совокупность, состоящая из n элементов m различных
типов (m ≤ n), причем элементы одного типа неразличимы между собой (пример: фрукты в корзине). Пусть k 1 элементов принадлежат 1-му типу, k 2 – 2-му, k 3 – 3-му, …, k m – m -му типу; при этом k 1 + k 2 + k 3 + … + k m = n. Например, если А = {1, 1, 2, 3, 1, 3}, то, считая элементами 1-го типа единицы, 2-го – двойки, 3-го – тройки, получим k 1 = 3, k 2 = 1, k 3 = 2.
Различные конечные совокупности, содержащие n элементов, из которых k 1 принадлежат 1-му типу, k 2 – 2-му, k 3 – 3-му, …, k m – m -му, называются перестановками с повторениями (кортежами), имеющими состав (спецификацию){ k 1, k 2, k 3, …, k m }.
Число различных перестановок с повторениями обозначается P n (k 1, k 2, k 3, …, k m) и равноP n (k 1, k 2, k 3, …, k m) = 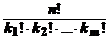 .
.
· Перенумеруем элементы внутри каждого типа. Тогда, считая все элементы различными, можно получить n! перестановок. Объединим все перестановки, отличающиеся только индексами элементов одного типа, в одну перестановку с повторениями (таких перестановок для элементов 1-го типа k 1!, для элементов 2-го типа k 2!, …, для элементов m -го типа k m!). Т.о., всего можно составить
P n (k 1, k 2, k 3, …, k m) = 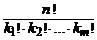 перестановок с повторениями из n элементов m типов. ·
перестановок с повторениями из n элементов m типов. ·
Пример 4. Сколько различных 6-значных чисел можно образовать из трех единиц, одной двойки и двух
троек?
N = P 6(3, 1, 2) = 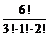 =
= 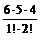 = 60.
= 60.
Сочетания с повторениями
Различные неупорядоченные совокупности, состоящие из n элементов, каждый из которых принадлежат одному из m типов, называются сочетаниями из m (различных) элементов по n элементов с повторениями.
Например, из трех различных элементов a 1, a 2, a 3 можно составить такие сочетания с повторениями:
(a 1, a 1), (a 1, a 2), (a 1, a 3), (a 2, a 2), (a 2, a 3), (a 3, a 3).
Число различных сочетаний с повторениями из m по n обозначается 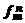 и равно
и равно
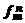 =
= 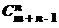 =
=  .
.
· Возьмем какое-нибудь сочетание из m по n. Запишем подряд столько единиц, сколько элементов 1-го типа в этом сочетании, затем поставим нуль; потом запишем столько единиц, сколько элементов 2-го типа, запишем нуль и т.д. Т.о. получим последовательность из n единиц и m – 1нулей (если элементов какого-либо типа нет, то единицы не пишем; нуль – граница между типами). Распределить n единиц на n + m – 1 мест можно 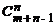 способами. Распределить m – 1 нулей на n + m – 1 мест можно
способами. Распределить m – 1 нулей на n + m – 1 мест можно 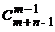 способами. ·
способами. ·
Пример 5. Сколько различных результатов бросаний можно получить при бросании двух кубиков?
N = 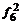 =
= 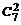 =
=  =
= 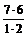 = 21.
= 21.
Размещения с повторениями
Любой упорядоченный набор m элементов множества А, содержащего n элементов, называется размещениями с повторениями из n элементов по m (возможно m > n).
Например, из двух различных элементов a 1, a 2 можно составить такие размещения по 3 с повторениями:
(a 1, a 1, a 1), (a 1, a 1, a 2), (a 1, a 2, a 1), (a 1, a 2, a 2), (a 2, a 1, a 1), (a 2, a 1, a 2), (a 2, a 2, a 1), (a 2, a 2, a 2).
Число различных размещений с повторениями из n по m обозначается 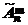 и равно
и равно
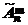 = n m .
= n m .
· На первом месте может быть любой из n элементов множества А, на втором – также любой из элементов множества А, то же и на третьем и т.д. Т.о., всего можно составить 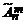 =
= 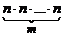 = n m. ·
= n m. ·
Пример 6. Кодовый замок открывается набором четырех цифр. Сколько различных запирающих
комбинаций у данного замка?
N = 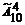 = 104. Действительно, первой, второй, третьей и четвертой цифрами может быть одна из 10
= 104. Действительно, первой, второй, третьей и четвертой цифрами может быть одна из 10
цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Следовательно, можно составить 10 × 10 × 10× 10 = 104 комбинаций.
Пример 7. Сколько различных трехбуквенных слов можно составить из 32 букв алфавита?
N =  = 323.
= 323.
Случайные события
Случайный опыт, или эксперимент, есть процесс, при котором возможны различные исходы, так что заранее нельзя предсказать результат. Опыт характеризуется тем, что его в принципе можно повторить сколько угодно раз. Возможные, исключающие друг друга, исходы опыта называются его элементарными событиями (исходами). Множество элементарных событий обозначается буквой Е.
Пример 1. Однократное бросание игральной кости. Множество Е состоит из шести элементарных
событий е 1, е 2, е 3, е 4, е 5, е 6, причем элементарное событие е i означает выпадение числа i.
Пример 2. Однократное бросание двух игральных костей. Множество Е состоит из 36 элементарных
событий е 11, е 12, …, е 66, причем элементарное событие е ij означает выпадение i очков на первой кости и j очков на второй.
Пример 3. Определение длительности служб прибора. Элементарными событиями здесь являются все положительные действительные числа, т.е.множество Е – вся положительная действительная полуось.
Помимо элементарных событий, часто встречаются события более сложной природы,
например, в случае игральных костей событие «выпадение четного числа» или в случае определения длительности службы прибора событие «длительность службы не менее 3000 часов».
Пусть осуществляется некоторый опыт, и пусть Е – множество его элементарных событий. Каждое подмножество А 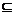 Е называется событием.
Е называется событием.






























 Событие А происходит тогда и только тогда, когда
Событие А происходит тогда и только тогда, когда
происходит одно из элементарных событий, из которых
состоит А.
Графически если элементарные события изобразить
точками на плоскости, то все точки – это Е, а точки внутри
замкнутой области А – событие А (рис.3).
Рис.3.
Пример 4. В примере 1 подмножество А = { е 2, е 4, е 6} образует событие А = «выпадение четного числа». В примере 2 подмножество В = { е 46, е 55, е 64} образует событие В = «сумма выпавших очков равна 10». В примере 3 подмножество С = {3000, +¥} можно интерпретировать как событие
С = «прибор служит не менее 3000 часов».
Т.к. Е состоит из всех элементарных событий, а при каждом опыте обязательно происходит одно из элементарных событий, то, т.о., Е происходит всегда; такое событие называется достоверным событием и также обозначается через Е. Пустое множество 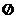 не содержит элементарных событий и, следовательно, никогда не происходит; такое событие называют невозможным событием и обозначают буквой U.
не содержит элементарных событий и, следовательно, никогда не происходит; такое событие называют невозможным событием и обозначают буквой U.




 Пусть А 1, А 2, …, А n – события, т.е. подмножества
Пусть А 1, А 2, …, А n – события, т.е. подмножества
некоторого множества Е элементарных событий. Тогда
объединение А 1 U А 2 U … U А n снова есть событие, т.к.
является подмножеством Е. Объединение А 1 U А 2 U … U А n а)

 происходит тогда и только тогда, когда происходит хотя бы
происходит тогда и только тогда, когда происходит хотя бы
одно из событий А 1, А 2, …, А n.
Событие А 1 U А 2 U … U А n называют суммой событий
А 1, А 2, …, А n. Его часто обозначают А 1 + А 2 + … + А n. б)
Графически сумма двух событий изображена на рис.4. Рис.4. А U В
Аналогично, пересечение А 1 ∩ А 2 ∩ … ∩ А n событий


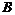
 А 1, А 2, …, А n снова есть некоторое событие. Пересечение
А 1, А 2, …, А n снова есть некоторое событие. Пересечение
А 1 ∩ А 2 ∩ … ∩ А n происходит тогда и только тогда, когда
происходят одновременно все события А 1, А 2, …, А n.
Событие А 1 ∩ А 2 ∩ … ∩ А n называют произведением
событий А 1, А 2, …, А n. Его часто обозначают А 1 А 2 … А n. Рис.5. А ∩ В
Графически произведение двух событий изображено на рис.5.
Пример 5. Пусть при определении длительности жизни прибора А 1 есть событие «продолжительность жизни лежит между 0 и t 1», а А 2 =«продолжительность жизни лежит между t 1 и t 2». Тогда А 1U А 2 есть событие «продолжительность жизни лежит между 0 и t 2».
Пример 6. Если при одновременном бросании двух костей А 1 есть событие «сумма очков ≥ 11», а
А 2 =«выпадает одинаковое количество очков», то А 1∩ А 2 есть событие «выпадает две шестерки».
Пример 7. Пусть в случае двух костей А 1=«сумма очков ≤ 2», а А 2 =«сумма очков ≥ 5». Тогда А 1∩ А 2 невозможное событие: А 1∩ А 2 = U.
Два события А 1 и А 2 называются несовместными, если А 1 ∩ А 2 = U,т.е. если событияА 1 и А 2 не могут произойти одновременно.
Если А – некоторое событие, то дополнение 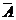 = Е \ A также является подмножеством Е, т.е. некоторым событием.
= Е \ A также является подмножеством Е, т.е. некоторым событием. 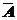 происходит тогда и только тогда, когда не происходит А.
происходит тогда и только тогда, когда не происходит А.
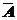 называется событием, противоположным (дополнительным) событию А. События А и
называется событием, противоположным (дополнительным) событию А. События А и 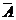 всегда несовместны:
всегда несовместны: 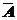 ∩ A = U.
∩ A = U.
Пример 8. Если при каком-нибудь измерении событие А =«измеренная величина ≥ а», то
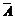 = «измеренная величина < а».
= «измеренная величина < а».
Пусть А 1, А 2, …, А n – попарно несовместные события (А i ∩ А j = U,  i ≠ j) и их сумма есть достоверное событие (А 1 + А 2 + … + А n = Е). Такое множество событий называется полной группой событий.
i ≠ j) и их сумма есть достоверное событие (А 1 + А 2 + … + А n = Е). Такое множество событий называется полной группой событий.
Для действий со случайными событиями (суммы, произведения, дополнения) справедливы формулы теории множеств:
A U B = B U A, A ∩ B = B ∩ A (коммутативность)
(A U B) U С = A U (B U С), (A ∩ B) ∩ С = A ∩ (B ∩ С) (ассоциативность)
(A U B) ∩ С = (A ∩ С) U (B ∩ С), (A ∩ B) U С = (A U С) ∩ (B U С) (дистрибутивность)

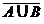 =
= 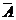 ∩
∩ 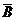 , A U B =
, A U B = 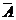 U
U 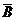 (формулы де Моргана)
(формулы де Моргана)
A U 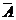 = Е, A ∩
= Е, A ∩ 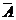 = U.
= U.
Аксиомы теории вероятностей
Пусть опыт повторяется n раз и при этом подсчитывается, как часто происходит интересующее нас событие. Допустим, что оно произошло m раз. Отношение  = W n (A) называется относительной частотой (или кратко частотой) случайного события А в
= W n (A) называется относительной частотой (или кратко частотой) случайного события А в
n опытах. При этом 0 ≤ W n (A) ≤ 1. Практика показывает, что при увеличении n частота стремится к некоторому постоянному значению. Вначале понятие вероятности случайного события пробовали определить как предел частоты. Это привело к трудностям, которые невозможно было преодолеть. В современной теории его считают основным понятием (как число, множество и т.д.), удовлетворяющим некоторым аксиомам.
Аксиомы теории вероятностей:
- Каждому случайному событию А поставлено в соответствие число Р (А), 0 ≤ Р (A) ≤ 1, называемое вероятностью события А.
- Вероятность достоверного события равна 1: Р (Е) = 1.
- Аксиома аддитивности: если А 1, А 2, …, А n – попарно несовместные события, т.е.
А i ∩ А j = U,  i ≠ j, то Р (
i ≠ j, то Р (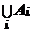 ) =
) =  .
.
На основании этих аксиом, в частности, получаем:
1 = Р (Е) = Р (Е U U) = Р (Е) + Р (U)= 1 + Р (U)=> Р (U) = 0 , т.е. вероятность
невозможного события равна нулю.
1 = Р (Е) = Р (А U 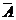 ) = Р (А) + Р (
) = Р (А) + Р (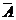 )=> Р (
)=> Р ( 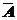 ) = 1 – Р (А) .
) = 1 – Р (А) .
Для произвольных (не обязательно попарно несовместных) случайных событий А 1, А 2, …, А n: Р (А 1 U А 2 U … U А n) ≤ 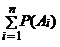 .
.
Геометрическая вероятность
Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка.
Если предположить, что вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L, то вероятность
попадания точки на отрезок l определяется равенством: Р =  .
.
Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу
брошена точка. Если предположить, что вероятность попадания точки на фигуру g пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно G, ни от формы g, то вероятность попадания точки на фигуру g определяется равенством:
Р = 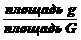 .
.
Аналогично определяется вероятность попадания точки в пространственную фигуру v,
которая составляет часть фигуры V: Р = 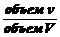 .
.
Пример 12. На отрезок ОА длины L числовой оси Ох наудачу брошены две точки: В (х) и С (у), причем
у ≥ х. Найти вероятность того, что длина отрезка ВС меньше длины отрезка ОВ.




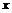
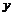
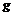


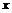
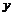
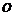
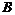
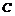
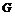
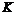
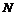
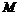
 Координаты точек В и С должны удовлетворять неравенствам
Координаты точек В и С должны удовлетворять неравенствам
0 ≤ х ≤ L,0 ≤ у ≤ L, у ≥ х. Введем в рассмотрение прямоугольную систему
координат Оху (рис. 6). В этой системе указанным неравенствам
удовлетворяют координаты любой точки, принадлежащей прямоугольному
треугольнику ОКМ. Т.о., этот треугольник можно рассматривать как
фигуру G, координаты точек которой представляют все возможные
значения координат точек В и С (прямоугольный треугольник ОКМ).
Длина отрезка ВС должна быть меньше длины отрезка ОВ, т.е. должно
иметь место неравенство у – х < x, или у < 2 x. Последнее неравенство Рис.6.
выполняется для координат всех точек фигуры g, которые лежат ниже
прямой у = 2 x (прямая ON). Все эти точки принадлежат треугольнику ONM. Т.о., этот треугольник можно рассматривать как фигуру g, координаты точек которой являются благоприятствующими интересующему нас событию (А = «длина отрезка ВС меньше длины отрезка ОВ»).
Искомая вероятность: площадь Р (А) =  =
= 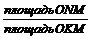 =
=  .
.
Распределение Пуассона
Распределение Пуассона получается в схеме Бернулли при большом числе испытаний n и малых значениях вероятности р появления события в каждом испытании (обычно достаточно выполнение условий: p < 0,1, npq < 10).
В вычислениях по формуле Бернулли при малых вероятностях р лучше пользоваться не приближенной формулой Лапласа (P n (k) = P k , n =  φ (x), где х =
φ (x), где х =  ), а
), а
приближенной формулой Пуассона при λ = np: P n (k) = p k , n = 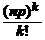 e – np .
e – np .
Пример. Для случайной величины Х, распределенной по закону Пуассона, вычислить Р (Х = m),
математическое ожидание и дисперсию, если λ = 0,3, m = 2.
P (X = 2) = 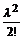 е –λ =
е –λ = 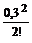 е – 0,3, M (X) = λ = 0,3, D (X) = λ = 0,3.
е – 0,3, M (X) = λ = 0,3, D (X) = λ = 0,3.
Пример. Проведены n независимых испытаний по схеме Бернулли. В каждом испытании может произойти событие А с вероятностью р. Подсчитать по формуле Пуассона вероятность того, что при этом событии А произошло m раз, если n = 1000, р = 0,002, m = 10.
P 1000(10)≈ P (X = 10) = 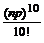 е – n p =
е – n p = 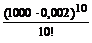 е – 2 =
е – 2 =  е – 2.
е – 2.
Отклонение относительной частоты от вероятности в
независимых испытаниях
Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность наступления события А равна р (0 < p < 1), абсолютная величина отклонения относительной частоты появления события А от вероятности наступления этого события не превышает положительного числа ε, равна удвоенной функции Лапласа при х = ε ×  :
:
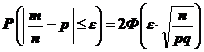 . (Ф
. (Ф 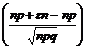 – Ф
– Ф  = Ф
= Ф 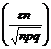 – Ф
– Ф 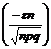 .
.
· | m – np | ≤ ε n => np – ε n ≤ m ≤ np + ε n. x ¢¢ = 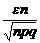 , x ¢ = –
, x ¢ = – 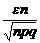 => P = 2 Ф
=> P = 2 Ф 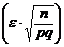 .
.
Пример 29. Вероятность появления события А в каждом из 625 испытаний р = 0,8. Найти вероятность того, что относительная частота появления данного события отклоняется от его вероятности по абсолютной величине не более чем на 0,04.
n = 625, p = 0,8, q = 0,2, ε =0,04 =>
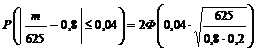 = 2 Ф (2,5) = || по таблице || = 2 × 0,4938 = 0,9876.
= 2 Ф (2,5) = || по таблице || = 2 × 0,4938 = 0,9876.
Пример 30. Проверяется на стандартность 900 деталей. Вероятность того, что деталь стандартна, р = 0,9. Найти с вероятностью 0,95 границы, в которых будет заключено число m стандартных деталей среди проверенных.
n = 900, p = 0,9, q = 0,1 => 2 Ф  = 0,95 или Ф (100 ε) = 0,475. Из таблицы получаем 0,475 = Ф (1,96) => 100 ε = 1,96 => ε ≈ 0,02. Т.о. с вероятностью 0,95 отклонение относительной частоты числа стандартных деталей от вероятности 0,9 удовлетворяет неравенству
= 0,95 или Ф (100 ε) = 0,475. Из таблицы получаем 0,475 = Ф (1,96) => 100 ε = 1,96 => ε ≈ 0,02. Т.о. с вероятностью 0,95 отклонение относительной частоты числа стандартных деталей от вероятности 0,9 удовлетворяет неравенству 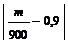 ≤, 0,02 или
≤, 0,02 или
0,88 ≤  ≤ 0,92. Т.о., искомое число m стандартных деталей среди 900 проверенных с вероятностью 0,95 заключено в границах 792 ≤ m ≤ 828.
≤ 0,92. Т.о., искомое число m стандартных деталей среди 900 проверенных с вероятностью 0,95 заключено в границах 792 ≤ m ≤ 828.
Наивероятнейшее число появления события
в независимых испытаниях
Число k 0 (наступления события А в n независимых испытаниях, в каждом из которых
вероятность наступления события А равна р (0 < p < 1)) называется наивероятнейшим числом появления события в n независимых испытаниях, если вероятность того, что событие наступит в этих испытаниях k 0 раз, превышает (или, по крайней мере, не меньше) вероятности остальных возможных исходов испытаний.
Наивероятнейшее число k 0 определяют из двойного неравенства np – q ≤ k 0 ≤ np + p. При этом:
а) если число np – q дробное, то существует одно наивероятнейшее число k 0;
б) если число np – q целое, то существуют два наивероятнейшее числа, а именно: k 0 и k 0 + 1;
в) если число np – целое, наивероятнейшее число k 0 = np.
Пример 31. Испытывается каждый из 15 элементов некоторого устройства. Вероятность того, что элемент выдержит испытание, равна р = 0,9. Найти наивероятнейшее число элементов, которые выдержат испытания.
n = 15, p = 0,9, q = 0,1 => 15 × 0,9 – 0,1 ≤ k 0 ≤ 15 × 0,9 + 0,9 или 13,4 ≤ k 0 ≤ 14,4 => k 0 = 14.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Случайной величиной называется действительная переменная, которая в зависимости от исходов опыта, т.е. в зависимости от случая, принимает различные (числовые) значения. Другими словами, случайной величиной называется функция, заданная на множестве исходов (элементарных событий) опыта.
Закон распределения
Законом распределения дискретной случайной величины называют перечень ее возможных значений (обычно расположенных в возрастающем порядке) и соответствующих им вероятностей.
Закон распределения дискретной случайной величины Х обычно задается в видетаблицы, 1-я строка которой содержит (в возрастающем порядке) возможные значения xi, а
2-я – вероятности pi:
| X
| x 1
| x 2
| …
| x n
|
| P
| p 1
| p 2
| …
| p n
|
Здесь 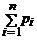 = 1. Если множество возможных значений Х бесконечно (но счётно), то ряд
= 1. Если множество возможных значений Х бесконечно (но счётно), то ряд
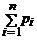 = p 1 + p 2 + … сходится и его сумма равна единице.
= p 1 + p 2 + … сходится и его сумма равна единице.
Закон распределения дискретной случайной величины Х также может быть задан аналитически (в виде формулы) P (X = x i) = φ (x i) или с помощью функции распределения (см. далее).
Закон распределения дискретной случайной
величины можно изобразить графически, для чего
в прямоугольной системе координат строят точки
М 1 (x 1, р 1), М 2 (x 1, р 1), …, М n (x n, р n) (x i – возможные
значения Х, p i – соответствующие вероятности) и
соединяют их отрезками прямых. Полученную фигуру Рис.12.
называют многоугольником распределения (рис.12).
Пример 1. Случайная величина Х задана своим законом распределения. Найти а.
0,4 + 0,1 + a = 1 ó a = 1 – 0,4 – 0,1 = 0,5.
<




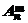 ) равно
) равно 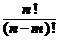 .
. = n × (n – 1) × (n – 2) × … × (n – m + 1) размещений. Домножим числитель и знаменатель на (n – m)! и получим формулу числа размещений из n элементов по m:
= n × (n – 1) × (n – 2) × … × (n – m + 1) размещений. Домножим числитель и знаменатель на (n – m)! и получим формулу числа размещений из n элементов по m:  (рис.2).
(рис.2). 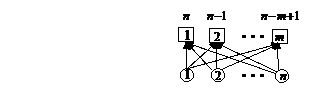
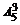 различных 3- значных комбинаций. Но среди них есть такие, которые начинаются с нуля. Их надо исключить из рассмотрения. Чтобы их пересчитать, составим 2- значные комбинации из четырех цифр 1, 2, 3, 4. Таких комбинаций
различных 3- значных комбинаций. Но среди них есть такие, которые начинаются с нуля. Их надо исключить из рассмотрения. Чтобы их пересчитать, составим 2- значные комбинации из четырех цифр 1, 2, 3, 4. Таких комбинаций  . Если теперь к каждой из этих комбинаций приписать впереди 0, то как раз и получим все те 3- значные комбинации, которые начинаются с 0. Исключая их, получим N =
. Если теперь к каждой из этих комбинаций приписать впереди 0, то как раз и получим все те 3- значные комбинации, которые начинаются с 0. Исключая их, получим N = 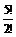 –
– 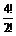 =
= 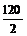 –
– 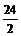 = 60 – 12 = 48.
= 60 – 12 = 48.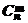 ) равно
) равно  . · Среди множества всех размещений из n элементов по m каждые m элементов встречаются P m = m! раз (эти множества отличаются перестановками одних и тех же элементов). Объединяя данные множества в одно, получим формулу числа сочетаний из n элементов по m:
. · Среди множества всех размещений из n элементов по m каждые m элементов встречаются P m = m! раз (эти множества отличаются перестановками одних и тех же элементов). Объединяя данные множества в одно, получим формулу числа сочетаний из n элементов по m: 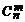 =
=  =
= 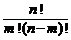 . ·
. ·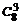 =
= 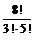 =
= 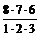 = 8 × 7 = 56.
= 8 × 7 = 56.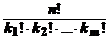 .
.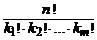 перестановок с повторениями из n элементов m типов. ·
перестановок с повторениями из n элементов m типов. ·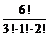 =
= 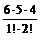 = 60.
= 60.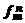 и равно
и равно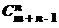 =
=  .
.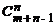 способами. Распределить m – 1 нулей на n + m – 1 мест можно
способами. Распределить m – 1 нулей на n + m – 1 мест можно 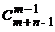 способами. ·
способами. ·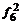 =
= 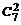 =
=  =
= 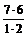 = 21.
= 21. и равно
и равно =
= 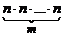 = n m. ·
= n m. ·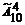 = 104. Действительно, первой, второй, третьей и четвертой цифрами может быть одна из 10
= 104. Действительно, первой, второй, третьей и четвертой цифрами может быть одна из 10  = 323.
= 323. 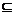 Е называется событием.
Е называется событием. 


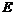
 Событие А происходит тогда и только тогда, когда
Событие А происходит тогда и только тогда, когда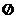 не содержит элементарных событий и, следовательно, никогда не происходит; такое событие называют невозможным событием и обозначают буквой U.
не содержит элементарных событий и, следовательно, никогда не происходит; такое событие называют невозможным событием и обозначают буквой U.

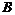

 происходит тогда и только тогда, когда происходит хотя бы
происходит тогда и только тогда, когда происходит хотя бы

 А 1, А 2, …, А n снова есть некоторое событие. Пересечение
А 1, А 2, …, А n снова есть некоторое событие. Пересечение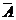 = Е \ A также является подмножеством Е, т.е. некоторым событием.
= Е \ A также является подмножеством Е, т.е. некоторым событием. 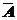 происходит тогда и только тогда, когда не происходит А.
происходит тогда и только тогда, когда не происходит А. 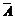 = «измеренная величина < а».
= «измеренная величина < а». i ≠ j) и их сумма есть достоверное событие (А 1 + А 2 + … + А n = Е). Такое множество событий называется полной группой событий.
i ≠ j) и их сумма есть достоверное событие (А 1 + А 2 + … + А n = Е). Такое множество событий называется полной группой событий.
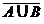 =
= 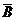 , A U B =
, A U B =  = W n (A) называется относительной частотой (или кратко частотой) случайного события А в
= W n (A) называется относительной частотой (или кратко частотой) случайного события А в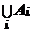 ) =
) =  .
.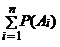 .
. .
.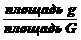 .
.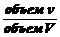 .
.



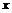
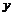
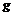

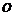
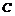
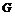
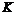
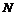
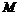
 =
= 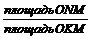 =
=  .
.  φ (x), где х =
φ (x), где х =  ), а
), а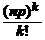 e – np .
e – np .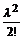 е –λ =
е –λ = 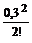 е – 0,3, M (X) = λ = 0,3, D (X) = λ = 0,3.
е – 0,3, M (X) = λ = 0,3, D (X) = λ = 0,3. 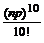 е – n p =
е – n p = 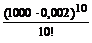 е – 2 =
е – 2 =  е – 2.
е – 2. :
: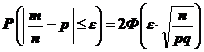 . (Ф
. (Ф 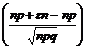 – Ф
– Ф  = Ф
= Ф 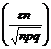 – Ф
– Ф 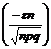 .
.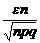 , x ¢ = –
, x ¢ = – 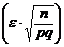 .
.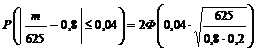 = 2 Ф (2,5) = || по таблице || = 2 × 0,4938 = 0,9876.
= 2 Ф (2,5) = || по таблице || = 2 × 0,4938 = 0,9876. = 0,95 или Ф (100 ε) = 0,475. Из таблицы получаем 0,475 = Ф (1,96) => 100 ε = 1,96 => ε ≈ 0,02. Т.о. с вероятностью 0,95 отклонение относительной частоты числа стандартных деталей от вероятности 0,9 удовлетворяет неравенству
= 0,95 или Ф (100 ε) = 0,475. Из таблицы получаем 0,475 = Ф (1,96) => 100 ε = 1,96 => ε ≈ 0,02. Т.о. с вероятностью 0,95 отклонение относительной частоты числа стандартных деталей от вероятности 0,9 удовлетворяет неравенству 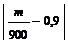 ≤, 0,02 или
≤, 0,02 или  ≤ 0,92. Т.о., искомое число m стандартных деталей среди 900 проверенных с вероятностью 0,95 заключено в границах 792 ≤ m ≤ 828.
≤ 0,92. Т.о., искомое число m стандартных деталей среди 900 проверенных с вероятностью 0,95 заключено в границах 792 ≤ m ≤ 828. 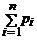 = 1. Если множество возможных значений Х бесконечно (но счётно), то ряд
= 1. Если множество возможных значений Х бесконечно (но счётно), то ряд