Биномиальное распределение (распределение Бернулли)
Биномиальным называют закон распределения дискретной случайной величины Х – числа появлений события А в n независимых испытаниях, в каждом из которых вероятность появления события А равна р. Вероятность возможного значения X = k (числа k появлений события А) вычисляется по формуле Бернулли
P n (k) = p k = P (X = k) =  pk (1 – p) n – k .
pk (1 – p) n – k .
Закон распределения для рассматриваемой случайной величины Х имеет вид:
| X
| 0
| 1
| 2
| …
| n – 1
| n
|
| P
| p 0
| p 1
| p 2
| …
| p n – 1
| p n
|
или
| X
| 0
| 1
| 2
| …
| n – 1
| n
|
| P
| (1 – p) n
| np (1 – p) n – 1
|  p 2 (1 – p) n – 2 p 2 (1 – p) n – 2
| …
| np n – 1 (1 – p)
| p n
|
Математическое ожидание M (X)= 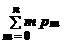 =
= 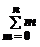
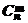 pm (1 – p) n – m = np .
pm (1 – p) n – m = np .
Дисперсия D (X) = npq .
Каждую случайную величину Х, имеющую биномиальное распределение с параметрами n и p, можно представить в виде суммы n независимых случайных величин, имеющих биномиальное распределение с параметрами n = 1 и p.
Пример 16. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равно р = 0,1. Составить закон распределения числа отказавших элементов в одном опыте, найти мат.ожидание и дисперсию данной случайной величины.
Случайная величина Х (числа отказавших элементов в одном опыте) имеет следующие возможные
значения: х 0 = 0(ни один из элементов не отказал), х 1 = 1(отказал один элемент), х 2 = 2(отказали два
элемента), х 3 = 3(отказали три элемента). Отказы элементов независимы друг от друга,
вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли.
Учитывая, что, по условию, n = 3, p = 0,1 (q = 0,9), получим: Р 3(0) = р 0 = q 3 = 0,93 = 0,729,
Р 3(1) = р 1= 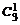 pq 2 = 3×0,1×0,92 = 0,243, Р 3(2) = р 2=
pq 2 = 3×0,1×0,92 = 0,243, Р 3(2) = р 2=  p 2 q = 3×0,12×0,9 = 0,027, Р 3(3) = р 3= p 3 = 0,13 = 0,001.
p 2 q = 3×0,12×0,9 = 0,027, Р 3(3) = р 3= p 3 = 0,13 = 0,001.
(Проверка: 0,729 + 0,243 + 0,027 + 0,001 = 1).
| Закон распределения:
| X
| 0
| 1
| 2
| 3
|
| P
| 0,729
| 0,243
| 0,027
| 0,001
|
Мат.ожидание числа отказавших элементов в одном опыте M (X) = np = 3 × 0,1 = 0,3
(проверка: 0 × 0,729 + 1 × 0,243 + 2 × 0,027 + 3 × 0,001 = 0,3). Дисперсия – npq = 3 × 0,1 × 0,9 = 0,27.
Распределение Пуассона
Дискретная случайная величина Х, которая может принимать только целые неотрицательные значения с вероятностями
p k (λ) = P (X = k) =  e –λ , k = 0, 1, …, λ > 0,
e –λ , k = 0, 1, …, λ > 0,
называется распределенной позакону Пуассона с параметром λ. В отличие от биномиального распределения, здесь случайная величина уже может принимать бесконечное число значений. Такое распределение получается в схеме Бернулли при большом числе испытаний n и малых значениях вероятности р появления события в каждом испытании (обычно достаточно выполнение условий: p < 0,1, npq < 10).
Закон распределения для рассматриваемой случайной величины Х имеет вид:
| X
| 0
| 1
| 2
| …
| n
| …
|
| P
| е –λ
| λе –λ
|  е –λ е –λ
| …
|  е –λ е –λ
| …
|
Математическое ожидание M (X)= 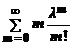 е –λ = λ .
е –λ = λ .
Дисперсия D (X)= λ .
Если независимые случайные величины Х и Y имеют распределение Пуассона с параметрами λ и μ, то их сумма Х + Y имеет распределение Пуассона с параметром λ + μ:
P (X + Y) = k) = 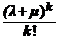 e – ( λ + μ )
e – ( λ + μ )
В вычислениях по формуле Бернулли при малых вероятностях р лучше пользоваться не приближенной формулой Лапласа (P n (k) = P k , n =  φ (x), где х =
φ (x), где х =  ), а
), а
приближенной формулой Пуассона при λ = np: P n (k) = p k , n = 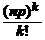 e – np .
e – np .
Пример 17. Для случайной величины Х, распределенной по закону Пуассона, вычислить Р (Х = m),
математическое ожидание и дисперсию, если λ = 0,3, m = 2.
P (X = 2) = 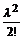 е –λ =
е –λ = 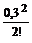 е – 0,3, M (X) = λ = 0,3, D (X) = λ = 0,3.
е – 0,3, M (X) = λ = 0,3, D (X) = λ = 0,3.
Пример 18. Проведены n независимых испытаний по схеме Бернулли. В каждом испытании может произойти событие А с вероятностью р. Подсчитать по формуле Пуассона вероятность того, что при этом событии А произошло m раз, если n = 1000, р = 0,002, m = 10.
P 1000(10)≈ P (X = 10) = 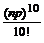 е – n p =
е – n p = 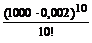 е – 2 =
е – 2 =  е – 2.
е – 2.



 pk (1 – p) n – k .
pk (1 – p) n – k . p 2 (1 – p) n – 2
p 2 (1 – p) n – 2
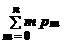 =
= 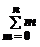
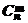 pm (1 – p) n – m = np .
pm (1 – p) n – m = np .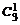 pq 2 = 3×0,1×0,92 = 0,243, Р 3(2) = р 2=
pq 2 = 3×0,1×0,92 = 0,243, Р 3(2) = р 2=  p 2 q = 3×0,12×0,9 = 0,027, Р 3(3) = р 3= p 3 = 0,13 = 0,001.
p 2 q = 3×0,12×0,9 = 0,027, Р 3(3) = р 3= p 3 = 0,13 = 0,001.  e –λ , k = 0, 1, …, λ > 0,
e –λ , k = 0, 1, …, λ > 0, е –λ
е –λ
 е –λ
е –λ
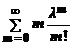 е –λ = λ .
е –λ = λ .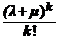 e – ( λ + μ )
e – ( λ + μ ) φ (x), где х =
φ (x), где х =  ), а
), а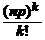 e – np .
e – np .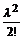 е –λ =
е –λ = 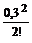 е – 0,3, M (X) = λ = 0,3, D (X) = λ = 0,3.
е – 0,3, M (X) = λ = 0,3, D (X) = λ = 0,3. 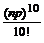 е – n p =
е – n p = 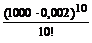 е – 2 =
е – 2 =  е – 2.
е – 2. 


