Тонкостенная труба с первоначально круговым сечением может при кручении потерять устойчивость формы и перейти в новое состояние, характеризуемое появлением продольных волн изгиба и окружных волн, превращающих круговое сечение в эллипс (n =2) или в многолепестковую фигуру (рис. 4.4.4).

Рис. 4.4.4.Форма потери устойчивости тонкостенной трубы при кручении
Кратко приведем основные соотношения для полубезмоментной теории устойчивости цилиндрической оболочки с радиусом R, толщиной стенки h и длиной L. Уравнение равновесия имеет вид
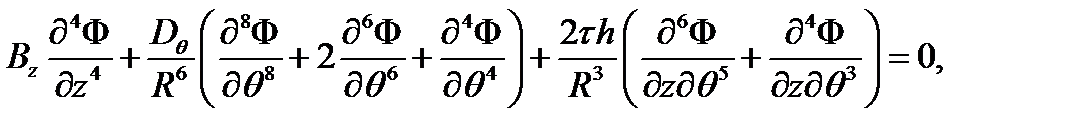
| (4.4.12)
|
где τ – распределенное касательное напряжение; Ф – функция перемещений:  осевое;
осевое; 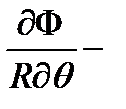 окружное;
окружное; 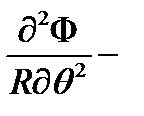 радиальноеперемещения;
радиальноеперемещения; 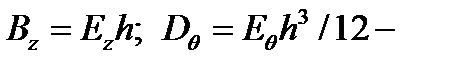 жесткости на осевое растяжение и на изгиб в окружном направлении.
жесткости на осевое растяжение и на изгиб в окружном направлении.
Для длинных оболочек можно пренебречь граничными условиями на торцах трубы и принять функцию перемещений в виде
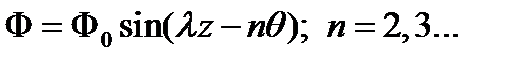
| (4.4.13)
|
Здесь n – число волн, образующихся в окружном направлении, аλ - определяет шаг спирали, по которой смещаются вершины этих волн вдоль образующей трубы. Подставив (4.4.13) в (4.4.12) и сократив на общий сомножитель 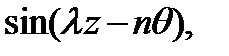 получим
получим

| (4.4.14)
|
Поскольку для длинной трубы параметр λ можно считать непрерывно меняющимся, по условию минимума требуемых для потери устойчивости напряжений 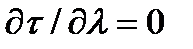 находим из (4.4.14)
находим из (4.4.14)
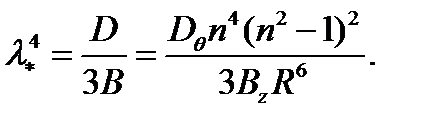
| (4.4.15)
|
Подстановка (4.4.15) в (4.4.14) даёт окончательное выражение для критического момента, минимальное значение которого соответствует n =2:

| (4.4.16)
|
Приняв как и выше приближенные зависимости модулей упругости от угла намотки волокон
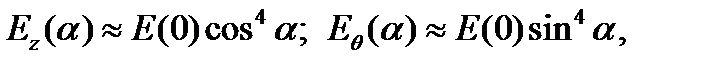
| (4.4.17)
|
найдем, что наибольший критический момент соответствует условию 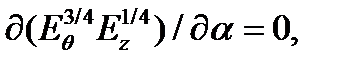 откуда
откуда 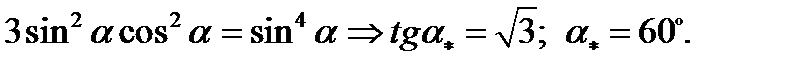
Это одно из возможных приближенных решений для длинных труб. Для удовлетворения граничным условиям на торцах трубы конечных размеров необходимо искать более сложное решение уравнения (4.4.12) в виде ряда:

Чтобы получить результат в замкнутом виде, предлагается искусственный приём: в этом ряду оставляют только два члена, разность которых обеспечивает тождественное обращение в ноль осевых перемещений на концах трубы

| (4.4.18)
|
При подстановке функции вида (4.4.18) в уравнение (4.4.12) получаем два аналогичных (4.4.14) соотношения для коэффициентов при двух разных синусах:
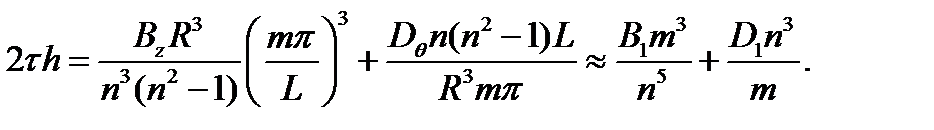
| (4.4.19)
|


Для упрощения (часто это делается молчаливо) в(4.4.19) принимается 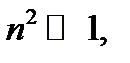 а число волн в осевом направлении считается для короткой трубы минимальным: m =1. Именно это значение соответствует из равенства двух выражений (4.4.19) наименьшему числу волн n. Тогда критическое напряжение найдется из условия
а число волн в осевом направлении считается для короткой трубы минимальным: m =1. Именно это значение соответствует из равенства двух выражений (4.4.19) наименьшему числу волн n. Тогда критическое напряжение найдется из условия 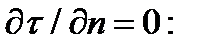
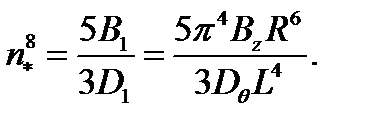
| (4.4.20)
|
Подставляя (4.4.20) в (4.4.19), получим после элементарных преобразований выражение, по размерности совпадающее с (4.4.10):

| (4.4.21)
|
Точному значению числового коэффициента 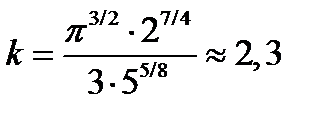 в (4.4.21) не следует придавать большой смысл, учитывая набор очень «сильных» допущений при выводе условий устойчивости. Если положить m = 2 (среднее между 1 и 3), получим
в (4.4.21) не следует придавать большой смысл, учитывая набор очень «сильных» допущений при выводе условий устойчивости. Если положить m = 2 (среднее между 1 и 3), получим 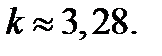 При этом из равенства двух выражений (4.4.19) для m =1 число волн
При этом из равенства двух выражений (4.4.19) для m =1 число волн  а примененное выше условие минимума
а примененное выше условие минимума 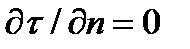 при среднем значении m = 2 даёт
при среднем значении m = 2 даёт  то есть различие в числе волн не превышает 5%. Некоторые авторы принимали другой вид решения для осевых перемещений
то есть различие в числе волн не превышает 5%. Некоторые авторы принимали другой вид решения для осевых перемещений 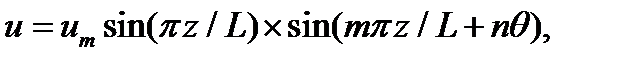 и тогда числовой коэффициент в (4.4.21) получался иным. Жесткость трубы на кручение и критический момент существенно зависят от условий закрепления торцов, но именно эти условия не удается корректносмоделировать при попытках получения аналитического решения. Применительно к вопросу выбора оптимальных углов армирования важен лишь характер зависимости критического момента(4.4.10), (4.4.21) от размеров и угла намотки трубы, позволяющий оптимизировать эти параметры по условию устойчивости формы. Само значение критического момента не может быть аналитически оценено с приемлемой достоверностью.
и тогда числовой коэффициент в (4.4.21) получался иным. Жесткость трубы на кручение и критический момент существенно зависят от условий закрепления торцов, но именно эти условия не удается корректносмоделировать при попытках получения аналитического решения. Применительно к вопросу выбора оптимальных углов армирования важен лишь характер зависимости критического момента(4.4.10), (4.4.21) от размеров и угла намотки трубы, позволяющий оптимизировать эти параметры по условию устойчивости формы. Само значение критического момента не может быть аналитически оценено с приемлемой достоверностью.
Следует отметить, что в рассмотренных схемахважную роль играет длина трубы. Если её можно принять достаточно большой (бесконечной), получается одна критическая оценка (4.4.16); если труба короткая, то справедлива другая предельная формула (4.4.21), но обе эти формулы – приближенные. В заключение заметим, что потеря формы при кручении возникает лишь для весьма тонкостенных труб («консервная банка»), и её легко можно избежать, повышая толщину стенки или выбирая соответствующие углы армирования.
Баллон для сжатого газа.
Цель данного и двух предыдущих параграфов 4.4.1 и 4.4.2 -показать на простейших примерах композитной цилиндрической трубы, как разные требования приводят к различным оптимальным углам намотки: для баллона – это + 540, для быстровращающегося вала – это 0, для торсиона – + 450. Отметим, что для металлов задача подбора структуры материала под вид напряженного состояния вообще не может быть поставлена, однако живая Природа всегда оптимизирует структуру армирования по только Ей известным законам, которые мы пытаемся понять.




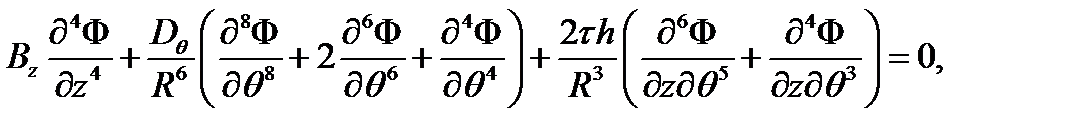
 осевое;
осевое; 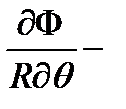 окружное;
окружное; 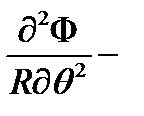 радиальноеперемещения;
радиальноеперемещения; 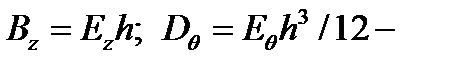 жесткости на осевое растяжение и на изгиб в окружном направлении.
жесткости на осевое растяжение и на изгиб в окружном направлении.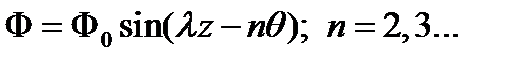
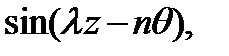 получим
получим
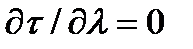 находим из (4.4.14)
находим из (4.4.14)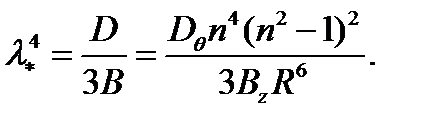

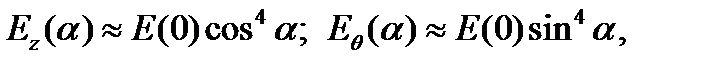
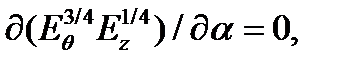 откуда
откуда 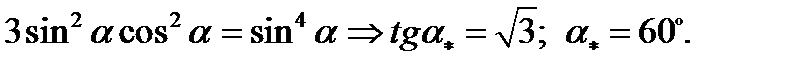


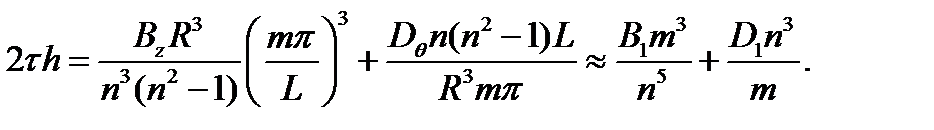


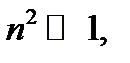 а число волн в осевом направлении считается для короткой трубы минимальным: m =1. Именно это значение соответствует из равенства двух выражений (4.4.19) наименьшему числу волн n. Тогда критическое напряжение найдется из условия
а число волн в осевом направлении считается для короткой трубы минимальным: m =1. Именно это значение соответствует из равенства двух выражений (4.4.19) наименьшему числу волн n. Тогда критическое напряжение найдется из условия 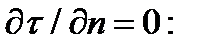
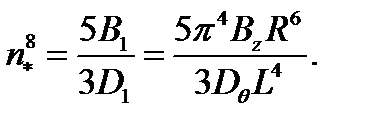

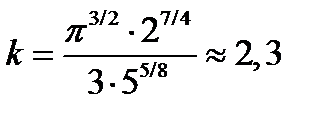 в (4.4.21) не следует придавать большой смысл, учитывая набор очень «сильных» допущений при выводе условий устойчивости. Если положить m = 2 (среднее между 1 и 3), получим
в (4.4.21) не следует придавать большой смысл, учитывая набор очень «сильных» допущений при выводе условий устойчивости. Если положить m = 2 (среднее между 1 и 3), получим 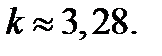 При этом из равенства двух выражений (4.4.19) для m =1 число волн
При этом из равенства двух выражений (4.4.19) для m =1 число волн  а примененное выше условие минимума
а примененное выше условие минимума 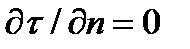 при среднем значении m = 2 даёт
при среднем значении m = 2 даёт  то есть различие в числе волн не превышает 5%. Некоторые авторы принимали другой вид решения для осевых перемещений
то есть различие в числе волн не превышает 5%. Некоторые авторы принимали другой вид решения для осевых перемещений 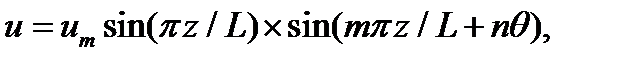 и тогда числовой коэффициент в (4.4.21) получался иным. Жесткость трубы на кручение и критический момент существенно зависят от условий закрепления торцов, но именно эти условия не удается корректносмоделировать при попытках получения аналитического решения. Применительно к вопросу выбора оптимальных углов армирования важен лишь характер зависимости критического момента(4.4.10), (4.4.21) от размеров и угла намотки трубы, позволяющий оптимизировать эти параметры по условию устойчивости формы. Само значение критического момента не может быть аналитически оценено с приемлемой достоверностью.
и тогда числовой коэффициент в (4.4.21) получался иным. Жесткость трубы на кручение и критический момент существенно зависят от условий закрепления торцов, но именно эти условия не удается корректносмоделировать при попытках получения аналитического решения. Применительно к вопросу выбора оптимальных углов армирования важен лишь характер зависимости критического момента(4.4.10), (4.4.21) от размеров и угла намотки трубы, позволяющий оптимизировать эти параметры по условию устойчивости формы. Само значение критического момента не может быть аналитически оценено с приемлемой достоверностью.

