Порядок расчета статически неопределимых систем методом сил

Расчет статически неопределимой системы начинается с анализа ее схемы. Анализ необходим прежде всего для того, чтобы установить степень статической неопределимости.

Степень статической неопределимости равна числу так называемых лишних связей, удаление которых превращает статически неопределимую систему в определимую геометрически неизменяемую систему.

Геометрически неизменяемой называется такая система, изменение формы которой возможно лишь в связи с деформациями ее элементов.

Статически определимая система не имеет ни одной лишней связи; удаление из нее хотя бы одной связи превращает ее в геометрически изменяемую систему, т.е. в механизм.

Необходимо заметить, что исключение лишних связей для превращения одной и той же статически неопределимой конструкции в статически определимую может быть произведено различными способами, однако число отбрасываемых связей всегда будет одно и то же.

На первом этапе расчета необходимо от заданной статически неопределимой рамы перейти к «основной» системе. Для этого необходимо отбросить «лишние связи» и приложить неизвестные усилия по их направлению.

На втором этапе расчета необходимо записать канонические уравнения метода сил. Количество уравнений будет соответствовать количеству неизвестных усилий.  Если неизвестное усилие одно, то будем иметь одно каноническое уравнение; если несколько – то систему канонических уравнений.

Для того, чтобы решить систему канонических уравнений, т.е. найти неизвестные Х₁, Х₂ и т.д., необходимо определить коэффициенты канонических уравнений. Эти коэффициенты вычисляются путем использования правила Верещагина (перемножения эпюр). Для этого выполняют построение грузовой эпюры и единичных эпюр изгибающих моментов. Количество единичных эпюр моментов соответствует числу неизвестных. Все эти эпюры строятся в «основной системе».

Определив коэффициенты, производят их подстановку в систему канонических уравнений. Результатом решения системы будут являться истинные значения Х₁, Х₂ и т.д., которые будем рассматривать как множители к единичным эпюрам для получения «исправленных» эпюр.

Окончательная эпюра изгибающих моментов получается путем сложения «исправленных» эпюр и грузовой эпюры моментов.

На этом этапе необходимо провести промежуточную проверку равновесия узлов. Вырезав внутренние жесткие узлы, прикладываем моменты, взятые с окончательной эпюры М, соблюдая правило знаков. Находим алгебраическую сумму моментов и убеждаемся в нулевом результате.

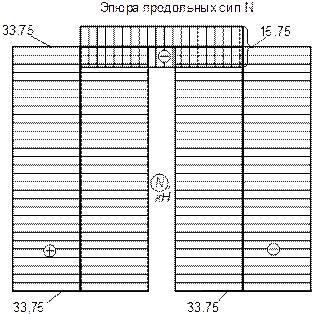
Используя окончательную эпюру моментов, выполняем построение эпюры поперечных сил Q. Рассматривая равновесие узлов при использовании ординат эпюры Q, вычисляем продольные усилия в стержнях рамы и на основании этого ведем построение эпюры продольных сил N.

На последнем этапе расчета производим общую проверку равновесия рамы. Для этого к исходной раме прикладываем заданную нагрузку. На этой же раме показываем все опорные реакции, взяв всю необходимую информацию для этого из окончательной эпюры М, Q и N. Составляем три уравнения равновесия (сумма проекций всех сил на ось Х; сумма проекций всех сил на ось Y; сумма моментов всех сил относительно произвольной точки). После необходимой подстановки нулевой результат указывает на равновесие рамы и, соответственно, правильность решения.

 

 

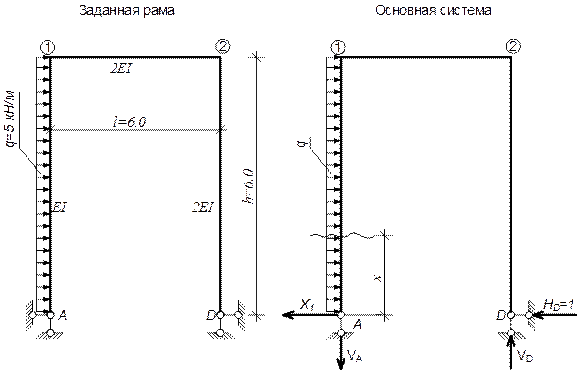
Пример 1. Построить эпюры Q , М и N для рамы. Жесткости элементов рамы указаны на рисунке.

1. Выявляем степень статической неопределимости.

Л=3К - Ш = 3 -1 —2 = 1 (или Л = С_оп —3 = 4 —3= 1 ).

2. Выбираем основную систему и обращаем ее в нагруженную систему. Основ­ную систему получаем из заданной, устраняя нагрузку и горизонтальный опорный стержень левой опоры. Основная система, нагруженная заданной нагрузкой и горизонтальной неизвестной Х₁ возмещающей действие на раму устраненной связи.

3. Составляем каноническое уравнение:

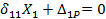
Это уравнение в данном случае выражает условие равенства нулю горизонталь­ного перемещения точки А в системе совместного действия неиз­вестной Х₁ и заданной нагрузки.

4. Вычисляем перемещения 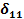 и 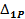 ; для этого предварительно строим эпюры и M_P .

а) Эпюра :

Нагрузим для этого основную систему только силой 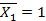 . Вертикальные опорные реакции от данного нагружения равны нулю (к та­кому заключению легко прийти, если составить уравнения

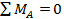   и 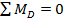. Горизонтальную реакцию найдем из уравнения :

, откуда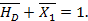

 

Изгибающие моменты в характерных сечениях элементов.

Элемент А1: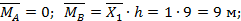

Элемент 12: ;  

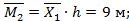
Элемент CD: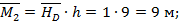

Б) Эпюра М _P

Нагрузив основную систему заданной нагрузкой, найдем сначала опорные реакции:

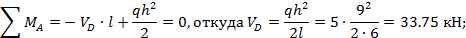
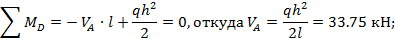
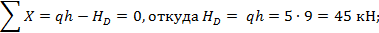
Теперь вычислим значения изгибающих моментов, необходимые для построе­ния эпюры М _P; эти же значения в дальнейшем используем при построении окон­чательной эпюры М:

Элемент A2: Здесь 0≤х ≤9м и 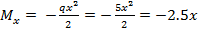 - уравнение квадратной параболы;

при х=0: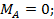

при x = 4,5 м: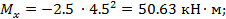

при х = 9м:

Элемент 1-2:

 

 

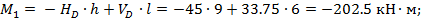
Элемент 2- D:

   

 

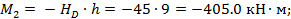
По данным построенных эпюр и М _P находим:

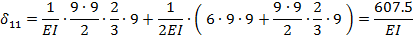
Для получения 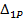 умножим площади ω, взятые из эпюры М _P на ординаты у, взятые из эпюры :

 

 

 

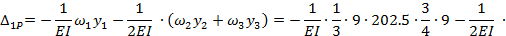
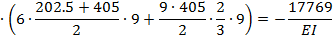
5. Находим из канонического уравнения значение Х₁:

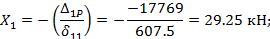
Знак плюс свидетельствует о правильности принятого направления найденной нами лишней неизвестной Х₁.

6. Строим окончательные эпюры Q, М и N.

 

а) Эпюра Q.

Вычислим опорные реакции, нагрузив основную систему заданной нагрузкой и известной теперь силой Х₁. Ввиду того что силы Х₁ и Н _D дей­ствуют по одной прямой, проходящей через центры опорных шарниров, относи­тельно которых следует составить уравнения моментов для определения реакций V_А и V _D и моментов относительно этих точек не дают, вертикальные опорные реак­ции в данном случае будут такими же, как и соответствующие реакции, вычис­ленные для построения эпюры М _P, т. е.

V_A = 33,75 кН; V_D = 33,75 кН.

Реакцию H_D найдем из уравнения ∑Х = 0:

—X₁ + qh — H_D = 0, откуда H_D = —X₁ + qh = — 29,25+5 · 9= 15,75 кН.

Вычисляем поперечные силы в характерных сечениях.

Элемент А1: 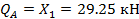 м;

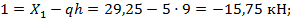
Элемент 1-2: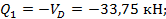  

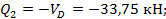
Элементн 2 D: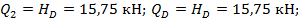  

 

б) Эпюра М.

Произведем для характерных сечений сложение ординат эпюры М_P с соответ­ствующими ординатами эпюры  увеличенными в Х₁ = 29,25 раз.

Элемент А1: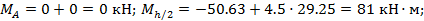  

 

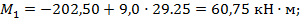
Найдем расстояние х₀ до сечения с максимальным изгибающим моментом, приравняв нулю поперечную силу в этом сечении:

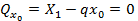, откуда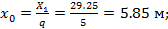

Тогда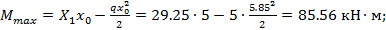

Элемент 1-2: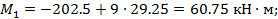  

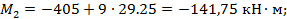
Элемент 2- D: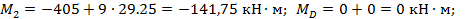  

 

в) Эпюра N.

Вычислим продольные силы в элементах рамы:

Элемент A1. Во всех сечениях рассматриваемого элемента продольная сила имеет постоянное значение: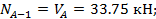

Элемент 1-2: В данном элементе продольная сила также постоянна:

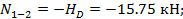
Элемент 2- D. И в данном элементе продольная сила постоянна:

 

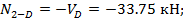
Пример 2. Построить эпюры Q , М и N для рамы. Жесткости элементов указаны на рисунке.

1. Устанавливаем степень статической неопределимости:

Л= 3К – Ш= 3·1 – 1=2 (или Л= С_оп -2=5-3 = 2) - рама дважды статически неопределима.

2. Выбираем основную систему и обращаем ее в нагруженную. Устранив заданную нагрузку, а также горизонтальный и вертикальный опорные стержни левой опоры (всю опору А), получим основную систему в виде ломаного бруса с одним свободным, другим защемленным концами. Основная система, нагружен­ная заданной нагрузкой и лишними неизвестными X₁ и Х₂, заменяющими соответ­ственно устраненные горизонтальный и вертикальный стержни опоры А.

3. Составляем канонические уравнения.

В данном случае будем иметь два канонических уравнения, что соответствует двум лишним неизвестным:

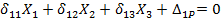
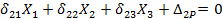
Первое из этих уравнений выражает условие равенства нулю горизонтального перемещения точки А в системе от совместного действия сил X₁ , Х₂ и заданной нагрузки, второе — условие равенства нулю вертикального перемеще­ния точки А от тех же сил.

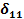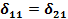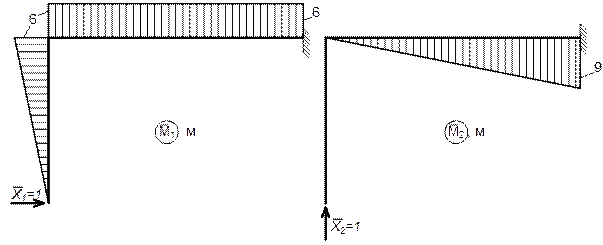
4. Вычисляем перемещения , , , 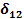∆_1Р и ∆_2Р; для этого предвари­тельно строим эпюры и 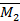 от поочередного нагружения основной системы соот­ветственно силами ,

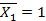 и эпюру М _P от нагружения основной системы заданной нагрузкой. Ввиду простоты построения указанных эпюр соответствую­щие вычисления здесь не приводим. Отметим только, что при определении момента в том или ином сечении следует рассматривать левую отсеченную часть рамы; в зтом случае не потребуется определять опорные реакции в заделке. Эпюры  , , 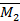 и М _P показаны.

Теперь вычисляем перемещения, входящие в составленные выше каноничес­кие уравнения:

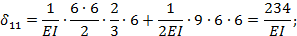
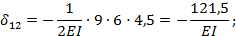
где 9·6 — площадь прямоугольной части эпюры  ; 4,5 — ордината, соответ­ствующая центру тяжести этой площади и взятая из эпюры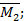

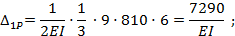
где 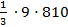 — площадь параболической части эпюры М _P; 6—ордината из эпюры  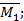соответствующая центру тяжести указанной площади;

 

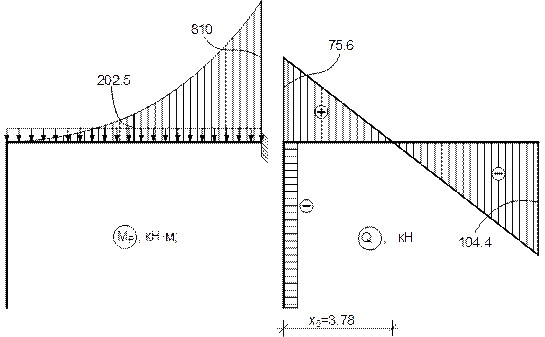
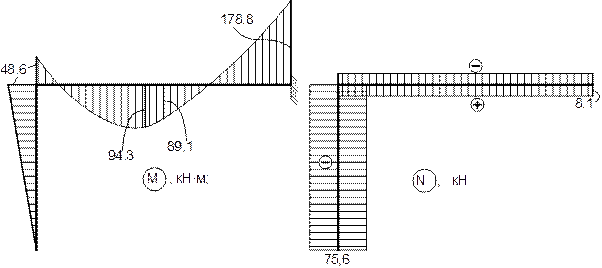
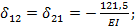 (на основании теоремы Максвелла);

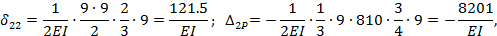
где 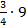 — ордината из зпюры 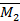, соответствующая центру тяжести площади пара­болической части эпюры М _P.

5. Подставляем найденные значения перемещений в канонические уравнения и решаем полученную систему уравнений:

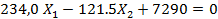
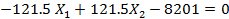
откуда 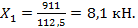Подставив найденное значение Х₁ в любое из уравнений, получим

Х₂ =75,6 кН.

Положительные значения Х₁ и Х₂ свидетельствуют о правильности выбора направлений обоих лишних неизвестных.

Проверим правильность решения системы канонических уравнений, подста­вив в каждое из них найденные значения Х₁ и Х₂:

234·8,1 — 121,5·75,6 + 7290 = 9185,4 — 9185,4 = 0;

— 121,5·8,1 + 121,5·75,6 — 8201 = — 9185,15 + 9185,4 = 0,25.

Погрешность во втором уравнении составляет всего (0,25/9185,15) 100 = 0,0027 %, поэтому практически в этом уравнении результат можно принять также равным нулю. Итак, система канонических уравнений решена правильно.

 

6. Строим окончательные эпюры Q, М и N.

а) Эпюра Q.

Вычислим значения поперечных сил для характерных сечений:

Элемент А-1: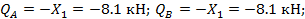

Элемент 1-С: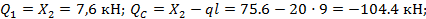

 

б) Суммарная (окончательная) эпюра М.

Сложим для характерных сечений системы ординаты эпюры М _P с соответствующими ординатами эпюры  умноженными на Х₁ = 8,1 кН, и ор­динатами эпюры 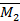, умноженными на Х₂ = 75,6 кН.

Элемент А-1: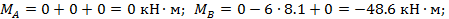

Элемент 1- C: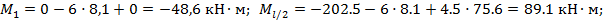

 

Найдем расстояние до сечения с максимальным изгибающим моментом, со­ставив выражение поперечной силы в этом сечении и приравняв его нулю:

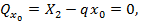 откуда

Тогда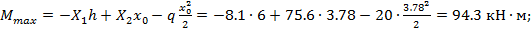

в) Эпюра N.

В каждом из элементов рамы продольная сила имеет свое постоянное значе­ние:

 

 

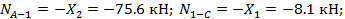
Пример 3. Построить эпюры Q , М и N для рамы. Жесткости элементов указаны на рисунке.

 

 

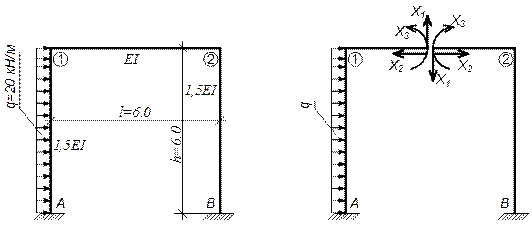
1. Рама трижды статически неопределима, так как

Л = 3К -Ш = 3 ∙ 1—0 = 3 (или Л = С_0П - 3 = 6 - 3 = 3).

 

2. Для упрощения расчета используем симметрию заданной системы.

3. Составим канонические уравнения, которые в порядке написания будут выражать условия равенства нулю: вертикального взаимного сдвига смежных сечений в месте разреза, взаимного горизонтального смещения этих сечений и их взаимного угла поворота:

 

КАНОНИЧЕСКИЕ УРАВНЕНИЯ

 

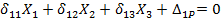
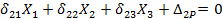
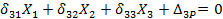
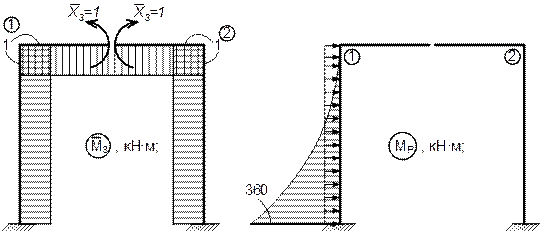
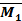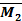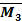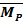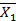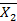4. Далее построим эпюры , ,  и  от поочередного раздельного нагружения основной системы силами = 1, = 1, 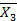= 1 и заданной нагруз­кой.

Сопоставляя построенные эпюры, приходим к заключению, что эпюры  и 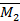, а также эпюры  и 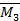 взаимно ортогональны по свойству прямой и обратной симметрии. Следовательно,

Теперь канонические уравнения можно представить в более упрощенном виде:

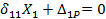
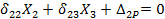
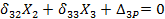
Как видим, система трех уравнений с тремя неизвестными распалась на две независимые, системы: одно уравнение с одним неизвестным Х₁ и два уравнения с двумя неизвестными Х₂ и Х₃.

Следует иметь в виду, что выбор основной системы путем разреза симметрич- ной заданной системы по оси симметрии и введения в месте разреза симметричных и обратно симметричных лишних неизвестных всегда позволяет привести общую систему канонических уравнений к двум независимым системам, одна из которых содержит только симметричные, другая — только обратно симметричные лишние неизвестные.

Вычислим входящие в полученные уравнения перемещения 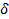 и :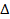

 

 

 

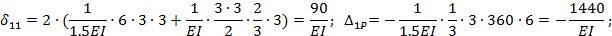
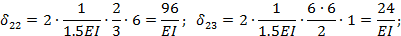
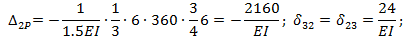
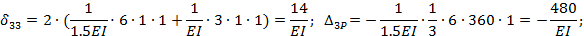
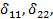
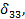
Обращаем внимание, что при определении перемещений 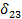сразу же после первого знака равенства поставлен коэффициент 2. Это значит, что перемножение соответствующих эпюр ведется для левой (или правой) части основ­ной системы и результат удваивается.