Я. Л. Либерман проф., М. С. Антропов
(Уральский федеральный университет имени первого Президента России Б.Н.Ельцина, г. Екатеринбург)
mikhaill88@mail.ru
Предложена система управления скоростью робокара с элементами искусственного интеллекта, построенная на основе математического аппарата нечёткой логики (фаззи-логики). Система позволяет автоматически изменять скорость движения робокара в зависимости от массы перемещаемого груза и радиуса закругления пути. Описан алгоритм работы системы и его программная реализация на языке Delphi, а также оригинальная схема преобразователя радиуса поворота робокара в код. Робокар с рассмотренной системой управления скоростью может быть применён в гибких автоматизированных цехах и участках.
Proposed a system of speed control robocars with artificial intelligence elements constructed on the basis of the mathematical apparatus of fuzzy logic. The system allows you to change the speed of the robocar according to the mass of transported goods and the radius of curvature of the path. The algorithm of the system and its implementation in the language of Delphi, as well as the original scheme of the converter turning radius robocar code. robocar with a speed control system under consideration can be applied in flexible automation workshops and locations.
Ключевые слова: робот, гибкое производство, управление.
Keywords: robot, flexible production, management.
В гибких производственных системах (ГПС) зачастую используются безрельсовые робокары, траектория движения которых задается управляющей микро-ЭВМ, работающей совместно с устройством маршрутослежения оптоэлектронного (излучатель – светоотражающая полоса) или индуктивного типа (пара индуктивных датчиков, включённых по дифференциальной схеме, – низкочастотный кабель) [1, 2]. Таковы, в частности, робокары на базе автоматических тележек типа «Электроника», МП-12Т, а также тележки, разработанной в Институте атомной энергетики им. И.В.Курчатова и др. [3]. Движение подобных робокаров, как правило, происходит с постоянной скоростью, обеспечивающей безопасность транспортирования грузов. Вместе с тем, движение с постоянной скоростью не всегда позволяет минимизировать время доставки грузов по назначению и обеспечить требуемую производительность робокара. С этой точки зрения представляется целесообразной разработка системы управления скоростью робокара, дополняющей систему управления траекторией его движения. Такая система, разработанная в УрФУ, и описывается в настоящей статье. Построена она применительно к робокару со следующими техническими характеристиками: максимальная масса транспортируемого груза – 500 кг, габаритные размеры робокара – 1800х850 мм, расстояние между осями колес – 100 см.
В связи с трудностью расчета сил сцепления колес робокара с поверхностью пола цеха при различных нагрузках и определения центробежных сил, действующих на робокар на поворотах, по-видимому, имеет смысл обратиться к опыту квалифицированных водителей электрокаров и строить нужную систему управления скоростью, используя указанный опыт. Осуществить это можно, применяя элементы искусственного интеллекта, базирующиеся на математическом аппарате нечёткой логики или фаззи-логики.
Главным звеном всякой системы управления, базирующейся на фаззи-логике, является фаззи-регулятор, действие которого основано на знаниях экспертов, способных сформулировать базу правил в форме [4]
ЕСЛИ (предпосылка), ТО (вывод).
На этих знаниях строится база данных с функциями принадлежности для предпосылок (входных переменных) и выводов (выходной переменной). В рассматриваемом случае функциями принадлежности для предпосылок могут быть f(m) и f(R), а для выводов – f(v), где m – масса груза, перевозимого робокаром, R – текущий радиус поворота, v – текущая скорость робокара).
Функция принадлежности, в общем случае, – это функция, показывающая, в какой степени (насколько) элементы некоторого множества обладают характеристическим свойством, используемым для задания этого множества [5]. Одной из самых простых является треугольная функция принадлежности вида
f(x,a,b) = |x-a|/b, (1)
где x – переменная, a и b – параметры. Функция обладает достаточной адаптационной способностью, а потому в качестве f(m), f(R) и f(v) при разработке требуемой системы управления приняли именно её.
Для конкретизации параметров кривой (1) применительно к лингвистическим переменным m, R, v и их интервалам, обозначенным, как это принято в нечёткой логике, символическими именами – термами, вначале потребовалось описать знания экспертов в виде эвристических постулатов:
движение по прямой, то есть радиус очень-очень большой (ОЧ ОЧ Б), следует производить с максимальной (М) скоростью, независимо от массы груза;
если масса очень малая (ОЧ М) и радиус очень малый (ОЧ М), то робокар должен двигаться с малой рабочей (МР) скоростью;
если масса очень малая (ОЧ М) и радиус малый (МАЛ), то робокар должен двигаться со средней рабочей (СР) скоростью;
если масса очень малая (ОЧ М) и радиус средний (СР), то робокар должен двигаться с большой рабочей (БР) скоростью;
если масса очень малая (ОЧ М) и радиус большой (БОЛ), то робокар должен двигаться с наибольшей рабочей (НБР) скоростью;
если масса очень малая (ОЧ М) и радиус очень большой (ОЧ Б), то робокар должен двигаться с максимальной (М) скоростью;
если масса малая (МАЛ) и радиус очень малый (ОЧ М), то робокар должен двигаться с малой рабочей (МР) скоростью;
если масса малая (МАЛ) и радиус малый (МАЛ), то робокар должен двигаться со средней рабочей (СР) скоростью;
если масса малая (МАЛ) и радиус средний (СР), то робокар должен двигаться со средней рабочей (СР) скоростью;
если масса малая (МАЛ) и радиус большой (БОЛ), то робокар должен двигаться с большой рабочей (БР) скоростью;
если масса малая (МАЛ) и радиус очень большой (ОЧ Б), то робокар должен двигаться с наибольшей рабочей (НБР) скоростью;
если масса средняя (СР) и радиус очень малый (ОЧ М), то робокар должен двигаться с наименьшая рабочей (НМР) скоростью;
если масса средняя (СР) и радиус малый (МАЛ), то робокар должен двигаться с малой рабочей (МР) скоростью;
если масса средняя (СР) и радиус средний (СР), то робокар должен двигаться со средней рабочей (СР) скоростью;
если масса средняя (СР) и радиус большой (БОЛ), то робокар должен двигаться с большой рабочей (БР) скоростью;
если масса средняя (СР) и радиус очень большой (ОЧ Б), то робокар должен двигаться с наибольшая рабочей (НБР) скоростью;
если масса большая (БОЛ) и радиус очень малый (ОЧ М), то робокар должен двигаться с ползучей (П) скоростью;
если масса большая (БОЛ) и радиус малый (МАЛ), то робокар должен двигаться с наименьшей рабочей (НМР) скоростью;
если масса большая (БОЛ) и радиус средний (СР), то робокар должен двигаться с малой рабочей (МР) скоростью;
если масса большая (БОЛ) и радиус большой (БОЛ), то робокар должен двигаться со средней рабочей (СР) скоростью;
если масса большая (БОЛ) и радиус очень большой (ОЧ Б), то робокар должен двигаться с большой рабочей (БР) скоростью;
если масса очень большая (ОЧ Б) и радиус очень малый (ОЧ М), то робокар должен двигаться с ползучей (П) скоростью;
если масса очень большая (ОЧ Б) и радиус малый (МАЛ), то робокар должен двигаться с ползучей (П) скоростью;
если масса очень большая (ОЧ Б) и радиус средний (СР), то робокар должен двигаться с наименьшей рабочей (НМР) скоростью;
если масса очень большая (ОЧ Б) и радиус большой (БОЛ), то робокар должен двигаться с малой рабочей (МР) скоростью;
если масса очень большая (ОЧ Б) и радиус очень большой (ОЧ Б), то робокар должен двигаться со средней рабочей (СР) скоростью.
Максимальное значение всякой функции принадлежности, по определению, равно 1. Согласно работе [4], правомерно полагать, что значения функций, соответствующих двум соседним термам, в точке их пересечения равны 0,5. Учитывая это и исходя из типичных условий эксплуатации робокаров, далее были получены интерпретации функции принадлежности типа треугольной для пяти термов лингвистической переменной m, шести термов лингвистической переменной R и семи термов лингвистической переменной v (табл. 1, рис.1). Это позволило организовать сформулированные правила в виде матрицы (табл. 2). С
Интерпретации функции принадлежности (1)
| Лингвисти-ческая переменная
| Обозна-чение терма
| Интервал, соответст-вующий терму
| Функция принадлежности, соответствующая терму
|
| m
| ОЧ М
| [0 ; 50]
| f 1(m) = 1
|
| [50 ; 150]
| f 1(m) = (150 – m)/100
|
| МАЛ
| [50 ; 150]
| f 2(m) = (m – 50)/100
|
| [150 ; 250]
| f 2(m) = (250 – m)/100
|
| СР
| [150 ; 250]
| f 3(m) = (m – 150)/100
|
| [250 ; 350]
| f 3(m) = (350 – m)/100
|
| БОЛ
| [250 ; 350]
| f 4(m) = (m – 250)/100
|
| [350 ; 450]
| f 4(m) = (450 – m)/100
|
| ОЧ Б
| [350 ; 450]
| f 5(m) = (m – 350)/100
|
| [450 ; 500]
| f 5(m) = 1
|
| R
| ОЧ М
| [140 ; 156]
| f 1(R) = (156 – R)/16
|
| МАЛ
| [140 ; 156]
| f 2(R) = (R – 140)/16
|
| [156 ; 175]
| f 2(R) = (175 – R)/19
|
| СР
| [156 ; 175]
| f 3(R) = (R – 156)/19
|
| [175 ; 200]
| f 3(R) = (200 – R)/25
|
| БОЛ
| [175 ; 200]
| f 4(R) = (R – 175)/25
|
| [200 ; 240]
| f 4(R) = (240 – R)/40
|
| ОЧ Б
| [200 ; 240]
| f 5(R) = (R – 200)/40
|
| ОЧ ОЧ Б
| > 240
| f 6(R) = 1
|
| v
| П
| [0,1 ; 0,2]
| f 1(v) = (0,2 – v)/0,1
|
| НМР
| [0,1 ; 0,2]
| f 2(v) = (v – 0,1)/0,1
|
| [0,2 ; 0,3]
| f 2(v) = (0,3 – v)/0,1
|
| МР
| [0,2 ; 0,3]
| f 3(v) = (v – 0,2)/0,1
|
| [0,3 ; 0,4]
| f 3(v) = (0,4 – v)/0,1
|
| СР
| [0,3 ; 0,4]
| f 4(v) = (v – 0,3)/0,1
|
| [0,4 ; 0,5]
| f 4(v) = (0,5 – v)/0,1
|
| БР
| [0,4 ; 0,5]
| f 5(v) = (v – 0,4)/0,1
|
| [0,5 ; 0,6]
| f 5(v) = (0,6 – v)/0,1
|
| НБР
| [0,5 ; 0,6]
| f 6(v) = (v – 0,5)/0,1
|
| [0,6 ; 0,7]
| f 6(v) = (0,7 – v)/0,1
|
| М
| [0,6 ; 0,7]
| f 7(v) = (v – 0,6)/0,1
|
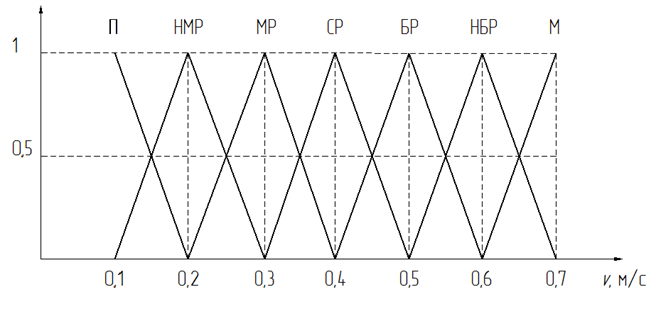
 Рис. 1. Графики функций принадлежности:
Рис. 1. Графики функций принадлежности:
а – для лингвистической переменной m, б – для лингвистической переменной R, в – для лингвистической переменной v.
 Матрица правил
Матрица правил
| Радиус
| Масса
|
| ОЧ М
| МАЛ
| СР
| БОЛ
| ОЧ Б
|
| ОЧ М
| МР
| МР
| НМР
| П
| П
|
| МАЛ
| СР
| СР
| МР
| НМР
| П
|
| СР
| БР
| СР
| СР
| МР
| НМР
|
| БОЛ
| НБР
| БР
| БР
| СР
| МР
|
| ОЧ Б
| М
| НБР
| НБР
| БР
| СР
|
| ОЧ ОЧ Б
| М
| М
| М
| М
| М
|
помощью этой матрицы нетрудно производить операцию фаззификации – установление соответствия между конкретным значением отдельной входной переменной и значением функции принадлежности соответствующего ей терма переменной. Поскольку нечёткая логика предполагает возможность частичного наложения термов, в процессе фаззификации не исключено получение нескольких значений функции принадлежности, соответствующих одному значению лингвистической переменной. Для того чтобы остановиться на одном из полученных значений, после фаззификации обычно производят агрегирование. Эта операция представляет собой процедуру определения степени истинности найденных значений функций принадлежности и установление связи между ними, описываемой, чаще всего, либо логическим «и», либо логическим «или». В данном случае указанная связь описана как «и».
После агрегирования фаззи-регулятор должен выполнять активирование – операцию, направленную на расширение агрегирования на все правила, описанные матрицей. Эта операция аналогична композиции нечётких отношений и в рассматриваемом случае была выполнена простейшим образом – по условию минимума. Это дало возможность далее достаточно легко (по правилу максимума) осуществить операцию аккумулирования – процедуру отыскания значения функции принадлежности входного параметра регулятора.
Операции агрегирования, активирования и аккумулирования в совокупности представляют собой механизм нечётких выводов, в результате которых переменной m присваивается значение входной переменной m', переменной R присваивается значение входной переменной R ', и обусловленные этим f(m)=f(m') и f(R)=f(R ') дают вполне определённую функцию f(m', R ',v). Если теперь произвести операцию дефаззификации – отыскание по f(m', R ',v) величины v' (удобнее всего для этого применить метод центра тяжести), то нетрудно получить значение требуемой скорости движения робокара, отвечающее исходной базе знаний.
Построенный на основе описанных принципов фаззи-регулятор формирует выходной сигнал, задающий скорость движения робототележки в процессе её движения.
Функциональная схема предлагаемой системы управления (рис. 2) включает в себя датчики массы и радиуса поворота робокара, аналого-цифровой преобразователь, преобразователь код-код, фаззи-регулятор, цифро-аналоговый преобразователь и регулируемый привод перемещения.
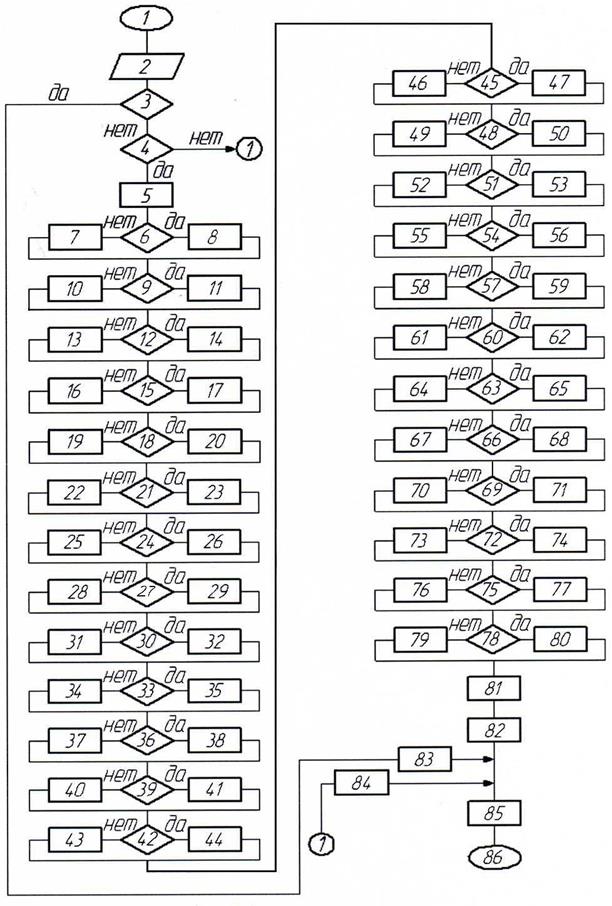
Алгоритм работы фаззи-регулятора представлен на рис. 3, где 1 – начало; 2 – ввод массы груза и радиуса поворота робокара; 3 – проверка: R' >240?; 4 – проверка: значения массы груза и радиуса принадлежат заданному интервалу?; 5 – фаззификация входных переменных (массы груза и радиуса); 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78 – проверка: f i(m')>0 И f j(R')>0 И f i(m')>f j(R')?; 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58, 61, 64, 67, 70, 73, 76, 79 – присвоение переменной f(m, R', v) значения f j(R'); 8, 11, 14, 17, 20, 23, 26, 29, 32, 35, 38, 41, 44, 47, 50, 53, 56, 59, 62, 65, 68, 71, 74, 77, 80 – присвоение переменной f(m', R, v) значения f i(m'); 81 – аккумулирование (выбор наибольшего значения) функций принадлежности f(m', R', v); 82 – деффазификация выходной переменной скорости v' по формуле
v' = [f1(v)· v1+ f 2(v)· v 2+ f 3(v)· v 3+ f 4(v)· v 4+ f 5(v)· v 5+ f 6(v)· v 6+ f 7(v)· v 7]/ /[f1(v)+f 2(v)+f3(v)+f4(v)+f5(v)+f6(v)+f7(v)];
83 – присвоение величине v' значения 0,7 при R'>240; 84 – присвоение величине v' значения 0 при ошибке ввода; 85 – вывод значения v'; 86 – конец.
Принцип действия и устройство датчика радиуса поворота робокара могут быть проиллюстрированы рис. 4 и 5. Этот датчик служит для преобразования угла поворота β руля тележки робокара непосредственно в естественный двоичный код (ЕДК) радиуса R. Для этого он снабжён кодовой шкалой, на которую в соответствии с комбинациями ЕДК, отображающими R, нанесены активные и пассивные (в частности, магнитные и немагнитные) участки, и системой считывания кода со шкалы (в частности, магнитными головками). Шкала построена по таблице соответствий β и R (табл. 3) и имеет тринадцать основных дорожек по числу разрядов двоичных эквивалентов R. Она закрепляется неподвижно на корпусе робототележки, а система считывания – также неподвижно, но на руле. При повороте руля относительно корпуса, головки считывают кодовые комбинации со шкалы и водят их в фаззи-

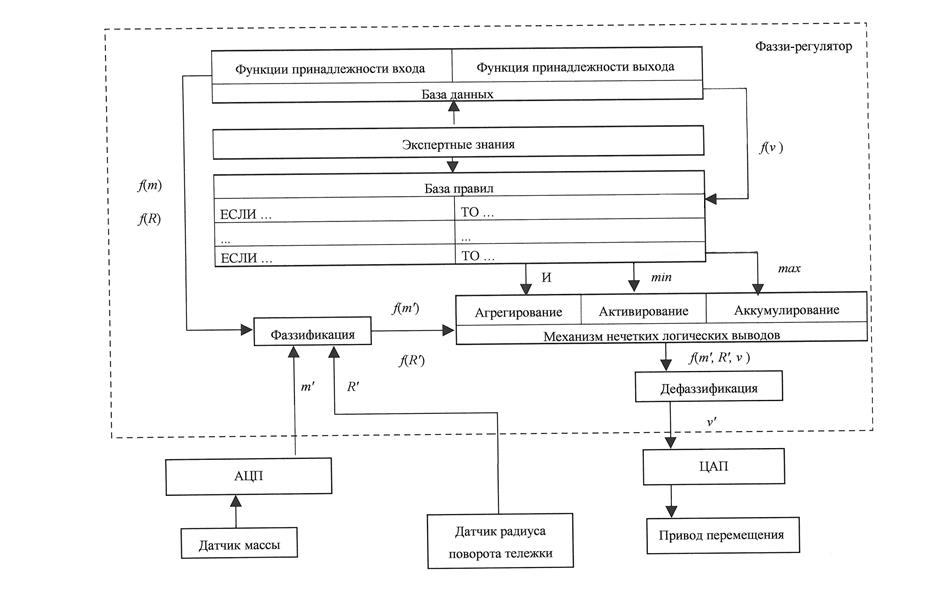
Рис.3. Алгоритм работы фаззи-регулятора
Таблица соответствий
| угол
β, град
| Радиус R,
см
| ЕДК радиуса
R
| угол
β, град
| Радиус R,
см
| ЕДК радиуса
R
|
| 45
| 141
| 0 000 010 001 101
| 22
| 267
| 0 000 100 001 011
|
| 44
| 144
| 0 000 010 010 000
| 21
| 279
| 0 000 100 010 111
|
| 43
| 147
| 0 000 010 010 011
| 20
| 292
| 0 000 100 100 100
|
| 42
| 149
| 0 000 010 010 101
| 19
| 307
| 0 000 100 110 011
|
| 41
| 152
| 0 000 010 011 000
| 18
| 324
| 0 000 101 000 100
|
| 40
| 156
| 0 000 010 011 100
| 17
| 342
| 0 000 101 010 110
|
| 39
| 159
| 0 000 010 011 111
| 16
| 363
| 0 000 101 101 011
|
| 38
| 162
| 0 000 010 100 010
| 15
| 386
| 0 000 110 000 010
|
| 37
| 166
| 0 000 010 100 110
| 14
| 413
| 0 000 110 011 101
|
| 36
| 170
| 0 000 010 101 010
| 13
| 445
| 0 000 110 111 101
|
| 35
| 174
| 0 000 010 101 110
| 12
| 481
| 0 000 111 100 001
|
| 34
| 179
| 0 000 010 110 011
| 11
| 524
| 0 001 000 001 100
|
| 33
| 184
| 0 000 010 111 000
| 10
| 576
| 0 001 001 000 000
|
| 32
| 189
| 0 000 010 111 101
| 9
| 639
| 0 001 001 111 111
|
| 31
| 194
| 0 000 011 000 010
| 8
| 719
| 0 001 011 001 111
|
| 30
| 200
| 0 000 011 001 000
| 7
| 821
| 0 001 100 110 101
|
| 29
| 206
| 0 000 011 001 110
| 6
| 957
| 0 001 110 111 101
|
| 28
| 213
| 0 000 011 010 101
| 5
| 1147
| 0 010 001 111 011
|
| 27
| 220
| 0 000 011 011 100
| 4
| 1434
| 0 010 110 011 010
|
| 26
| 228
| 0 000 011 100 100
| 3
| 1911
| 0 011 101 110 111
|
| 25
| 237
| 0 000 011 101 101
| 2
| 2865
| 0 101 100 110 001
|
| 24
| 246
| 0 000 011 110 110
| 1
| 5730
| 1 011 001 100 010
|
| 23
| 256
| 0 000 100 000 000
|
|
|
|
|
| |  |
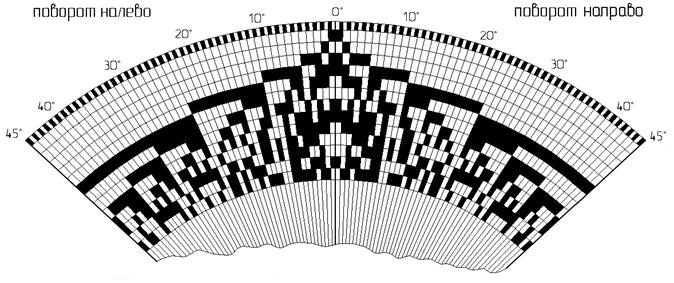
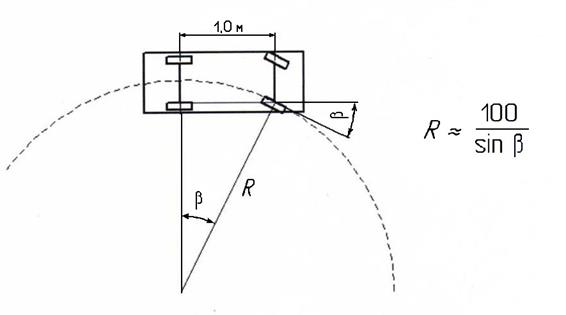
Рис.4. Кодовая шкала датчика радиуса поворота робокара (а) и схема взаимосвязи угла β с радиусом R поворота тележки робокара (б).
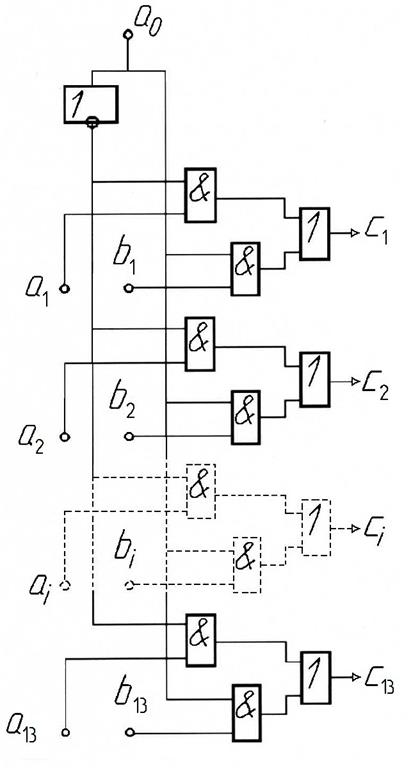
Рис 5. Система считывания кода со шкалы
регулятор. Во избежание ошибок считывания при переходе от одной кодовой комбинации к другой (ошибок граничного считывания), в датчике применён метод двойного считывающего элемента [6]. В данном случае он реализован следующим образом. К шкале добавлена вспомогательная дорожка, на которой имеются магнитные метки, по ширине равные половине дискреты датчика (0,5 град) и расположенные с таким же интервалом. Каждая метка нанесена так, что одна её граница совпадает с границей дискреты датчика, а другая граница – с серединой дискреты. Чтение меток со вспомога-тельной дорожки производится головкой а0. Головки считывания кода а1, а2, ..., а13 с основных дорожек шкалы продублированы головками b1, b2, ...,b13, причём все они расположены радиально двумя рядами, и расстояние между рядами составляет – 0,2–0,3 дискреты. В процессе работы датчика при переходе от одной кодовой комбинации к соседней на выходе головки а0 сигнал «0» меняется на «1». В то время, как предыдущая комбинация считывалась головками а1, а2, ..., а13, следующая за ней будет считываться головками b1, b2,..., b13. Когда метка, считываемая головкой а0, закончится, эта головка выполнит обратное переключение. В результате на выходах датчика с1, с2, ..., с13 никогда не появятся ложные комбинации, которые могут возникать на границах между дискретами из-за погрешностей изготовления датчика.
Остальные блоки системы построены известным образом, например, как описано в работе [7].
Поскольку разработанная система управления скоростью робокара достаточно проста, затраты на её изготовление невелики. Между тем, в сочетании с системой управления траекторией движения робокара, она может повысить его производительность в 2 раза.
Библиографический список
1. Гибкие производственные комплексы/ Под ред. П.Н.Белянина и В.А.Лещенко. М.: Машиностроение, 1984. 384 с.
2. Волчкевич Л.И., Усов Б.А. Транспортно- накопительные системы ГПС. М.: Высш. шк., 1989. 109 с.
3. Гибкое автоматическое производство/ В.О.Азбель, В.А.Егоров, А.Ю.Звоницкий и др. Л.: Машиностроение, 1985. 454 с.
4. Белов М.П., Новиков В.А., Рассудов Л.Н. Автоматизированный электропривод типовых производственных механизмов и технологических комплексов. М.: Изд. Центр «Академия», 2004. 576 с.
5. Леоненков А.В. Нечёткое моделирование в среде MATLAB и fuzzyTECH. Спб.: БХВ-Петербург, 2005. 736 с.
6. Преобразование информации для ЭЦВМ/ Б.В.Анисимов, В.Н.Четвериков. М.: Высш. шк., 1968. 333 с.
7. Шляндин В.М. Цифровые измерительные преобразователи и приборы. М.: Высш. шк., 1973. 280 с.
J. L. Liberman, M. S. Antropov
SYSTEM OF FUZZY-CONTROL ROBOCAR SPEED



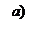
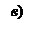

 Рис. 1. Графики функций принадлежности:
Рис. 1. Графики функций принадлежности: Матрица правил
Матрица правил