СТАТИСТИЧЕСКАЯ ФИЗИКА
Распределение Гиббса
Вывод распределения Гиббса.
Распределение Гиббса (Джозайя Уиллард Гиббс (1839 – 1903) - выдающийся американский физик и математик) определяет вероятность обнаружить макроскопическое тело, находящееся в термодинамическом равновесии с окружающей средой, в состоянии с заданной энергией 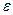 .
.
6.1. Функция распределения Гиббса.
Задачей настоящего параграфа является нахождение явного вида функции распределения 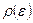 или
или  .
.
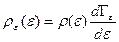 . (6.1)
. (6.1)
Эта функция описывает состояние макроскопического равновесного тела (подсистемы), помещенного в окружающую среду (другую подсистему) и образующего с этой средой замкнутую систему.
Сформулируем предварительные договоренности, на которые
 мы будем опираться, решая поставленную задачу.
мы будем опираться, решая поставленную задачу.
Предполагается, что взаимодействием тела с окружающей
средой в полном балансе энергий можно пренебречь. Тогда тело и
окружающую среду можно считать квазинезависимыми
(квазизамкнутыми) подсистемами, и полная энергия замкнутой
системы определяется как
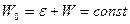 ,
,
где 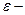 энергия тела,
энергия тела, 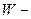 энергия среды.
энергия среды.
Далее, пусть размер рассматриваемой подсистемы (тела)
значительно меньше размера всей системы. Тогда число частиц 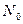 в полной системе и
в полной системе и  в малой подсистеме связаны соотношением:
в малой подсистеме связаны соотношением:
 .
.
В макроскопических телах флуктуации энергии в состоянии равновесия малы (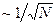 ). Поэтому под энергией
). Поэтому под энергией  подсистемы можно понимать её среднее значение
подсистемы можно понимать её среднее значение 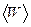 . В дальнейшем, если это не может привести к недоразумениям, знак усреднения
. В дальнейшем, если это не может привести к недоразумениям, знак усреднения 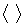 мы будем опускать, подразумевая, что для больших систем в состоянии равновесия рассматриваются средние значения их энергии.
мы будем опускать, подразумевая, что для больших систем в состоянии равновесия рассматриваются средние значения их энергии.
Примечание: следует понимать, что, вообще говоря, для любой подсистемы мы не можем таким образом использовать среднее значение ее энергии, т.к. в качестве подсистемы можно выбрать и 1 молекулу, а тогда флуктуации энергии могут быть велики.
Нас интересует вероятность  такого состояния тела, при котором его энергия заключена в пределах от
такого состояния тела, при котором его энергия заключена в пределах от 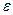 до
до 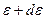 , в то время как окружающая среда находится в равновесном макроскопическом состоянии со средней энергией
, в то время как окружающая среда находится в равновесном макроскопическом состоянии со средней энергией  .
.
Это состояние среды можно описать фазовым объемом  . Напомним, что среда подавляющую часть времени находится в состоянии с энергией вблизи её среднего значения, поэтому условие нормировки может быть записано как
. Напомним, что среда подавляющую часть времени находится в состоянии с энергией вблизи её среднего значения, поэтому условие нормировки может быть записано как
 , (6.2)
, (6.2)
при этом статистический вес макроскопического состояния равен
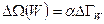 . (6.3)
. (6.3)
Фазовый объем  пропорционален числу способов, которыми энергия
пропорционален числу способов, которыми энергия 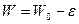 может быть распределена в окружающей тело среде.
может быть распределена в окружающей тело среде.
Так как тело и среда статистически независимы, то вероятность 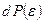 состояния, при котором энергия тела заключена в интервале
состояния, при котором энергия тела заключена в интервале 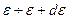 , пропорциональна произведению фазового объема
, пропорциональна произведению фазового объема 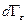 , описывающего состояние тела, и фазового объема, характеризующего макроскопическое состояние окружающей среды
, описывающего состояние тела, и фазового объема, характеризующего макроскопическое состояние окружающей среды  , и согласно теореме об умножении вероятностей:
, и согласно теореме об умножении вероятностей:
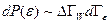 . (6.4)
. (6.4)
Фазовый объем, отвечающий равновесному состоянию окружающей среды, можно выразить через её энтропию (5.42):
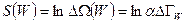 . (6.5)
. (6.5)
Отсюда
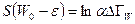
и 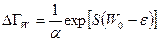 (6.6)
(6.6)
Подставляя в (6.4), получаем
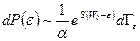 . (6.7)
. (6.7)
Проведенное несложное преобразование позволяет нам представить искомую вероятность как функцию лишь одной переменной 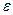 .
.
Учтем теперь, что тело составляет малую часть системы, т.е. 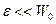 . Используя это условие, разложим энтропию среды
. Используя это условие, разложим энтропию среды  в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 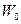 :
:
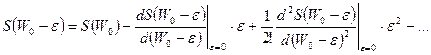 . (6.8)
. (6.8)
Ограничимся в разложении членом первого порядка по энергии 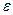 (пренебрегая членами разложения более высокого порядка, мы совершаем ошибку порядка
(пренебрегая членами разложения более высокого порядка, мы совершаем ошибку порядка  ) и используем выражение для температуры, полученное нами ранее в разделе «Термодинамика»:
) и используем выражение для температуры, полученное нами ранее в разделе «Термодинамика»:
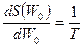 .
.
Тогда получаем
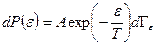 . (6.9)
. (6.9)
Здесь 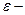 энергия изучаемого тела, зависящая от координат и скоростей составляющих его атомов или молекул. Константа
энергия изучаемого тела, зависящая от координат и скоростей составляющих его атомов или молекул. Константа  включает все постоянные, не зависящие от энергии подсистемы (в частности,
включает все постоянные, не зависящие от энергии подсистемы (в частности, 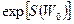 ,
, 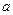 и коэффициент пропорциональности). Постоянную
и коэффициент пропорциональности). Постоянную  можно найти из условия нормировки:
можно найти из условия нормировки:
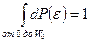 .
.
Подставляя сюда (6.9), получаем
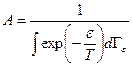 . (6.10)
. (6.10)
Наконец, сравнивая выражение (6.9) для вероятности макроскопического состояния тела с энергией 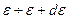 и выражение (5.29) (где
и выражение (5.29) (где 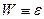 ):
):
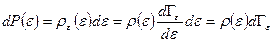 ,
,
получаем выражение для плотности вероятности - функцию статистического распределения, или распределение Гиббса:
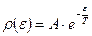 (6.11)
(6.11)
Формула (6.11) дает распределение по энергиям вероятностей различных микроскопических состояний подсистемы, являющейся малой частью некоторой большой замкнутой системы. Это распределение было найдено Гиббсом в 1901 году.
Используя распределение Гиббса, можно определить среднее значение физической величины, зависящей от координат и импульсов 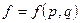 :
:
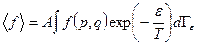 . (6.12)
. (6.12)
6.2. Свободная энергия в распределении Гиббса.
Ранее, (5.42), мы установили связь энтропии  подсистемы с соответствующим её макросостоянию фазовым объемом:
подсистемы с соответствующим её макросостоянию фазовым объемом:
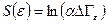 ,
,
где, напомним,  размерный коэффициент пропорциональности и
размерный коэффициент пропорциональности и 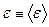 .
.
Поскольку подсистема практически все время проводит в фазовом объеме 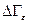 , то условие нормировки записывается в виде (5.38):
, то условие нормировки записывается в виде (5.38):
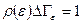 .
.
Из последних двух уравнений следует
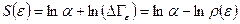 ,
,
или, для распределения Гиббса (6.11),
 . (6.13)
. (6.13)
Средняя энергия – это как раз то, что понимают под внутренней энергией подсистемы в термодинамике.
Перепишем выражение (6.13) в виде
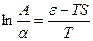 . (6.14)
. (6.14)
Вспоминая, что 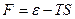 , получаем
, получаем
 , (6.15)
, (6.15)
т.е. нормировочная постоянная  в распределении Гиббса определяется через свободную энергию
в распределении Гиббса определяется через свободную энергию 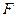 .
.
Тогда распределение Гиббса может быть записано в виде, в котором оно наиболее часто применяется
 . (6.16)
. (6.16)
Поскольку свободная энергия 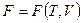 , характеризуя подсистему в целом, не зависит от скоростей и координат отдельных частиц подсистемы, то условие нормировки для функции (6.16) имеет вид
, характеризуя подсистему в целом, не зависит от скоростей и координат отдельных частиц подсистемы, то условие нормировки для функции (6.16) имеет вид
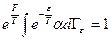 , (6.17)
, (6.17)
откуда
 . (6.18)
. (6.18)
Эта формула является наиболее важной для термодинамических применений распределения Гиббса, поскольку устанавливает связь функции состояния 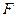 со статистическими характеристиками тела. Она, в принципе, позволяет вычислить термодинамические функции любого тела, если для него известна функция распределения по энергиям
со статистическими характеристиками тела. Она, в принципе, позволяет вычислить термодинамические функции любого тела, если для него известна функция распределения по энергиям 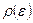 , или, как говорят, энергетический спектр.
, или, как говорят, энергетический спектр.
6.3. Уравнение состояния идеального газа.
Уравнение состояния идеального газа можно вывести, используя соотношение (6.18), выражающее свободную энергию через распределение Гиббса.
Поскольку в идеальном газе нет взаимодействия между молекулами, его полная энергия определяется лишь кинетической энергией хаотического движения молекул. Поэтому выражение (6.18) можно переписать в виде
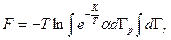 . (6.19)
. (6.19)
Если в рассматриваемом объеме 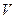 содержится
содержится 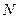 молекул, то по теореме умножения вероятностей:
молекул, то по теореме умножения вероятностей:
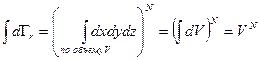 . (6.20)
. (6.20)
Подставляя последнее соотношение в (6.19), имеем
 . Записывая свободную энергию
. Записывая свободную энергию 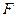 в такой форме, мы подчеркиваем тот факт, что интеграл, стоящий в круглых скобках, не зависит от объема и при дифференцировании по объему рассматривается как постоянная величина.
в такой форме, мы подчеркиваем тот факт, что интеграл, стоящий в круглых скобках, не зависит от объема и при дифференцировании по объему рассматривается как постоянная величина.
Из курса термодинамики известно, что
 .
.
Тогда
 ,
,
откуда
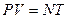 ;
; 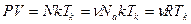 , или
, или 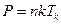 . (6.21)
. (6.21)
Т.о., мы получили уравнение состояния идеального газа – уравнение Менделеева-Клапейрона – из статистических соображений.
6.4. Распределения по кинетическим и потенциальным энергиям.
В классической физике полная энергия 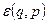 всегда может быть представлена как сумма кинетической
всегда может быть представлена как сумма кинетической 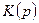 и потенциальной
и потенциальной 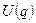 энергий:
энергий:
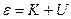 , (6.22)
, (6.22)
где 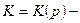 квадратичная функция импульсов (скоростей), а
квадратичная функция импульсов (скоростей), а 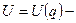 функция координат системы, вид которой, вообще говоря, зависит от закона взаимодействия атомов между собой и от внешнего поля (потенциальной энергии во внешнем поле), если таковое имеется.
функция координат системы, вид которой, вообще говоря, зависит от закона взаимодействия атомов между собой и от внешнего поля (потенциальной энергии во внешнем поле), если таковое имеется.
При таком подходе элемент фазового объема можно представить в виде произведения двух элементов:
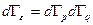 , (6.23)
, (6.23)
где 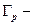 элемент фазового объема в пространстве импульсов (скоростей),
элемент фазового объема в пространстве импульсов (скоростей), 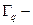 элемент фазового объема в пространстве координат.
элемент фазового объема в пространстве координат.
Тогда вероятность искомого события записывается в виде
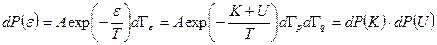 , (6.24)
, (6.24)
т.е. представляется в виде произведения двух независимых сомножителей:
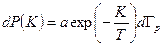 ,
,
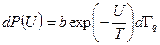 .
.
Это означает, что вероятность иметь определенные значения кинетической энергии никак не влияет на вероятность иметь одновременно какие-то значения потенциальной энергии. Поэтому вероятности  и
и 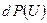 должны удовлетворять независимым условиям нормировки для определения постоянных
должны удовлетворять независимым условиям нормировки для определения постоянных 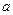 и
и 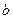 .
.
Заметим, что такое разбиение на независимые распределения по кинетическим и потенциальным энергиям возможно лишь в классической физике. При квантовом рассмотрении задачи вероятности различных значений координат и импульсов оказываются связанными друг с другом соотношением неопределенностей.
СТАТИСТИЧЕСКАЯ ФИЗИКА
Распределение Гиббса
Вывод распределения Гиббса.
Распределение Гиббса (Джозайя Уиллард Гиббс (1839 – 1903) - выдающийся американский физик и математик) определяет вероятность обнаружить макроскопическое тело, находящееся в термодинамическом равновесии с окружающей средой, в состоянии с заданной энергией 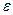 .
.
6.1. Функция распределения Гиббса.
Задачей настоящего параграфа является нахождение явного вида функции распределения 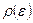 или
или  .
.
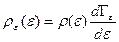 . (6.1)
. (6.1)
Эта функция описывает состояние макроскопического равновесного тела (подсистемы), помещенного в окружающую среду (другую подсистему) и образующего с этой средой замкнутую систему.
Сформулируем предварительные договоренности, на которые
 мы будем опираться, решая поставленную задачу.
мы будем опираться, решая поставленную задачу.
Предполагается, что взаимодействием тела с окружающей
средой в полном балансе энергий можно пренебречь. Тогда тело и
окружающую среду можно считать квазинезависимыми
(квазизамкнутыми) подсистемами, и полная энергия замкнутой
системы определяется как
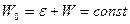 ,
,
где 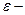 энергия тела,
энергия тела, 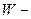 энергия среды.
энергия среды.
Далее, пусть размер рассматриваемой подсистемы (тела)
значительно меньше размера всей системы. Тогда число частиц 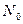 в полной системе и
в полной системе и  в малой подсистеме связаны соотношением:
в малой подсистеме связаны соотношением:
 .
.
В макроскопических телах флуктуации энергии в состоянии равновесия малы (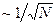 ). Поэтому под энергией
). Поэтому под энергией  подсистемы можно понимать её среднее значение
подсистемы можно понимать её среднее значение 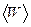 . В дальнейшем, если это не может привести к недоразумениям, знак усреднения
. В дальнейшем, если это не может привести к недоразумениям, знак усреднения 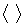 мы будем опускать, подразумевая, что для больших систем в состоянии равновесия рассматриваются средние значения их энергии.
мы будем опускать, подразумевая, что для больших систем в состоянии равновесия рассматриваются средние значения их энергии.
Примечание: следует понимать, что, вообще говоря, для любой подсистемы мы не можем таким образом использовать среднее значение ее энергии, т.к. в качестве подсистемы можно выбрать и 1 молекулу, а тогда флуктуации энергии могут быть велики.
Нас интересует вероятность  такого состояния тела, при котором его энергия заключена в пределах от
такого состояния тела, при котором его энергия заключена в пределах от 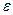 до
до 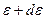 , в то время как окружающая среда находится в равновесном макроскопическом состоянии со средней энергией
, в то время как окружающая среда находится в равновесном макроскопическом состоянии со средней энергией  .
.
Это состояние среды можно описать фазовым объемом  . Напомним, что среда подавляющую часть времени находится в состоянии с энергией вблизи её среднего значения, поэтому условие нормировки может быть записано как
. Напомним, что среда подавляющую часть времени находится в состоянии с энергией вблизи её среднего значения, поэтому условие нормировки может быть записано как
 , (6.2)
, (6.2)
при этом статистический вес макроскопического состояния равен
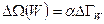 . (6.3)
. (6.3)
Фазовый объем  пропорционален числу способов, которыми энергия
пропорционален числу способов, которыми энергия 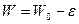 может быть распределена в окружающей тело среде.
может быть распределена в окружающей тело среде.
Так как тело и среда статистически независимы, то вероятность 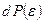 состояния, при котором энергия тела заключена в интервале
состояния, при котором энергия тела заключена в интервале 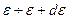 , пропорциональна произведению фазового объема
, пропорциональна произведению фазового объема 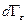 , описывающего состояние тела, и фазового объема, характеризующего макроскопическое состояние окружающей среды
, описывающего состояние тела, и фазового объема, характеризующего макроскопическое состояние окружающей среды  , и согласно теореме об умножении вероятностей:
, и согласно теореме об умножении вероятностей:
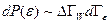 . (6.4)
. (6.4)
Фазовый объем, отвечающий равновесному состоянию окружающей среды, можно выразить через её энтропию (5.42):
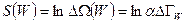 . (6.5)
. (6.5)
Отсюда
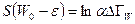
и 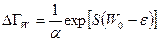 (6.6)
(6.6)
Подставляя в (6.4), получаем
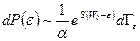 . (6.7)
. (6.7)
Проведенное несложное преобразование позволяет нам представить искомую вероятность как функцию лишь одной переменной 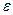 .
.
Учтем теперь, что тело составляет малую часть системы, т.е. 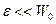 . Используя это условие, разложим энтропию среды
. Используя это условие, разложим энтропию среды  в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 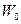 :
:
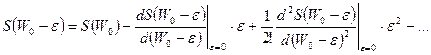 . (6.8)
. (6.8)
Ограничимся в разложении членом первого порядка по энергии 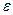 (пренебрегая членами разложения более высокого порядка, мы совершаем ошибку порядка
(пренебрегая членами разложения более высокого порядка, мы совершаем ошибку порядка  ) и используем выражение для температуры, полученное нами ранее в разделе «Термодинамика»:
) и используем выражение для температуры, полученное нами ранее в разделе «Термодинамика»:
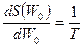 .
.
Тогда получаем
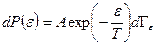 . (6.9)
. (6.9)
Здесь 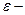 энергия изучаемого тела, зависящая от координат и скоростей составляющих его атомов или молекул. Константа
энергия изучаемого тела, зависящая от координат и скоростей составляющих его атомов или молекул. Константа  включает все постоянные, не зависящие от энергии подсистемы (в частности,
включает все постоянные, не зависящие от энергии подсистемы (в частности, 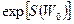 ,
, 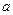 и коэффициент пропорциональности). Постоянную
и коэффициент пропорциональности). Постоянную  можно найти из условия нормировки:
можно найти из условия нормировки:
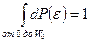 .
.
Подставляя сюда (6.9), получаем
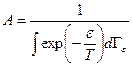 . (6.10)
. (6.10)
Наконец, сравнивая выражение (6.9) для вероятности макроскопического состояния тела с энергией 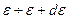 и выражение (5.29) (где
и выражение (5.29) (где 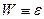 ):
):
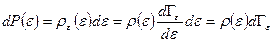 ,
,
получаем выражение для плотности вероятности - функцию статистического распределения, или распределение Гиббса:
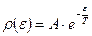 (6.11)
(6.11)
Формула (6.11) дает распределение по энергиям вероятностей различных микроскопических состояний подсистемы, являющейся малой частью некоторой большой замкнутой системы. Это распределение было найдено Гиббсом в 1901 году.
Используя распределение Гиббса, можно определить среднее значение физической величины, зависящей от координат и импульсов 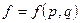 :
:
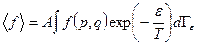 . (6.12)
. (6.12)
6.2. Свободная энергия в распределении Гиббса.
Ранее, (5.42), мы установили связь энтропии  подсистемы с соответствующим её макросостоянию фазовым объемом:
подсистемы с соответствующим её макросостоянию фазовым объемом:
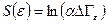 ,
,
где, напомним,  размерный коэффициент пропорциональности и
размерный коэффициент пропорциональности и 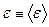 .
.
Поскольку подсистема практически все время проводит в фазовом объеме 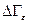 , то условие нормировки записывается в виде (5.38):
, то условие нормировки записывается в виде (5.38):
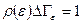 .
.
Из последних двух уравнений следует
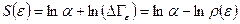 ,
,
или, для распределения Гиббса (6.11),
 . (6.13)
. (6.13)
Средняя энергия – это как раз то, что понимают под внутренней энергией подсистемы в термодинамике.
Перепишем выражение (6.13) в виде
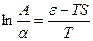 . (6.14)
. (6.14)
Вспоминая, что 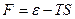 , получаем
, получаем
 , (6.15)
, (6.15)
т.е. нормировочная постоянная  в распределении Гиббса определяется через свободную энергию
в распределении Гиббса определяется через свободную энергию 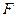 .
.
Тогда распределение Гиббса может быть записано в виде, в котором оно наиболее часто применяется
 . (6.16)
. (6.16)
Поскольку свободная энергия 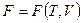 , характеризуя подсистему в целом, не зависит от скоростей и координат отдельных частиц подсистемы, то условие нормировки для функции (6.16) имеет вид
, характеризуя подсистему в целом, не зависит от скоростей и координат отдельных частиц подсистемы, то условие нормировки для функции (6.16) имеет вид
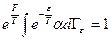 , (6.17)
, (6.17)
откуда
 . (6.18)
. (6.18)
Эта формула является наиболее важной для термодинамических применений распределения Гиббса, поскольку устанавливает связь функции состояния 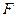 со статистическими характеристиками тела. Она, в принципе, позволяет вычислить термодинамические функции любого тела, если для него известна функция распределения по энергиям
со статистическими характеристиками тела. Она, в принципе, позволяет вычислить термодинамические функции любого тела, если для него известна функция распределения по энергиям 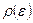 , или, как говорят, энергетический спектр.
, или, как говорят, энергетический спектр.
6.3. Уравнение состояния идеального газа.
Уравнение состояния идеального газа можно вывести, используя соотношение (6.18), выражающее свободную энергию через распределение Гиббса.
Поскольку в идеальном газе нет взаимодействия между молекулами, его полная энергия определяется лишь кинетической энергией хаотического движения молекул. Поэтому выражение (6.18) можно переписать в виде
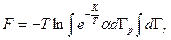 . (6.19)
. (6.19)
Если в рассматриваемом объеме 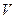 содержится
содержится 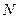 молекул, то по теореме умножения вероятностей:
молекул, то по теореме умножения вероятностей:
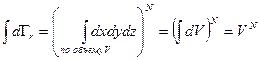 . (6.20)
. (6.20)
Подставляя последнее соотношение в (6.19), имеем
 . Записывая свободную энергию
. Записывая свободную энергию 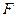 в такой форме, мы подчеркиваем тот факт, что интеграл, стоящий в круглых скобках, не зависит от объема и при дифференцировании по объему рассматривается как постоянная величина.
в такой форме, мы подчеркиваем тот факт, что интеграл, стоящий в круглых скобках, не зависит от объема и при дифференцировании по объему рассматривается как постоянная величина.
Из курса термодинамики известно, что
 .
.
Тогда
 ,
,
откуда
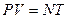 ;
; 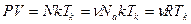 , или
, или 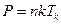 . (6.21)
. (6.21)
Т.о., мы получили уравнение состояния идеального газа – уравнение Менделеева-Клапейрона – из статистических соображений.
6.4. Распределения по кинетическим и потенциальным энергиям.
В классической физике полная энергия 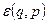 всегда может быть представлена как сумма кинетической
всегда может быть представлена как сумма кинетической 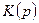 и потенциальной
и потенциальной 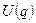 энергий:
энергий:
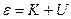 , (6.22)
, (6.22)
где 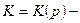 квадратичная функция импульсов (скоростей), а
квадратичная функция импульсов (скоростей), а 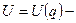 функция координат системы, вид которой, вообще говоря, зависит от закона взаимодействия атомов между собой и от внешнего поля (потенциальной энергии во внешнем поле), если таковое имеется.
функция координат системы, вид которой, вообще говоря, зависит от закона взаимодействия атомов между собой и от внешнего поля (потенциальной энергии во внешнем поле), если таковое имеется.
При таком подходе элемент фазового объема можно представить в виде произведения двух элементов:
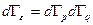 , (6.23)
, (6.23)
где 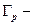 элемент фазового объема в пространстве импульсов (скоростей),
элемент фазового объема в пространстве импульсов (скоростей), 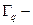 элемент фазового объема в пространстве координат.
элемент фазового объема в пространстве координат.
Тогда вероятность искомого события записывается в виде
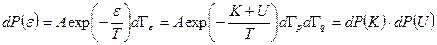 , (6.24)
, (6.24)
т.е. представляется в виде произведения двух независимых сомножителей:
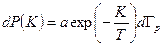 ,
,
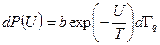 .
.
Это означает, что вероятность иметь определенные значения кинетической энергии никак не влияет на вероятность иметь одновременно какие-то значения потенциальной энергии. Поэтому вероятности 
|
|
|



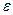 .
.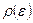 или
или  .
.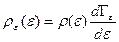 . (6.1)
. (6.1) мы будем опираться, решая поставленную задачу.
мы будем опираться, решая поставленную задачу. 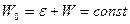 ,
,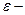 энергия тела,
энергия тела, 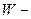 энергия среды.
энергия среды. 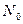 в полной системе и
в полной системе и  в малой подсистеме связаны соотношением:
в малой подсистеме связаны соотношением: .
.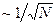 ). Поэтому под энергией
). Поэтому под энергией  подсистемы можно понимать её среднее значение
подсистемы можно понимать её среднее значение 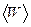 . В дальнейшем, если это не может привести к недоразумениям, знак усреднения
. В дальнейшем, если это не может привести к недоразумениям, знак усреднения 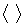 мы будем опускать, подразумевая, что для больших систем в состоянии равновесия рассматриваются средние значения их энергии.
мы будем опускать, подразумевая, что для больших систем в состоянии равновесия рассматриваются средние значения их энергии.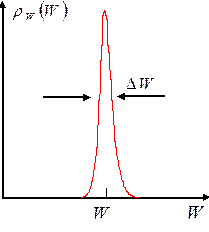
 такого состояния тела, при котором его энергия заключена в пределах от
такого состояния тела, при котором его энергия заключена в пределах от 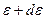 , в то время как окружающая среда находится в равновесном макроскопическом состоянии со средней энергией
, в то время как окружающая среда находится в равновесном макроскопическом состоянии со средней энергией  . Напомним, что среда подавляющую часть времени находится в состоянии с энергией вблизи её среднего значения, поэтому условие нормировки может быть записано как
. Напомним, что среда подавляющую часть времени находится в состоянии с энергией вблизи её среднего значения, поэтому условие нормировки может быть записано как , (6.2)
, (6.2)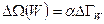 . (6.3)
. (6.3)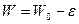 может быть распределена в окружающей тело среде.
может быть распределена в окружающей тело среде.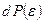 состояния, при котором энергия тела заключена в интервале
состояния, при котором энергия тела заключена в интервале 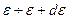 , пропорциональна произведению фазового объема
, пропорциональна произведению фазового объема 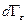 , описывающего состояние тела, и фазового объема, характеризующего макроскопическое состояние окружающей среды
, описывающего состояние тела, и фазового объема, характеризующего макроскопическое состояние окружающей среды 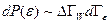 . (6.4)
. (6.4)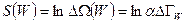 . (6.5)
. (6.5)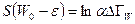
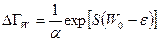 (6.6)
(6.6)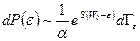 . (6.7)
. (6.7)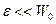 . Используя это условие, разложим энтропию среды
. Используя это условие, разложим энтропию среды  в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 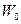 :
: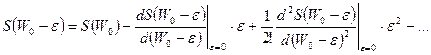 . (6.8)
. (6.8) ) и используем выражение для температуры, полученное нами ранее в разделе «Термодинамика»:
) и используем выражение для температуры, полученное нами ранее в разделе «Термодинамика»: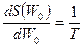 .
. 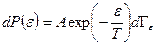 . (6.9)
. (6.9) включает все постоянные, не зависящие от энергии подсистемы (в частности,
включает все постоянные, не зависящие от энергии подсистемы (в частности, 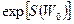 ,
, 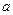 и коэффициент пропорциональности). Постоянную
и коэффициент пропорциональности). Постоянную 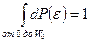 .
.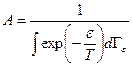 . (6.10)
. (6.10)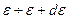 и выражение (5.29) (где
и выражение (5.29) (где 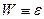 ):
):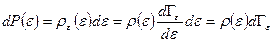 ,
,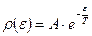 (6.11)
(6.11)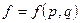 :
: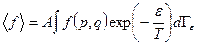 . (6.12)
. (6.12) подсистемы с соответствующим её макросостоянию фазовым объемом:
подсистемы с соответствующим её макросостоянию фазовым объемом: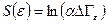 ,
, размерный коэффициент пропорциональности и
размерный коэффициент пропорциональности и 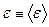 .
.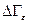 , то условие нормировки записывается в виде (5.38):
, то условие нормировки записывается в виде (5.38):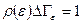 .
.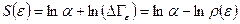 ,
, . (6.13)
. (6.13)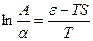 . (6.14)
. (6.14) 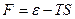 , получаем
, получаем , (6.15)
, (6.15)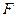 .
.  . (6.16)
. (6.16)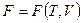 , характеризуя подсистему в целом, не зависит от скоростей и координат отдельных частиц подсистемы, то условие нормировки для функции (6.16) имеет вид
, характеризуя подсистему в целом, не зависит от скоростей и координат отдельных частиц подсистемы, то условие нормировки для функции (6.16) имеет вид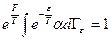 , (6.17)
, (6.17) . (6.18)
. (6.18)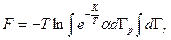 . (6.19)
. (6.19)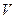 содержится
содержится 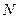 молекул, то по теореме умножения вероятностей:
молекул, то по теореме умножения вероятностей: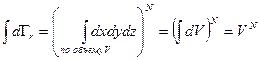 . (6.20)
. (6.20) . Записывая свободную энергию
. Записывая свободную энергию  .
.  ,
,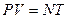 ;
; 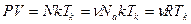 , или
, или 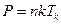 . (6.21)
. (6.21) 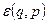 всегда может быть представлена как сумма кинетической
всегда может быть представлена как сумма кинетической 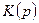 и потенциальной
и потенциальной 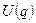 энергий:
энергий: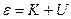 , (6.22)
, (6.22)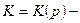 квадратичная функция импульсов (скоростей), а
квадратичная функция импульсов (скоростей), а 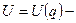 функция координат системы, вид которой, вообще говоря, зависит от закона взаимодействия атомов между собой и от внешнего поля (потенциальной энергии во внешнем поле), если таковое имеется.
функция координат системы, вид которой, вообще говоря, зависит от закона взаимодействия атомов между собой и от внешнего поля (потенциальной энергии во внешнем поле), если таковое имеется.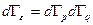 , (6.23)
, (6.23)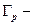 элемент фазового объема в пространстве импульсов (скоростей),
элемент фазового объема в пространстве импульсов (скоростей), 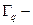 элемент фазового объема в пространстве координат.
элемент фазового объема в пространстве координат.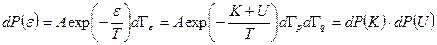 , (6.24)
, (6.24) 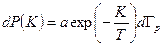 ,
,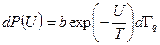 .
. и
и 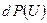 должны удовлетворять независимым условиям нормировки для определения постоянных
должны удовлетворять независимым условиям нормировки для определения постоянных 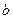 .
.


