5.1. Распределение Максвелла-Больцмана
В начале настоящей главы мы установили, что для классической подсистемы её энергия может быть представлена в виде суммы двух независимых слагаемых:
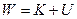 ,
,
поскольку кинетическая энергия есть функция импульсов (скоростей) частиц, а потенциальная энергия - функция координат. Поэтому вероятность для подсистемы находиться в состоянии с энергией  определяется как
определяется как
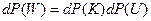 . (5.1)
. (5.1)
Используя распределение Гиббса, мы можем записать, что вероятность молекуле находиться в состоянии с энергией 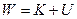 при определенных значениях координат и проекций импульсов есть
при определенных значениях координат и проекций импульсов есть
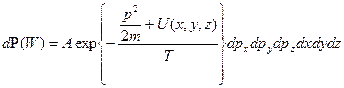 . (5.2)
. (5.2)
Выраженное таким образом распределение вероятностей для одной частицы называется распределением Максвелла-Больцмана.
Средняя энергия, приходящаяся на колебательную степень свободы. Закон Дюлонга и Пти.
Распределение Максвелла-Больцмана позволяет найти теплоемкость 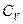 твердых тел при достаточно высоких температурах
твердых тел при достаточно высоких температурах  , для которых применимо классическое описание.
, для которых применимо классическое описание.
Твердое тело – макроскопическая система, состояние которой определяется средними значениями соответствующих параметров. Рассмотрим кристаллическое твердое тело. Равновесное состояние кристалла – периодическое расположение атомов в пространстве. Однако, атомы не находятся в покое, они совершают малые тепловые колебания относительно положений равновесия. Рассмотрим колебания, совершаемые атомом вдоль оси 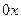 . Энергия такого осциллятора в любой момент времени определяется выражением:
. Энергия такого осциллятора в любой момент времени определяется выражением:
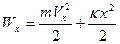
где 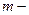 масса атома,
масса атома, 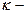 упругая постоянная.
упругая постоянная.
Статистическое описание движения атома с энергией 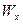 можно дать с помощью распределения Максвелла-Больцмана, которое для отдельного осциллятора имеет вид:
можно дать с помощью распределения Максвелла-Больцмана, которое для отдельного осциллятора имеет вид:
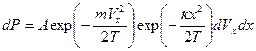
Здесь  – нормировочная постоянная, выражаемая через произведение 2-х постоянных:
– нормировочная постоянная, выражаемая через произведение 2-х постоянных: 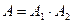 , которые равны, соответственно
, которые равны, соответственно
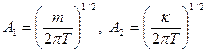 .
.
Теперь мы можем сосчитать среднюю энергию осциллятора, совершающего колебания вдоль оси  :
:
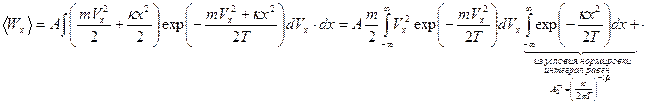
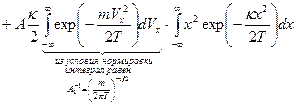 .
.
Выше, используя интеграл Пуассона, мы получили
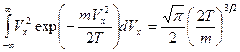 ,
,
аналогично
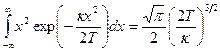 .
.
Таким образом,
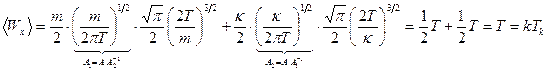 .
.
Итак, на одну колебательную степень свободы приходится энергия 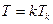 . Из расчета видно, что первое слагаемое
. Из расчета видно, что первое слагаемое 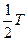 возникает при усреднении кинетической энергии колебательного движения, а второе слагаемое
возникает при усреднении кинетической энергии колебательного движения, а второе слагаемое 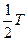 обусловлено потенциальной энергией колебательного движения.
обусловлено потенциальной энергией колебательного движения.
Здесь мы окончательно доказали теорему о равномерном распределении энергии по степеням свободы, согласно которой на каждую колебательную степень свободы приходится энергия  (ранее было показано, что на поступательную или вращательную степени свободы приходилось по
(ранее было показано, что на поступательную или вращательную степени свободы приходилось по 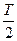 ).
).
Если представить колебательное движение атомов в кристалле в виде совокупности независимых движений вдоль трех ортогональных осей 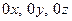 , то средняя энергия колебаний одного атома равна
, то средняя энергия колебаний одного атома равна
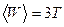 ,
,
Если рассматривать 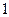 моль вещества, содержащий
моль вещества, содержащий 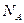 молекул, то
молекул, то
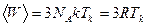 ,
,
где температура 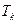 измеряется в Кельвинах.
измеряется в Кельвинах.
Суммарная энергия осцилляторов играет роль внутренней энергии, определенной в термодинамике, поэтому молярная теплоемкость 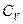 твердого тела при постоянном объеме оказывается равной
твердого тела при постоянном объеме оказывается равной
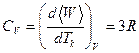 .
.
Т.о., мы пришли к правилу, которое было установлено опытным путем и получило название закона Дюлонга и Пти:
Молярная теплоемкость всех твердых тел при высоких температурах (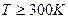 ) не зависит от температуры и равна
) не зависит от температуры и равна 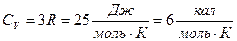 .
.
5.2. Распределение Больцмана.
Пусть интересующая нас подсистема (газ) находится во внешнем поле, в котором потенциальная энергия молекулы 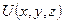 есть функция только её координат (например, гравитационное поле).
есть функция только её координат (например, гравитационное поле).
Основываясь на соотношении (5.1), т.е. в силу независимости событий иметь определенные значения как кинетической, так и потенциальной энергий, можно рассмотреть отдельно распределение частиц во внешнем поле 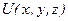 :
:
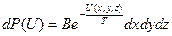 , (5.3)
, (5.3)
что дает вероятность нахождения частицы в объеме 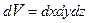 вблизи точки с координатами
вблизи точки с координатами 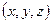 .
.
Пусть 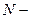 полное число молекул в подсистеме. Так как
полное число молекул в подсистеме. Так как
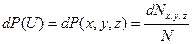 ,
,
то число молекул в элементе пространственного объема 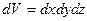 определяется формулой:
определяется формулой:
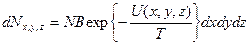 (5.4)
(5.4)
Смысл множителя 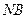 легко установить, если ввести число частиц в единице объема, т.е. концентрацию частиц (плотность числа частиц):
легко установить, если ввести число частиц в единице объема, т.е. концентрацию частиц (плотность числа частиц):
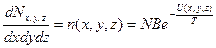 (5.5)
(5.5)
Тогда, очевидно, что произведение 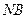 равно плотности числа частиц в точках, где
равно плотности числа частиц в точках, где 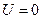 , т.е.
, т.е. 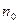 .
.
Тогда выражение (5.5) принимает вид
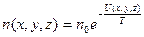 (5.6)
(5.6)
Полученная формула носит название распределения Больцмана.
Примечание: если отсчет идет от точки, где 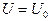 , тогда распределение Больцмана имеет вид:
, тогда распределение Больцмана имеет вид:
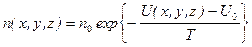 (5.7)
(5.7)
Примеры применения распределения Больцмана.
1). Распределение частиц в сосуде по высоте в однородном поле тяжести (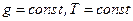 ).
).
Для Земли поле силы тяжести может считаться однородным для небольших высот  (
(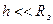 ), где
), где 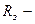 радиус Земли. Воспользуемся малостью
радиус Земли. Воспользуемся малостью  и разложим в ряд потенциальную энергию молекулы, ограничившись первыми двумя слагаемыми:
и разложим в ряд потенциальную энергию молекулы, ограничившись первыми двумя слагаемыми:
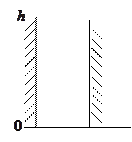
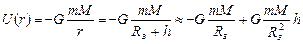 ,
,
Тогда
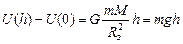
Используя распределение Больцмана, можем записать
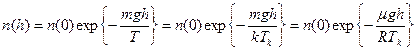 (5.8)
(5.8)
Здесь 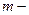 масса молекулы;
масса молекулы; 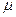 - молярная масса газа,
- молярная масса газа, 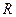 - универсальная газовая постоянная.
- универсальная газовая постоянная.
Воспользовавшись связью между концентрацией газа и давлением, получаем известную барометрическую формулу Больцмана:
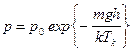 (5.9)
(5.9)
Концентрация частиц убывает с высотой, причем концентрация более тяжелых частиц убывает с высотой быстрее. Это создает подъемную силу (для более легких объектов - воздушные шары).
Для более высоких температур распределение по высоте становится более равномерным (см. рисунок), однако полное число частиц 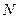 в ограниченном объеме постоянно:
в ограниченном объеме постоянно:
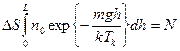 .
.
Здесь 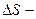 площадь сечения “сосуда”, а
площадь сечения “сосуда”, а 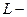 его полная высота.
его полная высота.
2). Распределение частиц во вращающемся сосуде.
Пусть сосуд, наполненный газом, вращается вокруг оси 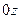 с постоянной угловой скоростью
с постоянной угловой скоростью 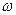 . Найдем распределение молекул в сосуде вдоль оси
. Найдем распределение молекул в сосуде вдоль оси 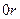 (в горизонтальной плоскости).
(в горизонтальной плоскости).
Перейдем в неинерциальную систему отсчета.
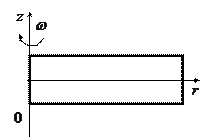 В НИСО на частицы действует центробежная сила инерции
В НИСО на частицы действует центробежная сила инерции
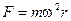 ,
,
а их потенциальная энергия определяется выражением:
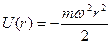 .
.
Тогда искомое распределение частиц имеет вид:
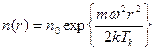 (5.10)
(5.10)
Таким образом, как следует из (5.10), концентрация молекул растет по мере удаления от оси вращения.
3). О распределении молекул в атмосфере планет.
Потенциальная энергия молекул в поле силы тяжести равна
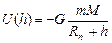
и в равновесном состоянии получаем следующее распределение:
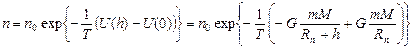 .
.
Однако, если бы это распределение было справедливо на любом расстоянии от планеты, то при 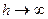 мы бы получили
мы бы получили
 ,
,
т.е. получаем конечное число для концентрации на бесконечности, что невозможно, т.к. объем вокруг планеты бесконечен, а общее число молекул в атмосфере конечно. Получаем, что равновесие возможно лишь при 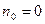 , т.е. атмосфера не должна быть в равновесии.
, т.е. атмосфера не должна быть в равновесии.
Отсюда вывод: невозможность существования равновесного состояния планетной атмосферы. Это связано с тем, что разность потенциальной энергии молекулы в поле тяготения планеты на поверхности и на бесконечности остается конечной.



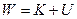 ,
, определяется как
определяется как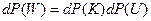 . (5.1)
. (5.1)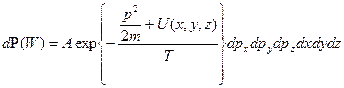 . (5.2)
. (5.2)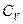 твердых тел при достаточно высоких температурах
твердых тел при достаточно высоких температурах  , для которых применимо классическое описание.
, для которых применимо классическое описание.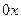 . Энергия такого осциллятора в любой момент времени определяется выражением:
. Энергия такого осциллятора в любой момент времени определяется выражением: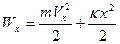
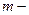 масса атома,
масса атома, 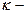 упругая постоянная.
упругая постоянная.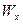 можно дать с помощью распределения Максвелла-Больцмана, которое для отдельного осциллятора имеет вид:
можно дать с помощью распределения Максвелла-Больцмана, которое для отдельного осциллятора имеет вид: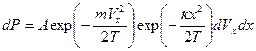
 – нормировочная постоянная, выражаемая через произведение 2-х постоянных:
– нормировочная постоянная, выражаемая через произведение 2-х постоянных: 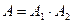 , которые равны, соответственно
, которые равны, соответственно 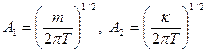 .
.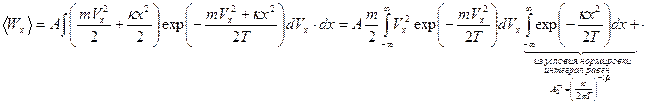
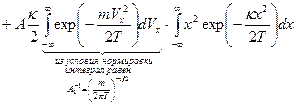 .
.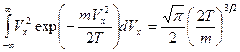 ,
,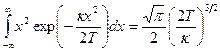 .
.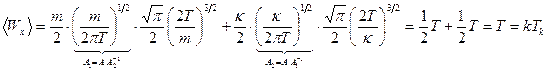 .
.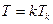 . Из расчета видно, что первое слагаемое
. Из расчета видно, что первое слагаемое 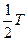 возникает при усреднении кинетической энергии колебательного движения, а второе слагаемое
возникает при усреднении кинетической энергии колебательного движения, а второе слагаемое 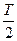 ).
).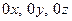 , то средняя энергия колебаний одного атома равна
, то средняя энергия колебаний одного атома равна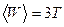 ,
,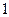 моль вещества, содержащий
моль вещества, содержащий 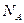 молекул, то
молекул, то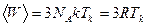 ,
,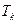 измеряется в Кельвинах.
измеряется в Кельвинах.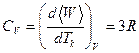 .
.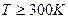 ) не зависит от температуры и равна
) не зависит от температуры и равна 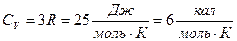 .
. 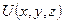 есть функция только её координат (например, гравитационное поле).
есть функция только её координат (например, гравитационное поле).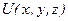 :
: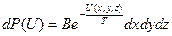 , (5.3)
, (5.3)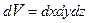 вблизи точки с координатами
вблизи точки с координатами 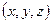 .
.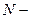 полное число молекул в подсистеме. Так как
полное число молекул в подсистеме. Так как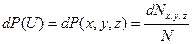 ,
, 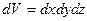 определяется формулой:
определяется формулой: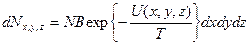 (5.4)
(5.4)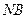 легко установить, если ввести число частиц в единице объема, т.е. концентрацию частиц (плотность числа частиц):
легко установить, если ввести число частиц в единице объема, т.е. концентрацию частиц (плотность числа частиц):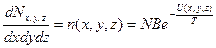 (5.5)
(5.5)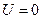 , т.е.
, т.е. 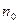 .
.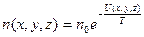 (5.6)
(5.6)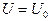 , тогда распределение Больцмана имеет вид:
, тогда распределение Больцмана имеет вид: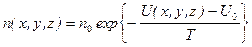 (5.7)
(5.7) ).
). (
( ), где
), где  радиус Земли. Воспользуемся малостью
радиус Земли. Воспользуемся малостью 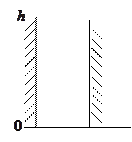
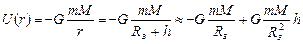 ,
,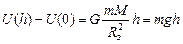
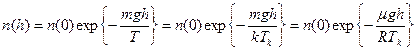 (5.8)
(5.8)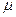 - молярная масса газа,
- молярная масса газа, 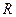 - универсальная газовая постоянная.
- универсальная газовая постоянная.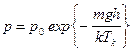 (5.9)
(5.9)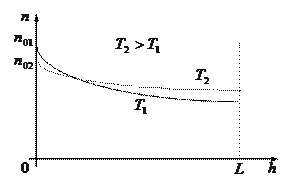
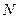 в ограниченном объеме постоянно:
в ограниченном объеме постоянно: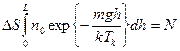 .
.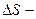 площадь сечения “сосуда”, а
площадь сечения “сосуда”, а 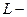 его полная высота.
его полная высота.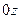 с постоянной угловой скоростью
с постоянной угловой скоростью 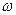 . Найдем распределение молекул в сосуде вдоль оси
. Найдем распределение молекул в сосуде вдоль оси 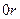 (в горизонтальной плоскости).
(в горизонтальной плоскости).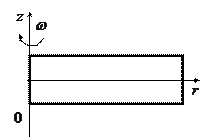 В НИСО на частицы действует центробежная сила инерции
В НИСО на частицы действует центробежная сила инерции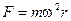 ,
, 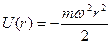 .
.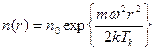 (5.10)
(5.10)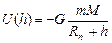
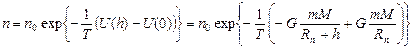 .
. мы бы получили
мы бы получили ,
, , т.е. атмосфера не должна быть в равновесии.
, т.е. атмосфера не должна быть в равновесии.


