Общие положения. Метод простой итерации
Как известно, в итерационных методах строится бесконечно повторяющийся процесс и если этот процесс сходится, то на каждом его шаге получают все более и более точное приближение к искомому решению данной системы уравнений.
Перепишем систему (4.1) в следующем виде:
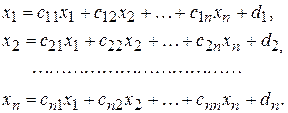 (4.29)
(4.29)
или сокращенно:
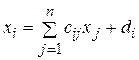 , (i = 1, 2, …, n). (4.30)
, (i = 1, 2, …, n). (4.30)
Используя систему (4.29) и выбрав начальную точку (за начальное приближение часто берут столбец свободных членов системы (4.29))
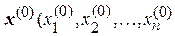 ), (4.31)
), (4.31)
можно построить итерационную последовательность точек n -мерного пространства (аналогично методу простой итерации для скалярного уравнения 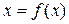 ):
):
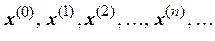 (4.32)
(4.32)
Оказывается, при определенных условиях последовательность (4.32) сходится и ее предел является решением системы (4.29), а именно, чтобы последовательность (4.32) была сходящейся, достаточно выполнения одного из названных ниже условий (выводятся на основе понятия метрическое пространство).
а) максимальная из сумм модулей коэффициентов при неизвестных в правой системы (4.29), взятых по строкам, должна быть меньше единицы:
 . (4.33)
. (4.33)
б) максимальная из сумм модулей коэффициентов при неизвестных в правой системы (4.29), взятых по столбцам, должна быть меньше единицы:
 ; (4.34)
; (4.34)
заметим, возвращаясь к системе (4.1), данное условие записывают и так:
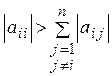 . (4.35)
. (4.35)
в) сумма квадратов всех коэффициентов при неизвестных в правой системы (4.29) должна быть меньше единицы:
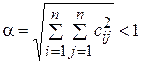 . (4.36)
. (4.36)
Необходимо отметить, что каждое из условий (4.33) – (4.36) является достаточным для того, чтобы итерационный процесс (4.32) был сходящимся, а условие (4.34) (или (4.35)) является также и необходимым.
В случае, если, допустим, условие (4.35) не выполняется, то выбирают из уравнений системы такие уравнения, модули коэффициентов в которых больше суммы модулей остальных коэффициентов. Выбранные уравнения записывают так, чтобы наибольший по модулю коэффициент оказался диагональным. Остальные уравнения составляют с помощью линейной комбинации оставшихся и выбранных уравнений.
Пример 4.1. Для системы уравнений
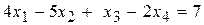 ; (a)
; (a)
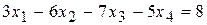 ; (b)
; (b)
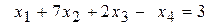 ; (c)
; (c)
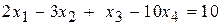 (d)
(d)
условие (4.35) выполняется только для (d): 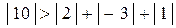 =6.
=6.
Преобразовать эту системе можно так.
Уравнение (с) нужно сделать вторым, так как в этом случае элемент, равный 7, станет диагональным и для него будет выполняться условие (4.35): 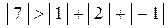 =4. Первое уравнение получаем линейной комбинацией всех четырех уравнений: 2·c + b + + a +d, а третье – как (a) – (b).
=4. Первое уравнение получаем линейной комбинацией всех четырех уравнений: 2·c + b + + a +d, а третье – как (a) – (b).
В итоге получаем систему уравнений
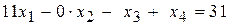 ,
,
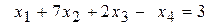 ,
,
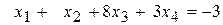 ,
,
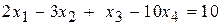 ,
,
у которой все диагональные элементы удовлетворяют условию (4.35).
Алгоритм метода простой итерации
1. Задаем >0 – точность результатов.
2. Систему (4.1) преобразуем в систему (4.29) так, чтобы выполнялись условия (4.33) – (4.36).
3. Задаем начальное приближение 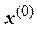 .
.
4. Подставив 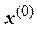 в систему (4.29), вычисляем первое приближение корня
в систему (4.29), вычисляем первое приближение корня 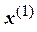 , далее, подставив
, далее, подставив 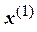 в (4.29), вычисляем
в (4.29), вычисляем 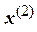 и т.д.
и т.д.
5. При достижении на некотором шаге 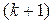 условия
условия 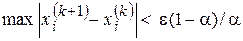 (где
(где 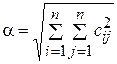 ) прекращаем счет и за решение принимаем значение
) прекращаем счет и за решение принимаем значение 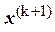 .
.
Метод Зейделя
Метод Зейделя является одним из широко применяемых итерационных методов. Выше отмечалось, что прежде чем приступить к решению системы линейных уравнений методом итераций, необходимо проверить систему на сходимость. Но для метода Зейделя разработана практическая процедура преобразования исходной системы (4.1), гарантирующей сходимость итерационного процесса, содержание которой заключается в следующем.
Представим систему (4.1) в матричной форме:
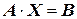 . (4.37)
. (4.37)
Умножим левую и правую части системы (4.37) слева на 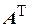 :
:
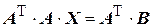 . (4.38)
. (4.38)
Обозначим в (4.38)  , а
, а 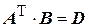 , таким образом:
, таким образом:
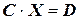 (4.39)
(4.39)
Систему (4.39) принято называть нормальной, для которой существует теорема: итерационный процесс Зейделя для системы (4.39) всегда сходится к единственному решению при любом выборе начального приближения.
Нормальную систему необходимо привести виду (4.35), допускающему осуществление итерационного процесса.
Задаем начальное приближение корня 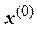 и начинаем счет.
и начинаем счет.
Основная идея метода Зейделя состоим в том, что на каждом шаге итерационного процесса 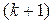 при вычислении значения
при вычислении значения 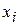 учитываются уже полученные значения
учитываются уже полученные значения 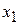 ,
, 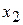 ,...,
,...,  :
:
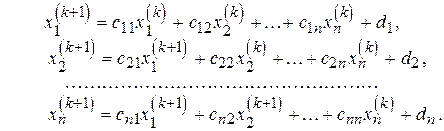 (4.40)
(4.40)
И если задана допустимая погрешность вычисления 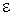 , то условием выхода из итерационного процесса будет выполнение неравенства
, то условием выхода из итерационного процесса будет выполнение неравенства 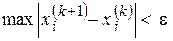 (i = 1, 2,..., n).
(i = 1, 2,..., n).



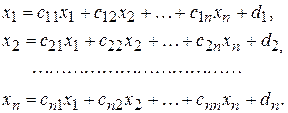 (4.29)
(4.29)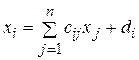 , (i = 1, 2, …, n). (4.30)
, (i = 1, 2, …, n). (4.30)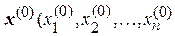 ), (4.31)
), (4.31)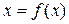 ):
):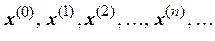 (4.32)
(4.32) . (4.33)
. (4.33) ; (4.34)
; (4.34)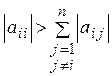 . (4.35)
. (4.35)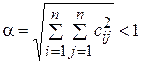 . (4.36)
. (4.36)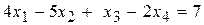 ; (a)
; (a)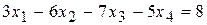 ; (b)
; (b)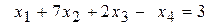 ; (c)
; (c)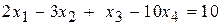 (d)
(d)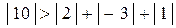 =6.
=6.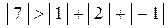 =4. Первое уравнение получаем линейной комбинацией всех четырех уравнений: 2·c + b + + a +d, а третье – как (a) – (b).
=4. Первое уравнение получаем линейной комбинацией всех четырех уравнений: 2·c + b + + a +d, а третье – как (a) – (b).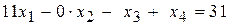 ,
,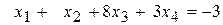 ,
,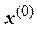 .
.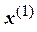 , далее, подставив
, далее, подставив 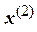 и т.д.
и т.д.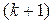 условия
условия 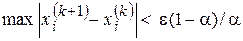 (где
(где 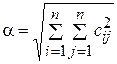 ) прекращаем счет и за решение принимаем значение
) прекращаем счет и за решение принимаем значение 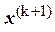 .
.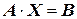 . (4.37)
. (4.37)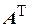 :
: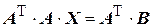 . (4.38)
. (4.38) , а
, а 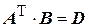 , таким образом:
, таким образом: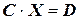 (4.39)
(4.39)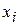 учитываются уже полученные значения
учитываются уже полученные значения 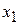 ,
, 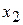 ,...,
,...,  :
: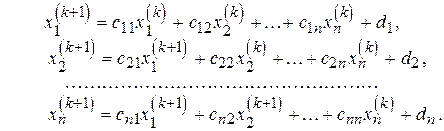 (4.40)
(4.40)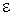 , то условием выхода из итерационного процесса будет выполнение неравенства
, то условием выхода из итерационного процесса будет выполнение неравенства 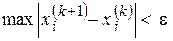 (i = 1, 2,..., n).
(i = 1, 2,..., n).


