Лабораторная работа
Изучение гармонических колебаний
Цель работы: определить массу неизвестного груза с помощью пружинного маятника; пользуясь маятником, определить величину ускорения свободного падения.
Принадлежности: пружина, набор грузов, стальной шарик на нити, штатив, фиксатор нити, секундомер, штангенциркуль, металлическая линейка.
Колебания
Колебаниями называются процессы, в той или иной степени повторяющиеся во времени.
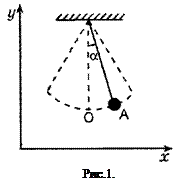 Если мы говорим, что система колеблется, то под этим подразумевается, что некоторая физическая величина, характеризующая систему, совершает колебания, т. е. изменяется, неоднократно принимая одно и то же значение. При колебаниях математического маятника (рис. 1) колеблющимися физическими величинами будут угол отклонения нити от вертикали α, координаты маятника x и y, расстояние вдоль траектории (по дуге окружности) от т. А до т. О и т. д. Когда верхушка дерева качается под действием ветра, то колеблются координаты верхушки. При распространении звука в воздухе колеблется давление воздуха в каждой точке воздушной среды. При дыхании человека колеблющейся физической величиной может служить объем грудной клетки. В колебательном контуре совершают колебания заряд конденсатора, напряжение на конденсаторе, ток в контуре и т. д. Напряжение на горящей лампочке в квартире и ток через нее тоже колеблются. Такие физические величины, как давление и температура, характеризующие состояние атмосферы, в течение, скажем, месяца, неоднократно принимают одни и те же значения, т. е. совершают колебания.
Если мы говорим, что система колеблется, то под этим подразумевается, что некоторая физическая величина, характеризующая систему, совершает колебания, т. е. изменяется, неоднократно принимая одно и то же значение. При колебаниях математического маятника (рис. 1) колеблющимися физическими величинами будут угол отклонения нити от вертикали α, координаты маятника x и y, расстояние вдоль траектории (по дуге окружности) от т. А до т. О и т. д. Когда верхушка дерева качается под действием ветра, то колеблются координаты верхушки. При распространении звука в воздухе колеблется давление воздуха в каждой точке воздушной среды. При дыхании человека колеблющейся физической величиной может служить объем грудной клетки. В колебательном контуре совершают колебания заряд конденсатора, напряжение на конденсаторе, ток в контуре и т. д. Напряжение на горящей лампочке в квартире и ток через нее тоже колеблются. Такие физические величины, как давление и температура, характеризующие состояние атмосферы, в течение, скажем, месяца, неоднократно принимают одни и те же значения, т. е. совершают колебания.
Колебательные процессы встречаются в разнообразных физических явлениях и широко распространены в окружающем нас мире. Несмотря на то, что колебания могут иметь различную физическую природу, они часто подчиняются одним итем же закономерностям, описываются одинаковыми математическими формулами и уравнениями. Это позволяет с единой точки зрения математически описать отличающиеся по физической природе колебания.
Периодические колебания
Колебания некоторой физической величины S называются периодическими, если все значения этой величины полностью повторяются через одно и то же время Τ, называемое периодом, т. е. S (t + Τ) = S (t) для любого значения времени t. Если Τ – период, то 2Т, 3Т, 4Τ,... тоже периоды. Поэтому в физике под периодом обычно понимают наименьший период, т. е. наименьший отрезок времени, через который физическая величина S повторяется. При этом говорят, что за время одного периода совершается одно колебание.
Частотой периодических колебаний ν называется число колебаний в единицу времени. Легко показать, что
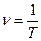 .
.
Действительно, если за время t совершено N колебаний, то частота 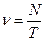 , а период
, а период 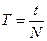 . Отсюда видно, что
. Отсюда видно, что 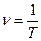 . В системе СИ единицей измерения частоты служит Герц (Гц), 1 Гц = с -1.
. В системе СИ единицей измерения частоты служит Герц (Гц), 1 Гц = с -1.
Пусть периодически колеблющаяся величина S изменяется в пределах от S 0– А до S 0+ А, где А > 0. Тогда говорят, что величина S колеблется с амплитудой А около значения S 0. Размах колебаний (разница между двумя крайними положениями) равен 2А.
Гармонические колебания
Важным частным случаем периодических колебаний являются гармонические колебания, т. е. такие изменения во времени t физической величины S, которые идут по закону
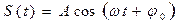 , (1)
, (1)
где А > 0, ω > 0. Из курса математики известно, что функция вида (1) меняется в пределах от – А до А, и что наименьший положительный период у нее 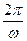 . Поэтому гармоническое колебание вида (1) происходит с амплитудой А и периодом
. Поэтому гармоническое колебание вида (1) происходит с амплитудой А и периодом 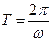 .
.
Не следует путать циклическую (круговую) частоту ω ичастоту ν колебаний.
Между ними простая связь. Так как 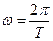 и
и 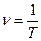 , то
, то
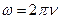 .
.
В системе СИ размерность как ω, таки ν равна с-1. Наименование Гц обычно применяется только для величины ν, а если необходимо указать размерность ω, то пишут просто с-1.
Величина 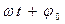 называется фазой колебаний. Фаза растет пропорционально времени. При t = 0 фаза равна
называется фазой колебаний. Фаза растет пропорционально времени. При t = 0 фаза равна 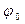 , и поэтому
, и поэтому 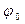 называется начальной фазой. Она зависит от отклонения и скорости в момент начала отсчета времени.
называется начальной фазой. Она зависит от отклонения и скорости в момент начала отсчета времени.
Отметим, что при одном и том же t: 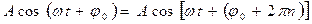 , где n=0, ±1, ±2, … Видно, что начальная фаза для одного и того же колебания есть величина, определенная с точностью до 2 π n. Поэтому из множества возможных значений начальной фазы выбирают обычно значение начальной фазы наименьшее по модулю или наименьшее положительное. Но делать это не обязательно. Например, если дано колебание
, где n=0, ±1, ±2, … Видно, что начальная фаза для одного и того же колебания есть величина, определенная с точностью до 2 π n. Поэтому из множества возможных значений начальной фазы выбирают обычно значение начальной фазы наименьшее по модулю или наименьшее положительное. Но делать это не обязательно. Например, если дано колебание 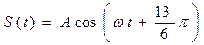 , то удобнее записать его в виде
, то удобнее записать его в виде 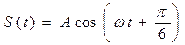 и работать в дальнейшем с последним видом записи этого колебания.
и работать в дальнейшем с последним видом записи этого колебания.
Можно показать, что колебания вида
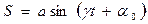 и
и 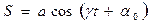 , (2)
, (2)
где а и γмогут быть любого знака, с помощью простых тригонометрических преобразований всегда приводятся к виду (1), причем А = |а|, ω = | γ |, а 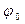 не равно
не равно 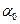 вообще говоря. Таким образом, колебания вида (2) являются гармоническими, с амплитудой |а| и циклической частотой | γ |. Не приводя общего доказательства, проиллюстрируем это на конкретном примере.
вообще говоря. Таким образом, колебания вида (2) являются гармоническими, с амплитудой |а| и циклической частотой | γ |. Не приводя общего доказательства, проиллюстрируем это на конкретном примере.
Пусть требуется показать, что колебание 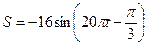 будет гармоническим, и найти амплитуду А, циклическую частоту ω, период Τ и начальную фазу
будет гармоническим, и найти амплитуду А, циклическую частоту ω, период Τ и начальную фазу 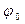 .
.
Действительно, 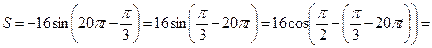
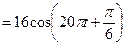 . Видим, что колебание величины S удалось записать в форме (1). При этом А = 16, ω = 20π,
. Видим, что колебание величины S удалось записать в форме (1). При этом А = 16, ω = 20π, 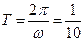 ,
, 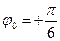 .
.
Попробуйте самостоятельно убедиться, что
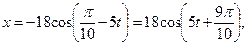
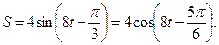
Естественно, что запись гармонических колебаний в форме (2) ничем не хуже записи в форме (1), и переходить в конкретной задаче от записи в одной форме к записи в другой обычно нет необходимости. Нужно только уметь сразу находить амплитуду, циклическую частоту ипериод, имея перед собой любую форму записи гармонического колебания.
Иногда полезно знать характер изменения первой и второй производных по времени от величины S, которая совершает гармонические колебания (колебания по гармоническому закону). Если 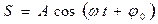 , то дифференцирование S по времени t дает
, то дифференцирование S по времени t дает
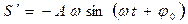 ,
, 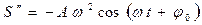 .
.
Пример. Координата x тела, совершающего гармонические колебания вдоль оси x, изменяется по закону x = 2 sin 6 t, где x – в сантиметрах, время t – в секундах. Требуется записать закон изменения скорости и ускорения тела и найти их максимальное значение. Для ответа на поставленный вопрос, заметим, что первая производная по времени от величины x есть проекция скорости тела на ось x, а вторая производная от x есть проекция ускорения на ось x: 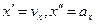 . Продифференцировав выражения для x по времени, получаем:
. Продифференцировав выражения для x по времени, получаем: 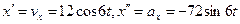 .Максимальные значения скорости и ускорения v max = 12 см/с, а max = 72 см/с2.
.Максимальные значения скорости и ускорения v max = 12 см/с, а max = 72 см/с2.
Пружинный маятник
Пусть на гладком горизонтальном столе груз массой m совершает колебания вдоль оси x на легкой пружине жесткости k (рис. 5), прикрепленной одним концом к грузу, а другим к стене. Покажем, что свободные колебания такого пружинного маятника гармонические и найдем их период.
Начало координат (x = 0) поместим в точку, соответствующую равновесному положению груза. За колеблющуюся физическую величину возьмем координату груза.
1-й способ решения. Используется второй закон Ньютона.
Пусть груз при колебаниях в некоторый момент времени t имеет координату x = x (t). Тогда проекция на ось x силы 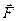 , действующей на груз со стороны пружины,
, действующей на груз со стороны пружины,
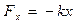 (4)
(4)
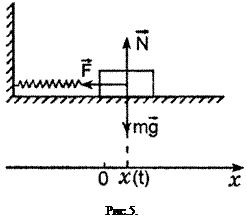 при любом знаке x, что легко проверить. На рис. 5 покачано направление силы
при любом знаке x, что легко проверить. На рис. 5 покачано направление силы 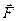 при x > 0. На груз еще действует сила тяжести
при x > 0. На груз еще действует сила тяжести 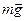 и сила нормального давления
и сила нормального давления 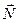 со стороны стола. По второму закону Ньютона
со стороны стола. По второму закону Ньютона 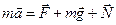 , где
, где 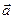 – ускорение груза.
– ускорение груза.
Это векторное равенство, записанное в проекциях на ось x, имеет вид max = Fx. Здесь ах = х " – проекция на ось x ускорения. Учитывая (4), имеем т х " = - k х. Отсюда
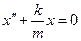 .
.
Последнее уравнение есть дифференциальное уравнение гармонических колебаний с циклической частотой 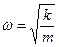 и периодом
и периодом 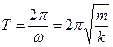 .
.
2-й способ. Используется закон сохранения энергии.
В момент, когда груз имеет координату x и проекцию на ось x скорости x ', кинетическая энергия груза будет 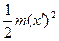 , а потенциальная энергия деформированной пружины
, а потенциальная энергия деформированной пружины 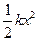 . Так как полная энергия системы при колебаниях сохраняется, то
. Так как полная энергия системы при колебаниях сохраняется, то 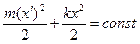 . Продифференцируем последнее равенство по времени:
. Продифференцируем последнее равенство по времени: 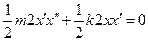 . Откуда
. Откуда 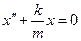 .
.
Как и в первом способе решения, но уже другим путем, мы получили дифференциальное уравнение гармонических колебаний с циклической частотой 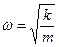 и периодом
и периодом 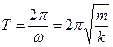 .
.
Главной особенностью движения рассмотренного маятника является независимость амплитуды колебаний от частоты. Это справедливо при небольшой амплитуде, когда величина деформации пружины пропорциональна силе, действующей на пружину (см.(4)). При большой амплитуде колебаний это условие нарушается, и частота колебаний начинает зависеть от амплитуды.
Уравнение колебаний пружинного маятника:
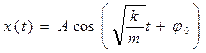 . (5)
. (5)
Амплитуду колебаний А и начальную фазу φ0 можно определить, зная положение груза x 0 и его скорость v 0 в некоторый момент времени, например, t = 0.
Продифференцируем уравнение (5) по времени:
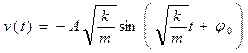 . (6)
. (6)
Подставив в (5) и (6) значения координаты и скорости груза при t =0, получим систему уравнений
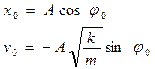 , (7)
, (7)
из которой легко найти А и φ0:
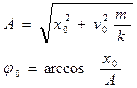 .
.
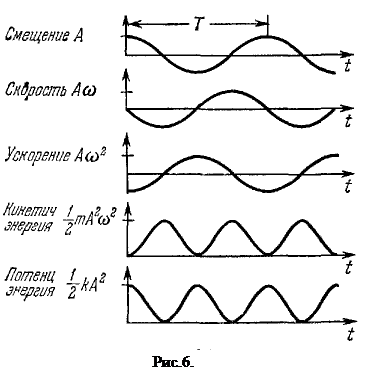 При гармонических колебаниях полная энергия остается постоянной, но кинетическая и потенциальная, каждая в отдельности, совершают колебания во времени. В момент, когда колеблющееся тело достигает крайнего положения и имеет скорость, равную нулю, вся энергия является потенциальной – кинетическая равна нулю. Когда тело проходит через положение равновесия, вся энергия является кинетической – потенциальная равна нулю (если в положении равновесия потенциальная энергия равна нулю). Поскольку тело за период колебаний два раза проходит через положение равновесия, то частота колебаний кинетической энергии в два раза больше частоты колебаний груза. С таким же периодом колеблется и потенциальная энергия.
При гармонических колебаниях полная энергия остается постоянной, но кинетическая и потенциальная, каждая в отдельности, совершают колебания во времени. В момент, когда колеблющееся тело достигает крайнего положения и имеет скорость, равную нулю, вся энергия является потенциальной – кинетическая равна нулю. Когда тело проходит через положение равновесия, вся энергия является кинетической – потенциальная равна нулю (если в положении равновесия потенциальная энергия равна нулю). Поскольку тело за период колебаний два раза проходит через положение равновесия, то частота колебаний кинетической энергии в два раза больше частоты колебаний груза. С таким же периодом колеблется и потенциальная энергия.
На рис.6 показан ход изменения со временем величин, характеризующих движение маятника.
Если в некоторой системе, не обязательно состоящей из груза и пружины, возвращающая сила пропорциональна отклонению от положения равновесия, то такая система становится подобной пружинному маятнику, и в ней могут возникнуть гармонические колебания.
Лабораторная работа
Изучение гармонических колебаний
Цель работы: определить массу неизвестного груза с помощью пружинного маятника; пользуясь маятником, определить величину ускорения свободного падения.
Принадлежности: пружина, набор грузов, стальной шарик на нити, штатив, фиксатор нити, секундомер, штангенциркуль, металлическая линейка.
Колебания
Колебаниями называются процессы, в той или иной степени повторяющиеся во времени.
 Если мы говорим, что система колеблется, то под этим подразумевается, что некоторая физическая величина, характеризующая систему, совершает колебания, т. е. изменяется, неоднократно принимая одно и то же значение. При колебаниях математического маятника (рис. 1) колеблющимися физическими величинами будут угол отклонения нити от вертикали α, координаты маятника x и y, расстояние вдоль траектории (по дуге окружности) от т. А до т. О и т. д. Когда верхушка дерева качается под действием ветра, то колеблются координаты верхушки. При распространении звука в воздухе колеблется давление воздуха в каждой точке воздушной среды. При дыхании человека колеблющейся физической величиной может служить объем грудной клетки. В колебательном контуре совершают колебания заряд конденсатора, напряжение на конденсаторе, ток в контуре и т. д. Напряжение на горящей лампочке в квартире и ток через нее тоже колеблются. Такие физические величины, как давление и температура, характеризующие состояние атмосферы, в течение, скажем, месяца, неоднократно принимают одни и те же значения, т. е. совершают колебания.
Если мы говорим, что система колеблется, то под этим подразумевается, что некоторая физическая величина, характеризующая систему, совершает колебания, т. е. изменяется, неоднократно принимая одно и то же значение. При колебаниях математического маятника (рис. 1) колеблющимися физическими величинами будут угол отклонения нити от вертикали α, координаты маятника x и y, расстояние вдоль траектории (по дуге окружности) от т. А до т. О и т. д. Когда верхушка дерева качается под действием ветра, то колеблются координаты верхушки. При распространении звука в воздухе колеблется давление воздуха в каждой точке воздушной среды. При дыхании человека колеблющейся физической величиной может служить объем грудной клетки. В колебательном контуре совершают колебания заряд конденсатора, напряжение на конденсаторе, ток в контуре и т. д. Напряжение на горящей лампочке в квартире и ток через нее тоже колеблются. Такие физические величины, как давление и температура, характеризующие состояние атмосферы, в течение, скажем, месяца, неоднократно принимают одни и те же значения, т. е. совершают колебания.
Колебательные процессы встречаются в разнообразных физических явлениях и широко распространены в окружающем нас мире. Несмотря на то, что колебания могут иметь различную физическую природу, они часто подчиняются одним итем же закономерностям, описываются одинаковыми математическими формулами и уравнениями. Это позволяет с единой точки зрения математически описать отличающиеся по физической природе колебания.
Периодические колебания
Колебания некоторой физической величины S называются периодическими, если все значения этой величины полностью повторяются через одно и то же время Τ, называемое периодом, т. е. S (t + Τ) = S (t) для любого значения времени t. Если Τ – период, то 2Т, 3Т, 4Τ,... тоже периоды. Поэтому в физике под периодом обычно понимают наименьший период, т. е. наименьший отрезок времени, через который физическая величина S повторяется. При этом говорят, что за время одного периода совершается одно колебание.
Частотой периодических колебаний ν называется число колебаний в единицу времени. Легко показать, что
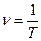 .
.
Действительно, если за время t совершено N колебаний, то частота 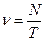 , а период
, а период 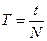 . Отсюда видно, что
. Отсюда видно, что 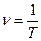 . В системе СИ единицей измерения частоты служит Герц (Гц), 1 Гц = с -1.
. В системе СИ единицей измерения частоты служит Герц (Гц), 1 Гц = с -1.
Пусть периодически колеблющаяся величина S изменяется в пределах от S 0– А до S 0+ А, где А > 0. Тогда говорят, что величина S колеблется с амплитудой А около значения S 0. Размах колебаний (разница между двумя крайними положениями) равен 2А.
Гармонические колебания
Важным частным случаем периодических колебаний являются гармонические колебания, т. е. такие изменения во времени t физической величины S, которые идут по закону
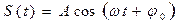 , (1)
, (1)
где А > 0, ω > 0. Из курса математики известно, что функция вида (1) меняется в пределах от – А до А, и что наименьший положительный период у нее 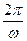 . Поэтому гармоническое колебание вида (1) происходит с амплитудой А и периодом
. Поэтому гармоническое колебание вида (1) происходит с амплитудой А и периодом 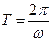 .
.
Не следует путать циклическую (круговую) частоту ω ичастоту ν колебаний.
Между ними простая связь. Так как 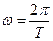 и
и 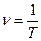 , то
, то
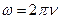 .
.
В системе СИ размерность как ω, таки ν равна с-1. Наименование Гц обычно применяется только для величины ν, а если необходимо указать размерность ω, то пишут просто с-1.
Величина 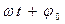 называется фазой колебаний. Фаза растет пропорционально времени. При t = 0 фаза равна
называется фазой колебаний. Фаза растет пропорционально времени. При t = 0 фаза равна 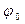 , и поэтому
, и поэтому 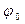 называется начальной фазой. Она зависит от отклонения и скорости в момент начала отсчета времени.
называется начальной фазой. Она зависит от отклонения и скорости в момент начала отсчета времени.
Отметим, что при одном и том же t: 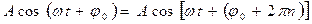 , где n=0, ±1, ±2, … Видно, что начальная фаза для одного и того же колебания есть величина, определенная с точностью до 2 π n. Поэтому из множества возможных значений начальной фазы выбирают обычно значение начальной фазы наименьшее по модулю или наименьшее положительное. Но делать это не обязательно. Например, если дано колебание
, где n=0, ±1, ±2, … Видно, что начальная фаза для одного и того же колебания есть величина, определенная с точностью до 2 π n. Поэтому из множества возможных значений начальной фазы выбирают обычно значение начальной фазы наименьшее по модулю или наименьшее положительное. Но делать это не обязательно. Например, если дано колебание 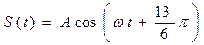 , то удобнее записать его в виде
, то удобнее записать его в виде 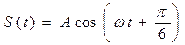 и работать в дальнейшем с последним видом записи этого колебания.
и работать в дальнейшем с последним видом записи этого колебания.
Можно показать, что колебания вида
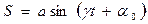 и
и 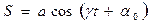 , (2)
, (2)
где а и γмогут быть любого знака, с помощью простых тригонометрических преобразований всегда приводятся к виду (1), причем А = |а|, ω = | γ |, а 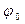 не равно
не равно 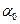 вообще говоря. Таким образом, колебания вида (2) являются гармоническими, с амплитудой |а| и циклической частотой | γ |. Не приводя общего доказательства, проиллюстрируем это на конкретном примере.
вообще говоря. Таким образом, колебания вида (2) являются гармоническими, с амплитудой |а| и циклической частотой | γ |. Не приводя общего доказательства, проиллюстрируем это на конкретном примере.
Пусть требуется показать, что колебание 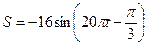 будет гармоническим, и найти амплитуду А, циклическую частоту ω, период Τ и начальную фазу
будет гармоническим, и найти амплитуду А, циклическую частоту ω, период Τ и начальную фазу 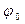 .
.
Действительно, 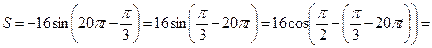
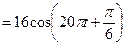 . Видим, что колебание величины S удалось записать в форме (1). При этом А = 16, ω = 20π,
. Видим, что колебание величины S удалось записать в форме (1). При этом А = 16, ω = 20π, 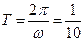 ,
, 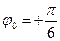 .
.
Попробуйте самостоятельно убедиться, что
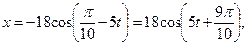
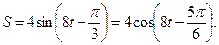
Естественно, что запись гармонических колебаний в форме (2) ничем не хуже записи в форме (1), и переходить в конкретной задаче от записи в одной форме к записи в другой обычно нет необходимости. Нужно только уметь сразу находить амплитуду, циклическую частоту ипериод, имея перед собой любую форму записи гармонического колебания.
Иногда полезно знать характер изменения первой и второй производных по времени от величины S, которая совершает гармонические колебания (колебания по гармоническому закону). Если 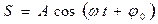 , то дифференцирование S по времени t дает
, то дифференцирование S по времени t дает
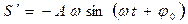 ,
, 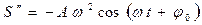 .
.
Пример. Координата x тела, совершающего гармонические колебания вдоль оси x, изменяется по закону x = 2 sin 6 t, где x – в сантиметрах, время t – в секундах. Требуется записать закон изменения скорости и ускорения тела и найти их максимальное значение. Для ответа на поставленный вопрос, заметим, что первая производная по времени от величины x есть проекция скорости тела на ось x, а вторая производная от x есть проекция ускорения на ось x: 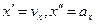 . Продифференцировав выражения для x по времени, получаем:
. Продифференцировав выражения для x по времени, получаем: 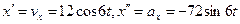 .Максимальные значения скорости и ускорения v max = 12 см/с, а max = 72 см/с2.
.Максимальные значения скорости и ускорения v max = 12 см/с, а max = 72 см/с2.
Дифференциальное уравнение гармонических колебаний
Пусть некоторая физическая величина S совершает гармонические колебания (1). Легко показать, что вторая производная по времен от S равна 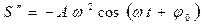 . С учетом (1) получаем, что
. С учетом (1) получаем, что  , т.е.
, т.е.
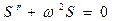 . (3)
. (3)
Итак, можно сделать вывод: если величина S изменяется по гармоническому закону (1), то отсюда следует справедливость равенства (3). В математике показывается и обратное: если для величины S = S (t) справедливо равенство (3) при всех допустимых значениях t, то S (t) имеет только вид (1) и никакой другой. Причем А и 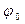 в (1) есть произвольные постоянные, конкретные значения которых зависят от так называемых начальных условий, т. е. от значений S и ее производной S ' в некоторый момент времени t (обычно при t = 0 ).
в (1) есть произвольные постоянные, конкретные значения которых зависят от так называемых начальных условий, т. е. от значений S и ее производной S ' в некоторый момент времени t (обычно при t = 0 ).
Равенство (3) называют дифференциальным уравнением гармонических колебаний.
Таким образом, мы получили чрезвычайно важное утверждение:
если с помощью законов физики для физической величины S удалось записать дифференциальное уравнение вида 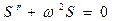 , то отсюда будет следовать, что S изменяется обязательно, по гармоническому закону
, то отсюда будет следовать, что S изменяется обязательно, по гармоническому закону 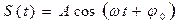 с циклической частотой
с циклической частотой 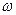 (
(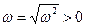 ). Конкретные значения амплитуды А и начальной фазы
). Конкретные значения амплитуды А и начальной фазы 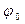 зависят от начальных условий.
зависят от начальных условий.
Заметим, что в (3) стоит величина 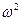 , которая всегда положительна. Поэтому, например, уравнение
, которая всегда положительна. Поэтому, например, уравнение 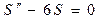 не будет дифференциальным уравнением гармонических колебаний, т.к. не найдется такого действительного значения
не будет дифференциальным уравнением гармонических колебаний, т.к. не найдется такого действительного значения 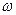 , для которого
, для которого 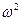 было бы равно «– 6».
было бы равно «– 6».



 Если мы говорим, что система колеблется, то под этим подразумевается, что некоторая физическая величина, характеризующая систему, совершает колебания, т. е. изменяется, неоднократно принимая одно и то же значение. При колебаниях математического маятника (рис. 1) колеблющимися физическими величинами будут угол отклонения нити от вертикали α, координаты маятника x и y, расстояние вдоль траектории (по дуге окружности) от т. А до т. О и т. д. Когда верхушка дерева качается под действием ветра, то колеблются координаты верхушки. При распространении звука в воздухе колеблется давление воздуха в каждой точке воздушной среды. При дыхании человека колеблющейся физической величиной может служить объем грудной клетки. В колебательном контуре совершают колебания заряд конденсатора, напряжение на конденсаторе, ток в контуре и т. д. Напряжение на горящей лампочке в квартире и ток через нее тоже колеблются. Такие физические величины, как давление и температура, характеризующие состояние атмосферы, в течение, скажем, месяца, неоднократно принимают одни и те же значения, т. е. совершают колебания.
Если мы говорим, что система колеблется, то под этим подразумевается, что некоторая физическая величина, характеризующая систему, совершает колебания, т. е. изменяется, неоднократно принимая одно и то же значение. При колебаниях математического маятника (рис. 1) колеблющимися физическими величинами будут угол отклонения нити от вертикали α, координаты маятника x и y, расстояние вдоль траектории (по дуге окружности) от т. А до т. О и т. д. Когда верхушка дерева качается под действием ветра, то колеблются координаты верхушки. При распространении звука в воздухе колеблется давление воздуха в каждой точке воздушной среды. При дыхании человека колеблющейся физической величиной может служить объем грудной клетки. В колебательном контуре совершают колебания заряд конденсатора, напряжение на конденсаторе, ток в контуре и т. д. Напряжение на горящей лампочке в квартире и ток через нее тоже колеблются. Такие физические величины, как давление и температура, характеризующие состояние атмосферы, в течение, скажем, месяца, неоднократно принимают одни и те же значения, т. е. совершают колебания.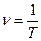 .
.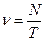 , а период
, а период 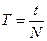 . Отсюда видно, что
. Отсюда видно, что 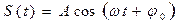 , (1)
, (1)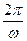 . Поэтому гармоническое колебание вида (1) происходит с амплитудой А и периодом
. Поэтому гармоническое колебание вида (1) происходит с амплитудой А и периодом 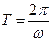 .
.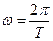 и
и 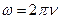 .
.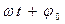 называется фазой колебаний. Фаза растет пропорционально времени. При t = 0 фаза равна
называется фазой колебаний. Фаза растет пропорционально времени. При t = 0 фаза равна 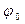 , и поэтому
, и поэтому 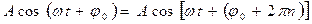 , где n=0, ±1, ±2, … Видно, что начальная фаза для одного и того же колебания есть величина, определенная с точностью до 2 π n. Поэтому из множества возможных значений начальной фазы выбирают обычно значение начальной фазы наименьшее по модулю или наименьшее положительное. Но делать это не обязательно. Например, если дано колебание
, где n=0, ±1, ±2, … Видно, что начальная фаза для одного и того же колебания есть величина, определенная с точностью до 2 π n. Поэтому из множества возможных значений начальной фазы выбирают обычно значение начальной фазы наименьшее по модулю или наименьшее положительное. Но делать это не обязательно. Например, если дано колебание 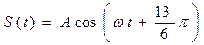 , то удобнее записать его в виде
, то удобнее записать его в виде 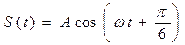 и работать в дальнейшем с последним видом записи этого колебания.
и работать в дальнейшем с последним видом записи этого колебания.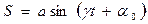 и
и 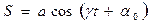 , (2)
, (2)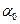 вообще говоря. Таким образом, колебания вида (2) являются гармоническими, с амплитудой |а| и циклической частотой | γ |. Не приводя общего доказательства, проиллюстрируем это на конкретном примере.
вообще говоря. Таким образом, колебания вида (2) являются гармоническими, с амплитудой |а| и циклической частотой | γ |. Не приводя общего доказательства, проиллюстрируем это на конкретном примере.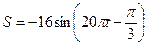 будет гармоническим, и найти амплитуду А, циклическую частоту ω, период Τ и начальную фазу
будет гармоническим, и найти амплитуду А, циклическую частоту ω, период Τ и начальную фазу 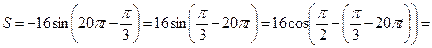
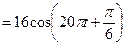 . Видим, что колебание величины S удалось записать в форме (1). При этом А = 16, ω = 20π,
. Видим, что колебание величины S удалось записать в форме (1). При этом А = 16, ω = 20π, 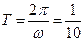 ,
, 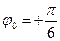 .
.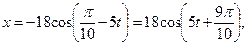
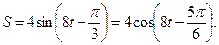
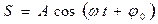 , то дифференцирование S по времени t дает
, то дифференцирование S по времени t дает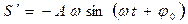 ,
, 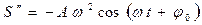 .
.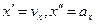 . Продифференцировав выражения для x по времени, получаем:
. Продифференцировав выражения для x по времени, получаем: 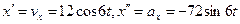 .Максимальные значения скорости и ускорения v max = 12 см/с, а max = 72 см/с2.
.Максимальные значения скорости и ускорения v max = 12 см/с, а max = 72 см/с2.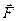 , действующей на груз со стороны пружины,
, действующей на груз со стороны пружины,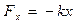 (4)
(4) при любом знаке x, что легко проверить. На рис. 5 покачано направление силы
при любом знаке x, что легко проверить. На рис. 5 покачано направление силы 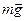 и сила нормального давления
и сила нормального давления 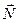 со стороны стола. По второму закону Ньютона
со стороны стола. По второму закону Ньютона 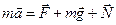 , где
, где 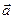 – ускорение груза.
– ускорение груза.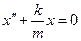 .
.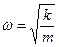 и периодом
и периодом 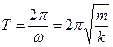 .
.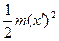 , а потенциальная энергия деформированной пружины
, а потенциальная энергия деформированной пружины 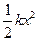 . Так как полная энергия системы при колебаниях сохраняется, то
. Так как полная энергия системы при колебаниях сохраняется, то 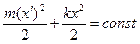 . Продифференцируем последнее равенство по времени:
. Продифференцируем последнее равенство по времени: 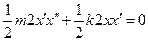 . Откуда
. Откуда 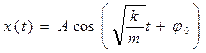 . (5)
. (5)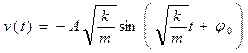 . (6)
. (6)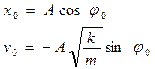 , (7)
, (7)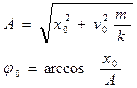 .
. При гармонических колебаниях полная энергия остается постоянной, но кинетическая и потенциальная, каждая в отдельности, совершают колебания во времени. В момент, когда колеблющееся тело достигает крайнего положения и имеет скорость, равную нулю, вся энергия является потенциальной – кинетическая равна нулю. Когда тело проходит через положение равновесия, вся энергия является кинетической – потенциальная равна нулю (если в положении равновесия потенциальная энергия равна нулю). Поскольку тело за период колебаний два раза проходит через положение равновесия, то частота колебаний кинетической энергии в два раза больше частоты колебаний груза. С таким же периодом колеблется и потенциальная энергия.
При гармонических колебаниях полная энергия остается постоянной, но кинетическая и потенциальная, каждая в отдельности, совершают колебания во времени. В момент, когда колеблющееся тело достигает крайнего положения и имеет скорость, равную нулю, вся энергия является потенциальной – кинетическая равна нулю. Когда тело проходит через положение равновесия, вся энергия является кинетической – потенциальная равна нулю (если в положении равновесия потенциальная энергия равна нулю). Поскольку тело за период колебаний два раза проходит через положение равновесия, то частота колебаний кинетической энергии в два раза больше частоты колебаний груза. С таким же периодом колеблется и потенциальная энергия.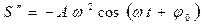 . С учетом (1) получаем, что
. С учетом (1) получаем, что  , т.е.
, т.е.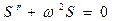 . (3)
. (3)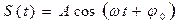 с циклической частотой
с циклической частотой 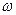 (
(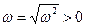 ). Конкретные значения амплитуды А и начальной фазы
). Конкретные значения амплитуды А и начальной фазы 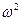 , которая всегда положительна. Поэтому, например, уравнение
, которая всегда положительна. Поэтому, например, уравнение 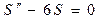 не будет дифференциальным уравнением гармонических колебаний, т.к. не найдется такого действительного значения
не будет дифференциальным уравнением гармонических колебаний, т.к. не найдется такого действительного значения 


