

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы...
Интересное:
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
§1. Криволинейные интегралы 1-го рода
1.Определение, существование
Рассмотрим спрямляемую кривую g и функцию f (x, y, z), определенную на этой кривой
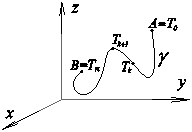
«Упорядоченный вдоль кривой» набор точек { Tk }, k =0,1,…, n называется разбиением кривой T ={ Tk }. На каждой дуге Tk Tk +1 задана промежуточная точка X k =(x k, h k, z k), X ={ X k }, обозначим длину дуги Tk Tk +1 через lk, длину хорды, стягивающей дугу Tk Tk +1 обозначим D lk. Характеристикой разбиения T назовем величину l (T) = max D lk. Составим интегральные суммы следующего вида
s (f, T, X)=  (1).
(1).
Предел сумм (1) при стремлении к нулю характеристики разбиения l (T), при условии существования этого предела и независимости его от выбора промежуточных точек, называется криволинейным интегралом 1-го рода и обозначается
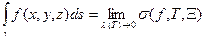 .
.
Точное определение на кванторах дается так же, как и для обычного интеграла
$ J " e >0 $ d >0:(l (T)< d, X Î T) Þ | s (f,T, X) - J|< e.
Можно использовать эквивалентное определение, беря в качестве интегральных сумм суммы вида 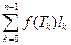 , где вместо длины хорды D lk берется длина дуги lk. Доказательство эквивалентности этих определений для гладкой кривой будет дано позже.
, где вместо длины хорды D lk берется длина дуги lk. Доказательство эквивалентности этих определений для гладкой кривой будет дано позже.
Замечание 1. Если кривая g плоская, (например, лежит в плоскости Oxy), и f = f (x, y), то интеграл обозначается 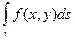 .
.
Замечание 2. Интегральная сумма не изменится, если произвести поворот или сдвиг системы координат. Это свойство называется свойством инвариантности интеграла относительно поворотов и сдвигов системы координат.
Рассмотрим случай, когда кривая задана параметрически
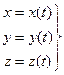 , t Î [ a, b ] (2)
, t Î [ a, b ] (2)
Теорема 1. Если кривая (2) гладкая (непрерывно дифференцируема без особых точек
(x ¢ 2 + y ¢ 2 + z ¢ 2 ¹ 0)), функция f (x, y, z) непрерывна на (2), тогда криволинейный интеграл  существует и имеет место равенство
существует и имеет место равенство
|
|
 =
= 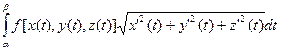 (3)
(3)
Доказательство. Для простоты будем рассматривать случай плоской кривой. Выберем разбиение { tj } отрезка [ a, b ].
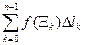 =
=  =
=  =
=  +
+ 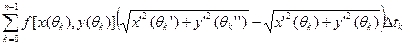 .
.
Второй интеграл в последнем равенстве можно сделать сколь угодно малым выбором достаточно мелкого разбиения. Действительно,
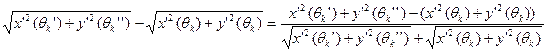 =
=  . Знаменатель этой дроби ограничен снизу (у кривой нет особых точек и вторая теорема Вейерштрасса). Числитель можно сделать малым в силу равномерной непрерывности. Таким образом, пределом сумм
. Знаменатель этой дроби ограничен снизу (у кривой нет особых точек и вторая теорема Вейерштрасса). Числитель можно сделать малым в силу равномерной непрерывности. Таким образом, пределом сумм  будет интеграл
будет интеграл
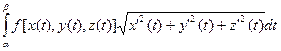 .
.
Для доказательства эквивалентности двух определений, для заданного разбиения { tj } отрезка [ a, b ] промежуточные точки x j выберем так, что
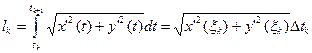 ,
,
соответствующие точки на кривой g обозначим X k =(x (x k), y (x k)). Для интегральной суммы получим
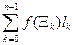 =
= 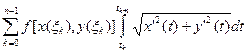 =
= 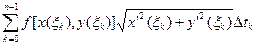
Полученная сумма является интегральной суммой для интеграла 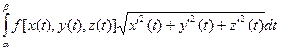 , откуда и следует требуемое утверждение.
, откуда и следует требуемое утверждение.
Замечание. Отметим, что интеграл первого рода не зависит от выбора порядка точек разбиения { Ak } (что считать началом кривой, а что концом, что в дальнейшем будет определяться, как ориентация кривой). Точки A, B могут совпадать.
2. Свойства криволинейного интеграла 1-го рода.
1) 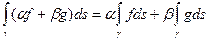
2) (Аддитивность по множеству) Если дуга AB составлена из двух дуг AC и CB и существует  , то существуют
, то существуют 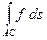 и
и  и справедлива формула
и справедлива формула
 =
= 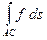 +
+ 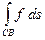
1) Если существует 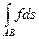 , то существует и
, то существует и 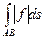 и выполнено неравенство
и выполнено неравенство  £
£ 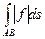 .
.
2) (Инвариантность интеграла относительно поворотов и сдвигов системы координат) При поворотах системы координат вокруг осей и при сдвигах криволинейный интеграл не меняется.
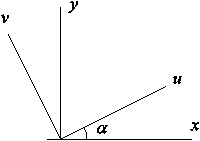
Поясним это свойство на примере отображения
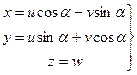
| 
|
(поворот на угол a вокруг оси Oz)
Если функция f (x, y, z) определена на g, то в системе координат (u, v, w) функция
F(u,v,w)=f(u cos a - v sin a, u sin a + v cos a, w)
Будет определена на образе G кривой g. И в данном случае это свойство означает равенство интегралов
 .
.
Доказательства свойств 1)-3) те же, что и для обычных интегралов. Для кусочно-гладкой кривой эти свойства следуют из соответствующих свойств обычного интеграла
|
|
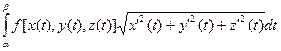 .
.
Замечание. Свойство аддитивности интеграла по множеству позволяет распространить утверждение теоремы 1 предыдущего пункта на кусочно-гладкие кривые.
§2. Криволинейные интегралы 2-го рода
1.Определение, существование.
Рассмотрим кривую g с началом в точке A и концом в точке B. Пусть T ={ Tk } разбиение кривой g и X ={ X k }, X k =(x k, h k, z k), набор промежуточных точек, D xj = xj +1 – xj.
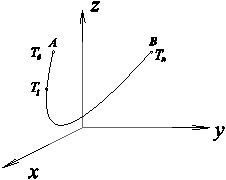
Для функции f (x, y, z), данной кривой, разбиения и набора промежуточных точекобразуем интегральные суммы
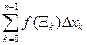 (1)
(1)
Предел сумм (1) при l (T) ® 0, если он не зависит от выбора разбиений и промежуточных точек, называется криволинейным интегралом 2-го рода и обозначается
 (2)
(2)
Характеристика разбиения определяется так же, как для интеграла первого рода l (T) = max D lk. Аналогично можно определить интегралы
 ,
,  .
.
Замечание 1. Если началом кривой выбрать точку B, то все 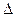 xj меняют знак, поэтому
xj меняют знак, поэтому
 =
=  .
.
Замечание 2. Интегральная сумма не изменится, если произвести поворот или сдвиг системы координат. Это свойство называется свойством инвариантности интеграла относительно поворотов и сдвигов системы координат.
Теорема 1. Пусть кривая g задана в параметрическом виде
 , t Î [ a, b ] (3)
, t Î [ a, b ] (3)
Если кривая (3) непрерывна, x (t) – непрерывно дифференцируема, функция f непрерывна на g, то интеграл (2) существует и имеет место формула
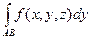 =
=  .
.
Доказательство. Для разбиения T ={ Tk }={(x (tk), y (tk), z (tk)} и промежуточных точек
{ X k }={(x (x k), y (x k), z (x k)} можно интегральные суммы представить в виде
 =
= 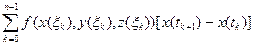 =
= 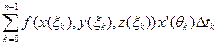
Последнюю сумму в этом равенстве можно представить в виде
 +
+ 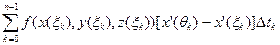 .
.
Здесь первая сумма является интегральной для интеграла 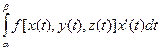 , а вторая может быть сделана меньше любого наперед заданного e >0 выбором достаточно мелкого разбиения в силу равномерной непрерывности функции
, а вторая может быть сделана меньше любого наперед заданного e >0 выбором достаточно мелкого разбиения в силу равномерной непрерывности функции 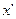 .
.
Замечание. Зачастую удобно рассматривать интегралы вида
 +
+ 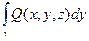 +
+ 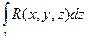 =
=  =
= 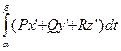 =
=
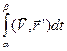 =
= 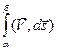 =
= 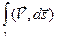 .
.
Интеграл 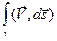 можно интерпретировать, как работу силового поля
можно интерпретировать, как работу силового поля 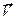
 вдоль пути g.
вдоль пути g.
2. Свойства криволинейного интеграла 2-го рода
Перечисляемые ниже свойства выписаны для интегралов вида 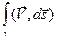 , но они справедливы и для интегралов
, но они справедливы и для интегралов 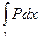 ,
, 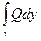 ,
, 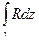 . Через g -- обозначается кривая, отличающаяся от g направлением обхода. Кривую g будем предполагать кусочно-гладкой, а функции P, Q, R непрерывными
. Через g -- обозначается кривая, отличающаяся от g направлением обхода. Кривую g будем предполагать кусочно-гладкой, а функции P, Q, R непрерывными
(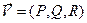 ), тогда
), тогда
1) 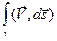 =
= 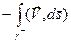
2) 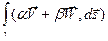 = a
= a 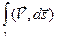 + b
+ b 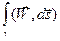
3) (Аддитивность по множеству) Если существует интеграл 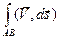 и кривая AB разбита точкой C на два участка AC, CB, то
и кривая AB разбита точкой C на два участка AC, CB, то
|
|
 =
= 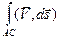 +
+ 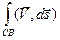 .
.
4) Если существует интеграл  , то
, то
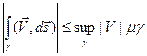 .
.
5) (Инвариантность интеграла относительно поворотов и сдвигов системы координат) При поворотах системы координат вокруг осей и при сдвигах криволинейный интеграл не меняется
Первое свойство следует непосредственно из определения криволинейного интеграла. Свойства 2)-3) доказываются так же, как и для обычных интегралов. Для кусочно гладкой кривой эти свойства следуют из свойств интегралов 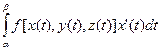 ,
, 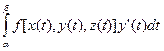 ,
, 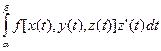 . Четвертое свойство будет доказано в следующем пункте.
. Четвертое свойство будет доказано в следующем пункте.
Замечание. Свойство аддитивности интеграла по множеству позволяет распространить утверждение теоремы 1 предыдущего пункта на кусочно-гладкие кривые.
3. Связь с интегралом 1-го рода.
Рассмотрим кусочно-гладкую кривую g и непрерывную функцию f (x, y, z), определенную на g. Рассмотрим разбиение { Tk }={ xk, yk, zk,} кривой g с промежуточными точками X ={ X k }.

D xk=xk+1 - xk= D lk cos a k. На рисунке отрезок BC проходит через точку Tk, параллельно оси Ox.
Поэтому
 =
= 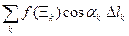
Слева стоят интегральные суммы для интеграла 2-го рода, а справа стоят суммы, которые при измельчении разбиения будут сходиться к интегралу 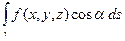 , где a = a (x, y, z) - угол, который образует касательный вектор к кривой g в точке (x, y, z) с осью Ox,
, где a = a (x, y, z) - угол, который образует касательный вектор к кривой g в точке (x, y, z) с осью Ox,  . Отсюда следует, что
. Отсюда следует, что
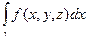 =
= 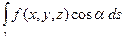 .
.
Докажем это.
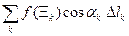 =
= 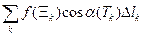 =
= 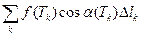 +
+ 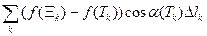 .
.
Первая сумма является интегральной для 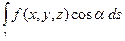 , вторая может быть сделана сколь угодно малой выбором достаточно мелкого разбиения (в силу равномерной непрерывности функции f [ x (t), y (t), z (t)] на [ a, b ]).
, вторая может быть сделана сколь угодно малой выбором достаточно мелкого разбиения (в силу равномерной непрерывности функции f [ x (t), y (t), z (t)] на [ a, b ]).
Аналогичные утверждения справедливы для интегралов по отношению к осям Oy, Oz. Откуда, в свою очередь, будет следовать равенство
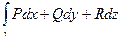 =
=  , (4)
, (4)
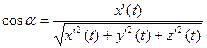 ,
, 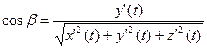 ,
, 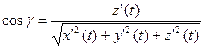 .
.
Обозначим орт вектора касательной 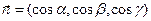 и введем понятие вектора элемента длины дуги
и введем понятие вектора элемента длины дуги 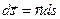 . В этих обозначениях интеграл справа в (4) может быть записан в виде
. В этих обозначениях интеграл справа в (4) может быть записан в виде 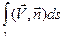 , это интеграл первого рода. Интеграл слева в (4) является интегралом второго рода и его принято обозначать
, это интеграл первого рода. Интеграл слева в (4) является интегралом второго рода и его принято обозначать 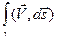 . Таким образом, формула (4) в векторном виде может быть записана следующим образом
. Таким образом, формула (4) в векторном виде может быть записана следующим образом
 =
=  .
.
Докажем четвертое свойство интеграла второго рода 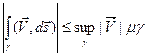 . Для интегральных сумм интеграла
. Для интегральных сумм интеграла  (второе определение) можно записать
(второе определение) можно записать
|
|
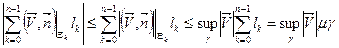 .
.
Определение. Кривая с заданным направлением обхода называется ориентированной кривой. Для замкнутой кривой, лежащей в плоскости z =0, положительным направлением обхода называется такое направление, при котором область, ограниченная этой кривой, остается слева.

Пример 1. (4225) Вычислить 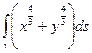 , g - дуга астроиды
, g - дуга астроиды 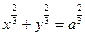 .
.
|
| Параметрическое уравнение астроиды |
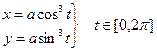
|
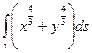 =
= 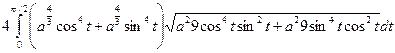 =
= 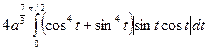 =
= 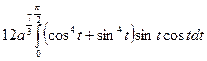 =
= 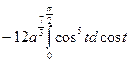 +
+ 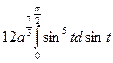 =
= 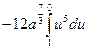 +
+  =
= 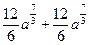 =
= 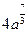
Пример 2. (4238)  , g - окружность
, g - окружность 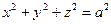 , x + y + z =0.
, x + y + z =0.
| Сделаем поворот системы координат на 45 градусов вокруг оси Oz. | Это означает переход к новой системе координат |
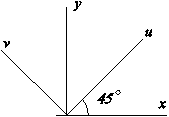
| 
|
Согласно свойству инвариантности интеграла относительно поворотов
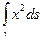 =
= 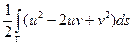 , где G - окружность u 2 + v 2 + w 2 = a 2,
, где G - окружность u 2 + v 2 + w 2 = a 2, 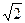 u + w =0. Отметим, что этим поворотом мы «избавились» от одного переменного в уравнении плоскости. Попробуем избавиться таким же способом от второго переменного. Так как
u + w =0. Отметим, что этим поворотом мы «избавились» от одного переменного в уравнении плоскости. Попробуем избавиться таким же способом от второго переменного. Так как  u + w =
u + w = 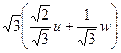 , то этого можно добиться, сделав поворот
, то этого можно добиться, сделав поворот
| Обратное отображение | |
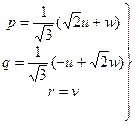
| 
|
Это соответствует повороту на угол b, для которого 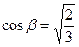 ,
,  .В новых координатах p, q, r уравнение плоскости будет иметь вид p = 0. Подинтегральная функция
.В новых координатах p, q, r уравнение плоскости будет иметь вид p = 0. Подинтегральная функция
u2-2uv+v2= 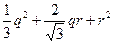 . Кривая лежит в плоскости p =0, поэтому в качестве параметризации возьмем полярные координаты
. Кривая лежит в плоскости p =0, поэтому в качестве параметризации возьмем полярные координаты
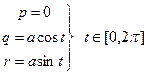
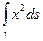 =
= 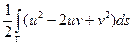 =
= 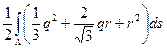 =
= 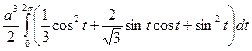 =
= 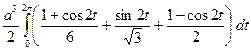 =
=  =
= 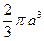 .
.
Пример 3. (4248) Вычислить интеграл
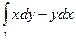 , где g - 1) отрезек g 1 = OA, O =(0,0), A =(1,2). 2) парабола g 2 ={ y =2 x 2 }, от O до A. 3) два отрезка g 3 + g 4: по оси Ox и вертикально вверх до точки A.
, где g - 1) отрезек g 1 = OA, O =(0,0), A =(1,2). 2) парабола g 2 ={ y =2 x 2 }, от O до A. 3) два отрезка g 3 + g 4: по оси Ox и вертикально вверх до точки A.
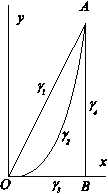
§3. Формула Грина
1.Формула Грина
Рассмотрим область типа A (см. рис.) D ={(x, y): y 1 (x) £ y £ y 2 (x), x Î [ a, b ]}, где y 1 (x) £ y 2 (x), две непрерывные функции на отрезке [ a, b ].
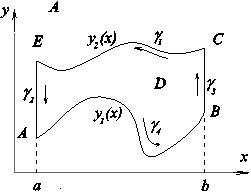
Границу этой области с положительным направлением обхода обозначим G. Пусть в области D задана функция P (x, y), непрерывная там вместе со своей частной производной 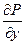 . Тогда справедлива формула
. Тогда справедлива формула
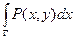 = -
= - 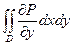 . (1)
. (1)
Доказательство. 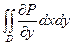 =
= 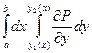 =
=  =
=  -
-  =
= 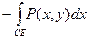
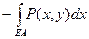 -
- 
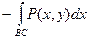 =
= 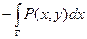 .
.
Здесь используются равенства 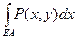 =0,
=0,  =0, следующие непосредственно из определения интеграла. Аналогично, можно показать, что для области типа B (см. рис.)
=0, следующие непосредственно из определения интеграла. Аналогично, можно показать, что для области типа B (см. рис.)
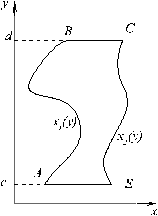
справедлива формула
 =
= 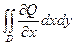 . (2)
. (2)
Если область является одновременно областью и типа A и типа B,

то из (1), (2) для поля 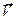 = (P, Q) получается формула
= (P, Q) получается формула
 (3)
(3)
Формулы (1), (2), (3) называются формулами Грина.
Замечание. Формула (3) верна и для областей более общего вида. В частности, если область можно разбить непрерывными кривыми на конечное число областей, для каждой из которых формула (3) справедлива, то эта формула будет верна и для всей области.
Для области, показанной на рисунке, можно сделать разрез, как показано на рисунке.
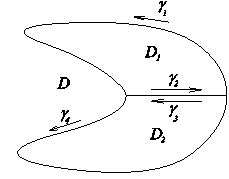
Область разбивается на две области D 1, D 2 , для которых справедлива формула Грина.
Введем обозначения ¶ D 1 = g 1 + g 2, ¶ D 2 = g 3 + g 4 = G, тогда ¶ D = g 1 + g 4. При этом 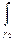 +
+ 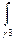 =0. Тогда
=0. Тогда
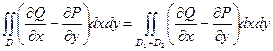 =
=  +
+ 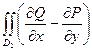 =
=  +
+ 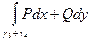 =
= 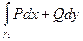 +
+ 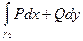 +
+ 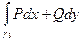 +
+ 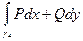 =
=  +
+  =
= 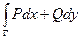 .
.
Пример 1. (4307) Вычислить 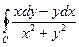 . Контур C оринтирован положительно. Рассмотреть два случая: контур не содержит начало координат, контур содержит начало координат.
. Контур C оринтирован положительно. Рассмотреть два случая: контур не содержит начало координат, контур содержит начало координат.
|
|
Обозначим через D область, ограниченную контуром C. Вычислим частные производные
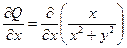 =
=  =
=  ,
,
 =
=  =
= 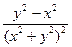 ,
,
Таким образом, в первом случае 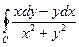 =
= 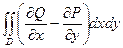 =0.
=0.
Во втором случае формула Грина не может быть использована, так как поле (P, Q) имеет особенность в начале координат, которая попадает в область интегрирования. Выберем круг с центром в начале координат и достаточно малого радиуса r так, чтобы он содержался в области D. Границу этого круга, ориентированную положительно, обозначим Cr. Произведем два разреза кусочно-гладкими кривыми, соединяющие какие либо две точки границы контура C с какими либо точками окружности Cr. На рисунки в качестве разрезов выбраны отрезки прямой и показаны обозначения для некоторых кривых, образовавшихся в результате этих разрезов. Отметим, что
C = C 1 + C 8,  = C 3 + C 6, C 2 =
= C 3 + C 6, C 2 = 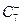 , C 4 =
, C 4 = 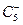 .
.

Внутри контуров C 1 + C 2 + C 3 + C 4 и C 5 + C 6 + C 7 + C 8 особенностей нет и, как было доказано, с Контур G = C 1 + C 2 + C 3 + C 4 + C 5 + C 6 + C 7 + C 8 не содержит внутри себя ни каких особенностей векторного поля (P, Q) и, поэтому к нему применима формула Грина
0 = 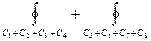 =
= 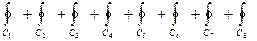 =
= 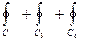 =
= 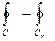 .
.
Таким образом. 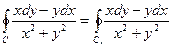 =
= 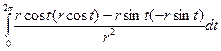 =
=  .
.
Пример 2. (4303) Вычислить 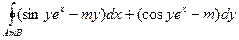 , где AmB – верхняя полуокружность x 2 + y 2 = ax, начало - A (a,0), конец – B (0,0).
, где AmB – верхняя полуокружность x 2 + y 2 = ax, начало - A (a,0), конец – B (0,0).

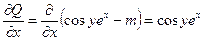 ,
, 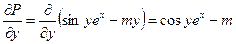 .
.  .
.
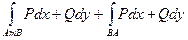 =
= 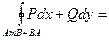
 =
= 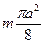 .
.
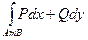 =
= 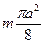
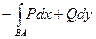 =
= 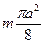
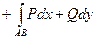 .
.
AB - имеет параметризацию 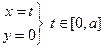 .
.
Тогда
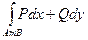 =
= 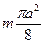 +
+ 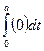 =
= 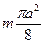 .
.
Пример 3. (4304) Вычислить 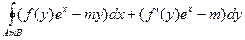 , где функция f (y) – непрерывно дифферинцированная на проекции кривой AmB функция (проекция на ось Oy), AmB – кривая, соединяющая точки A, B, ограничивающая вместе в отрезком AB область D.
, где функция f (y) – непрерывно дифферинцированная на проекции кривой AmB функция (проекция на ось Oy), AmB – кривая, соединяющая точки A, B, ограничивающая вместе в отрезком AB область D.

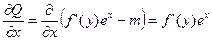 ,
, 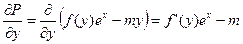 .
.  .
.
 =
= 
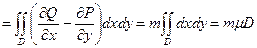 .
.
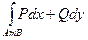 = m m D
= m m D  = m m D
= m m D 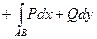 .
.
AB - имеет параметризацию 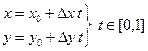 , A =(x 0, y 0), B =(x 1, y 1), D x = x 1 - x 0 , D y = y 1 - y 0.
, A =(x 0, y 0), B =(x 1, y 1), D x = x 1 - x 0 , D y = y 1 - y 0.
Тогда
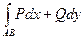 =
= 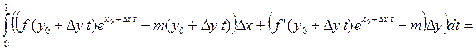
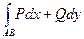 =
= 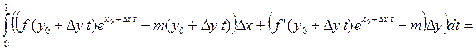

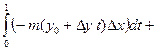
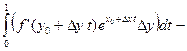
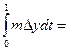
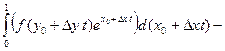
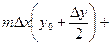


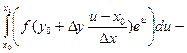

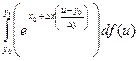 -
- 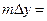
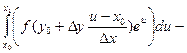

 =
= 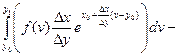
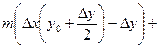
 =
= 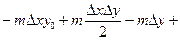
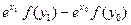 .
.
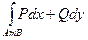 = m m D+
= m m D+ 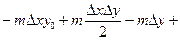
 .
.
2.Использование формулы Грина для вычисления площадей.
Если в качестве функций P, Q взять функции, для которых  , то получится формула для вычисления площади области, ограниченной кривой g.
, то получится формула для вычисления площади области, ограниченной кривой g.
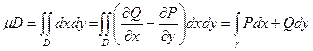 .
.
Можно предложить три варианта таких функций
1) Q = x, P =0 и тогда 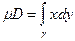 .
.
2) Q =0, P =- y и тогда 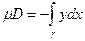 .
.
3) Q = 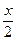 , P =
, P = 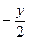 и тогда
и тогда 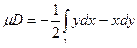 .
.
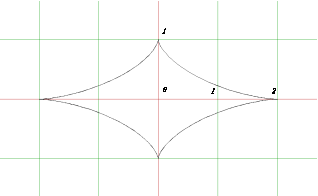
Пример 1. Вычислить площадь астроиды

| 
|
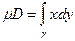 =
= 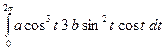 =
= 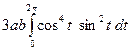 =
= 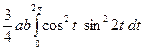 =
= 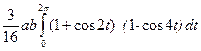 =
= 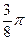 ab.
ab.
Пример 2. Вычислить площадь лемнискаты (x 2 + y 2)2= a 2 (x 2 - y 2).
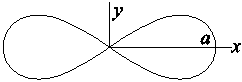
В полярных координатах 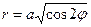 .
.
Параметризация правой ветви 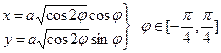 .
.
 =
= 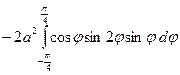 +
+  =
= 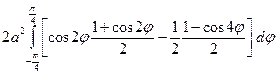 =
= 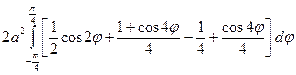 =
= 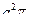 .
.
3. Условия независимости интеграла второго рода от пути интегрирования.
Определение. Область называется односвязной, если ее граница представляет собой связное множество. Область называется n -связной, если ее граница распадается на n - связных множеств.
Замечание. Формула Грина верна и для многосвязных областей.
Например, для области, показанной на рисунке произведены разрезы, соедеиняющие обе связные компоненты границы между собой.
Можно выписать цепочку равенств
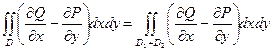 =
=  +
+ 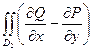 =
= 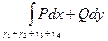 +
+  =
=  +
+  +
+ 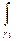 +
+ 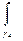 +
+  +
+  +
+ 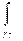 +
+ 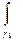 =
=  +
+ 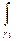 +
+  +
+ 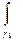 =
= 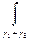 +
+ 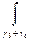 =
=  .
.
Замкнутая кривая называется контуром. Криволинейный интеграл второго рода в этом случае иногда обозначается 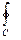 .
.
До конца этого пункта будем считать, что область D - открытое и односвязное множество, а функции P (x, y), Q (x, y) непрерывны в замыкании D вместе со своими производными 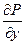 ,
, 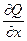 .
.
Лемма. Для того, чтобы интеграл
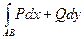 (4)
(4)
(A, B – любые точки из D) не зависел от пути интегрирования (а только от начальной и конечной точек A, B) необходимо и достаточно, чтобы по любой замкнутой кривой (по любому контуру) лежащей в D интеграл (4) был равен нулю
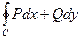 =0.
=0.
Интеграл 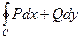 называется циркуляцией векторного поля V =(P, Q).
называется циркуляцией векторного поля V =(P, Q).
Доказательство (необходимость). Пусть (4) не зависит от пути интегрирования. Рассмотрим произвольный контур C, лежащий в области D и выберем две произвольные точки A, B на этом контуре. Тогда кривую C можно представить, как объединение двух кривых G 2 (из A в B, как на рисунке) и G 1 (тоже из A в B, но по другой ветви), C = 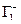 + G2.
+ G2.
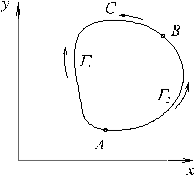
По условию 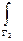 =
= 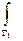 , кроме того
, кроме того  =
= 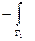 , поэтому
, поэтому 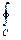 =
= 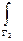 +
+  =
= 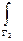 -
- 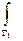 =0. Для доказательства достаточности рассмотрим две точки A, B в области D и два пути AB = G 2, AB = G 1 соединяющие эти две точки. Рассмотрим контур C =
=0. Для доказательства достаточности рассмотрим две точки A, B в области D и два пути AB = G 2, AB = G 1 соединяющие эти две точки. Рассмотрим контур C = 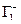 + G2. По условию
+ G2. По условию 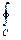 =0, откуда, с учетом соотношения
=0, откуда, с учетом соотношения 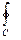 =
= 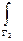 +
+  =
= 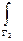 -
- 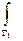 , следует требуемое равенство
, следует требуемое равенство 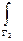 =
= 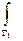 . В этом доказательстве предполагается, что кривые G 2, G 1 не пересекаются. Самостоятельно доказать это утверждение для случая, показанного на рисунке ниже
. В этом доказательстве предполагается, что кривые G 2, G 1 не пересекаются. Самостоятельно доказать это утверждение для случая, показанного на рисунке ниже
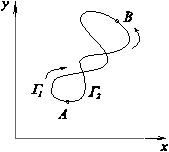
Теорема 1. Для того, чтобы криволинейный интеграл (4) не зависел от пути интегрирования в D, необходимо и достаточно чтобы
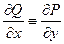 в области D. (5)
в области D. (5)
Достаточность. Если (5) выполнено, то формуле Грина для любого контура C будет
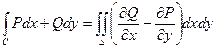 =0,
=0,
откуда по лемме следует требуемое утверждение.
Необходимость. По лемме для любого контура 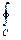 = 0. Тогда по формуле Грина для области D, ограниченной этим контуром
= 0. Тогда по формуле Грина для области D, ограниченной этим контуром  =0. По теореме о среднем 0=
=0. По теореме о среднем 0=  =
=  или
или  =
=  =0. Переходя к пределу, стягивая контур к точке, получим, что в этой точке
=0. Переходя к пределу, стягивая контур к точке, получим, что в этой точке 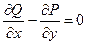 .
.
Теорема 2. Для того, чтобы криволинейный интеграл (4) не зависел от пути интегрирования в D, необходимо и достаточно чтобы подинтегральное выражение Pdx + Qdy являлось полным дифференциалом некоторой непрерывно дифференцируемой функции u (x, y) в области D
du = Pdx+Qdy (6)
Достаточность. Пусть (6) выполнено, тогда 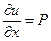 ,
, 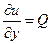 ,
, 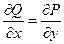 и можно сослаться на теорему 1.
и можно сослаться на теорему 1.
Необходимость. Пусть интеграл не зависит от пути интегрирования. Фиксируем некоторую точку A 0 в области D и определим функцию
u(A) = u(x,y)= 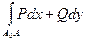 .
.
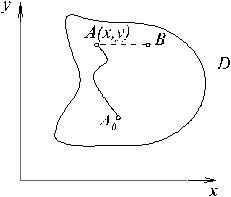
В этом случае
 , x Î [ x, x + D x ] (x Î [ x + D x, x ]). Таким образом, существует производная
, x Î [ x, x + D x ] (x Î [ x + D x, x ]). Таким образом, существует производная 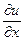 = P. Аналогично, проверяется, что
= P. Аналогично, проверяется, что 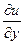 = Q. При сделанных предположениях функция u оказывается непрерывно - дифференцируемой и du = Pdx + Qdy.
= Q. При сделанных предположениях функция u оказывается непрерывно - дифференцируемой и du = Pdx + Qdy.
Замечание 1. Условие односвязности области D в сформулированных теоремах существенно.
Р
|
|
|

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!