§1. Тройные и n-кратные интегралы
1.Определение тройного и n-кратного интеграла
Пусть D кубируема, ее площадь будем обозначать m D, функция f (M) = f (x, y, z) определена и ограничена в области D. Предположим, что D разбита поверхностями на кубируемые подобласти Dk (совокупность { Dk } называется разбиением области D). В каждой из подобластей Dk выберем точку Mk =(x k, h k, z k) Î Dk. Полученный набор точек обозначим X ={ Mk }. Интегральной суммой для набора f, разбиения D, набора промежуточных точек X называется выражение
 (1)
(1)
Суммирование производится по всем областям разбиения. Величина l (D)= 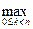 dDk называется характеристикой разбиения D. Здесь
dDk называется характеристикой разбиения D. Здесь 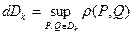 – диаметр множества Dk.
– диаметр множества Dk.
Условие Mk Î Dk, для всех k мы будем обозначать X Î D.
Определение. Предел интегральных сумм s (f, D, X) при l (D) ® 0 (если он существует и не зависит от выбора разбиений и промежуточных точек) называется тройным интегралом от функции f на D и обозначается
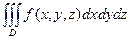 =
= 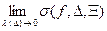 .
.
Можно использовать обозначение 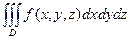 =
= 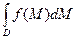 (вместо M можно использовать любую подходящую букву, например
(вместо M можно использовать любую подходящую букву, например 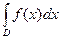 ).
).
Более точно это определение выглядит следующим образом:
$ J " e >0 $ d >0:(l (D)< d, X Î D) Þ | s (f, D, X) - J|< e.
Понятие длины, площади, объема распространяется и на области n - мерного евклидова пространства. В этом случае говорят об измеримости множества D n - мерного пространства и о его мере m D. Для измеримой области D и определенной на ней функции f (x)= f (x 1, x 2,…, xn) рассматривается разбиение этой области на измеримые множества { Dk }. В каждой из подобластей выбираются промежуточные точки x k =( ) Î Dk. Полученный набор точек обозначим X ={ x k }. Интегральной суммой для набора f, D, X называется выражение
) Î Dk. Полученный набор точек обозначим X ={ x k }. Интегральной суммой для набора f, D, X называется выражение
 (1)
(1)
Суммирование производится по всем областям разбиения. Величина l (D)=  dDk, где максимум берется по всем множествам разбиения, называется характеристикой разбиения D. Как и раньше,
dDk, где максимум берется по всем множествам разбиения, называется характеристикой разбиения D. Как и раньше,  – диаметр множества Dk, где точная верхняя грань берется по всевозможным точкам x =(x 1, x 2,…, xn), y =(y 1, y 2,…, yn) из Dk.
– диаметр множества Dk, где точная верхняя грань берется по всевозможным точкам x =(x 1, x 2,…, xn), y =(y 1, y 2,…, yn) из Dk.
Определение. Предел интегральных сумм s (f, D, X) при l (D) ® 0 (если он существует и не зависит от выбора разбиений и промежуточных точек) называется интегралом от функции f на D и обозначается
 =
= 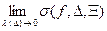 .
.
Для n -кратных интегралов имеют места свойства, аналогичные свойствам, сформулированным для двойных интегралов. Перечислим некоторые из этих свойств.
1) 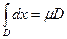
2) Если f и g интегрируемы на D, то f + g также интегрируема и
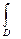 (f(x) + g(x))dx =
(f(x) + g(x))dx = 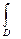 f(x)dx +
f(x)dx + 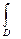 g(x)dx.
g(x)dx.
3) Если f интегрируема на D, то cf (x) также интегрируема и
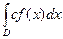 =c
=c  .
.
4) Если f интегрируема на D, то | f | также интегрируема и
|  | £
| £ 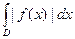 .
.
5) Если f и g интегрируемы на D и f £ g на D, то
 £
£  .
.
6) Если m £ f (x) £ M на D, то $ c Î [ m, M ]:
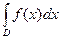 = c m D.
= c m D.
Следствие. Если f непрерывна на связном компакте D, то $ x Î D:
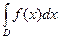 = f (x) m D.
= f (x) m D.
7) Непрерывная на компакте функция интегрируема на этом компакте.
8) Если m D = 0, то для любой ограниченной функции f будет выполнено
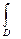 f(x) dx=0.
f(x) dx=0.
2. Сведение тройного интеграла к повторному для прямоугольного параллелепипеда
Пусть V – прямоугольный параллелепипед [ a, b ] ´ [ c, d ] ´ [ g, h ] и функция f (x, y, z) определена на V. Обозначим прямоугольник [ c, d ] ´ [ g, h ] через D.

Теорема. Если существует 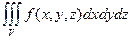 и для любого x Î [ a, b ] существует
и для любого x Î [ a, b ] существует 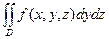 , то существует интеграл
, то существует интеграл 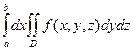 и имеет место равенство
и имеет место равенство
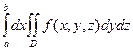 =
= 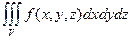 .
.
(здесь и в дальнейшем используются обозначения 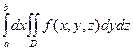 =
=  )
)
Доказательство. Рассмотрим разбиение D области V:
D ={ a = x 0 <…< xn = b; c = y 0 <…< ym = d; g = z 0 <…< zl = h }.
Полученные подобласти обозначим Vijk =[ xi, xi +1 ] ´ [ yj, yj +1 ] ´ [ zk, zk +1 ], i =0,…, n -1, j =0,…, m -1, z =0,…, l -1. Кроме того, будем использовать обозначения X =(x, y, z)
mijk = 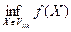 , Mijk =
, Mijk = 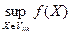 . Тогда для X Î Vijk справедливы неравенства mijk £ f (X) £ Mijk.
. Тогда для X Î Vijk справедливы неравенства mijk £ f (X) £ Mijk.
Для набора промежуточных точек { x i }, x i Î [ xi, xi +1 ] будет выполнено
mijk D yj D zk £  £ Mijk D yj D zk,
£ Mijk D yj D zk,
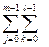 mijk D yj D zk £
mijk D yj D zk £ 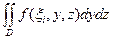 £
£ 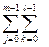 Mijk D yj D zk,
Mijk D yj D zk,
Домножая последние неравенства на D xi и суммируя, получим
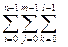 mijk D xi D yj D zk £
mijk D xi D yj D zk £ 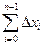
 £
£ 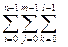 Mijk D xi D yj D zk.
Mijk D xi D yj D zk.
Средняя сумма является интегральной суммой для интеграла 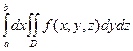 , крайние суммы являются суммами Дарбу для интеграла
, крайние суммы являются суммами Дарбу для интеграла 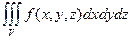 , откуда и следует требуемое утверждение.
, откуда и следует требуемое утверждение.
Аналогичные теоремы можно доказать для других порядков интегрирования. Таким образом, при выполнении соответствующих условий получаются равенства вида
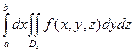 =
= 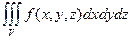 ,
,
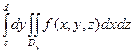 =
= 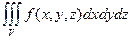 ,
,
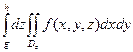 =
= 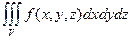 .
.
Через Dx, Dy, Dz обозначены проекции области V на координатные плоскости x =0, y =0, z =0, соответственно.
В свою очередь внутренние двойные интегралы можно представить в виде повторных. Для первого из написанных соотношений это будет выглядеть следующим образом
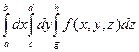 =
= 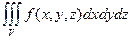 ,
,
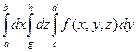 =
= 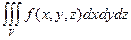 .
.
(используются обозначения 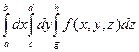 =
= 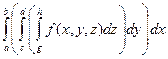 )
)
Теперь можно собирать внешние повторные интегралы в двойные, в результате получаться три равенства
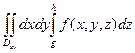 =
= 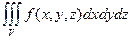 ,
,
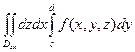 =
= 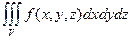 ,
,
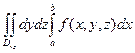 =
= 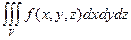 ,
,
Здесь Dxy =Dz =[a,b] ´ [c,d], Dzx=Dy =[g,h] ´ [a,b], Dyz =Dx = [c,d] ´ [g,h].
3. Сведение тройного интеграла к повторному интегралу для областей общего вида
Пусть V – область, расположенная между плоскостями x = a, x = b, Lx – плоскость параллельная координатной плоскости Oyz, проходящая через точку x. Для x Î [ a, b ] обозначим через Dx сечение V Ç Lx. Будем предполагать, что Dx квадрируемадля всех x Î [ a, b ]. При этих предположениях справедлива
Теорема. Если существует  и для " x Î [ a, b ] существует I (x)=
и для " x Î [ a, b ] существует I (x)= 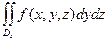 то существует и
то существует и 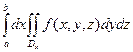 и
и
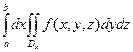 =
=  .
.
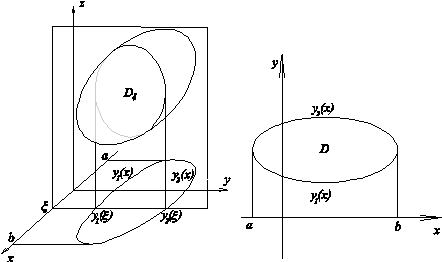
Доказательство. Обозначим через R =[ a, b ] ´ [ c, d ] ´ [ g, h ] прямоугольный параллелепипед, содержащий область V и определим на R функцию
f * (M)=  .
.
Тогда
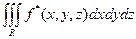 =
= 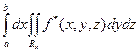 , Rx= [c,d] ´ [g,h].
, Rx= [c,d] ´ [g,h].
Для левого и правого интегралов справедливы равенства
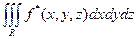 =
=  +
+ 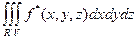 =
= 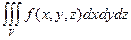 .
.
 =
= 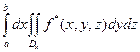 =
= 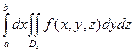 .
.
Замечание. Сечение Dx = V Ç Lx может быть задано в виде
Dx = {(y, z): y 1 (x) £ y £ y 2 (x), z 1 (x, y) £ z £ z 2 (x, y)}.


В этом случае пределы интегрирования в тройном интеграле можно расставить следующим образом 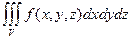 =
= 
 =
= 
 .
.
D – представляет собой проекцию V на плоскость z =0. Эту область можно также описать в виде
D = {(x,y):a £ x £ b, y1(x) £ y £ y2(x)}. Расставляя переменные x, y, z в другом порядке можно получить другие аналогичные формулы представления тройного интеграла через повторные.
4. Замена переменных в тройном и n -кратном интеграле
Пусть задано взаимно-однозначное, непрерывно - дифференцируемое отображение с якобианом, отличным от нуля
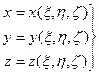 , (x, h, z) Î S
, (x, h, z) Î S
из S в V, где области S и V кубируемы. Тогда для объема области V справедлива формула
m V = 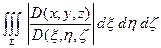 (4).
(4).
Из этой формулы и теоремы о среднем следует, что
 = m V =
= m V =  =
=  m S.
m S.
Откуда следует, что в любой точке области M 0 =(x 0, h 0, z 0)
 =
= 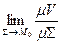 .
.
Теорема (о замене переменных). Если f интегрируема в V, то
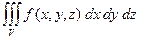 =
= 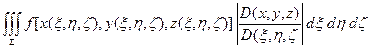 .
.
Доказательство. Интегралы справа и слева существуют. Интегрируемость функции F (x, h, z)= f [ x (x, h, z), y (x, h, z), z (x, h, z)] на S доказывается так же, как и в случае двойного интеграла. Выберем какое-либо разбиение { S j } области S и обозначим через { Vj } соответствующее разбиение области V. Согласно формуле (4)
m Vj = 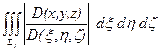 =
= 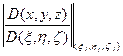 m S j.
m S j.
Полученные таким образом точки Mj = (x j, h j, z j) будем рассматривать как промежуточные точки для интегральных сумм функции F (x, h, z) и разбиения { S j }, а соответствующие точки Pj = (xj, yj, zj) для интегральных сумм функции f (x, y, z) и разбиения { Vj }. В этом случае
 .
.
Из этого равенства следует требуемое утверждение.
Пример 1. Цилиндрические координаты
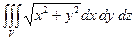 , x2+y2=z2, 0 £ z £ 1
, x2+y2=z2, 0 £ z £ 1
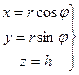 ,
,  .
.

В этом случае D = {(r, j, h): 0 £ j £ 2 p, 0 £ r £ z, " z Î [0,1]}.
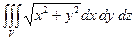 =
=  =
=  =
= 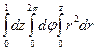 =
= 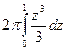 =
= 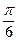 .
.
Пример 2. Сферические координаты
A=  , x2+y2+z2 £ 1, 0 £ x, 0 £ y, 0 £ z.
, x2+y2+z2 £ 1, 0 £ x, 0 £ y, 0 £ z.
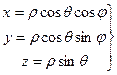 ,
, 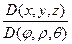 =
=  =
=
=-sin q (r 2 sin q cos q sin2 j + r 2 sin q cos q cos2 j)- r cos q (r cos2 q sin2 j + r cos2 q cos2 j) =
=-sin q r 2 sin q cos q - r cos q r cos2 q =- r 2 cos q.
A = 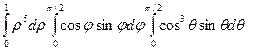 =
=  =
=  .
.
Пример 3. В интеграле  расставить пределы интегрирования в порядке dxdzdy и dzdxdy.
расставить пределы интегрирования в порядке dxdzdy и dzdxdy.
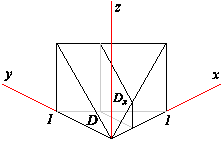
Пример 4. Заменить тройной интегрлал однократным 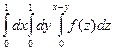
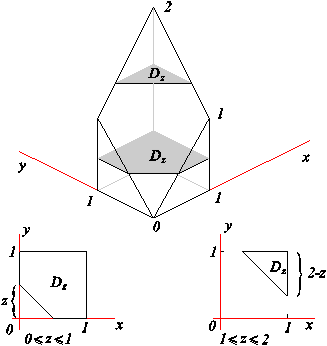
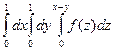 =
= 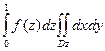 +
+ 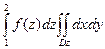 =
= 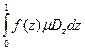 +
+  =
= 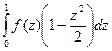 +
+ 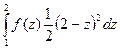
5. Замена переменных в общем случае
Рассмотрим регулярное отображение
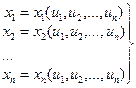 ( кратко x = x (u))
( кратко x = x (u))
из области S в область V. При измеримости областей S, V справедлива формула замены переменных
 =
=  ,
,
существование интегралов предполагается.



 (1)
(1)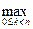 dDk называется характеристикой разбиения D. Здесь
dDk называется характеристикой разбиения D. Здесь 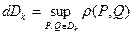 – диаметр множества Dk.
– диаметр множества Dk.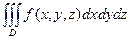 =
= 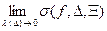 .
.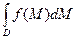 (вместо M можно использовать любую подходящую букву, например
(вместо M можно использовать любую подходящую букву, например 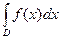 ).
). ) Î Dk. Полученный набор точек обозначим X ={ x k }. Интегральной суммой для набора f, D, X называется выражение
) Î Dk. Полученный набор точек обозначим X ={ x k }. Интегральной суммой для набора f, D, X называется выражение (1)
(1) dDk, где максимум берется по всем множествам разбиения, называется характеристикой разбиения D. Как и раньше,
dDk, где максимум берется по всем множествам разбиения, называется характеристикой разбиения D. Как и раньше,  – диаметр множества Dk, где точная верхняя грань берется по всевозможным точкам x =(x 1, x 2,…, xn), y =(y 1, y 2,…, yn) из Dk.
– диаметр множества Dk, где точная верхняя грань берется по всевозможным точкам x =(x 1, x 2,…, xn), y =(y 1, y 2,…, yn) из Dk. =
= 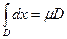
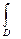 (f(x) + g(x))dx =
(f(x) + g(x))dx = 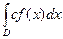 =c
=c  .
.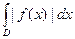 .
. .
.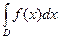 = f (x) m D.
= f (x) m D.
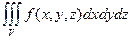 и для любого x Î [ a, b ] существует
и для любого x Î [ a, b ] существует 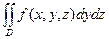 , то существует интеграл
, то существует интеграл 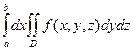 и имеет место равенство
и имеет место равенство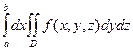 =
= 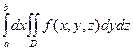 =
=  )
)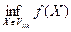 , Mijk =
, Mijk = 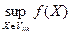 . Тогда для X Î Vijk справедливы неравенства mijk £ f (X) £ Mijk.
. Тогда для X Î Vijk справедливы неравенства mijk £ f (X) £ Mijk. £ Mijk D yj D zk,
£ Mijk D yj D zk,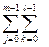 mijk D yj D zk £
mijk D yj D zk £ 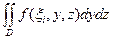 £
£ 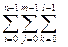 mijk D xi D yj D zk £
mijk D xi D yj D zk £ 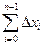
 £
£ 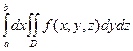 , крайние суммы являются суммами Дарбу для интеграла
, крайние суммы являются суммами Дарбу для интеграла 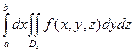 =
= 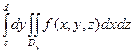 =
= 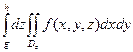 =
= 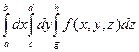 =
= 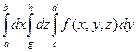 =
= 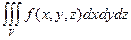 .
.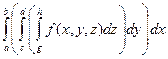 )
)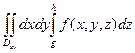 =
= 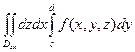 =
= 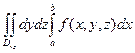 =
=  и для " x Î [ a, b ] существует I (x)=
и для " x Î [ a, b ] существует I (x)= 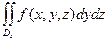 то существует и
то существует и 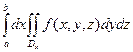 и
и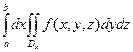 =
=  .
.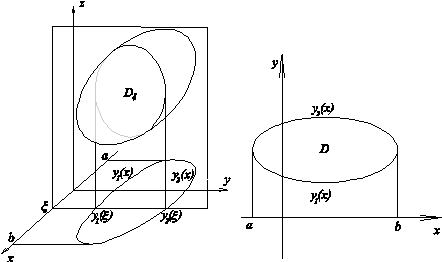
 .
. =
=  , Rx= [c,d] ´ [g,h].
, Rx= [c,d] ´ [g,h].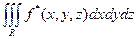 =
=  +
+ 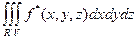 =
=  =
= 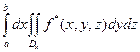 =
= 

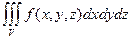 =
= 
 =
=  .
.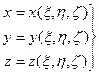 , (x, h, z) Î S
, (x, h, z) Î S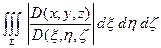 (4).
(4). = m V =
= m V =  =
=  m S.
m S. =
= 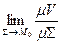 .
.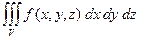 =
= 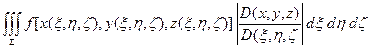 .
.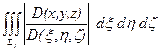 =
= 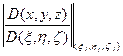 m S j.
m S j. .
.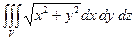 , x2+y2=z2, 0 £ z £ 1
, x2+y2=z2, 0 £ z £ 1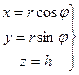 ,
,  .
.
 =
=  =
= 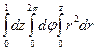 =
= 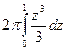 =
= 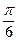 .
. , x2+y2+z2 £ 1, 0 £ x, 0 £ y, 0 £ z.
, x2+y2+z2 £ 1, 0 £ x, 0 £ y, 0 £ z.

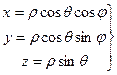 ,
, 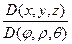 =
=  =
=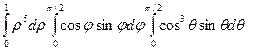 =
=  =
=  .
. расставить пределы интегрирования в порядке dxdzdy и dzdxdy.
расставить пределы интегрирования в порядке dxdzdy и dzdxdy.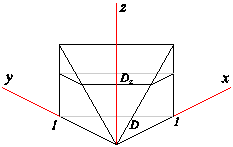
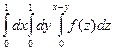

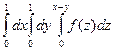 =
= 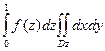 +
+ 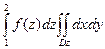 =
= 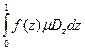 +
+  =
= 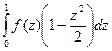 +
+ 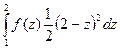
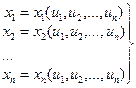 ( кратко x = x (u))
( кратко x = x (u)) =
=  ,
,


