ся движения воды в случае призматического русла.
Для призматического русла, то есть русла геометрические размеры которого постоянны и не изменяются по длине 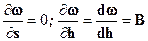
 (2.44)
(2.44)
Уравнение (2.44) является основным уравнением неравномерного плавноизменяющегося движения воды в призматических руслах с прямым уклоном дна.
2.4 Преобразование основного уравнения неравномерного движения воды
к виду, удобному для анализа
При анализе основного уравнения неравномерного движения воды в открытых руслах можно различать три случая: 1. i > 0; 2. i = 0; i < 0.
Русло с прямым уклоном дна (i > 0). Для этого случая уравнение получено в виде: 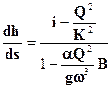 . Введем в рассмотрение вспомогательный поток с равномерным движение. Причем расход этого потока при заданной форме поперечного сечения русла, при заданном уклоне дна равен расходу Q, наблюдающемуся при неравномерном движении. Расход этого вспомогательного потока можно выразить известной зависимостью:
. Введем в рассмотрение вспомогательный поток с равномерным движение. Причем расход этого потока при заданной форме поперечного сечения русла, при заданном уклоне дна равен расходу Q, наблюдающемуся при неравномерном движении. Расход этого вспомогательного потока можно выразить известной зависимостью:

где Ко- модуль расхода, отвечающий нормальной глубине hо. Теперь основное уравнение неравномерного движения можно представить в следующем виде:
Числитель этого уравнения: 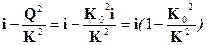 (2.45)
(2.45)
Преобразуем знаменатель правой части уравнения (2.44):

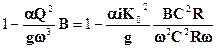 (то есть мы умножили числитель и знаменатель дроби на С2R). Учитывая, что К2 = w2С2R и w = Rc, получим:
(то есть мы умножили числитель и знаменатель дроби на С2R). Учитывая, что К2 = w2С2R и w = Rc, получим:

 (2.46)
(2.46)
где j = 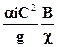 ; В соответствии с выражениями (2.45) и (2.46) представим уравнение (2.44) в следующем виде:
; В соответствии с выражениями (2.45) и (2.46) представим уравнение (2.44) в следующем виде:
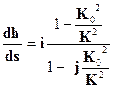 (2.47)
(2.47)
Используя показательный закон, запишем уравнение (2.47) в следующем виде:
 (2.48)
(2.48)
Учитывая, что при h = hk hkx - hоx = 0, hох = hk. Тогда:
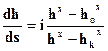 (2.49)
(2.49)
Русло с горизонтальным дном
Если призматическое русло имеет горизонтальное дно, основное уравнение неравномерного движения запишется следующим образом:
 (2.50)
(2.50)
Здесь также вводим в рассмотрение поток с равномерным движением и глубиной, равной критической и, следовательно, расход вспомогательного потока равен:
Q = K k  (2.51)
(2.51)
Тогда: 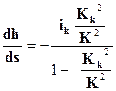 = -
= - 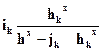 (2.52)
(2.52)
Учитывая, что при h = hk hx - hkx = 0, уравнение (2.52) запишется:
 (2.53)
(2.53)
Русло с обратным уклоном
В этом случае дифференциальное уравнение неравномерного движения воды в открытых руслах примет вид: 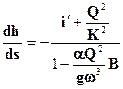 (2.54)
(2.54)
Введем в рассмотрение вспомогательный поток с равномерным движением, причем нормальную глубину 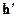 этого потока, отвечающую расходу Q при неравномерном движении в русле с заданной формой поперечного сечения, определим в предположении, что вода течет в обратном направлении. Тогда. Очевидно, будет:
этого потока, отвечающую расходу Q при неравномерном движении в русле с заданной формой поперечного сечения, определим в предположении, что вода течет в обратном направлении. Тогда. Очевидно, будет:
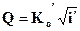 (2.55)
(2.55)
где  модуль расхода при глубине
модуль расхода при глубине  . При условии (2.55) уравнение (2.54) запишется так:
. При условии (2.55) уравнение (2.54) запишется так:  (2.56)
(2.56)
Возможные случаи соотношений между глубиной неравномерного движения h, нормальной глубиной h о и критической глубиной.
Каналы с прямым уклоном дна:
1. при i < ik, h > hk.
а) h > hо > hk
б) hо > h > hk
в) hо > hk > h
2. при iо > ik, hо < hk
а) h > hk > hо
б) hk > h > hо
в) hk > hо > h
4. при iо = ik, hо = hk возможны лишь два соотношения:
а) h > hk
б) h < hk
Если дно канала горизонтальное или имеет обратный уклон возможны лишь два соотношения:
а) h > hk
б) h < hk.
2.5. Исследование форм свободной поверхности потока в случае неравномерного плавноизменяющегося движения воды в призматических руслах.
1. Русло с прямым уклоном дна i > 0:
Выше мы получили уравнение (2.52) 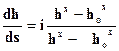 учитывая, что знаменатель правой части ётого уравнения при h = hk должен обращаться в нуль, можем записать:
учитывая, что знаменатель правой части ётого уравнения при h = hk должен обращаться в нуль, можем записать: 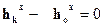 , откуда, допуская, что величина = const, получаем:
, откуда, допуская, что величина = const, получаем:

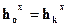
То есть мы получили уравнение (2.53) 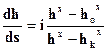 Это уравнение используем для анализа кривых свободной поверхности при прямом уклоне дна. Здесь различают три случая:
Это уравнение используем для анализа кривых свободной поверхности при прямом уклоне дна. Здесь различают три случая:
а) hо > hk; i < ik;
б) hо < hk; i > ik;
в) hо = hk; i = ik.
Рассмотрим, каковы будут кривые свободной поверхности в каждом из этих случаев. Случай а): представим себе продольный профиль заданного русла. Линии NN и КК разбивают всю область потока по высоте на три отдельные зоны а, b, c (рис. 2.14). В этом случае возможны три различные формы кривой свободной поверхности: кривая а1, когда h > hо > hk. Как видно, здесь мы имеем свободную поверхность, лежащую в зоне а выше линии NN. При этом получаем числитель и знаменатель уравнения (2.53) положительными. Следовательно 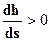 . Отсюда заключаем, что глубина потока вниз по течению должна увеличиваться, следовательно кривая а1 является кривой подпора. В практике такая кривая свободной по-
. Отсюда заключаем, что глубина потока вниз по течению должна увеличиваться, следовательно кривая а1 является кривой подпора. В практике такая кривая свободной по-
| верхности может появиться, например, после устройства плотины. Докажем теперь, что кривая а1 имеет две асимптоты: в верховой своей части линию NN и в низовой – горизонтальную прямую АB.
При стремлении h к hо (см. левый конец кривой а1) 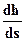 стремится к нулю, следовательно в стремится к нулю, следовательно в
|
верховой своей части кривая а 1 асимптотически приближается к линии NN, характеризуемой условием  . Вниз по течению глубины увеличиваются; при стремлении h к бесконечности
. Вниз по течению глубины увеличиваются; при стремлении h к бесконечности 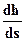 стремится к i:
стремится к i:
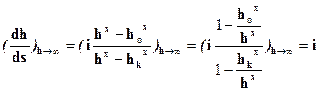 (2.57)
(2.57)
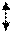










 Отсюда заключаем, что в низовой части кривая имеет горизонтальную асимптоту. Действительно горизонтальная прямая АВ (рис. 2.14) характеризуется условием
Отсюда заключаем, что в низовой части кривая имеет горизонтальную асимптоту. Действительно горизонтальная прямая АВ (рис. 2.14) характеризуется условием 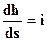 А В
А В
 ds dh
ds dh
Рис.2.15
Учитывая, что кривая а 1 имеет две асимптоты в виде линий NN и AB, можно утверждать, что выпуклость этой кривой направлена вниз. Так как кривая а1асимптотически приближается к прямой NN, то ясно, что подпор, вызванный плотиной или другим подпорным сооружением распространяется вверх по течению, теоретически на бесконечную длину. Однако на практике пренебрегают некоторой незначительной величиной 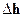 (рис.2.15), равной (0,01-0,02)hо и считают длину кривой подпора так как показано на рисунке.
(рис.2.15), равной (0,01-0,02)hо и считают длину кривой подпора так как показано на рисунке.
|
| |  |
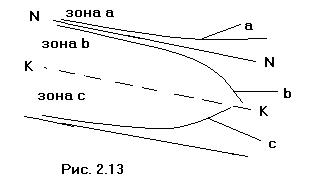
Здесь свободная поверхность потока лежит в зоне b (рис. 2.13). Так как hо>h>hk, то правая часть уравнения (2.49) получается отрицательной (dh/ds<0), то естькривая свободной поверхности является кривой спада. Поскольку при стремлении h к hо кривая асимптотически приближается к линии нормальных глубин NN, а при стремлении h к hk получаем 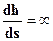 , то заключаем, что кривая b1 будет иметь вид, показанный на рисунке 2.13. Выпуклость этой кривой направлена вверх. Слева эта кривая имеет асимптотой линию NN, справа вертикальную касательную,
, то заключаем, что кривая b1 будет иметь вид, показанный на рисунке 2.13. Выпуклость этой кривой направлена вверх. Слева эта кривая имеет асимптотой линию NN, справа вертикальную касательную,
Кривая с 1 (рис 2.13) находится в зоне с. Так как h < hk < hо, то правая чаять этого уравнения оказывается положительной (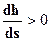 ) иБ следовательно, кривая с1 является кривой подпора. Кривая с1 асимптот не имеет; к линии КК она подходит, имея вертикальную касательную. Выпуклость кривой направлена вниз.
) иБ следовательно, кривая с1 является кривой подпора. Кривая с1 асимптот не имеет; к линии КК она подходит, имея вертикальную касательную. Выпуклость кривой направлена вниз.
Случай б) hо < hk и iо > ik. Исследование уравнения (2.53) показывает, что здесь, как в в случае а), возможны три вида кривых свободной поверхности.
Кривая а 2, когда h > hk > hо. Эта кривая лежит в зоне а (выше линии КК), 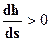 , следовательно глубина вниз по течению увеличивается, то есть кривая а2 является кривой подпора. Вниз по течению (при
, следовательно глубина вниз по течению увеличивается, то есть кривая а2 является кривой подпора. Вниз по течению (при  ) а2 асимптотически приближается к горизонтальной прямой: к линии КК (при
) а2 асимптотически приближается к горизонтальной прямой: к линии КК (при  ) она подходит, имея вертикальную касательную. Очевидно, что кривая а2 имеет выпуклость, направленную вверх. Эта кривая может появиться, например, после устройства преграды в русле, имеющем большой уклон (рис. 2.17)
) она подходит, имея вертикальную касательную. Очевидно, что кривая а2 имеет выпуклость, направленную вверх. Эта кривая может появиться, например, после устройства преграды в русле, имеющем большой уклон (рис. 2.17)
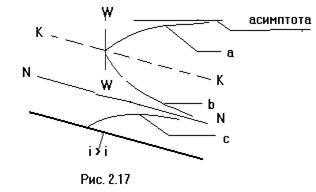
| Кривая b2 при h>hk>hо Эта кривая
Лежит в зоне b. Исследуя уравнение
(2.49) видим, что в данном случае
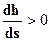 , следовательно, в этом случае
глубины потока вниз по течению
уменьшаются. Так как к линии КК
рассматриваемая кривая подходит,
имея вертикальную касательную WW,
а к линии NN эта кривая подходит , следовательно, в этом случае
глубины потока вниз по течению
уменьшаются. Так как к линии КК
рассматриваемая кривая подходит,
имея вертикальную касательную WW,
а к линии NN эта кривая подходит
|
асимптотически, то заключаем, что кривая b2 должна быть обращена выпуклостью вниз.
Кривая с 2, когда h<hо<hk
Кривая лежит в зоне с. Исследование уравнения (2.49) показывает, что 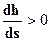 и, следовательно кривая с2 является кривой подпора. Она имеет асимптоту NN (рис.2.18)
и, следовательно кривая с2 является кривой подпора. Она имеет асимптоту NN (рис.2.18)
 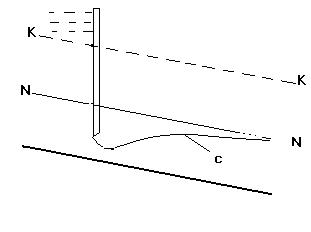 Рис 2.18 Рис 2.18
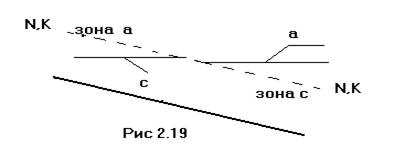
| Случай в) hо= hk; i = ik.
Здесь линии NN и КК совпадают (рис 2.19) и поэтому зона b исчезает. Остаются только зоны а и c. В соответствии с этим получаем две кривые: а3 и с3. Уравнение (2.49) принимает вид:
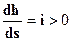 . Отсюда делаем вывод: обе кривые являются кривыми подпора (см. рис. 2.19)
-
- . Отсюда делаем вывод: обе кривые являются кривыми подпора (см. рис. 2.19)
-
-
|
Случай i = 0. В случае горизонтального русла равномерное движение невозможно и понятие нормальной глубины теряет смысл. В этом случае 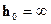 и поэтому зона а исчезает (линия NN располагается на бесконечно большом расстоянии от линии дна); остаются только зоны b и с. Следовательно при i = 0 возможны только две кривые (рис 2.20): кривая спада b0, лежащая в зоне b, когда h>hk и кривая подпора с0, лежащая в зоне с, когда h<hk
и поэтому зона а исчезает (линия NN располагается на бесконечно большом расстоянии от линии дна); остаются только зоны b и с. Следовательно при i = 0 возможны только две кривые (рис 2.20): кривая спада b0, лежащая в зоне b, когда h>hk и кривая подпора с0, лежащая в зоне с, когда h<hk

Примечание: при построении кривых свободной поверхности следует руководствоваться следующим правилом: кривая свободной поверхности к линии нормальных глубин всегда подходит асимптотически, никогда не пересекая ее а к линии критических глубин подходит, имея вертикальную касательную.





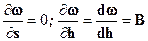
 (2.44)
(2.44)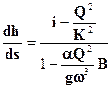 . Введем в рассмотрение вспомогательный поток с равномерным движение. Причем расход этого потока при заданной форме поперечного сечения русла, при заданном уклоне дна равен расходу Q, наблюдающемуся при неравномерном движении. Расход этого вспомогательного потока можно выразить известной зависимостью:
. Введем в рассмотрение вспомогательный поток с равномерным движение. Причем расход этого потока при заданной форме поперечного сечения русла, при заданном уклоне дна равен расходу Q, наблюдающемуся при неравномерном движении. Расход этого вспомогательного потока можно выразить известной зависимостью:
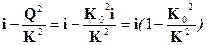 (2.45)
(2.45)
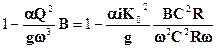 (то есть мы умножили числитель и знаменатель дроби на С2R). Учитывая, что К2 = w2С2R и w = Rc, получим:
(то есть мы умножили числитель и знаменатель дроби на С2R). Учитывая, что К2 = w2С2R и w = Rc, получим: (2.46)
(2.46)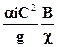 ; В соответствии с выражениями (2.45) и (2.46) представим уравнение (2.44) в следующем виде:
; В соответствии с выражениями (2.45) и (2.46) представим уравнение (2.44) в следующем виде: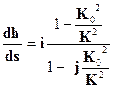 (2.47)
(2.47) (2.48)
(2.48)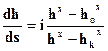 (2.49)
(2.49) (2.50)
(2.50) (2.51)
(2.51)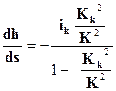 = -
= - 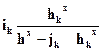 (2.52)
(2.52) (2.53)
(2.53)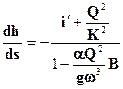 (2.54)
(2.54) 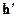 этого потока, отвечающую расходу Q при неравномерном движении в русле с заданной формой поперечного сечения, определим в предположении, что вода течет в обратном направлении. Тогда. Очевидно, будет:
этого потока, отвечающую расходу Q при неравномерном движении в русле с заданной формой поперечного сечения, определим в предположении, что вода течет в обратном направлении. Тогда. Очевидно, будет: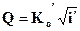 (2.55)
(2.55)  модуль расхода при глубине
модуль расхода при глубине  . При условии (2.55) уравнение (2.54) запишется так:
. При условии (2.55) уравнение (2.54) запишется так:  (2.56)
(2.56)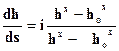 учитывая, что знаменатель правой части ётого уравнения при h = hk должен обращаться в нуль, можем записать:
учитывая, что знаменатель правой части ётого уравнения при h = hk должен обращаться в нуль, можем записать: 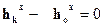 , откуда, допуская, что величина = const, получаем:
, откуда, допуская, что величина = const, получаем: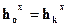
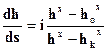 Это уравнение используем для анализа кривых свободной поверхности при прямом уклоне дна. Здесь различают три случая:
Это уравнение используем для анализа кривых свободной поверхности при прямом уклоне дна. Здесь различают три случая: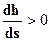 . Отсюда заключаем, что глубина потока вниз по течению должна увеличиваться, следовательно кривая а1 является кривой подпора. В практике такая кривая свободной по-
. Отсюда заключаем, что глубина потока вниз по течению должна увеличиваться, следовательно кривая а1 является кривой подпора. В практике такая кривая свободной по-
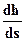 стремится к нулю, следовательно в
стремится к нулю, следовательно в
 . Вниз по течению глубины увеличиваются; при стремлении h к бесконечности
. Вниз по течению глубины увеличиваются; при стремлении h к бесконечности 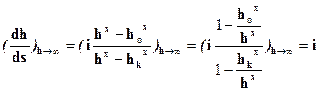 (2.57)
(2.57)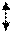










 Отсюда заключаем, что в низовой части кривая имеет горизонтальную асимптоту. Действительно горизонтальная прямая АВ (рис. 2.14) характеризуется условием
Отсюда заключаем, что в низовой части кривая имеет горизонтальную асимптоту. Действительно горизонтальная прямая АВ (рис. 2.14) характеризуется условием 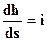 А В
А В  ds dh
ds dh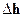 (рис.2.15), равной (0,01-0,02)hо и считают длину кривой подпора так как показано на рисунке.
(рис.2.15), равной (0,01-0,02)hо и считают длину кривой подпора так как показано на рисунке.




 Кривая b1:
Кривая b1:
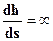 , то заключаем, что кривая b1 будет иметь вид, показанный на рисунке 2.13. Выпуклость этой кривой направлена вверх. Слева эта кривая имеет асимптотой линию NN, справа вертикальную касательную,
, то заключаем, что кривая b1 будет иметь вид, показанный на рисунке 2.13. Выпуклость этой кривой направлена вверх. Слева эта кривая имеет асимптотой линию NN, справа вертикальную касательную,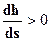 ) иБ следовательно, кривая с1 является кривой подпора. Кривая с1 асимптот не имеет; к линии КК она подходит, имея вертикальную касательную. Выпуклость кривой направлена вниз.
) иБ следовательно, кривая с1 является кривой подпора. Кривая с1 асимптот не имеет; к линии КК она подходит, имея вертикальную касательную. Выпуклость кривой направлена вниз.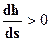 , следовательно глубина вниз по течению увеличивается, то есть кривая а2 является кривой подпора. Вниз по течению (при
, следовательно глубина вниз по течению увеличивается, то есть кривая а2 является кривой подпора. Вниз по течению (при  ) а2 асимптотически приближается к горизонтальной прямой: к линии КК (при
) а2 асимптотически приближается к горизонтальной прямой: к линии КК (при  ) она подходит, имея вертикальную касательную. Очевидно, что кривая а2 имеет выпуклость, направленную вверх. Эта кривая может появиться, например, после устройства преграды в русле, имеющем большой уклон (рис. 2.17)
) она подходит, имея вертикальную касательную. Очевидно, что кривая а2 имеет выпуклость, направленную вверх. Эта кривая может появиться, например, после устройства преграды в русле, имеющем большой уклон (рис. 2.17) 
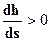 и, следовательно кривая с2 является кривой подпора. Она имеет асимптоту NN (рис.2.18)
и, следовательно кривая с2 является кривой подпора. Она имеет асимптоту NN (рис.2.18)
 Рис 2.18
Рис 2.18
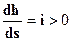 . Отсюда делаем вывод: обе кривые являются кривыми подпора (см. рис. 2.19)
-
-
. Отсюда делаем вывод: обе кривые являются кривыми подпора (см. рис. 2.19)
-
-
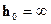 и поэтому зона а исчезает (линия NN располагается на бесконечно большом расстоянии от линии дна); остаются только зоны b и с. Следовательно при i = 0 возможны только две кривые (рис 2.20): кривая спада b0, лежащая в зоне b, когда h>hk и кривая подпора с0, лежащая в зоне с, когда h<hk
и поэтому зона а исчезает (линия NN располагается на бесконечно большом расстоянии от линии дна); остаются только зоны b и с. Следовательно при i = 0 возможны только две кривые (рис 2.20): кривая спада b0, лежащая в зоне b, когда h>hk и кривая подпора с0, лежащая в зоне с, когда h<hk




