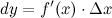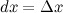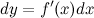Пример 1. Сколько трехзначных чисел можно составить из 4 цифр: 1, 2, 3, 4? Решение. Перечислим с помощью схемы все возможные числа:  Видим, что всего данных чисел 43 = 64, где 4 — количество элементов исходного множества, а 3 — число выбранных элементов.Данный пример является иллюстрацией к следующему понятию:
Видим, что всего данных чисел 43 = 64, где 4 — количество элементов исходного множества, а 3 — число выбранных элементов.Данный пример является иллюстрацией к следующему понятию:
Размещениями из n элементов по k называются упорядоченные выборки, каждое из которых содержит k элементов из n данного множества. Размещения отличаются друг от друга либо порядком элементов, либо самими элементами.Если некоторые элементы данного множества могут повторяться в размещении, то такие размещения называются кортежами или размещениями с повторениями. Число элементов в размещении называют его длиной.Размещениями с повторениями называют упорядоченную выборку, состоящую из n не обязательно различных элементов. Пусть дано множество M = {a1, а2, а3,..., аn}. Сколько кортежей длины k можно составить из n элементов этого множества?Решение.Первый элемент каждого кортежа мы можем выбрать n способами, записав на первое место любой из n элементов. Второй элемент тоже можно выбрать n способами и т.д. Значит, общее число кортежей из множества n элементов, по k элементов в каждом, будет равно nk. Число кортежей из n по k с учетом их порядка обозначается 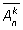 , и называют числом размещений с повторениями из n элементов по k:
, и называют числом размещений с повторениями из n элементов по k:  .В примере 1:
.В примере 1: 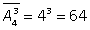 .
.
Перестановки с повторениями Пример 2. Сколько четырехзначных чисел можно составить из 4 цифр: 1, 2, 3, 4? Решение. Перечислим с помощью схемы все возможные числа: 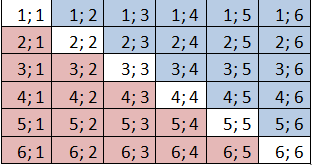 Видим, что всего данных чисел 44 = 256.Данный пример является иллюстрацией к следующему понятию, которое является частным случаем, когда наше основное множество состоит из различных элементов:Размещения с повторениями из n не обязательно различных элементов основного множества по n принято называть перестановками с повторениями. Число перестановок с повторениями обозначают
Видим, что всего данных чисел 44 = 256.Данный пример является иллюстрацией к следующему понятию, которое является частным случаем, когда наше основное множество состоит из различных элементов:Размещения с повторениями из n не обязательно различных элементов основного множества по n принято называть перестановками с повторениями. Число перестановок с повторениями обозначают  .Заметим,
.Заметим,  . Общее число перестановок с повторениями из n элементов равно
. Общее число перестановок с повторениями из n элементов равно 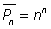 .В примере 2:
.В примере 2: 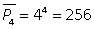 . Пример 3. Сколько семизначных чисел можно составить из 7 цифр: 1; 1; 2; 2; 2; 3; 4? Решение. Заметим, что «1» повторяется 2 раза, «3» — три раза, а «3» и «4» — по одному. На этот случай существует другая формула перестановок с повторениями.В общем случае, когда в нашем основном множестве какие-то элементы могут повторяться используют понятие:
. Пример 3. Сколько семизначных чисел можно составить из 7 цифр: 1; 1; 2; 2; 2; 3; 4? Решение. Заметим, что «1» повторяется 2 раза, «3» — три раза, а «3» и «4» — по одному. На этот случай существует другая формула перестановок с повторениями.В общем случае, когда в нашем основном множестве какие-то элементы могут повторяться используют понятие:
Размещения без повторений (Размещения) Пример 4. Сколько трехзначных чисел, в которых цифры не повторяются, можно составить из 4 цифр: 1, 2, 3, 4? Решение. Перечислим с помощью схемы все возможные числа: 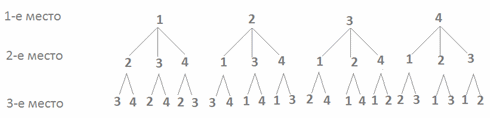 Видим, что всего данных чисел 4·3·2 = 24.Данный пример является иллюстрацией к следующему понятию:
Видим, что всего данных чисел 4·3·2 = 24.Данный пример является иллюстрацией к следующему понятию:
Пусть множество M = {a1, а2, а3,..., аn}. Сколько размещений без повторения элементов, по k элементов в каждом, можно составить из элементов этого множества?Решение.На первое место можно записать любой элемент из М. Значит, имеем n возможностей. На второе место — любой элемент, кроме выбранного на первое место. Итак, при каждом выборе первого элемента для выбора второго имеем n - 1 возможностей, т. е. для выбора двух элементов имеем n(n — 1) возможностей. При каждом выборе первых двух элементов для выбора третьего элемента имеем n — 2 возможностей и т. д. На послед нее k-е место можно записать любой элемент, кроме выбранных k — 1 элементов на предыдущие места, т.е. для его выбора имеем n — (k — 1) = n — k + 1 возможностей. Следовательно, всего размещений из n по k элементов будетAnk = n(n — 1)(n — 2)…(n — k + 1). Полученное выражение состоит из k последовательных натуральных множителей, наибольший из которых равен n. Умножив и разделив полученное выражение на (n — k)! получим: 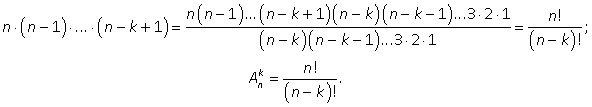
Размещениями называют упорядоченную выборку k элементов, из n различных элементов основного множества.Число всех выборов k элементов из n различных элементов данного множества с учетом их порядка обозначают Аnk и называют числом размещений из n элементов по k.
В примере 4: A43 = 4! / (4-3)! = 4·3·2 = 24.
Перестановки без повторений (Перестановки) Пример 5. Сколько четырехзначных чисел, в которых цифры не повторяются, можно составить из 4 цифр: 1, 2, 3, 4? Решение. Перечислим с помощью схемы все возможные числа: 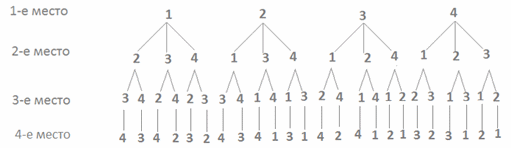 Видим, что всего данных чисел 4 · 3 · 2 · 1 = 24.Данный пример является иллюстрацией к следующему понятию:Размещения из n элементов по n принято называть перестановками. Иначе, перестановки — это упорядоченные множества из n различных элементов основного множества по n. Перестановки отличаются друг от друга только порядком элементов. Число перестановок принято обозначать Рn. Общее число перестановок из n элементов равно Pn = n!.
Видим, что всего данных чисел 4 · 3 · 2 · 1 = 24.Данный пример является иллюстрацией к следующему понятию:Размещения из n элементов по n принято называть перестановками. Иначе, перестановки — это упорядоченные множества из n различных элементов основного множества по n. Перестановки отличаются друг от друга только порядком элементов. Число перестановок принято обозначать Рn. Общее число перестановок из n элементов равно Pn = n!.
В примере 5: P4 = 4! = 4·2·3·1 = 24.
Неупорядоченные выборки.(Одновременный выбор). Сочетания без повторений. (Сочетания) Пример 6. Сколько трехэлементных подмножеств, различающихся хотя бы одним элементом друг от друга и без учета порядка в подмножестве, можно составить из 4 цифр: 1, 2, 3, 4? Решение. Перечислим все полученные подмножества:  (1, 2, 3), (1, 2, 4), (1, 3, 4), (2, 3, 4).Видим, что всего получилось 4 подмножества.Данный пример является иллюстрацией к следующему понятию:
(1, 2, 3), (1, 2, 4), (1, 3, 4), (2, 3, 4).Видим, что всего получилось 4 подмножества.Данный пример является иллюстрацией к следующему понятию:
Сочетания. Сочетаниями из n элементов по k называются соединения, каждое из которых содержит k элементов из данного множества n элементов и отличается от других хотя бы одним элементом. В сочетаниях нас интересуют только сами элементы множества и не интересует их порядок. Важно, какие конкретно элементы множества входят в каждое соединение.Число сочетаний, т.е. число всех различных подмножеств длины k из данного множества, содержащего n элементов, обозначается Сnk. Легко видеть, что если мы возьмем все сочетания из n по k и в каждом из них упорядочим элементы всеми возможными способами, т.е. из каждого сочетания получим все возможные перестановки, то получим все размещения из n элементов по k. Значит,Ank = Сnk·Pk. Отсюда 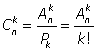 или
или 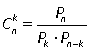 . Иначе
. Иначе  В примере 6:
В примере 6: 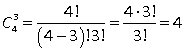 .
.
Пример 7. Сколькими способами можно выбрать к предметов из n?Например:
а) одновременно вынимают две карты из колоды: C362 = 36! / (36 - 2)!2! = (36 ∙ 35) / 2 = 630;б) наугад зачеркивают 6 чисел из 49: C496 = 49! / 43! ∙ 6! = 13 980 000;в) случайно отбирают трех человек из 25: C253 = 25! / (22! ∙ 3!) = 2 300.
Сочетания с повторениямиСочетания с повторениями — неупорядоченная выборка, состоящая из n необязательно различных элементов. Обозначается 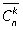 .
.  ,где n — количество необязательно различных элементов основного множества, k — количество выбираемых. Пример 8. Сколько будет костей в игре домино, если использовать, только четыре цифры 1, 2, 3, 4? Решение. Используем формулу сочетаний с повторениями:
,где n — количество необязательно различных элементов основного множества, k — количество выбираемых. Пример 8. Сколько будет костей в игре домино, если использовать, только четыре цифры 1, 2, 3, 4? Решение. Используем формулу сочетаний с повторениями:  Ответ:
Ответ:
10.Задачи для тренировки
Пример 9. Сколько четырехзначных чисел можно составить из 9 цифр: 1, 2, 3, 4, 5, 6, 7, 8, 9? Решение. Цифры в числах могут повторяться, и число зависит от порядка цифр в его записи. Значит, это размещения с повторениями, т.е. кортежи. Их число 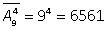 .Ответ:
.Ответ:
6561. Пример 10. В чемпионате участвует 12 команд. Сколькими различными способами могут быть распределены три различные медали?Решение.Это размещения без повторения, т.к. одна команда не может занять два или три места сразу. А123 = 12 · 11 · 10 = 1320.Ответ:
1320. Пример 11. В семье 6 человек. За столом 6 стульев. В семье решили каждый вечер рассаживаться на эти 6 стульев по-новому. Сколько дней члены семьи смогут делать это без повторений?Решение.Одного человека мы можем посадить только один раз. Значит, имеем перестановки без повторений. Одно размещение от другого может отличаться только порядком размещения людей, т.е. имеем перестановки 6 элементов: P6= 6! = 720.Ответ:
720. Пример 12. Сколькими способами из класса, в котором учатся 30 школьников, можно выбрать капитана команды для математических соревнований и его заместителя?Решение.
1-й способ: на роль капитана может быть выбран любой из 30 учащихся, а его заместитель — любой из 29 оставшихся учеников. Таким образом, получаем 30 · 29 = 870 способов.2-й способ: порядок важен, тогда по формуле числа размещений имеем  способов.
способов.
Ответ: 870. Пример 13. Сколькими способами из класса, в котором учатся 30 школьников, можно выбрать двоих для участия в математической олимпиаде?Решение.
1-й способ: нам не важно, кто капитан, а кто заместитель, нам нужны всего лишь два участника, поэтому получаем, что у нас каждая пара учащихся в произведении повторяется два раза. Поэтому ответом для второй задачи будет (30 · 29): 2 = 435.
2-й способ: без учета порядка применим формулу числа сочетаний 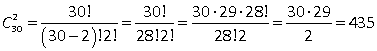 .
.
Ответ:
435. Пример 14. Сколько трехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаются одновременно), если на нем всего 10 цифр?Решение.Так как кнопки нажимаются одновременно, то выбор этих кнопок — сочетание. Отсюда возможно  вариантов.Ответ:
вариантов.Ответ:
120. Пример 15. Три медведя выбегают из дома, догоняя девочку. Сколькими способами они смогут это сделать?Решение.Порядок выбегания из дома задает нумерацию трех медведей числами 1 2 3. Таких нумераций 3! = 6.Ответ:
6. Пример 16. Сколькими способами можно построить пятерых человек в шеренгу?Решение.По формуле числа перестановок имеем Р5 = 5 · 4 · 3 · 2 · 1 = 120.Ответ:
120. Пример 17. Сколькими способами 4 вора могут по одному разбежаться на все 4 стороны?Решение.Стороны фиксированы, например юг, север, запад, восток или для простоты 1, 2, 3, 4. Порядок разбегания по ним задает нумерацию 4-х воров числами 1, 2, 3, 4. Таких нумераций имеется 4! = 24.Ответ:
24. Пример 18. 11 футболистов строятся перед началом матча. 1-м — обязательно капитан, 2-м — обязательно вратарь, а остальные — случайным образом. Сколько существует способов построения?Решение.Капитана и вратаря строить не надо, т.к. их места фиксированы. 9 футболистов (все, кроме капитана и вратаря) надо расставить на 9 мест — с 3-го по 11-е. Всего имеется 9! = 362 880 таких перестановок.Ответ:
362 880. Пример 19. В классе 27 учеников, из которых нужно выбрать троих. Сколькими способами это можно сделать, если:
а) 1-й ученик должен решить задачу, 2-й — сходить за мелом, 3-й — пойти дежурить в столовую;б) им следует спеть хором?
Решение.
а) порядок важен: А273 = 27 · 26 · 25 = 17 550;б) порядок неважен: С273 = (27 · 26 · 25) / (3 · 2) = 2 925.
Ответ: а) 17 550, б) 2 925. Пример 20. В коридоре 3 лампочки. Сколько существует различных способов освещения коридора? (включая случай, когда все три не горят) Решение.
1-й способ: пронумеруем лампочки. 1-я: горит или не горит (2 исхода), 2-я: горит или не горит (2 исхода), 3-я: горит или не горит (2 исхода). Лампочки горят или нет независимо друг от друга. По правилу умножения: 2 · 2 · 2 = 8.2-й способ: приведем дерево вариантов данной задачи: 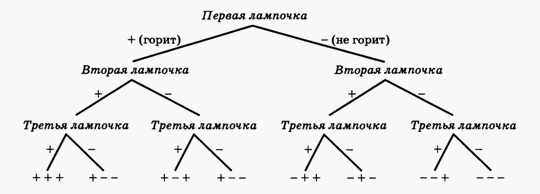 Например, (+ - +) означает, что горят 1-я и 3-я, (---) – не горит ни одна и т.д. в нашем случае у трехэлементного множества 23 = 8 подмножеств.
Например, (+ - +) означает, что горят 1-я и 3-я, (---) – не горит ни одна и т.д. в нашем случае у трехэлементного множества 23 = 8 подмножеств.
Пример 21. У бармена есть 6 сортов зеленого чая. Для проведения чайной церемонии требуется подать зеленый чай ровно 3 различных сортов. Сколькими способами бармен может выполнить заказ?Решение.Тут все просто: есть n = 6 сортов, из которых надо выбрать k = 3 сорта. Число сочетаний можно найти по формуле: 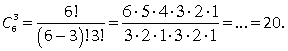 Ответ:
Ответ:
20. Пример 22. В чемпионате по футболу 7 команд. Каждая команда играла с каждой один раз. Сколько всего было игр?Решение.Порядок выбора не имеет значения, т.е. если выбраны две команды, то неважно, какая из них первая, а какая — вторая:  .Ответ:
.Ответ:
21. Пример 23. Сколько всего исходов, если друг за другом из колоды вынимают две карты, не возвращая карту обратно (выбор без возвращения)? Решение. 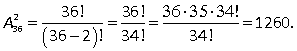 Ответ:
Ответ:
1260. Пример 24. Сколько существует всего исходов, если из колоды вынимают две карты одновременно?Решение.Порядок не важен, значит: 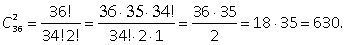
Дифференциал функции
Пусть функция  дифференцируема в точке
дифференцируема в точке  , то есть приращение этой функции можно представить в виде суммы двух слагаемых: линейного относительно
, то есть приращение этой функции можно представить в виде суммы двух слагаемых: линейного относительно 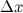 и нелинейного членов:
и нелинейного членов:

где  при
при 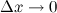 .
.
Определение
Дифференциалом функции называется линейная относительно 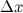 часть приращения функции. Она обозначается как
часть приращения функции. Она обозначается как 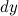 или
или 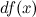 . Таким образом:
. Таким образом:
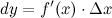
Замечание
Дифференциал функции составляет основную часть ее приращения.
Замечание
Наряду с понятием дифференциала функции вводится понятие дифференциала аргумента. По определению дифференциал аргумента есть приращение аргумента:
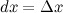
Замечание
Формулу для дифференциала функции можно записать в виде:
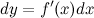
Отсюда получаем, что

Итак, это означает, что производная может быть представлена как обыкновенная дробь - отношение дифференциалов функции и аргумента.



 Видим, что всего данных чисел 43 = 64, где 4 — количество элементов исходного множества, а 3 — число выбранных элементов.Данный пример является иллюстрацией к следующему понятию:
Видим, что всего данных чисел 43 = 64, где 4 — количество элементов исходного множества, а 3 — число выбранных элементов.Данный пример является иллюстрацией к следующему понятию: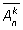 , и называют числом размещений с повторениями из n элементов по k:
, и называют числом размещений с повторениями из n элементов по k:  .В примере 1:
.В примере 1: 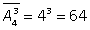 .
. Видим, что всего данных чисел 44 = 256.Данный пример является иллюстрацией к следующему понятию, которое является частным случаем, когда наше основное множество состоит из различных элементов:Размещения с повторениями из n не обязательно различных элементов основного множества по n принято называть перестановками с повторениями. Число перестановок с повторениями обозначают
Видим, что всего данных чисел 44 = 256.Данный пример является иллюстрацией к следующему понятию, которое является частным случаем, когда наше основное множество состоит из различных элементов:Размещения с повторениями из n не обязательно различных элементов основного множества по n принято называть перестановками с повторениями. Число перестановок с повторениями обозначают  .Заметим,
.Заметим,  . Общее число перестановок с повторениями из n элементов равно
. Общее число перестановок с повторениями из n элементов равно 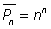 .В примере 2:
.В примере 2: 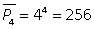 . Пример 3. Сколько семизначных чисел можно составить из 7 цифр: 1; 1; 2; 2; 2; 3; 4? Решение. Заметим, что «1» повторяется 2 раза, «3» — три раза, а «3» и «4» — по одному. На этот случай существует другая формула перестановок с повторениями.В общем случае, когда в нашем основном множестве какие-то элементы могут повторяться используют понятие:
. Пример 3. Сколько семизначных чисел можно составить из 7 цифр: 1; 1; 2; 2; 2; 3; 4? Решение. Заметим, что «1» повторяется 2 раза, «3» — три раза, а «3» и «4» — по одному. На этот случай существует другая формула перестановок с повторениями.В общем случае, когда в нашем основном множестве какие-то элементы могут повторяться используют понятие: Видим, что всего данных чисел 4·3·2 = 24.Данный пример является иллюстрацией к следующему понятию:
Видим, что всего данных чисел 4·3·2 = 24.Данный пример является иллюстрацией к следующему понятию: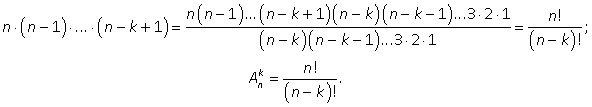
 Видим, что всего данных чисел 4 · 3 · 2 · 1 = 24.Данный пример является иллюстрацией к следующему понятию:Размещения из n элементов по n принято называть перестановками. Иначе, перестановки — это упорядоченные множества из n различных элементов основного множества по n. Перестановки отличаются друг от друга только порядком элементов. Число перестановок принято обозначать Рn. Общее число перестановок из n элементов равно Pn = n!.
Видим, что всего данных чисел 4 · 3 · 2 · 1 = 24.Данный пример является иллюстрацией к следующему понятию:Размещения из n элементов по n принято называть перестановками. Иначе, перестановки — это упорядоченные множества из n различных элементов основного множества по n. Перестановки отличаются друг от друга только порядком элементов. Число перестановок принято обозначать Рn. Общее число перестановок из n элементов равно Pn = n!. (1, 2, 3), (1, 2, 4), (1, 3, 4), (2, 3, 4).Видим, что всего получилось 4 подмножества.Данный пример является иллюстрацией к следующему понятию:
(1, 2, 3), (1, 2, 4), (1, 3, 4), (2, 3, 4).Видим, что всего получилось 4 подмножества.Данный пример является иллюстрацией к следующему понятию: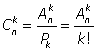 или
или 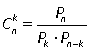 . Иначе
. Иначе  В примере 6:
В примере 6: 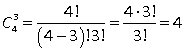 .
.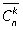 .
.  ,где n — количество необязательно различных элементов основного множества, k — количество выбираемых. Пример 8. Сколько будет костей в игре домино, если использовать, только четыре цифры 1, 2, 3, 4? Решение. Используем формулу сочетаний с повторениями:
,где n — количество необязательно различных элементов основного множества, k — количество выбираемых. Пример 8. Сколько будет костей в игре домино, если использовать, только четыре цифры 1, 2, 3, 4? Решение. Используем формулу сочетаний с повторениями:  Ответ:
Ответ: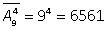 .Ответ:
.Ответ: способов.
способов.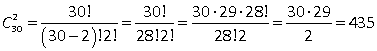 .
. вариантов.Ответ:
вариантов.Ответ: Например, (+ - +) означает, что горят 1-я и 3-я, (---) – не горит ни одна и т.д. в нашем случае у трехэлементного множества 23 = 8 подмножеств.
Например, (+ - +) означает, что горят 1-я и 3-я, (---) – не горит ни одна и т.д. в нашем случае у трехэлементного множества 23 = 8 подмножеств.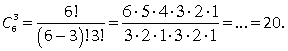 Ответ:
Ответ: .Ответ:
.Ответ: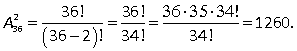 Ответ:
Ответ: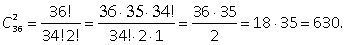
 дифференцируема в точке
дифференцируема в точке  , то есть приращение этой функции можно представить в виде суммы двух слагаемых: линейного относительно
, то есть приращение этой функции можно представить в виде суммы двух слагаемых: линейного относительно 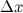 и нелинейного членов:
и нелинейного членов:
 при
при 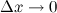 .
.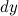 или
или 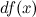 . Таким образом:
. Таким образом: