Определение 1. Наибольшим общим делителем (НОД)целых чисел a 1, a 2,…, an называется такое целое число D > 0, для которого выполняются два условия:
1) D – общий делитель чисел a 1, a 2,…, an, т.е. D делит каждое из этих чисел;
2) если d - общий делитель чисел a 1, a 2,…, an, то d | D.
Если все числа a 1, a 2,…, an равны нулю, то предполагается, что их НОД равен нулю.
Свойства наибольшего общего делителя.
10 Если НОД чисел a 1, a 2,…, an существует, то оно единственно.
20 НОД чисел a 1, a 2,…, an равно наибольшему из всех общих делителей этих чисел.
30 Для любых целых чисел a 1, a 2,…, an, b, q 1, q 2,…, qn
НОД (a 1, a 2,…, an, b) = НОД (a 1- bq 1, a 2- bq 2,…, an - bqn, b).
40 Для любых целых чисел a и b > 0, если b | a, то НОД (a, b) = b.
Наибольший общий делитель двух целых чисел a и b ¹ 0 вычисляется следующим способом:
Разделим число a на b с остатком:
 . (1)
. (1)
Если остаток r 1 = 0, то процесс заканчиваем (по свойству 40 НОД (a, b) = b). В противном случае разделим b на r 1 с остатком:
 . (2)
. (2)
Если остаток r 2 = 0, то процесс заканчиваем. В противном случае разделим r 1 на r 2 с остатком:
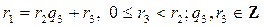 . (3)
. (3)
Если остаток r 3 = 0, то процесс заканчиваем. В противном случае разделим r 2 на r 3 с остатком и т.д. Процесс получения указанных равенств называется алгоритмом последовательного с остатком или алгоритмом Евклида.
На k -м шаге алгоритма Евклида получается равенство вида:
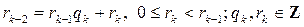 . (4)
. (4)
Покажем, что процесс всегда закончится. Допустим, что процесс последовательного деления с остатком никогда не закончится. Тогда получим бесконечную последовательность неравенств вида (1),(2), …, (4) получаем:
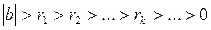 .
.
Откуда следует, что между числами | b | и 0 содержится бесконечно много целых чисел. Получаем противоречие с тем, что между любыми целыми числами содержится конечное число целых чисел. Следовательно, на некотором шаге должен получиться нулевой остаток и последовательность равенств вида (4) оборвется. Пусть в нашем случае последовательность равенств оборвется на k +1 шаге, где получим
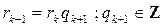 . (5)
. (5)
Тогда из последовательности равенств (1),(2), …, (4), (5) по свойствам 30, 40 получаем:
НОД(a, b) = НОД(b, r 1) = НОД(r 1, r 2) = …= НОД(rk -1, rk) = rk.
Таким образом, доказали теорему.
Теорема 1. Для любых целых чисел a, b ¹ 0 НОД существует, единственен и равен последнему отличному от нуля остатку в алгоритме Евклида, примененного к числам a, b. ÿ
Пример 1. Найти НОД чисел a = 2346, b = 1456. Применим к данным числам алгоритм Евклида:
2346 = 1456·1+890,
1456 = 890·1 + 566,
890 = 566·1 + 324,
566 = 324·1 + 242,
324 = 242·1 + 82,
242 = 82·2 + 78,
82 = 78·1 + 4,
78 = 4·19 +2,
4 = 2·2.
Таким образом, НОД(a, b) = 2.
НОД D чисел a 1, a 2,…, an находится по схеме
D 2=НОД(a 1, a 2), D 3=НОД(D 1, a 3),…, D = Dn =НОД(Dn- 1, an).
Теорема 2. Для любых целых чисел a 1, a 2,…, an D = НОД (a 1, a 2,…, an) представляется в виде:
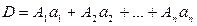 , (6)
, (6)
где A 1, A 2,…, An – целые числа.
Доказательство. Если все числа a 1, a 2,…, an равны нулю, то равенство (6) очевидно. Пусть теперь, не все из этих чисел равны нулю, например, a 1¹ 0. Рассмотрим множество
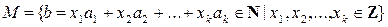 .
.
Множество M ¹Æ, так как число 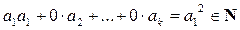 . Тогда по принципу минимума во множестве M есть наименьшее число; обозначим его через D:
. Тогда по принципу минимума во множестве M есть наименьшее число; обозначим его через D:
 . (7)
. (7)
Покажем, что D НОД чисел a 1, a 2,…, an.
Покажем, что D ОД чисел a 1, a 2,…, an. Допустим противное, что не все из этих чисел делятся на D, например, a 1 не делится на D. Разделим тогда a 1 на D с остатком: a 1 = Dq + r, 0< r < D. Тогда отсюда и из равенства (7) получаем
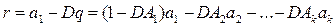 ,
,
т.е. число r < D принадлежит множеству M. Последнее утверждение противоречит выбору D. Таким образом, D ОД чисел a 1, a 2,…, an.
Далее из формулы (2) следует, что любой общий делитель d чисел a 1, a 2,…, an делит D. По определению D НОД чисел a 1, a 2,…, an. ÿ
Линейное представление НОД двух чисел можно найти по алгоритму Евклида из цепочки равенств (1), (2),…,(4):
 ,
,
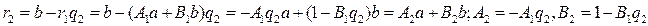 ,
,
Продолжая этот процесс, на последнем шаге мы получим линейное представление НОД чисел a и b.
 .
.
Пример 2. Найти линейное представление НОД чисел a = 2346, b = 1456. Используя равенства, полученные в примере 1, получаем:
890 = 2346 - 1456·1 = a - b,
566 = 1456 - 890·1 = b – (a - b) = 2 b - a,
324 = 890 - 566·1 = (a - b) – (2 b - a) = 2 a - 3 b,
242 = 566 - 324·1 = (2 b - a) – (2 a - 3 b) = 5 b - 3 a,
82 = 324 - 242·1 = (2 a - 3 b) – (5 b - 3 a) = 5 a - 8 b,
78 = 242 - 82·2 = (5 b - 3 a) – 2(5 a - 8 b) = 21 b - 13 a,
4 = 82 - 78·1 = (5 a - 8 b) – (21 b - 13 a) = 18 a - 29 b,
2 = 78 - 4·19 = (21 b - 13 a) – 19(18 a - 29 b) = 572 b - 355 a.
Таким образом, НОД(a, b) = 2 = 572 b - 355 a.
Определение 2. Целые числа a 1, a 2,…, an называются взаимно простыми, если их наибольший общий делитель равен 1. Обозначаем взаимную простоту чисел a 1, a 2,…, an символом (a 1, a 2,…, an) = 1.
Из теоремы 2 и определения 1 получаем теорему.
Теорема 3. Целые числа a 1, a 2,…, an взаимно простые тогда и только тогда, существуют такие целые числа A 1, A 2,…, An, что
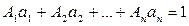 . ÿ (8)
. ÿ (8)
Из теоремы 3 легко доказать следующие свойства взаимно простых чисел.
10. Если a | bc и (a, b) = 1, то a | c.
20. Если a | c, b | c и (a, b) = 1, то ab | c.
30. (a, b 1 b 2… bm) = 1 тогда и только тогда, когда (a, bi) = 1 для всех i = 1,…, m.
40. Если НОД(a 1, a 2,…, an) = D, то числа a 1/ D, a 2/ D,…, an / D взаимно простые.
Определение 3. Наименьшим общим кратным (НОК) целых чисел a 1, a 2,…, an называется такое целое число m > 0, для которого выполняются два условия:
1) m – общее кратное чисел a 1, a 2,…, an, т.е. m делится на каждое из этих чисел;
2) если M - общее кратное чисел a 1, a 2,…, an, то m | M.
НОК двух чисел можно вычислить по следующей теореме.
Теорема 4. Для любых целых чисел a ¹ 0, b ¹ 0 НОК существует, единственно и вычисляется по формуле:

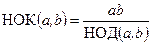 . (9)
. (9)
Пример 3. Найти НОД чисел a = 2346, b = 1456. Используя вычисления примера 1 по формуле 9 получаем:
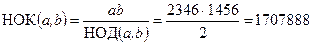 .
.



 . (1)
. (1) . (2)
. (2)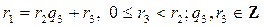 . (3)
. (3)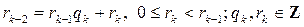 . (4)
. (4)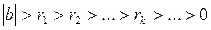 .
.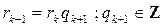 . (5)
. (5)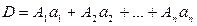 , (6)
, (6)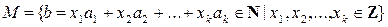 .
.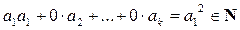 . Тогда по принципу минимума во множестве M есть наименьшее число; обозначим его через D:
. Тогда по принципу минимума во множестве M есть наименьшее число; обозначим его через D: . (7)
. (7)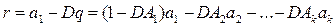 ,
, ,
,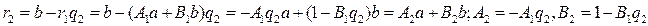 ,
, .
.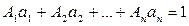 . ÿ (8)
. ÿ (8)
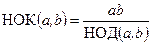 . (9)
. (9)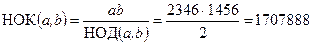 .
.


